-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2018; 8(1): 1-14
doi:10.5923/j.ajcam.20180801.01

Compromise Solutions for Fuzzy Multi-Level Multiple Objective Decision Making Problems
Tarek H. M. Abou-El-Enien1, Shereen Fathy El-Feky2
1Department of Operations Research & Decision Support, Faculty of Computers & Information, Cairo University, Giza, Egypt
2Teaching Assistant at Faculty of Computer Science, Department of Computer Science, Modern Science and Arts University, Giza, Egypt
Correspondence to: Shereen Fathy El-Feky, Teaching Assistant at Faculty of Computer Science, Department of Computer Science, Modern Science and Arts University, Giza, Egypt.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper extended the concept of the technique for order preference by similarity to ideal solution (TOPSIS) to develop a methodology to find compromise solutions for the Multi-Level Multiple Objective Decision Making (MLMODM) Problems with fuzzy parameters in the objective functions and the right hand side of the constraints (FMLMODM) of mixed (Maximize/Minimize)-type. Anew interactive algorithm is presented for the proposed TOPSIS approach for solving these types of mathematical programming problems. Also, an illustrative numerical example is solved and compared the solution of proposed algorithm with the solution of Global Criterion (GC) method.
Keywords: Compromise Programming, Fuzzy Programming, TOPSIS method, Global Criterion method, Interactive Decision Making, Multiple Objective Programming, Multi-level Programming, and Fuzzy Parameters
Cite this paper: Tarek H. M. Abou-El-Enien, Shereen Fathy El-Feky, Compromise Solutions for Fuzzy Multi-Level Multiple Objective Decision Making Problems, American Journal of Computational and Applied Mathematics , Vol. 8 No. 1, 2018, pp. 1-14. doi: 10.5923/j.ajcam.20180801.01.
Article Outline
1. Introduction
- Compromise programming (CP) was initially proposed by Zeleny (1973) and subsequently used by many researchers. [24]. Yu (1973) and Zeleny (1974) define the ideal solution (Yu describes this solution as the "utopia point") as any solution that would simultaneously optimize each individual objective. CP assumes that any DM seeks a solution as close as possible to the ideal point, [21, 25].The non-centralized planning has been recognized as an important decision making problem. It searches for a simultaneous compromise among the various objectives of the different departments. Multi-Level programming, a tool for modeling non-centralized decisions, consists of the objective(s) of the Manager at its first level and that is of the followers at the other levels. The decision-maker at each level seeks to optimize his individual objective Functions, which depends in part on the variables controlled by the decision makers at the other levels and their final decisions are executed sequentially where the upper-level decision-maker makes his decision firstly, [5, 7, 8, 11, 12, 16, 20].An extended TOPSIS method for solving interactive large scale multiple objective optimization problems involving fuzzy parameters is introduced in [4].Several algorithms for solving different kinds of large scale multiple objective optimization problems using TOPSIS approach are presented in [1].A review on theory, applications and softwares of bi-level, multi-level multiple criteria decision making and TOPSIS approach is presented in [2].Interactive TOPSIS algorithms for solving multi-level non-linear multi-objective decision-making problems are given in [6].A modified TOPSIS method for solving large scale two-level linear multiple objective optimization problems with fuzzy parameters in the right-hand side of the independent constraints is introduced in [3].We extend the TOPSIS method [4, 15] to find compromise solutions [14, 22, 25, 26, 27] for the Multi-Level Multiple Objective Decision Making (MLMODM) Problems with fuzzy parameters [18, 19, 23, 27] in the objective functions and the right hand side of the constraints (FMLMODM).In the following sections, the formulation of FMLMODM problems is given in section (2). By use of TOPSIS method, a new interactive algorithm for solving MLMODM problems is proposed in section (3). For the sake of illustration, we present an example for the extended TOPSIS method and compared the solution of proposed algorithm with the solution of traditional Global Criterion (GC) method in section (4).
2. Formulation of the Problem
- Consider the following FMLMODM problem:
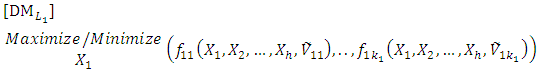 | (1-1) |
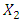 solves the
solves the  level
level 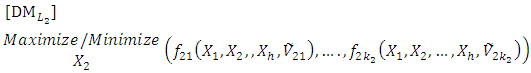 | (1-2) |
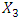 solves the
solves the  level
level 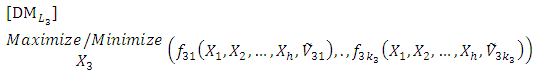 | (1-3) |
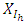 solves the
solves the 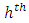 level
level 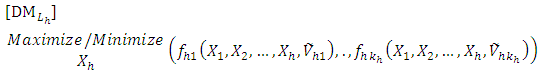 | (1-4) |
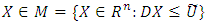 | (1-5) |
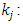 The number of objective functions of the
The number of objective functions of the 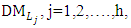
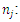 The number of variables of the
The number of variables of the 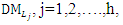
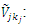 an n-dimensional row vector of fuzzy parameters for the
an n-dimensional row vector of fuzzy parameters for the 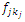 objective functions = 1,2,…,h.
objective functions = 1,2,…,h.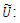 An m-dimensional column vector of right-hand sides of constraints whose elements are fuzzy Parameters
An m-dimensional column vector of right-hand sides of constraints whose elements are fuzzy Parameters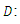 an
an 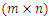 coefficient matrix,R: the set of all real numbers, X: an n-dimensional column vector of variables,Xj: an
coefficient matrix,R: the set of all real numbers, X: an n-dimensional column vector of variables,Xj: an 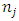 -dimensional column vector of variables for the jth level, j=1,2,…,h,
-dimensional column vector of variables for the jth level, j=1,2,…,h,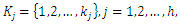
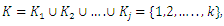
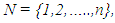
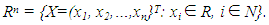 Throughout this paper, we assume that the column vectors of fuzzy parameters
Throughout this paper, we assume that the column vectors of fuzzy parameters 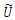 and
and 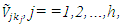 the row vectors of fuzzy parameters are characterized as the column vectors of fuzzy numbers and row vectors of fuzzy numbers respectively [18, 19, 23, 29]. It is appropriate to recall that a real fuzzy number
the row vectors of fuzzy parameters are characterized as the column vectors of fuzzy numbers and row vectors of fuzzy numbers respectively [18, 19, 23, 29]. It is appropriate to recall that a real fuzzy number 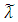 whose membership function
whose membership function 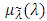 is defined as, [18, 19, 23, 29]:(1) A continuous mapping from R1 to the closed interval [0,1], (2)
is defined as, [18, 19, 23, 29]:(1) A continuous mapping from R1 to the closed interval [0,1], (2) 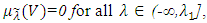 (3) Strictly increasing on
(3) Strictly increasing on 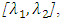 (4)
(4) 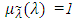 for all
for all 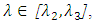 (5) Strictly decreasing on
(5) Strictly decreasing on 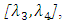 (6)
(6) 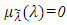 for all
for all 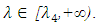 A possible shape of fuzzy number
A possible shape of fuzzy number 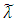 is illustrated in figure (1). The concept of α-cut of the vectors parameters
is illustrated in figure (1). The concept of α-cut of the vectors parameters 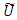 and
and 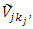
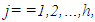 whose elements are fuzzy numbers is introduced as follows:
whose elements are fuzzy numbers is introduced as follows: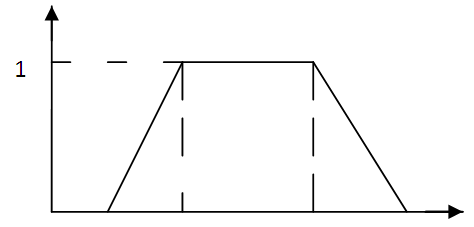 | Figure (1). Membership function of fuzzy number 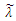 |
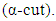 The α-cut of
The α-cut of 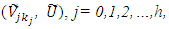 is defined as the ordinary set
is defined as the ordinary set 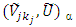 for which the degree of their membership function exceeds the level α є [0,1]:
for which the degree of their membership function exceeds the level α є [0,1]: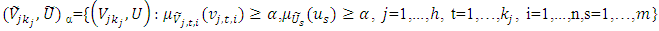 | (2) |
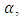 the FMLMODM problem (1) can be understood as the following nonfuzzy
the FMLMODM problem (1) can be understood as the following nonfuzzy 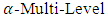 Multiple Objective Decision Making
Multiple Objective Decision Making 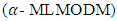 problem:
problem: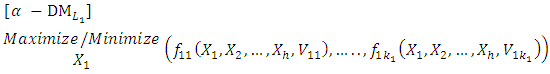 | (3-1) |
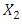 solves the
solves the 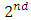 level
level 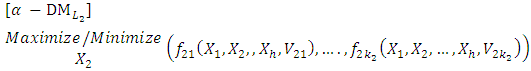 | (3-2) |
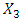 solves the
solves the  level
level 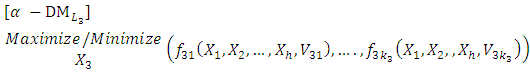 | (3-3) |
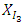 solves the
solves the 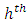 level
level 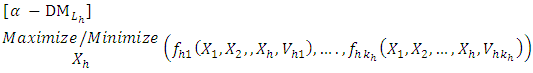 | (3-4) |
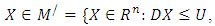 | (3-5) |
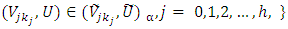 | (3-6) |
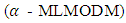 problem (3), the parameters
problem (3), the parameters 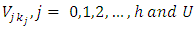 are treated as decision variables rather than constants.Based on the definition of α-cut of the fuzzy numbers, we characterize α–efficient solution of α- MLMODM problem (3):Definition 2:
are treated as decision variables rather than constants.Based on the definition of α-cut of the fuzzy numbers, we characterize α–efficient solution of α- MLMODM problem (3):Definition 2: 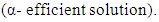 A solution
A solution 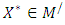 is said to be an α- efficient solution to the α- MLMODM problem (4), if and only if there does not exist another
is said to be an α- efficient solution to the α- MLMODM problem (4), if and only if there does not exist another 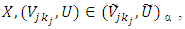
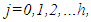 such that
such that 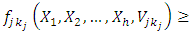
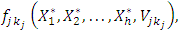
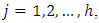 for maximizati
for maximizati 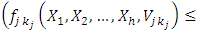
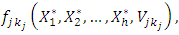
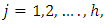 for minimization) and with strictly inequality holding for at least one
for minimization) and with strictly inequality holding for at least one 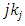 where the corresponding value of the parameter
where the corresponding value of the parameter 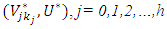 is called α-cut optimal parameters. Thus, the α-MLMODM problem (3) can be written as follows:
is called α-cut optimal parameters. Thus, the α-MLMODM problem (3) can be written as follows: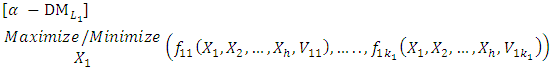 | (4-1) |
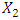 solves the
solves the 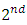 level
level 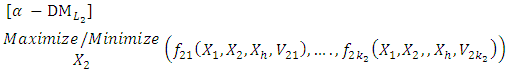 | (4-2) |
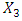 solves the
solves the 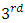 level
level 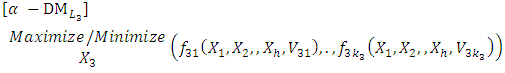 | (4-3) |
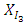 solves the
solves the 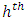 level
level 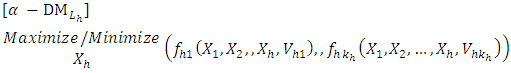 | (4-4) |
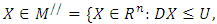 | (4-5) |
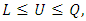 | (4-6) |
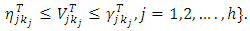 | (4-7) |
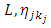 and
and 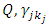 are lower and upper bound on
are lower and upper bound on 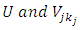 respectively.
respectively.3. TOPSIS for FMLMODEMs
- A modified version of TOPSIS method is introduced to find compromise solutions for the FMLMODM problems. Modified equations for the distance function [17] from the positive ideal solution (PIS) and the distance function from the negative ideal solution (NIS) are introduced to include all the objective functions of multi-level of the problem. An interactive decision making algorithm to find a compromise solution through TOPSIS approach is provided in (3-1) where the first level decision maker
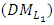 is asked to specify the membership function for each fuzzy parameter, the maximum negative and positive tolerance values, the power p of the distance functions, the degree α and the relative importance of the objectives. Then, the jth Level decision maker
is asked to specify the membership function for each fuzzy parameter, the maximum negative and positive tolerance values, the power p of the distance functions, the degree α and the relative importance of the objectives. Then, the jth Level decision maker 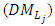 is asked to specify the maximum negative and positive tolerance values, and the relative importance of the objectives. An illustrative numerical example for the extended TOPSIS method is given in section (4).In order to obtain a compromise solutions to the FMLMODM problems using the modified TOPSIS approach, a generalized formulas for the distance function from the PIS and the distance function from the NIS are proposed and modeled to include all the objective functions of all the levels. Thus, we propose an interactive decision making algorithm to find a compromise solutions through TOPSIS approach where the
is asked to specify the maximum negative and positive tolerance values, and the relative importance of the objectives. An illustrative numerical example for the extended TOPSIS method is given in section (4).In order to obtain a compromise solutions to the FMLMODM problems using the modified TOPSIS approach, a generalized formulas for the distance function from the PIS and the distance function from the NIS are proposed and modeled to include all the objective functions of all the levels. Thus, we propose an interactive decision making algorithm to find a compromise solutions through TOPSIS approach where the 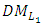 is asked to specify the membership function for each fuzzy parameter, the maximum negative and positive tolerance values, the power p of the distance functions, the degree α and the relative importance of the objectives. Then, the
is asked to specify the membership function for each fuzzy parameter, the maximum negative and positive tolerance values, the power p of the distance functions, the degree α and the relative importance of the objectives. Then, the 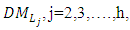 is asked to specify the maximum negative and positive tolerance values, and the relative importance of the objectives.Algorithm (I):Phase (1):Step 1:(!-1): Let h = the number of the levels of the FMLMODM problem (1). Set j=1, "The 1st level".(1-2): Ask the
is asked to specify the maximum negative and positive tolerance values, and the relative importance of the objectives.Algorithm (I):Phase (1):Step 1:(!-1): Let h = the number of the levels of the FMLMODM problem (1). Set j=1, "The 1st level".(1-2): Ask the 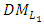 to specify a membership function for each fuzzy numbers
to specify a membership function for each fuzzy numbers 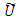 and
and 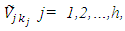 in the FMLMODM problem (1).For example, the fuzzy numbers
in the FMLMODM problem (1).For example, the fuzzy numbers 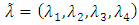 can have a membership function of the following form [13]:
can have a membership function of the following form [13]: 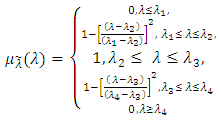 | (5) |
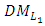 to select
to select  (1-4): Transform the FMLMODM problem (1) to the form of α-MLMODM problem (4) by using steps (1-2) and (1-3). Step 2:Construct the PIS payoff table of the following problem:
(1-4): Transform the FMLMODM problem (1) to the form of α-MLMODM problem (4) by using steps (1-2) and (1-3). Step 2:Construct the PIS payoff table of the following problem: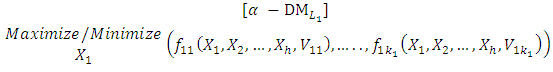 Subject to (6)
Subject to (6) 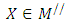 and obtain
and obtain 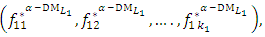 the individual positive ideal solutions.where
the individual positive ideal solutions.where 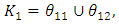
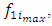 Objective Functions for Maximization,
Objective Functions for Maximization, 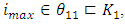 and
and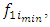 Objective Functions for Minimization,
Objective Functions for Minimization, 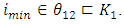 Step 3:Construct the NIS payoff table of problem (6) and obtain
Step 3:Construct the NIS payoff table of problem (6) and obtain 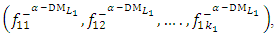 the individual negative ideal solutions. Step 4:Use steps (2 and 3) to construct the distance function from the PIS and the distance function from the NIS:
the individual negative ideal solutions. Step 4:Use steps (2 and 3) to construct the distance function from the PIS and the distance function from the NIS: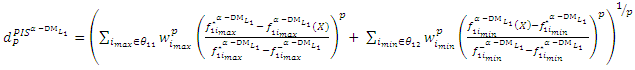 | (7-1) |
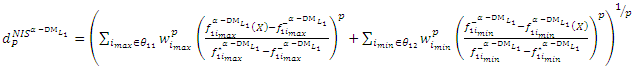 | (7-2) |
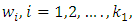 are the relative importance (weighs) of objectives, and
are the relative importance (weighs) of objectives, and 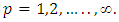 Step 5:Transfer the
Step 5:Transfer the 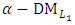 problem (6) into the following bi-objective problem with two commensurable (but often conflicting) objectives:
problem (6) into the following bi-objective problem with two commensurable (but often conflicting) objectives: 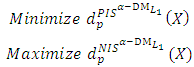 Subject to (8)
Subject to (8) 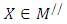 Where
Where 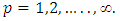 Step 6:(6-1): Ask the
Step 6:(6-1): Ask the 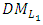 to select
to select 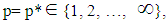 (6-2): Ask the
(6-2): Ask the 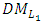 to select
to select 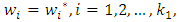 where
where 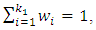 Step 7: Use step (6) and equation (7) to compute
Step 7: Use step (6) and equation (7) to compute 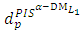 and
and 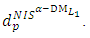 Step 8: Construct the payoff table of problem (8) and obtain:
Step 8: Construct the payoff table of problem (8) and obtain: 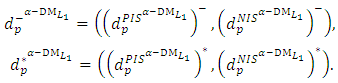 Step 9:(9-1): Construct the following membership functions
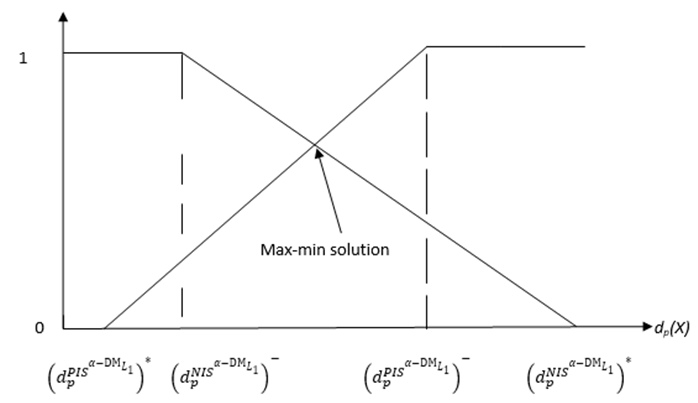
Step 9:(9-1): Construct the following membership functions 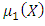 and
and 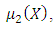 (figure (2)):
(figure (2)):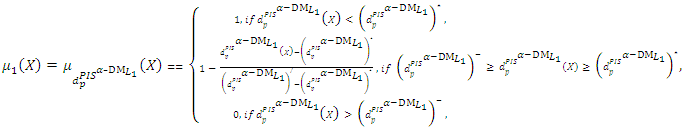 | (9-1) |
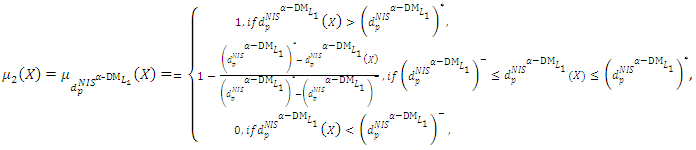 | (9-2) |
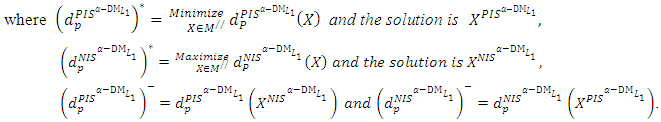 (9-2): By using the max-min decision model, [9], the Tchebycheff model, [10], and the membership functions (9), construct the following satisfactory level model:
(9-2): By using the max-min decision model, [9], the Tchebycheff model, [10], and the membership functions (9), construct the following satisfactory level model: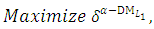 | (10-1) |
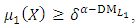 | (10-2) |
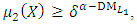 | (10-3) |
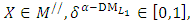 | (10-4) |
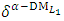 is the satisfactory level for both criteria of the shortest distance from the PIS and the farthest distance from the NIS. (9-3): Solve problem (10) to obtain the Pareto optimal solution
is the satisfactory level for both criteria of the shortest distance from the PIS and the farthest distance from the NIS. (9-3): Solve problem (10) to obtain the Pareto optimal solution 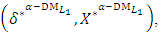 then
then 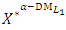 is a nondominated solution of (8) and a compromise solution of the
is a nondominated solution of (8) and a compromise solution of the 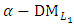 problem (6).(9-4): If the
problem (6).(9-4): If the 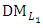 is satisfied with
is satisfied with 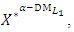 then go to step (10). Otherwise, go to step (6-2). Step 10:(10-1): Ask the
then go to step (10). Otherwise, go to step (6-2). Step 10:(10-1): Ask the 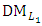 to select the maximum acceptable negative and positive tolerance (relaxation) values, [18, 20],
to select the maximum acceptable negative and positive tolerance (relaxation) values, [18, 20], 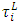 and
and 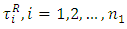 on the decision vector,
on the decision vector, 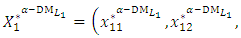
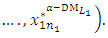 (10-2): Construct the linear membership functions (Figure 3) for each of the
(10-2): Construct the linear membership functions (Figure 3) for each of the 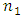 components of the decision vector
components of the decision vector 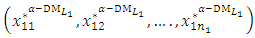 controlled by the
controlled by the 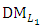 can be formulated as:
can be formulated as: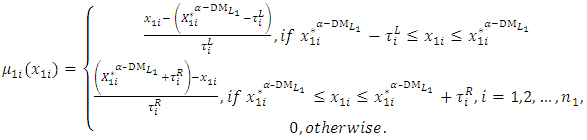 | (11) |
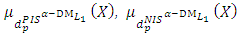
 | Figure (2). The membership functions of 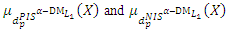 |
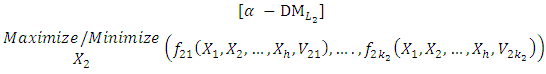 Subject to (12)
Subject to (12) 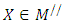 and obtain
and obtain 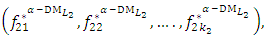 the individual positive ideal solutions.where
the individual positive ideal solutions.where 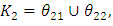
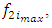 Objective Functions for Maximization,
Objective Functions for Maximization, 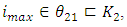 and
and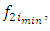 Objective Functions for Minimization,
Objective Functions for Minimization, 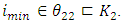 Step 12:Construct the NIS payoff table of problem (12) and obtain
Step 12:Construct the NIS payoff table of problem (12) and obtain 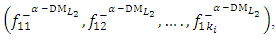 theindividual negative ideal solutions. Step 13:Use steps (11 and 12) to construct the distance function from the PIS and the distance function from the NIS:
theindividual negative ideal solutions. Step 13:Use steps (11 and 12) to construct the distance function from the PIS and the distance function from the NIS: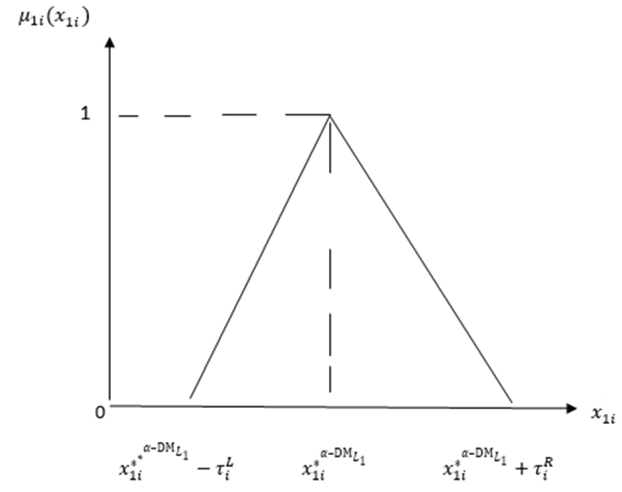 | Figure (3). The membership function of the decision variable 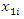 |
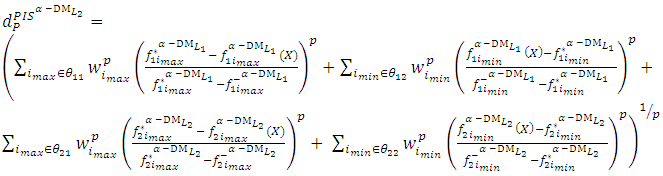 | (13-1) |
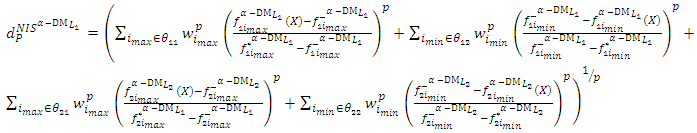 | (13-2) |
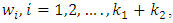 are the relative importance (weighs) of objectives, and
are the relative importance (weighs) of objectives, and 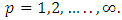 Step 14:Transfer the
Step 14:Transfer the 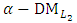 problem (12) into the following bi-objective problem with two commensurable (but often conflicting) objectives:
problem (12) into the following bi-objective problem with two commensurable (but often conflicting) objectives: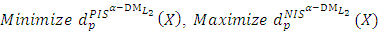 Subject to (14)
Subject to (14)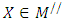 where
where 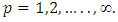 Step 15:(15-1): Ask the
Step 15:(15-1): Ask the 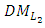 to select
to select 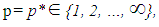 (15-2): Ask the
(15-2): Ask the 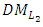 to select
to select 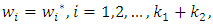 where
where 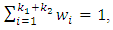 Step 16: Use step (12) and equation (13) to compute
Step 16: Use step (12) and equation (13) to compute 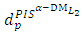 and
and 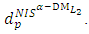 Step 17: Construct the payoff table of problem (14) and obtain:
Step 17: Construct the payoff table of problem (14) and obtain: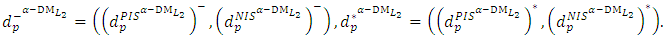 Step 18:(18-1): Construct the following membership functions
Step 18:(18-1): Construct the following membership functions 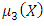 and
and 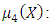
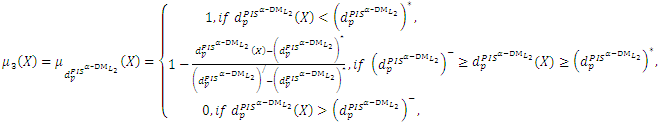 | (15-1) |
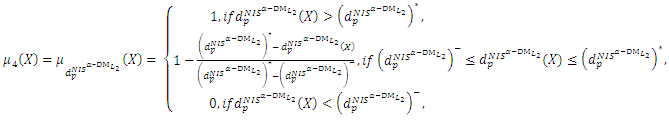 | (15-2) |
 (18-2): By using the max-min decision model [9], the Tchebycheff model, [10], and the membership functions (15), construct the following satisfactory level model:
(18-2): By using the max-min decision model [9], the Tchebycheff model, [10], and the membership functions (15), construct the following satisfactory level model: | (16-1) |
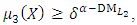 | (16-2) |
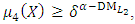 | (16-3) |
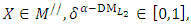 | (16-4) |
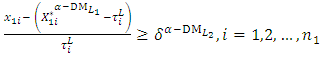 | (16-5) |
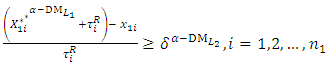 | (16-6) |
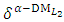 is the satisfactory level for both criteria of the shortest distance from the PIS and the farthest distance from the NIS.(18-3): Solve problem (16) to obtain the Pareto optimal solution
is the satisfactory level for both criteria of the shortest distance from the PIS and the farthest distance from the NIS.(18-3): Solve problem (16) to obtain the Pareto optimal solution 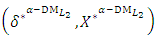 , then
, then 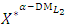 is a non-dominated solution of (14) and a compromise solution of the
is a non-dominated solution of (14) and a compromise solution of the 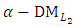 problem (12).(18-4): If the
problem (12).(18-4): If the 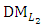 is satisfied with
is satisfied with 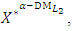 then go to step (19). Otherwise, go to step (15-2).Step 19: If h =j, stop. Otherwise, go to step (20).Step 20:(20-1): Ask the
then go to step (19). Otherwise, go to step (15-2).Step 19: If h =j, stop. Otherwise, go to step (20).Step 20:(20-1): Ask the 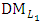 to select the maximum acceptable negative and positive tolerance (relaxation) values
to select the maximum acceptable negative and positive tolerance (relaxation) values 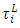 and
and 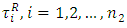 on the decision vector,
on the decision vector, 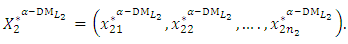 (20-2): Construct the linear membership functions for each of the
(20-2): Construct the linear membership functions for each of the 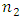 components of the decision vector
components of the decision vector 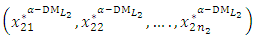 controlled by the
controlled by the 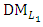 can be formulated as:
can be formulated as: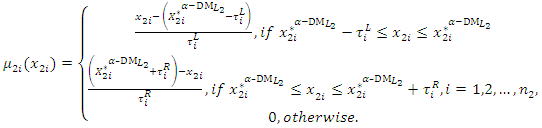 | (17) |
4. Illustrative Numerical Example for Algorithm (I)
- Consider the following FMLMODM problem:
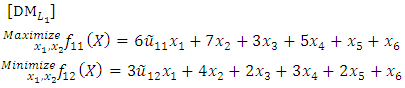 where
where 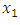 and
and 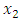 solves the second level
solves the second level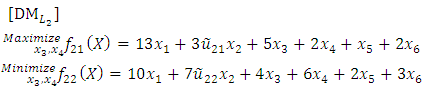 where
where 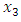 and
and 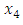 solves the third level
solves the third level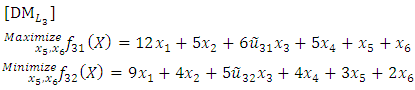 Subject to
Subject to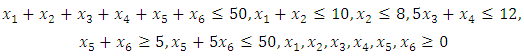 where
where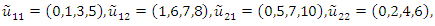
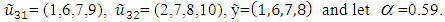 Use the introduced algorithm in subsection (3-1) to solve the above problem.Solution:- h= 3, j=1,- Use the membership function (5) to convert the above problem to the following α-MLMODM problem,
Use the introduced algorithm in subsection (3-1) to solve the above problem.Solution:- h= 3, j=1,- Use the membership function (5) to convert the above problem to the following α-MLMODM problem,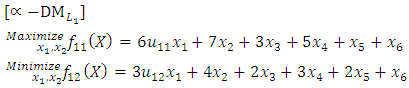 where
where 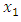 and
and 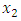 solves the second level
solves the second level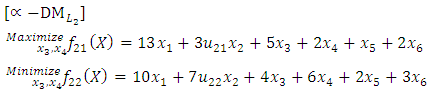 where
where 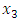 and
and 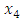 solves the third level
solves the third level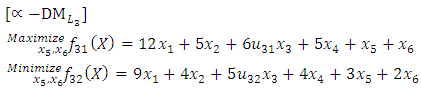 Subject to
Subject to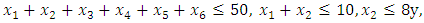
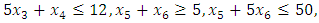
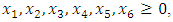
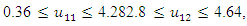
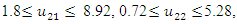
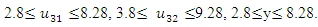 - Obtain PIS and NIS payoff tables for the
- Obtain PIS and NIS payoff tables for the 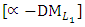 of the Problem:
of the Problem: | Table (1). PIS payoff table for 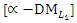 the problem the problem |
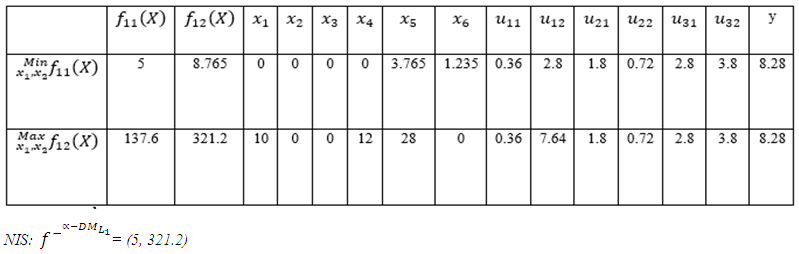 | Table (2). NIS payoff table for 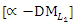 the problem the problem |
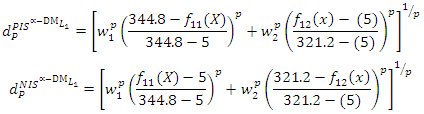 - Thus, problem is obtained. In order to get numerical solutions, assume that
- Thus, problem is obtained. In order to get numerical solutions, assume that 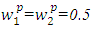 and p=2,
and p=2,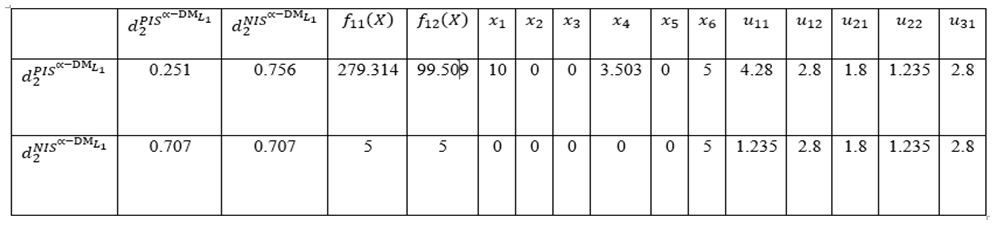 | Table (3). PIS payoff table of problem 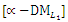 when p=2 when p=2 |
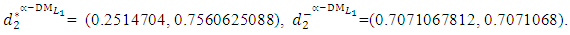 - Now, it is easy to compute problem (15):
- Now, it is easy to compute problem (15):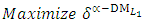 Subject to
Subject to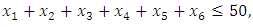
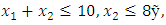
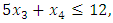
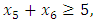
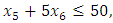
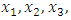
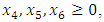
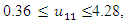
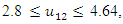
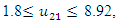
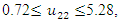
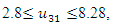
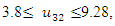
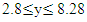
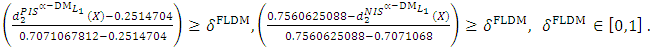 - The maximum “satisfactory level”
- The maximum “satisfactory level” 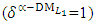 is achieved for the solution
is achieved for the solution 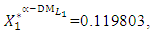
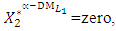
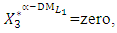
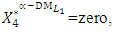
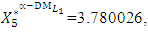
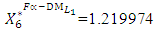 - Let the
- Let the 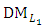 decide
decide 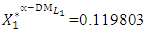 with positive tolerance
with positive tolerance 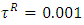 and
and 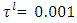 and
and 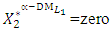 with positive tolerance
with positive tolerance 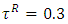 and
and 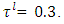 - j=2. Obtain PIS and NIS payoff tables for the
- j=2. Obtain PIS and NIS payoff tables for the 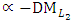 Problem.
Problem. | Table (4). PISpayoff table for the 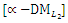 problem problem |
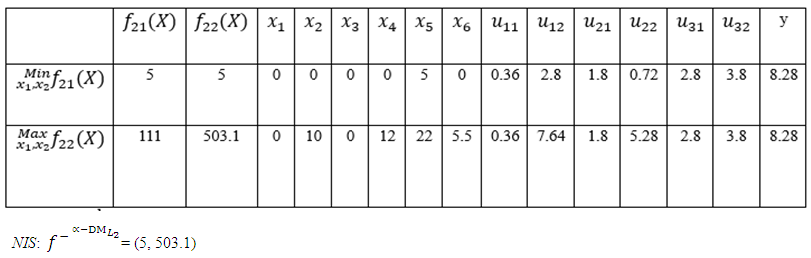 | Table (5). NIS payoff table for the  problem problem |
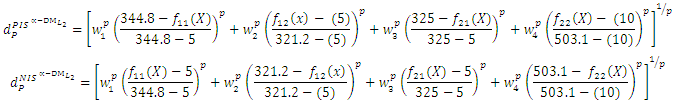 - Thus, problem is obtained. In order to get numerical solutions, assume that
- Thus, problem is obtained. In order to get numerical solutions, assume that 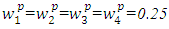 and p=2,
and p=2, | Table (6). PIS payoff table of problem 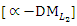 when p=2 when p=2 |
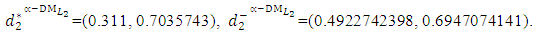 - Now, it is easy to compute:
- Now, it is easy to compute: 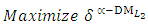 subject to
subject to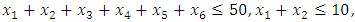
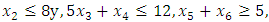
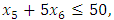
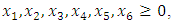
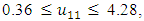
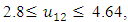
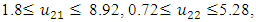
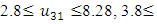
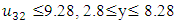
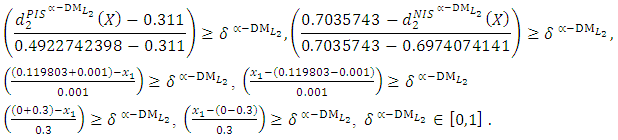 - The maximum “satisfactory level”
- The maximum “satisfactory level” 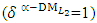 is achieved for the solution
is achieved for the solution 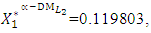
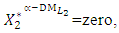
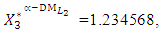
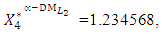
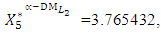
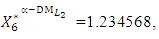 Let the
Let the 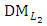 decide
decide 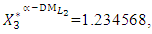
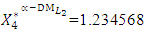 with positive tolerance
with positive tolerance 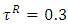 and
and 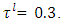 - j=3. Obtain PIS and NIS payoff tables for the
- j=3. Obtain PIS and NIS payoff tables for the 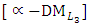 Problem:
Problem: | Table (7). PIS payoff table for the 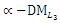 problem problem |
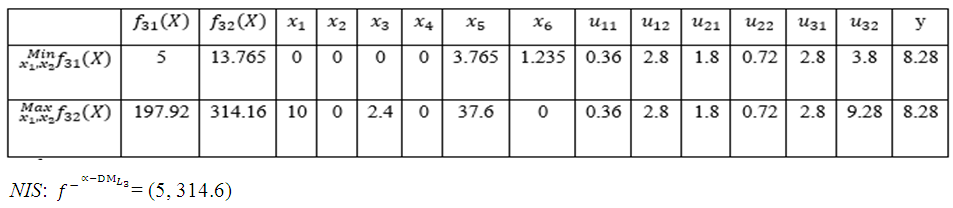 | Table (8). NIS payoff table for the  problem problem |
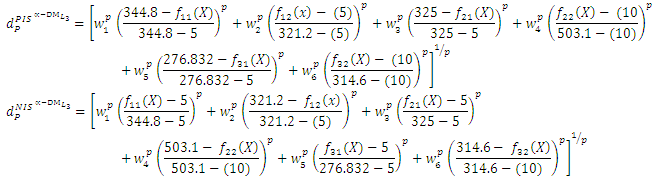 - Thus, problem is obtained. In order to get numerical solutions, assume that
- Thus, problem is obtained. In order to get numerical solutions, assume that 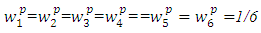 and p=2
and p=2 | Table (9). PIS payoff table of problem  when p=2 when p=2 |
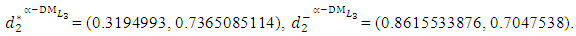 - Now, it is easy to compute:
- Now, it is easy to compute: 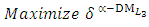 Subject to
Subject to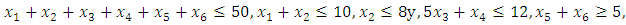
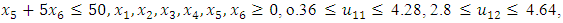
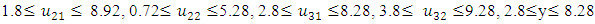
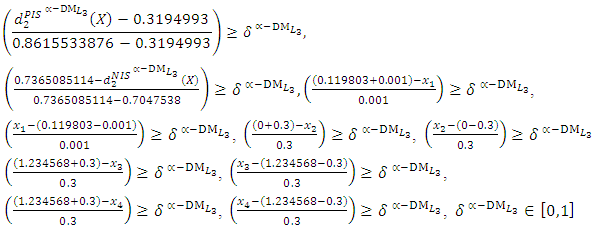 - The “satisfactory level”
- The “satisfactory level” 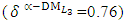 is achieved for the solution
is achieved for the solution 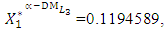
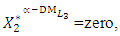
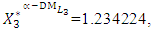
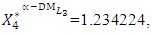
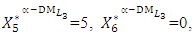 The comparison between the proposed TOPSIS method and the traditional GC method is given in Table (10). In general, the results show that the proposed interactive modified TOPSIS method is introducing better results than (or closer results to) the traditional GC method.
The comparison between the proposed TOPSIS method and the traditional GC method is given in Table (10). In general, the results show that the proposed interactive modified TOPSIS method is introducing better results than (or closer results to) the traditional GC method.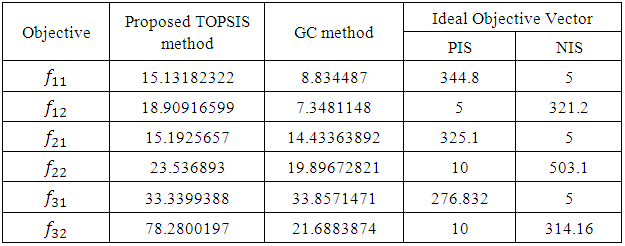 | Table (10) |
5. Conclusions
- This paper extended TOPSIS approach to find compromise solutions for the FMLMODM of mixed (Maximize/Minimize)-type. Anew interactive algorithm is presented for the proposed TOPSIS approach for solving these type of mathematical programming problems. Also, an illustrative numerical example is solved and compared the solution of proposed algorithm with the solution of the traditional GC method. In general, the results show that the proposed TOPSIS method is introducing better results than (or closer results to) the traditional GC method.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML