Ogunrinde R. B., Ayinde S. O.
Department of Mathematics, Faculty of Science, Ekiti State University, Ado Ekiti, Nigeria
Correspondence to: Ayinde S. O., Department of Mathematics, Faculty of Science, Ekiti State University, Ado Ekiti, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we present a new numerical integration of a derived interpolating function using the Gompertz Function approach for solving first order differential equations. The new numerical integration obtained was used to solve some oscillatory and exponential problems. The effectiveness of the new Integrator was verified and the results obtained show that the Integrator is computational reliable and stable.
Keywords:
Numerical integration, Oscillatory and exponential problems, Gompertz Function, Interpolating Function
Cite this paper: Ogunrinde R. B., Ayinde S. O., A Numerical Integration for Solving First Order Differential Equations Using Gompertz Function Approach, American Journal of Computational and Applied Mathematics , Vol. 7 No. 6, 2017, pp. 143-148. doi: 10.5923/j.ajcam.20170706.01.
1. Introduction
Differential equations are used to model problems in science and engineering that involve the change of some variables with respect to another. Most of these problems required the solution of an initial value problem. Many scholars [1, 3, 5] have approached the problems in various ways by formulating an interpolating function through which an integration scheme which is particularly well suited were developed and used to solve the problems. Similarly, Mathematician scholars have approached the growth problems by formulating functions and distributions which play an important role in modeling survival times, human mortality and actuarial data. [2, 4]Gompertz proposed and showed that if the average exhaustions of a man’s power to avoid death were such that at the end of equal infinitely small intervals of time, he lost equal portions of his remaining power to oppose destruction. The number of survivors was given by the equation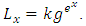 | (1) |
Winsor in 1932 for more convenient was written in the form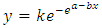 | (2) |
in which k and b are essentially positive quantities.The Gompertz curve or function which has been useful for the empirical representation of growth phenomena. These functions have for long been applied to Actuarial and Demographic problems such as: growth of organisms, psychological growth and population growth. In this research, we consider an interpolating function in similitude to Gompertz function with additional terms added and derived a numerical integration that can compete favorably in solving some physical problems of growth phenomena, the two parameters (Scale and shape) were considered in the formulation. Therefore, we formulate or derived new computational numerical integration scheme from the method based on the theoretical solution  to the initial value problem of the form:
to the initial value problem of the form: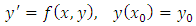 | (3) |
in the interval 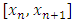 by considering the interpolating function
by considering the interpolating function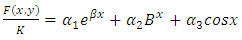 | (4) |
Where 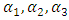 are real undetermined coefficients,
are real undetermined coefficients, 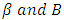 are the shape and scale parameters, K represent the saturation level using Gompertz approach. The intervals defined are
are the shape and scale parameters, K represent the saturation level using Gompertz approach. The intervals defined are 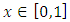 and
and 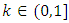 . Some conditions will be imposed on (4) to guarantee the derivation of the method. The numerical experiments will be carried out on some initial value problems and the test results show the reliability of the method.
. Some conditions will be imposed on (4) to guarantee the derivation of the method. The numerical experiments will be carried out on some initial value problems and the test results show the reliability of the method.
2. Derivation of the Integrator
We can assume that the theoretical solution 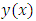 to the initial value problem (3) can be locally represented in the interval
to the initial value problem (3) can be locally represented in the interval 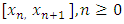 by the non-polynomial interpolating function (4) above, that is
by the non-polynomial interpolating function (4) above, that is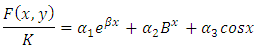 We shall assume
We shall assume 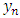 is a numerical estimate to the theoretical solution
is a numerical estimate to the theoretical solution 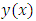 and
and 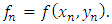 We define mesh points as follows:
We define mesh points as follows: 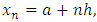 and
and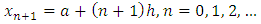 | (5) |
We can impose the following constraints on the interpolating function (4) in order to get the undetermined coefficients.
2.1. Constraints
a. The interpolating function must coincide with the theoretical solution at 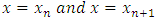 . Hence we required that
. Hence we required that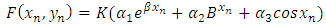 | (6) |
and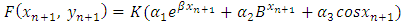 | (7) |
b. Secondly, the derivatives of the interpolating function are required to coincide with the differential equation as well as its first, second, and third derivatives with respect to 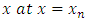 We denote the i-th total derivatives of
We denote the i-th total derivatives of  with respect to x with
with respect to x with  such that
such that 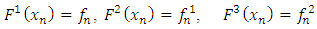 | (8) |
2.2. Derivation of the Numerical Integrator
Following from (8), we differentiate (4) to obtain 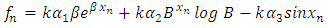 | (9) |
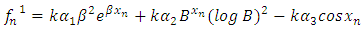 | (10) |
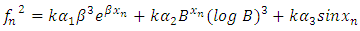 | (11) |
We formed a system of equation to solve for 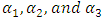 from (9) to (11),Hence we have,
from (9) to (11),Hence we have,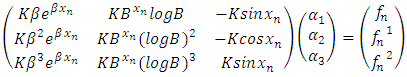 | (12) |
Taking this system of equation such as 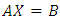 , using Cramer rule it gives
, using Cramer rule it gives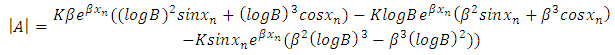 | (13) |
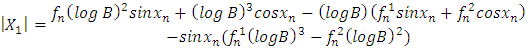 | (14) |
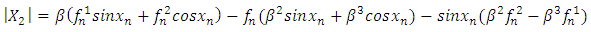 | (15) |
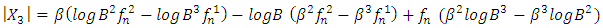 | (16) |
Therefore, we can deduce that 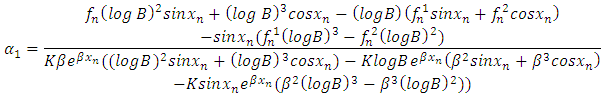 | (17) |
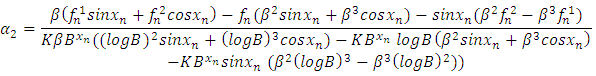 | (18) |
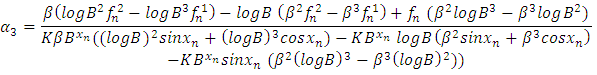 | (19) |
Since 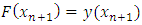 and
and 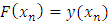 Implies that
Implies that 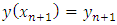 and
and 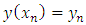 Then
Then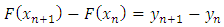 | (20) |
and therefore we shall have from putting (6) and (7) into (20), 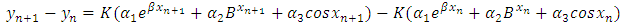 | (21) |
Simplifying (21) gives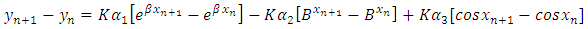 | (22) |
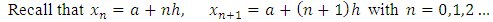 | (23) |
Therefore, by expansion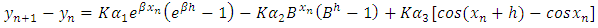 | (24) |
Hence, (24) can be written compactly as 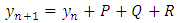 Where
Where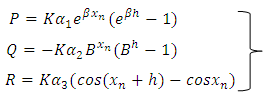 | (25) |
Substituting for 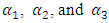 from (17, 18, 19) in (25), we have
from (17, 18, 19) in (25), we have 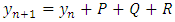 | (26) |
where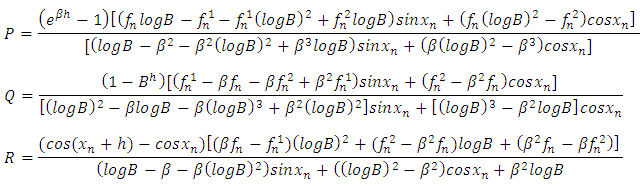 is the new numerical schemes for the solution of the first order differential equation.
is the new numerical schemes for the solution of the first order differential equation.
3. The Implementation of the Integrator
In this paper, however, we limit the numerical integration (26) to first test on some oscillatory and exponential problems of the first order differential equations so as to show the reliability and stability of the integration before applying it to solve the physical problems of growth phenomena.Example 1Using the Integrator (26) to solve the initial value problem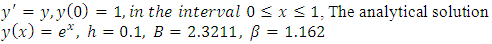
Table 1
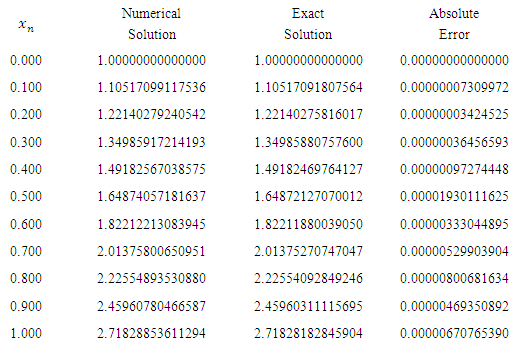 |
| |
|
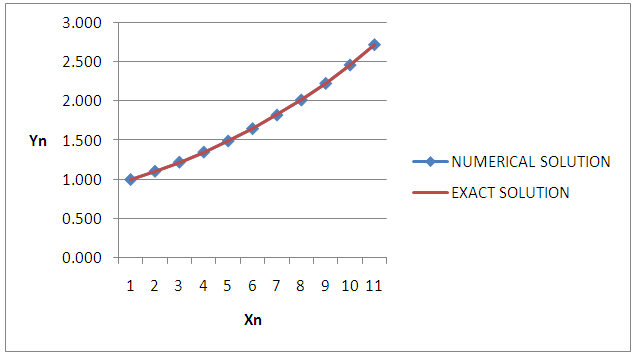 | Figure 1. The graph of the Numerical and Exact solution of 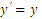 |
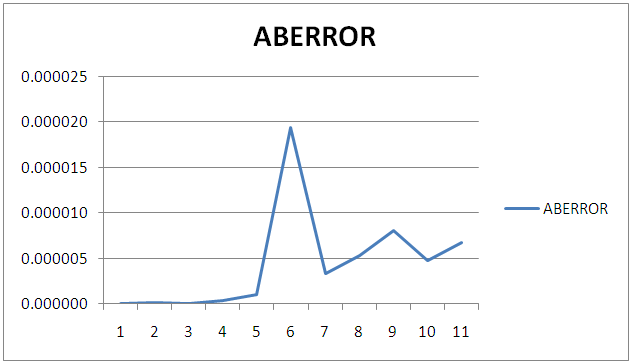 | Figure 2. The graph of the Absolute Error of Numerical and Exact solution of 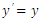 |
Example 2Using the Integrator (26) to solve the initial value problem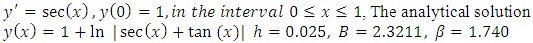
Table 2
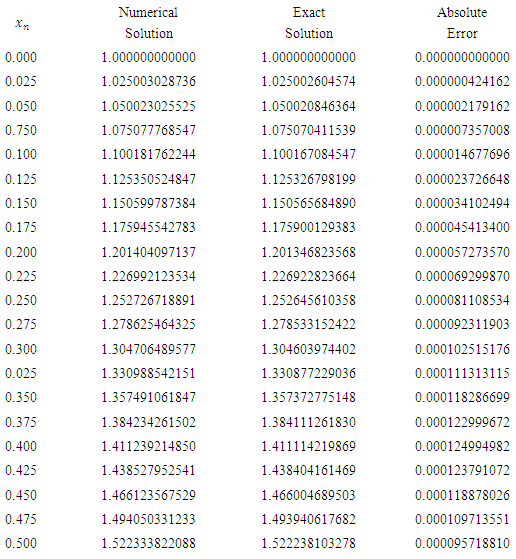 |
| |
|
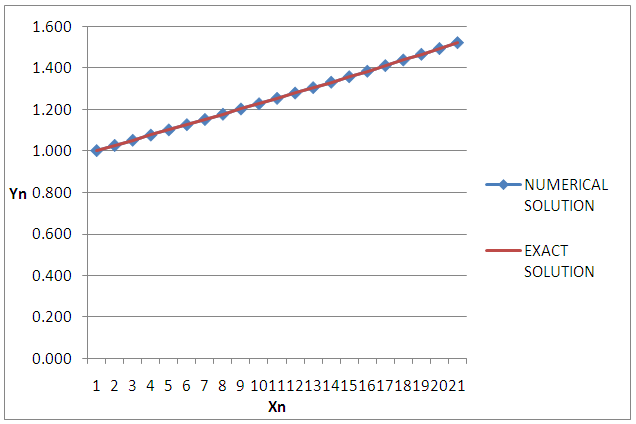 | Figure 3. The graph of the Numerical and Exact solution of 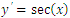 |
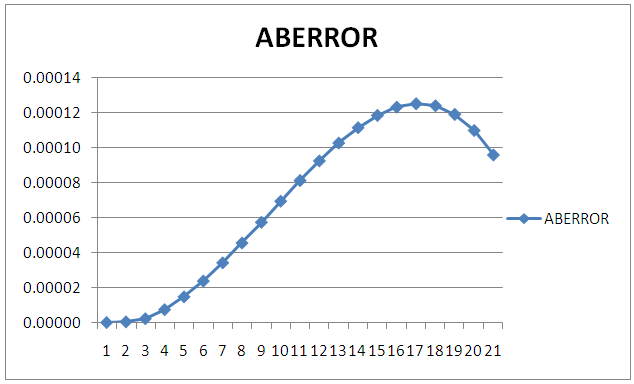 | Figure 4. The graph of the Absolute Error of Numerical and Exact solution of  |
4. Conclusions
In conclusion, we have presented a new numerical integration of a derived interpolating function using the Gompertz Function approach for solving first order differential equations. The interpolating function in comparison with Gompertz function with little modification was used, and the scale and the shape parameters were considered. The reliability of the new Integrator was verified and the results obtained show that the Integrator is computational reliable and stable, when the new numerical integration obtained was used to solve some oscillatory and exponential problems.However the Integrator will be used to solve growth and population problems in the next paper where Gompertz Function and the equation has been widely used.
References
| [1] | Ayinde, S. O. et al. (2015). “A New Numerical Method for solving First Order Differential Equations” American Journal of Applied Mathematics and Statistics. Vol. 3, No. 4, 156-160. |
| [2] | Charles, P. W. (1932). “The Gompertz Curve as a Growth Curve”. Proceedings of the National Academy of Sciences. Vol. 18, No 1. 1-8. |
| [3] | Fatunla, S. O. (1976). “A New Algorithm for Numerical Solution of ODEs”. Computer and Mathematics with Applications. Vol. 2, pp 247 – 253. |
| [4] | Gompertz, Benjamin (1825). “On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Method of Determining the value of Life Contingencies”. Phil. Transactions Royal Society. 513 – 585. |
| [5] | Ibijola E.A. et al (2010). “On a New Numerical Scheme for the Solution of Initial Value Problems in ODE”. Australian Journal of Basic and Applied Sciences. 4(10): 5277-5282. |



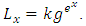
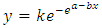
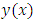 to the initial value problem of the form:
to the initial value problem of the form: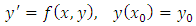
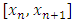 by considering the interpolating function
by considering the interpolating function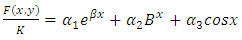
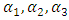 are real undetermined coefficients,
are real undetermined coefficients, 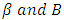 are the shape and scale parameters, K represent the saturation level using Gompertz approach. The intervals defined are
are the shape and scale parameters, K represent the saturation level using Gompertz approach. The intervals defined are 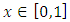 and
and 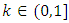 . Some conditions will be imposed on (4) to guarantee the derivation of the method. The numerical experiments will be carried out on some initial value problems and the test results show the reliability of the method.
. Some conditions will be imposed on (4) to guarantee the derivation of the method. The numerical experiments will be carried out on some initial value problems and the test results show the reliability of the method.  to the initial value problem (3) can be locally represented in the interval
to the initial value problem (3) can be locally represented in the interval  by the non-polynomial interpolating function (4) above, that is
by the non-polynomial interpolating function (4) above, that is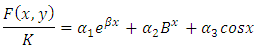 We shall assume
We shall assume 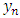 is a numerical estimate to the theoretical solution
is a numerical estimate to the theoretical solution 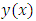 and
and 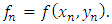 We define mesh points as follows:
We define mesh points as follows: 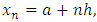 and
and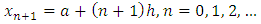
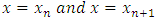 . Hence we required that
. Hence we required that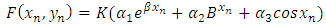
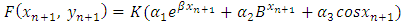
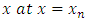 We denote the i-th total derivatives of
We denote the i-th total derivatives of 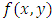 with respect to x with
with respect to x with 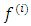 such that
such that 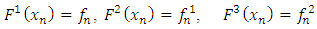
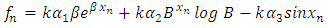
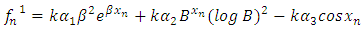
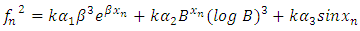
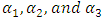 from (9) to (11),Hence we have,
from (9) to (11),Hence we have,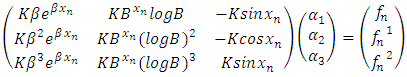
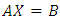 , using Cramer rule it gives
, using Cramer rule it gives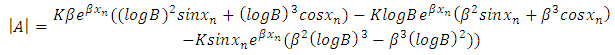
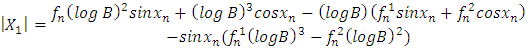
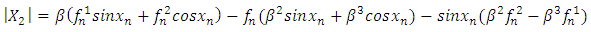
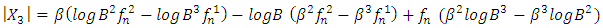
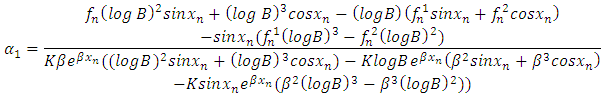
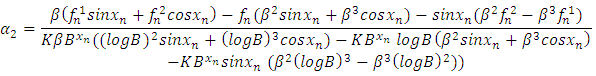
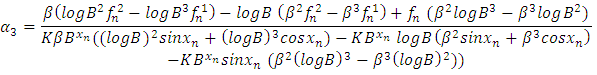
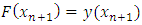 and
and 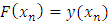 Implies that
Implies that 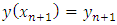 and
and 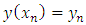 Then
Then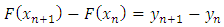
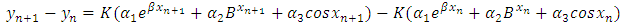
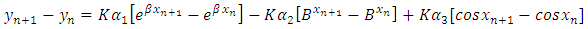
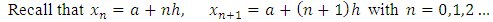
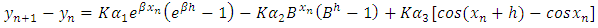
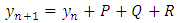 Where
Where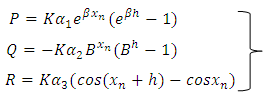
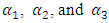 from (17, 18, 19) in (25), we have
from (17, 18, 19) in (25), we have 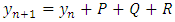
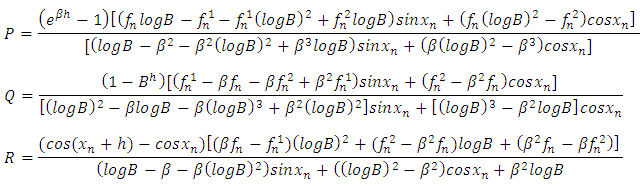 is the new numerical schemes for the solution of the first order differential equation.
is the new numerical schemes for the solution of the first order differential equation.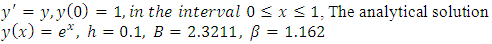

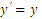

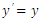
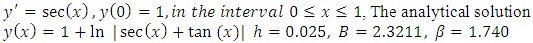

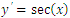


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
