-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2017; 7(5): 138-141
doi:10.5923/j.ajcam.20170705.03

On Using the Min-Function in Fuzzy Programming within the GAMS Software
Maged George Iskander
The British University in Egypt, Department of Business Administration, El Sherouk City, Cairo, Egypt
Correspondence to: Maged George Iskander , The British University in Egypt, Department of Business Administration, El Sherouk City, Cairo, Egypt.
| Email: |  |
Copyright © 2017 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Using the min-function is essential in some fuzzy programming models. It provides a wider decision space than if it is not used. In some cases, utilizing the min-function in a model within the General Algebraic Modeling System (GAMS) software may not lead to an optimal solution, since this function is not differentiable and the CONOPT solver cannot always find a solution to this type of model. In this paper, the importance of using the min-function in some fuzzy programming models is presented. In addition, the smooth approximation for the min-function can be utilized when the GAMS/CONOPT solver fails to reach the optimal solution of the model. A numerical example that illustrates the correctness of the proposed approach is presented.
Keywords: Fuzzy programming, Min-function, GAMS software, CONOPT solver, Smooth approximation
Cite this paper: Maged George Iskander , On Using the Min-Function in Fuzzy Programming within the GAMS Software, American Journal of Computational and Applied Mathematics , Vol. 7 No. 5, 2017, pp. 138-141. doi: 10.5923/j.ajcam.20170705.03.
Article Outline
1. Introduction
- The main philosophies of decision making in fuzzy environments were established by Bellman and Zadeh [3]. These philosophies have been used as the building blocks of fuzzy linear programming [11]. Zimmermann [10] was the first to propose fuzzy programming for solving single- and multi-objective linear programming problems. Recently, fuzzy programming has been applied to different areas of decision making. For instance, selecting projects using fuzzy linear programming [6], selecting the optimal multi-period portfolio under a fuzzy environment [9] and applying a multi-choice fuzzy linear programming problem to a garment manufacturing company [1]. In addition, using water and land resources for irrigation under uncertainty has been optimized by a multi-objective fuzzy programming method [7].In many fuzzy programming models, the decision maker seeks to optimize the membership functions, as was done by Chen and Tsai [4] and Aköz and Petrovic [2] in fuzzy goal programming. In most of these cases, the membership functions take the form of a piecewise function.The main objective of this paper is to show the importance of using the min-function in modeling some fuzzy programming problems. Moreover, since the min-function is not differentiable, its smooth approximation is utilized within the GAMS/CONOPT software.Let the linear fuzzy constraints be presented as
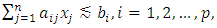 | (1) |
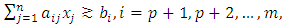 | (2) |
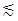 and
and 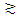 mean approximately less than or equal to and approximately greater than or equal to, respectively, xj, j = 1, 2,..., n, are non-negative decision variables, aij is the coefficient of the jth decision variable in the ith fuzzy constraint, while bi represents the right-hand side of the ith fuzzy constraint. The ith membership function for fuzzy constraints (1) and (2) is presented by (3) and (4), respectively, as follows [4]:
mean approximately less than or equal to and approximately greater than or equal to, respectively, xj, j = 1, 2,..., n, are non-negative decision variables, aij is the coefficient of the jth decision variable in the ith fuzzy constraint, while bi represents the right-hand side of the ith fuzzy constraint. The ith membership function for fuzzy constraints (1) and (2) is presented by (3) and (4), respectively, as follows [4]: 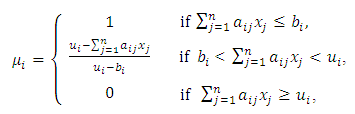 | (3) |
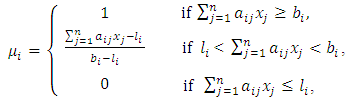 | (4) |
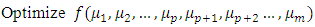 | (5) |
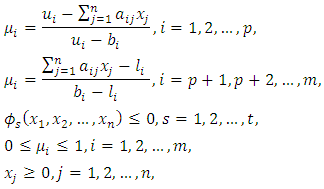 | (6) |
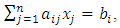 i.e., in the form of equality instead of inequality. On the other hand, the membership functions may be modeled as follows:Objective function (5), subject to:
i.e., in the form of equality instead of inequality. On the other hand, the membership functions may be modeled as follows:Objective function (5), subject to: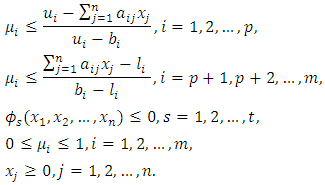 | (7) |
2. The Min-Function and Its Smooth Approximation
- In this section, the drawbacks of the above formulations are overcome by utilizing the min-function. Thus, the membership functions (3) and (4) are formulated in model (8) as follows:Objective function (5), subject to:
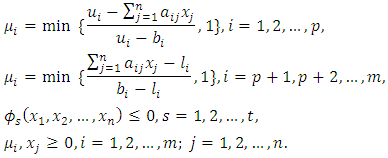 | (8) |
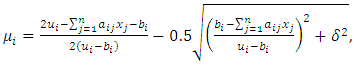 | (9) |
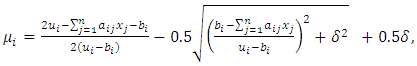 | (10) |
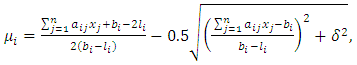 | (11) |
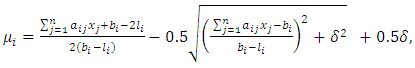 | (12) |
3. Illustrative Example
- The approach discussed above is going to be clarified by a numerical example in three different cases. Hence, consider the following three fuzzy constraints:
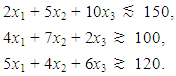 Let u1 = 170, l2 = 90, and l3 = 100. Thus, the membership functions of the three fuzzy constraints are as follows:
Let u1 = 170, l2 = 90, and l3 = 100. Thus, the membership functions of the three fuzzy constraints are as follows: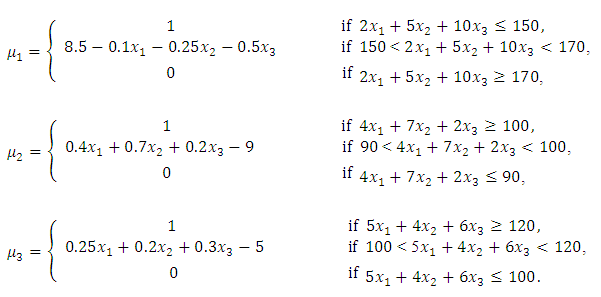 In the three cases, the objective function is to maximize μ1 + μ2 + μ3 (simple additive objective function). Also, the three fuzzy constraints are common in the three cases. One crisp constraint is considered and it is going to be changed from one case to another. The CONOPT solver embedded in GAMS win32 23.8.2 software is used in this example.The first case: Let the crisp constraint be 3x1 + 2x2 + 3x3
In the three cases, the objective function is to maximize μ1 + μ2 + μ3 (simple additive objective function). Also, the three fuzzy constraints are common in the three cases. One crisp constraint is considered and it is going to be changed from one case to another. The CONOPT solver embedded in GAMS win32 23.8.2 software is used in this example.The first case: Let the crisp constraint be 3x1 + 2x2 + 3x3 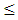 57, then the solution of model (6) is x1 = 2.937, x2 = 9.905, x3 = 9.46, μ1 = 1, μ2 = 1, and μ3 = 0.553, while the solution of model (8) is x1 = 0, x2 = 28.5, x3 = 0, μ1 = 1, μ2 = 1, and μ3 = 0.7. Even though an optimal solution exists for the two models, the solution of model (8) is better than that of model (6) since the value of the objective function in model (8) is 2.7, while in model (6) it is 2.553.The second case: Let the crisp constraint be 3x1 + 4x2 + 3x3
57, then the solution of model (6) is x1 = 2.937, x2 = 9.905, x3 = 9.46, μ1 = 1, μ2 = 1, and μ3 = 0.553, while the solution of model (8) is x1 = 0, x2 = 28.5, x3 = 0, μ1 = 1, μ2 = 1, and μ3 = 0.7. Even though an optimal solution exists for the two models, the solution of model (8) is better than that of model (6) since the value of the objective function in model (8) is 2.7, while in model (6) it is 2.553.The second case: Let the crisp constraint be 3x1 + 4x2 + 3x3 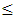 67, then the solution of model (6) is infeasible, while the solution of model (8) is x1 = 16.5, x2 = 4.375, x3 = 0, μ1 = 1, μ2 = 0.662, and μ3 = 0.The third case: Let the crisp constraint be 3x1 + 2x2 + x3
67, then the solution of model (6) is infeasible, while the solution of model (8) is x1 = 16.5, x2 = 4.375, x3 = 0, μ1 = 1, μ2 = 0.662, and μ3 = 0.The third case: Let the crisp constraint be 3x1 + 2x2 + x3 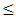 35, then the solution of model (6) is x1 = 1.316, x2 = 10.877, x3 = 9.298, μ1 = 1, μ2 = 1, and μ3 = 0.294, while for model (8) the optimal solution cannot be found due to the non-differentiability of the min-functions. Hence, the smooth approximations (9) and (11) are utilized, with δ = 0.0001, in this model. It is found that the solution is the same as the solution of model (6).It is obvious that, according to the structure of the example, model (7) gives the optimal solution. Therefore, it is used as a yardstick for the optimal solution in each case. Accordingly, in the first and the second cases, the solution of model (7) is the same as the solution of model (8), while in the third case, it is the same as the solution of model (8) when the smooth approximation is used.
35, then the solution of model (6) is x1 = 1.316, x2 = 10.877, x3 = 9.298, μ1 = 1, μ2 = 1, and μ3 = 0.294, while for model (8) the optimal solution cannot be found due to the non-differentiability of the min-functions. Hence, the smooth approximations (9) and (11) are utilized, with δ = 0.0001, in this model. It is found that the solution is the same as the solution of model (6).It is obvious that, according to the structure of the example, model (7) gives the optimal solution. Therefore, it is used as a yardstick for the optimal solution in each case. Accordingly, in the first and the second cases, the solution of model (7) is the same as the solution of model (8), while in the third case, it is the same as the solution of model (8) when the smooth approximation is used.4. Conclusions
- This paper presents an approach for modeling the membership functions in fuzzy programming when the fuzzy constraints are linear. By utilizing the min-function, the actual form of the piecewise membership functions can be effectively presented and considered within different mathematical forms and structures of fuzzy programming models. On the other side, the GAMS/CONOPT software is counted as one of the most efficient solvers. Hence, when the optimal solution of some models cannot be found due to using the min-function, an effective smooth approximation is beneficial to represent the membership functions. Eventually, the fuzzy model takes the form of a nonlinear programming model. The given numerical example illustrates the importance of the proposed methodology.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML