Md. Jahangir Hossain1, Md. Shah Alam2, Md. Babul Hossain2
1Department of Basic Science, World University of Bangladesh, Dhaka, Bangladesh
2Department of Mathematics, Mawlana Bhashani Science and Technology University, Tangail, Bangladesh
Correspondence to: Md. Babul Hossain, Department of Mathematics, Mawlana Bhashani Science and Technology University, Tangail, Bangladesh.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we mainly present fourth order Runge-Kutta (RK4) and Butcher’s fifth order Runge-Kutta (RK5) Methods for solving second order initial value problems (IVP) for ordinary differential equations (ODE). These two proposed methods are quite proficient and practically well suited for solving engineering problems based on such problems. To obtain the accuracy of the numerical solutions for this study, we have compared the approximate solutions with the exact solutions and originate a good agreement.Numerical and graphical comparisons between fourth order Runge-Kutta method and Butcher’s fifth order Runge-Kutta method have been presented. In order to, achieve more accuracy in the solution; the step size needs to be very small. Moreover, the error terms have been analyzed of these two proposed methods for different step sizesto scrutinize supremacy. A numerical example is given to exhibit the reliability and efficiency of these two methods.
Keywords:
Differential Equation, Initial Value Problem, Error analysis, Butcher’s Method, Runge-Kutta Method
Cite this paper: Md. Jahangir Hossain, Md. Shah Alam, Md. Babul Hossain, A Study on Numerical Solutions of Second Order Initial Value Problems (IVP) for Ordinary Differential Equations with Fourth Order and Butcher’s Fifth Order Runge-Kutta Methods, American Journal of Computational and Applied Mathematics , Vol. 7 No. 5, 2017, pp. 129-137. doi: 10.5923/j.ajcam.20170705.02.
1. Introduction
Most of the problems in science, mathematical physics and engineering are formulated by differential equations. The solution of differential equations is a significant part to develop the various modeling in science and engineering. There are many analytical methods for finding the solution of ordinary differential equations. But a few numbers of differential equations have analytic solutions where a large numbers of differential equations have no analytic solutions. In this case we use the numerical methods to get the approximate solution of a differential equation under the prescribed initial condition or conditions. Numerical methods are widely used for solving differential equations where it is difficult to obtain the exact solutions. There are many types of numerical methods for solving initial value problems for ordinary differential equations such as Eulers method, Runge-Kutta fourth order method (RK4). Runge-Kutta method is the powerful numerical technique to solve the initial value problems (IVP). This method widely used one since it gives reliable starting values and is particularly suitable when the computation of higher derivatives is complicated. Also this method gives more accuracy of the numerical results and used in most computer programs for a differential equation. Many authors try to spread these methods to get more accurate solution of Initial Value Problems (IVP). In [1] the author presented fifth order improved Runge-Kutta method for solving ordinary differential equation, in [2] the author presented on fifth order Runge-Kutta methods, also in [3] the author presented a comparative study on numerical solutions of Initial Value Problems (IVP) for ordinary differential equations (ODE) with Euler and Runge-Kutta methods. Also in [4-15] presented various numerical methods for finding approximations of Initial Value Problems (IVP) in ordinary differential equations (ODE). In this paper, we converted the coefficients of Butcher’s RK5 table to the general fifth order Runge-Kutta method. Also we use fourth order Runge-Kutta (RK4) and fifth order Runge-Kutta (RK5) methods for solving second order initial value problems in ordinary differential equations. Approximate solutions are compared to the exact solutions by calculate the error terms.
2. Numerical Methods
In this section we will represent two methods Runge-Kutta fourth order (RK4) and Butcher’s fifth order Runge-Kutta (RK5) methods for solving initial value problem (IVP) for ordinary differential equations (ODEs). These methods are distinguished by their order in the sense that agrees with Taylor’s series solution up to terms of 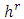 where
where 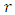 is the order of the method.Next we will apply these two methods for solving second order initial value problem.
is the order of the method.Next we will apply these two methods for solving second order initial value problem.
2.1. Runge-Kutta Fourth Order Method
We consider the following initial value problem: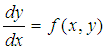 | (1) |
with initial condition 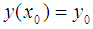 | (2) |
Now the method is based on computing 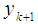 as follows:
as follows: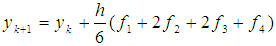 | (3) |
where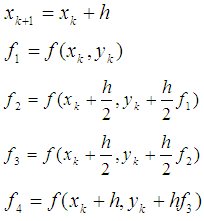 For
For 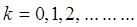
2.2. Fourth Order Runge-Kutta Method for Solving Initial Value Problem (IVP) for the System of Two Differential Equation
We consider the following system of differential equations 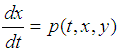 | (4) |
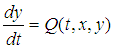 | (5) |
with the initial conditions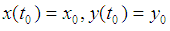 | (6) |
The fourth order RungeKutta method will become as: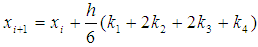 | (7) |
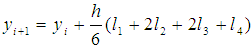 | (8) |
where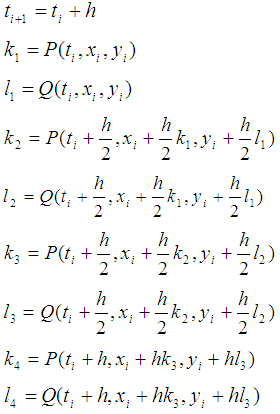
2.3. Butcher’s Fifth Order Runge-Kutta Method
We consider the following initial value problem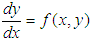 | (9) |
With initial condition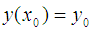 | (10) |
Now the method is based on computing 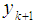 as follows
as follows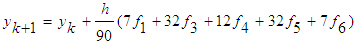 | (11) |
where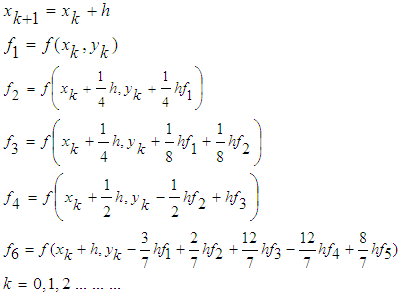
2.4. Butcher’s Fifth Order Runge-Kutta Method for Solving Initial Value Problem (IVP) for the System of Two Differential Equations
We consider the following system of differential equations: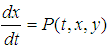 | (12) |
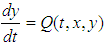 | (13) |
with the initial conditions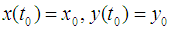 | (14) |
The Butcher’s fifth order Runge-Kutta method will become as: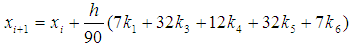 | (15) |
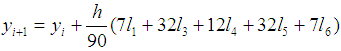 | (16) |
Where 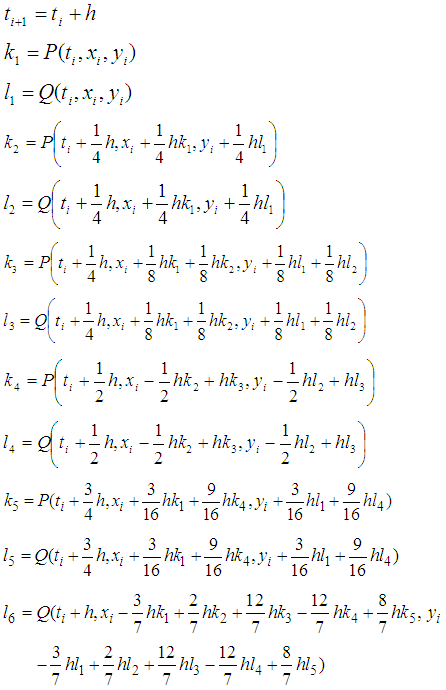 For
For 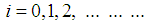
3. Error Analysis
Our main goal is to find the more accurate results in numerical solutions of ordinary differential equations. There are two types of errors occurs (Truncation errors and Round-off errors). Truncation error in numerical analysis arises when approximations are used to estimate some quantity. Rounding errors originate from the fact that computer can only represent a limited number of significant figures. Thus, such numbers cannot be represented exactly in computer memory. The discrepancy introduced by this limitation is called Round-off error. The accuracy of the solution will depend on how small we take the step size, 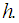 A numerical method is said to be convergent if the numerical solution approaches the exact solution as the step size
A numerical method is said to be convergent if the numerical solution approaches the exact solution as the step size 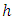 tends to zero. The convergence of initial value problem is calculated by
tends to zero. The convergence of initial value problem is calculated by 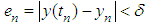 where
where 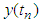 denotes the approximate solution and
denotes the approximate solution and 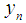 denotes the exact solution and
denotes the exact solution and 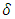 depends on the problem which varies from 10-5. The errors for these two formulas are defined by
depends on the problem which varies from 10-5. The errors for these two formulas are defined by 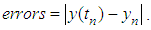
4. Illustrative Example
In this section, we illustrate a second order initial value problem as numerical example to compare between these two methods. All the computations are performed by MATLAB software. Numerical results and errors are computed and the outcomes are represented by graphically.Example:Consider the initial value problem 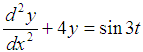 | (17) |
with the initial conditions 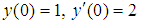 on the interval
on the interval 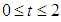 . The exact solution of this initial value problem is given by
. The exact solution of this initial value problem is given by 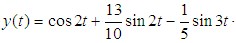 Now this second order initial value problem can be written in the form of system of first order differential equations by putting
Now this second order initial value problem can be written in the form of system of first order differential equations by putting 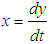 as
as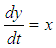 | (18) |
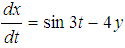 | (19) |
with the initial conditions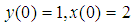 | (20) |
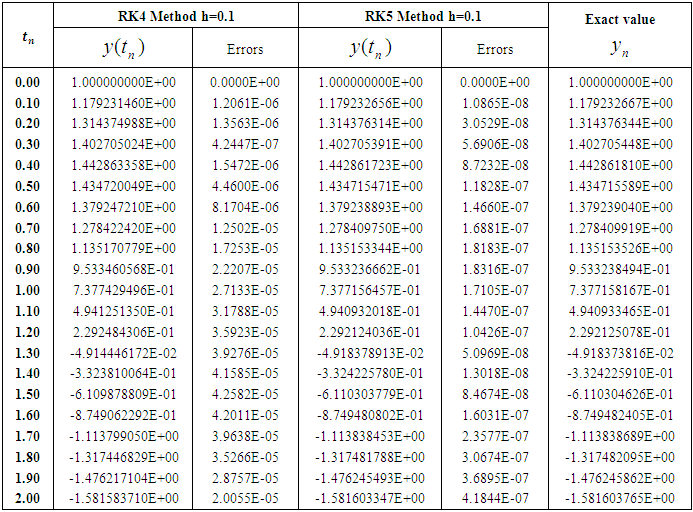
The approximate results, exact results and maximum errors for step sizes 0.1, 0.05, 0.025 and 0.0125 are shown in Tables 1-4 and the graphs of the numerical solutions are displayed in Figures 1-8.Table 1. Numerical approximations and maximum errors for step size h=0.1
 |
| |
|
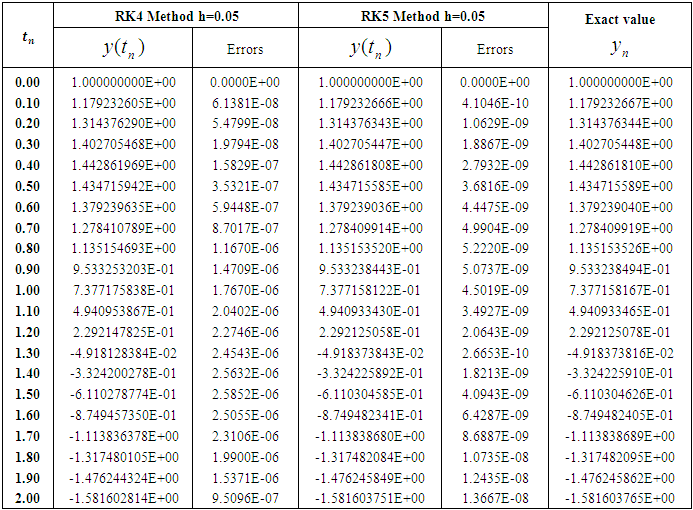
Table 2. Numerical approximations and maximum errors for step size h=0.05
 |
| |
|
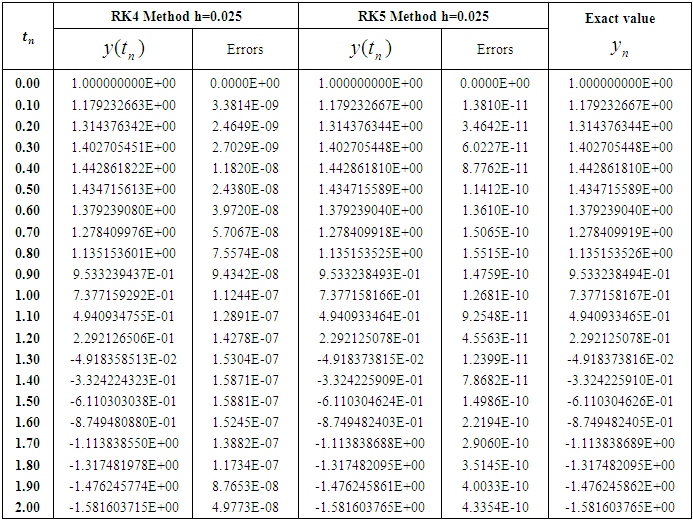
Table 3. Numerical approximations and maximum errors for step size h=0.025
 |
| |
|
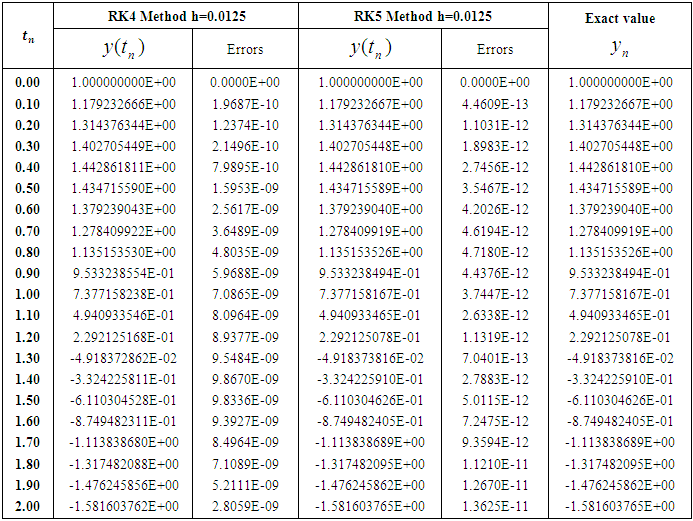
Table 4. Numerical approximations and maximum errors for step size h=0.0125
 |
| |
|
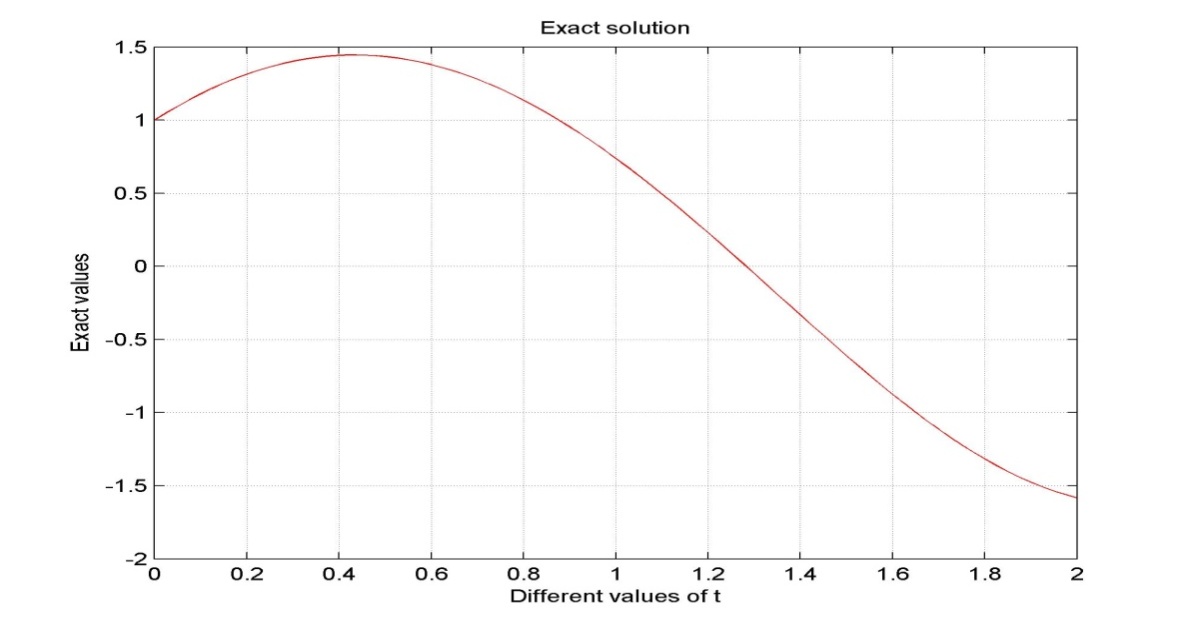 | Figure 1. Exact numerical solutions |
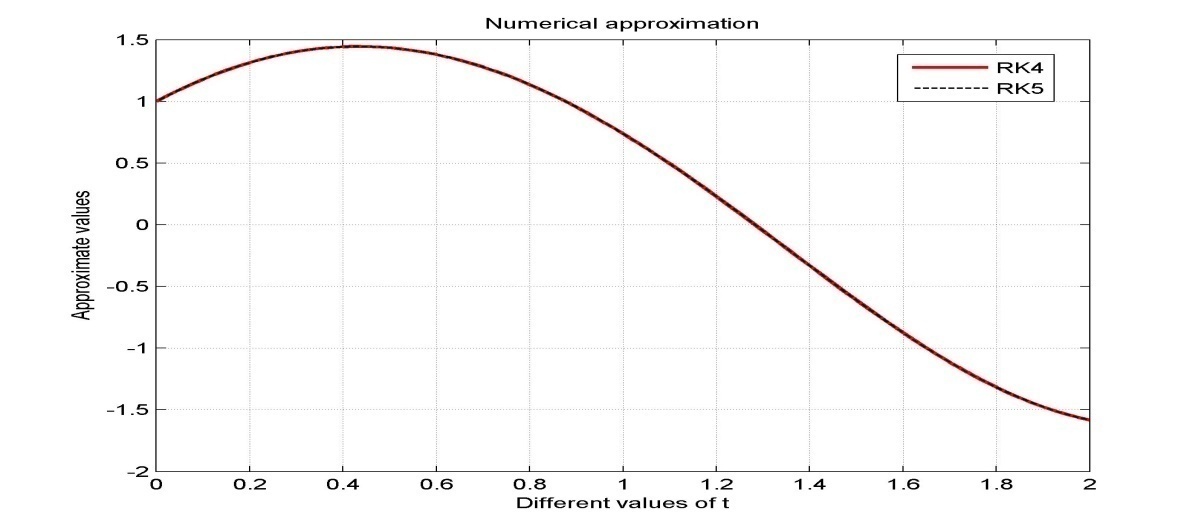 | Figure 2. Approximate numerical solutions |
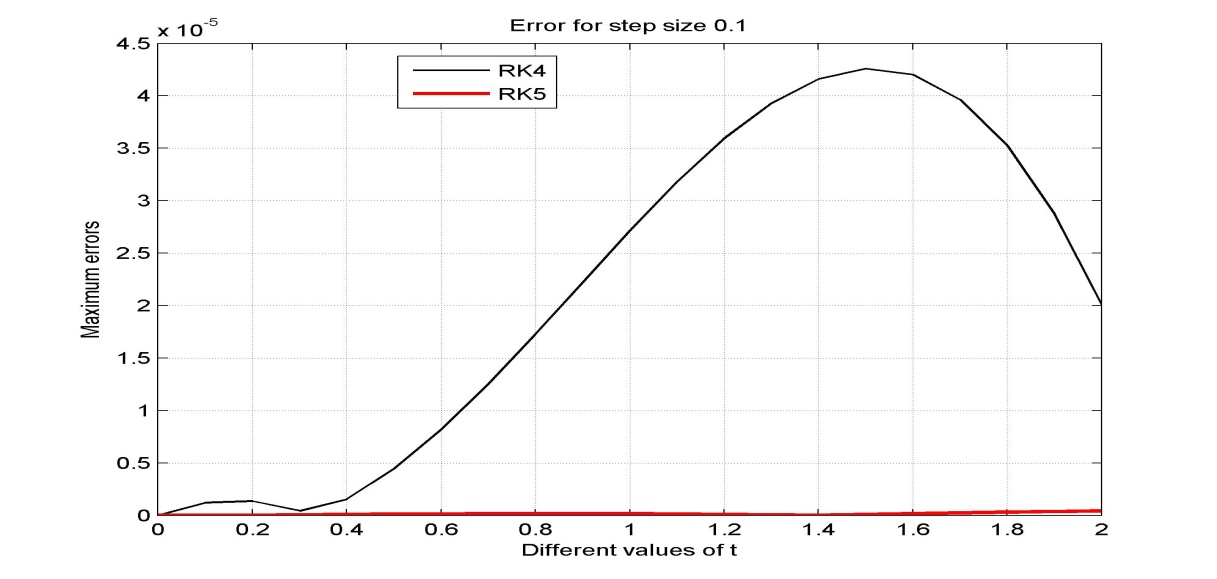 | Figure 3. Error for step size h=0.1 |
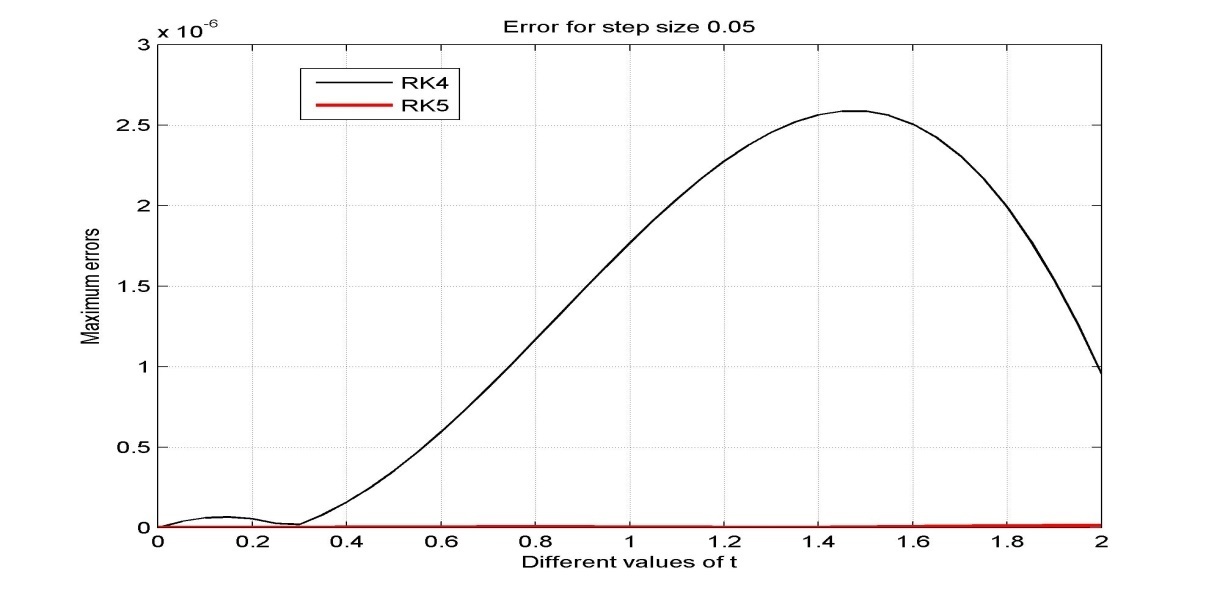 | Figure 4. Error for step size h=0.05 |
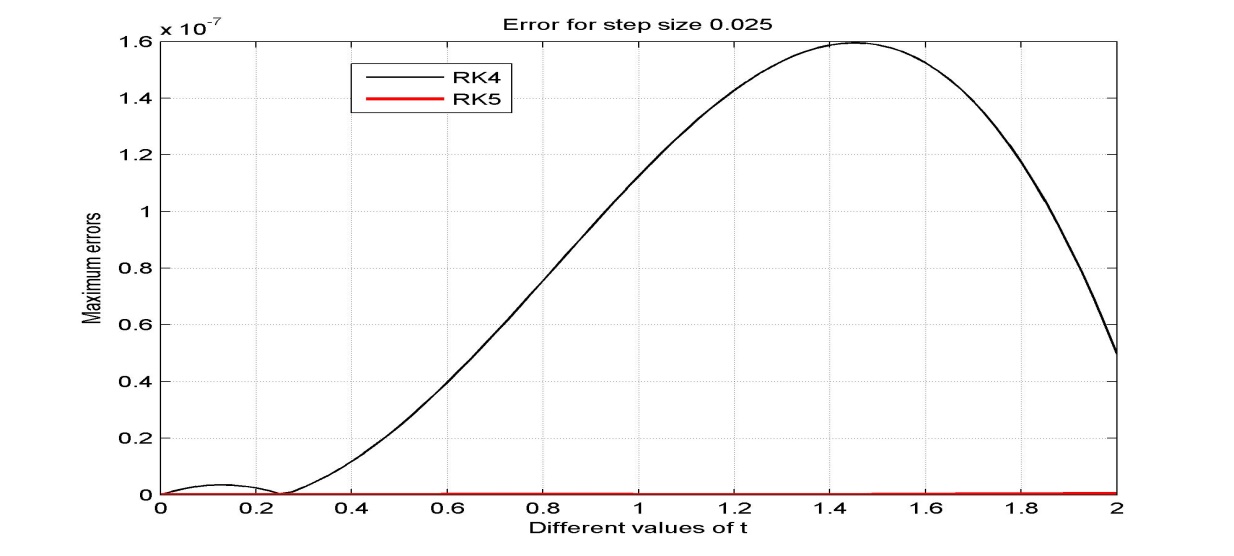 | Figure 5. Error for step size h=0.025 |
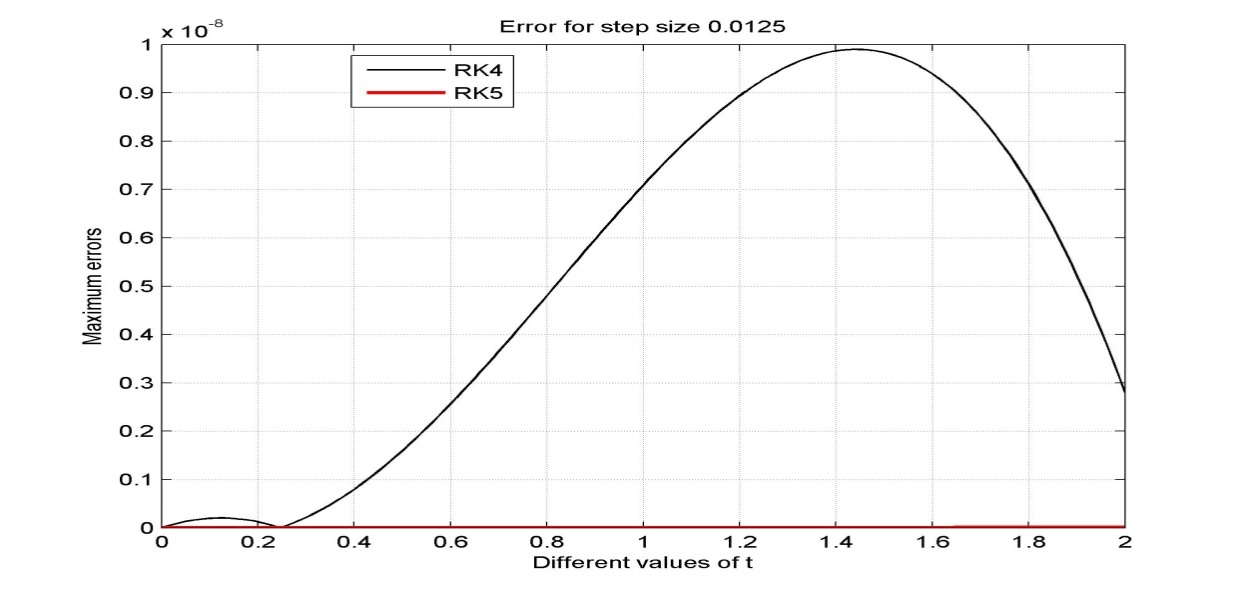 | Figure 6. Error for step size h=0.0125 |
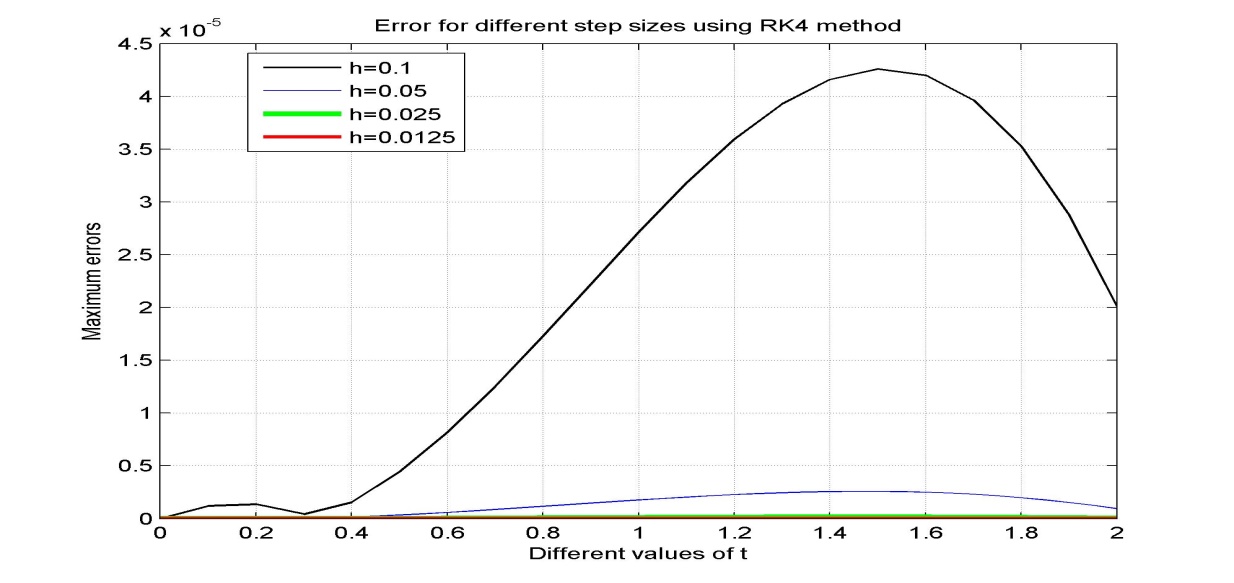 | Figure 7. Error for different step sizes using RK4 method |
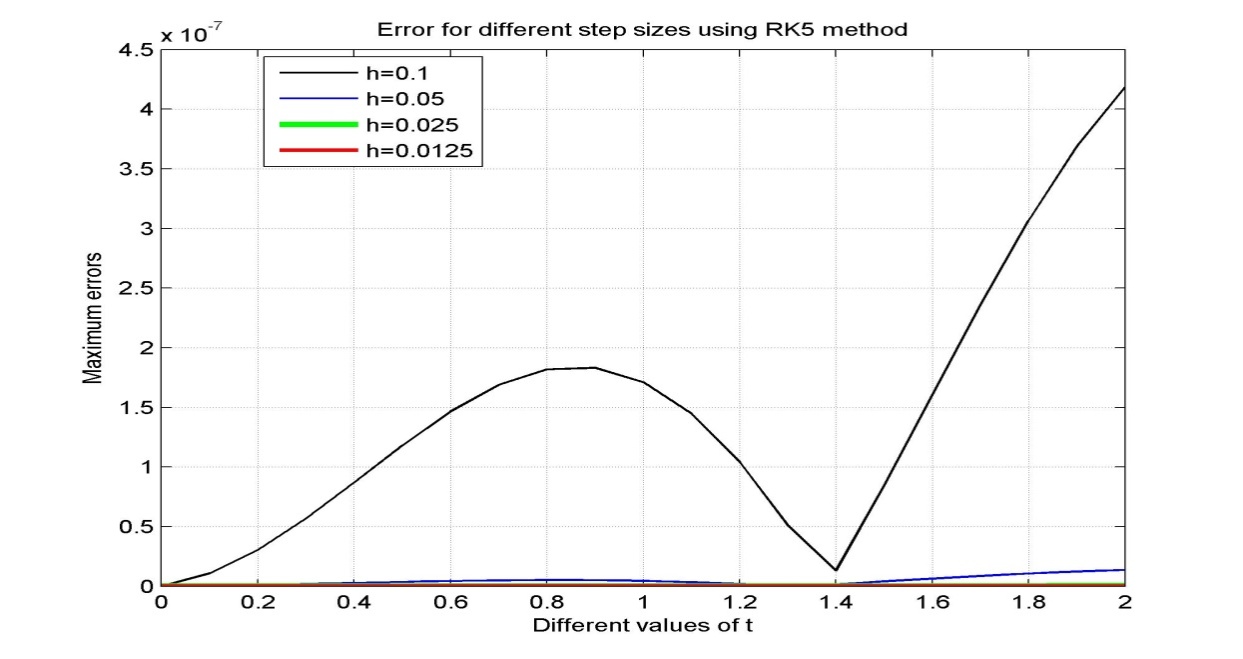 | Figure 8. Error for different step sizes using RK5 method |
5. Discussion
The acquired results are displayed in Tables (1-4) and graphically presented in Figures (1-8). The approximate solutions and errors are calculated with the step sizes 0.1, 0.05, 0.025 and 0.0125 by using MATLAB. The approximate solutions are compared to the exact solutions. The Runge-Kutta fifth order (RK5) approximations for same step size converge to exact solution. It is also mention that the small step size provides the better approximation. We observe that from Tables (1-4) Runge-Kutta fifth order (RK5) method gives more accurate results and better than Runge-Kutta fourth order (RK4) method. Also from figures 7 and 8 we conclude that if the step size tends to zero then the errors also tends to zero.
6. Conclusions
In this paper, fourth order Runge-Kutta method and Butcher’s fifth order Runge-Kutta method are applied to solve second order initial value problems (IVP) of ordinary differential equation (ODE). To find more accurate results we need to reduce the step size for both methods. From the resulting tables and figures we analyzed that both methods converge to the exact solutions for very small values of the step size, h. From the figure 2 we also observe that both methods give almost same results but from Figures 3-6 it is clear that RK5 method gives more accurate results than RK4 method. Also we state that the Butcher’s fifth order Runge-Kutta method is more appropriate and proficient for finding the numerical solutions of initial value problems (IVP) than fourth order Runge-Kutta method. Hence from this study we conclude that to find more accurate result higher order numerical method is appropriate than lower order methods.
References
| [1] | Rabiei, F., & Ismail, F. (2012). Fifth-order Improved Runge-Kutta method for solving ordinary differential equation. Australian Journal of Basic and Applied Sciences, 6(3), 97-105. |
| [2] | Butcher, J. C. (1995). On fifth order Runge-Kutta methods. BIT Numerical Mathematics, 35(2), 202-209. |
| [3] | Islam, M. A. (2015). A Comparative Study on Numerical Solutions of Initial Value Problems (IVP) for Ordinary Differential Equations (ODE) with Euler and RungeKutta Methods. American Journal of Computational Mathematics, 5(03), 393. |
| [4] | Butcher, J. C. (1964). On Runge-Kutta processes of high order. Journal of the Australian Mathematical Society, 4(02), 179-194. |
| [5] | Islam, M. A. (2015). Accuracy Analysis of Numerical solutions of Initial Value Problems (IVP) for Ordinary Differential Equations (ODE). IOSR Journal of Mathematics, 11, 18-23. |
| [6] | Butcher, J. C. (1996). A history of Runge-Kutta methods. Applied numerical mathematics, 20(3), 247-260. |
| [7] | Goeken, D., & Johnson, O. (2000). Runge–Kutta with higher order derivative approximations. Applied numerical mathematics, 34(2-3), 207-218. |
| [8] | Lambert, J. D. (1973). Computational methods in ordinary differential equations. Wiley, New York. |
| [9] | Mathews, J.H. (2005). Numerical Methods for Mathematics, Science and Engineering. Prentice-Hall, India. |
| [10] | Hall, G. and Watt, J.M. (1976). Modern Numerical Methods for Ordinary Differential Equations. Oxford University Press, Oxford. |
| [11] | Burden, R.L. and Faires, J.D. (2002). Numerical Analysis. Bangalore, India. |
| [12] | Gerald, C.F. and Wheatley, P.O. (2002). Applied Numerical Analysis. Pearson Education, India. |
| [13] | Hossain, Md.S., Bhattacharjee, P.K. and Hossain, Md.E. (2013). Numerical Analysis. Titas Publications, Dhaka. |
| [14] | Sastry, S.S. (2000). Introductory Methods of Numerical Analysis. Prentice-Hall, India. |
| [15] | Balagurusamy, E. (2006). Numerical Methods. Tata McGraw-Hill, New Delhi. |



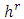 where
where 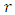 is the order of the method.Next we will apply these two methods for solving second order initial value problem.
is the order of the method.Next we will apply these two methods for solving second order initial value problem. 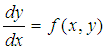
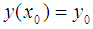
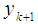 as follows:
as follows: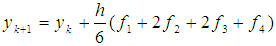
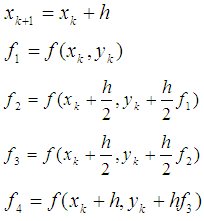 For
For 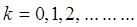
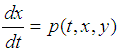
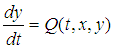
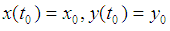
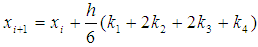
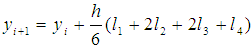
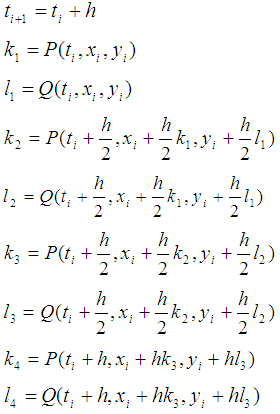
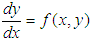
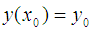
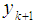 as follows
as follows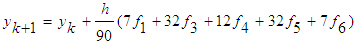
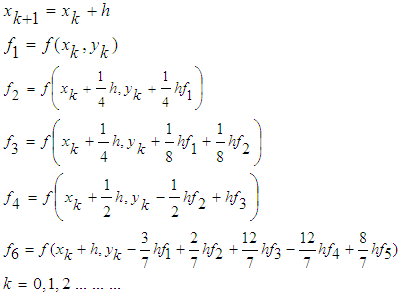
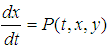
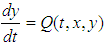
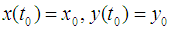
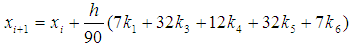
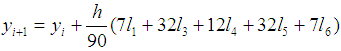
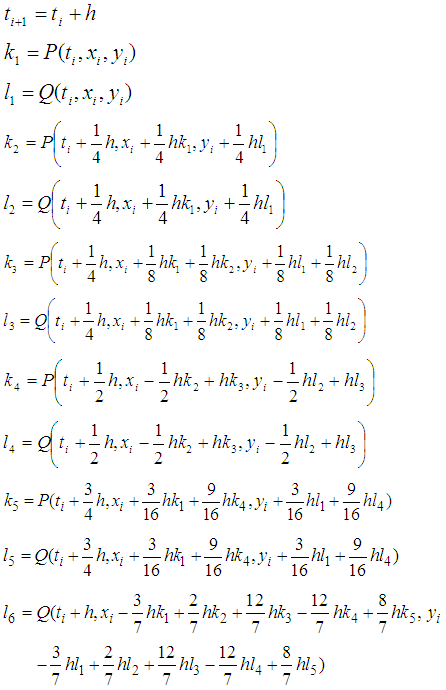 For
For 
 A numerical method is said to be convergent if the numerical solution approaches the exact solution as the step size
A numerical method is said to be convergent if the numerical solution approaches the exact solution as the step size 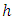 tends to zero. The convergence of initial value problem is calculated by
tends to zero. The convergence of initial value problem is calculated by 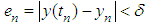 where
where 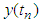 denotes the approximate solution and
denotes the approximate solution and 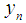 denotes the exact solution and
denotes the exact solution and 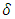 depends on the problem which varies from 10-5. The errors for these two formulas are defined by
depends on the problem which varies from 10-5. The errors for these two formulas are defined by 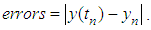
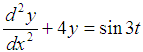
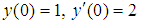 on the interval
on the interval 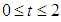 . The exact solution of this initial value problem is given by
. The exact solution of this initial value problem is given by 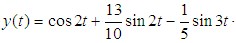 Now this second order initial value problem can be written in the form of system of first order differential equations by putting
Now this second order initial value problem can be written in the form of system of first order differential equations by putting 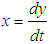 as
as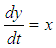
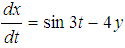
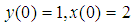








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


