Iwundu M. P.
Department of Mathematics and Statistics, University of Port Harcourt, Nigeria
Correspondence to: Iwundu M. P., Department of Mathematics and Statistics, University of Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The bahaviours of the first compound of the hat matrix and the determinant-based loss criterion are examined for effects of a missing observation in three configurations of six-factor central composite design, varying in factorial portion. The hat matrix varies between one design configuration and another but remains unchanged within same design configuration with different defining relations. The diagonal entries of each corresponding hat matrix associated with a factorial point, an axial point and a center point respectively correspond to the losses computed using the determinant-based criterion. Loss due to missing center point in the three categories of design is very minimal when compared with loss due to either missing factorial point or missing axial point. The configuration with one-quarter fractional factorial portion attracts significantly higher losses to a missing observation of either factorial, axial or center portion when compared with either the configuration with one-half fractional factorial portion or the configuration with complete factorial portion. This is possibly because the configuration with one-quarter fractional factorial portion is near saturated. Variances associated with parameter estimates are minimum for the design category with complete factorial portion and maximum for the design category with one-quarter fractional factorial portion. Interestingly, the design category that minimizes the variances also minimizes the losses.
Keywords:
Missing observations, Compound of hat matrix, Fractional replicates, Loss criterion, Central composite design
Cite this paper: Iwundu M. P., On the Compounds of Hat Matrix for Six-Factor Central Composite Design with Fractional Replicates of the Factorial Portion, American Journal of Computational and Applied Mathematics , Vol. 7 No. 4, 2017, pp. 95-114. doi: 10.5923/j.ajcam.20170704.02.
1. Introduction
The concept of hat matrix plays a major role in modeling and is commonly encountered in regression and analysis of variance problems. Hoaglin and Welsch [11] linked its origin to John Tukey who is said to have introduced the matrix in the 1960s. Historically, the name takes its bearing from the fact that for a linear model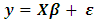 | (1) |
the least squares estimate of β is 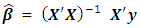 Thus the fitted or estimated value is
Thus the fitted or estimated value is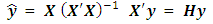 | (2) |
where 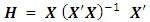 is called the hat matrix and puts the “hat” on the vector of fitted or estimated value. Of course, as a projection matrix, the hat matrix projects y into
is called the hat matrix and puts the “hat” on the vector of fitted or estimated value. Of course, as a projection matrix, the hat matrix projects y into 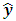 in the model space. In a simpler language, the hat matrix converts values from the observed variable into estimates. In equation (1), y denotes the vector of observations, X denotes the model matrix, β denotes the vector of unknown parameters which are estimated on the basis of N uncorrelated observations and ε denotes the random error component assumed normally and independently distributed with zero mean and constant variance. One major role of the hat matrix in modeling problems is in identifying observations that have greater impacts on the estimation of model parameters and fitted values. Identifying and dealing with such observations help improve statistical inferences. The mention of hat matrix automatically directs one’s mind to leverage which according to Myung and Kahng [12] is one of the basic components of influence in linear regression models. Each diagonal element
in the model space. In a simpler language, the hat matrix converts values from the observed variable into estimates. In equation (1), y denotes the vector of observations, X denotes the model matrix, β denotes the vector of unknown parameters which are estimated on the basis of N uncorrelated observations and ε denotes the random error component assumed normally and independently distributed with zero mean and constant variance. One major role of the hat matrix in modeling problems is in identifying observations that have greater impacts on the estimation of model parameters and fitted values. Identifying and dealing with such observations help improve statistical inferences. The mention of hat matrix automatically directs one’s mind to leverage which according to Myung and Kahng [12] is one of the basic components of influence in linear regression models. Each diagonal element 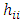 of the hat matrix is called leverage and measures the extent to which the fitted regression model
of the hat matrix is called leverage and measures the extent to which the fitted regression model 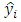 is attracted by the given observation or data point
is attracted by the given observation or data point 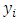 . In essence, the
. In essence, the 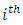 leverage
leverage 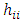 quantifies the influence that the observation
quantifies the influence that the observation 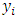 has on its predicted value
has on its predicted value 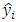 . The diagonal elements of the hat matrix are such that
. The diagonal elements of the hat matrix are such that 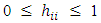 and
and 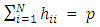 ; where N is the number of data points and p is the number of model parameters, including the intercept. Aside investigating whether one or more observations excessively influence the estimated values, the hat matrix may also be used to quantify the effect of removing one or more observations from a design. Thus, the hat matrix (through its compounds) is useful in understanding effect of alterations to a complete data set. By the alterations, a removed observation is seen as a missing observation. It is desirable to have the effect of missing observations as mild as possible. The term “Robust” first introduced by Box [9] is quite often encountered when studying the effects of missing observations. Akhtar [1] considered the effect of missing observations on the determinant of information matrix. Akhtar [6] considered the effect of missing observations on some configurations of five-factor central composite design and compared the variances of the parameter estimates as well as the sum of variances for each design configuration. Akram [7] assessed the effects of missing observation on the estimates of model parameters. Designs robust to missing observations have been considered by Ahmad and Gilmour [4] and Ahmad et al. [5] using minimax loss criterion. Chukwu et al. [10] considered the robustness of Split-plot central composite designs in the presence of a single missing observation. In their work, minimaxloss criterion, based on D-efficiency, and which accounts for the within-whole plot correlation among the observations, was presented for constructing split-plot response surface designs that are robust to missing a single observation of the various design points. Okon and Nsude [13] investigated alpha values for which the four-factor central composite designs are robust to a pair of missing observations under the minimaxloss criterion. Yakubu et al. [16] considered the impact of single missing observations of the various composite design points on estimation and predictive capability of central composite designs. Some economical designs have been constructed and studied for their robustness to missing data by Ahmad and Akhtar [3]. In studying robust response surface designs against missing observations, Srisuradetchai [15] considered the sensitivity of small second-order designs through the loss of D-efficiency and established the impact of missing observations on predictive variances. Smucker et al. [14] considered the robustness of classical and optimal designs to missing observations using D- and I-efficiencies. Based on recommendation of Akhtar [6] to investigate models with more than five input variables, the effect of a missing observation in six-factor central composite design is considered in this paper. Particular interest is in robustness of fractional replicates of the factorial portion of the six-factor central composite design. Comparison of the effect of a missing observation shall be made using the first compound of the hat matrix.
; where N is the number of data points and p is the number of model parameters, including the intercept. Aside investigating whether one or more observations excessively influence the estimated values, the hat matrix may also be used to quantify the effect of removing one or more observations from a design. Thus, the hat matrix (through its compounds) is useful in understanding effect of alterations to a complete data set. By the alterations, a removed observation is seen as a missing observation. It is desirable to have the effect of missing observations as mild as possible. The term “Robust” first introduced by Box [9] is quite often encountered when studying the effects of missing observations. Akhtar [1] considered the effect of missing observations on the determinant of information matrix. Akhtar [6] considered the effect of missing observations on some configurations of five-factor central composite design and compared the variances of the parameter estimates as well as the sum of variances for each design configuration. Akram [7] assessed the effects of missing observation on the estimates of model parameters. Designs robust to missing observations have been considered by Ahmad and Gilmour [4] and Ahmad et al. [5] using minimax loss criterion. Chukwu et al. [10] considered the robustness of Split-plot central composite designs in the presence of a single missing observation. In their work, minimaxloss criterion, based on D-efficiency, and which accounts for the within-whole plot correlation among the observations, was presented for constructing split-plot response surface designs that are robust to missing a single observation of the various design points. Okon and Nsude [13] investigated alpha values for which the four-factor central composite designs are robust to a pair of missing observations under the minimaxloss criterion. Yakubu et al. [16] considered the impact of single missing observations of the various composite design points on estimation and predictive capability of central composite designs. Some economical designs have been constructed and studied for their robustness to missing data by Ahmad and Akhtar [3]. In studying robust response surface designs against missing observations, Srisuradetchai [15] considered the sensitivity of small second-order designs through the loss of D-efficiency and established the impact of missing observations on predictive variances. Smucker et al. [14] considered the robustness of classical and optimal designs to missing observations using D- and I-efficiencies. Based on recommendation of Akhtar [6] to investigate models with more than five input variables, the effect of a missing observation in six-factor central composite design is considered in this paper. Particular interest is in robustness of fractional replicates of the factorial portion of the six-factor central composite design. Comparison of the effect of a missing observation shall be made using the first compound of the hat matrix.
2. Theoretical Background
For a symmetric matrix 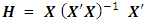 of order N, the mth compound of H is a matrix of order
of order N, the mth compound of H is a matrix of order 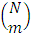 , where N is the number of data points in the complete design and m is the number of missing observations. The mth compound of H is formed by the elements of which are minors of
, where N is the number of data points in the complete design and m is the number of missing observations. The mth compound of H is formed by the elements of which are minors of 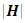 of order m. All possible minors that are
of order m. All possible minors that are 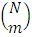 from the same combination of rows (or columns) of H are placed in the same rows (or columns) of the mth compound of H say
from the same combination of rows (or columns) of H are placed in the same rows (or columns) of the mth compound of H say 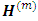 . The elements of
. The elements of 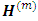 are arranged in lexicographic (or lexical) order. The first compound of the hat matrix is the hat matrix itself. For more on compounds of the hat matrix, see Akram [7] and Atken and Rutherford [8]. In studying the effect of missing observations, Akhar and Prescot [2] defined loss as the relative reduction in the determinant of information matrix associated with the complete design. In this context, a complete design
are arranged in lexicographic (or lexical) order. The first compound of the hat matrix is the hat matrix itself. For more on compounds of the hat matrix, see Akram [7] and Atken and Rutherford [8]. In studying the effect of missing observations, Akhar and Prescot [2] defined loss as the relative reduction in the determinant of information matrix associated with the complete design. In this context, a complete design 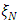 is an N-point design constructed according to response surface model and having no missing data point. A six-factor central composite complete design with full replicate of factorial portion, full replicate of axial portion and four replicates of center portion constructed for a second-order complete model in twenty-eight parameters has eighty data points. The associated design matrix is a matrix of order (80x6). The associated model matrix X is a matrix of order (80x28). The information matrix associated with the complete design is the matrix which is of order (28x28). Generally, an information matrix,
is an N-point design constructed according to response surface model and having no missing data point. A six-factor central composite complete design with full replicate of factorial portion, full replicate of axial portion and four replicates of center portion constructed for a second-order complete model in twenty-eight parameters has eighty data points. The associated design matrix is a matrix of order (80x6). The associated model matrix X is a matrix of order (80x28). The information matrix associated with the complete design is the matrix which is of order (28x28). Generally, an information matrix, 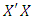 , of a design is a
, of a design is a 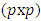 matrix, where p represents the number of model parameters. When an observation or data point in the design is lost or missing, the matrix X reduces by one row. Similarly, when m observations or data points in the design are lost or missing, the matrix X reduces by m rows. As expected, the information matrix, say
matrix, where p represents the number of model parameters. When an observation or data point in the design is lost or missing, the matrix X reduces by one row. Similarly, when m observations or data points in the design are lost or missing, the matrix X reduces by m rows. As expected, the information matrix, say 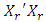 , for the reduced design will be diffierent from the information matrix,
, for the reduced design will be diffierent from the information matrix, 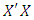 , for the complete design. For (mxp) matrix of m missing rows,
, for the complete design. For (mxp) matrix of m missing rows, 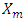 , corresponding to the m missing observations, the complete information matrix may be written as
, corresponding to the m missing observations, the complete information matrix may be written as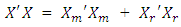 | (3) |
By post multiplication,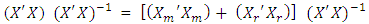 | (4) |
This implies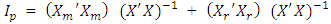 ;
; 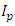 is an identity matrix of order p.By rearrangement we have
is an identity matrix of order p.By rearrangement we have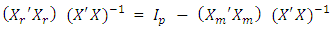 | (5) |
Post multiplying by 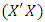 yields
yields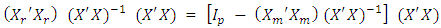 | (6) |
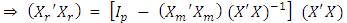 | (7) |
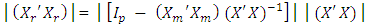 | (8) |
This implies 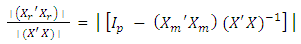 | (9) |
Akhtar [1] calls  the diagonal element of the mth compound of (I−H) where H is the hat matrix according to the m missing points and I is an identity matrix of same dimension as H. The loss due to a single missing observation is defined as
the diagonal element of the mth compound of (I−H) where H is the hat matrix according to the m missing points and I is an identity matrix of same dimension as H. The loss due to a single missing observation is defined as 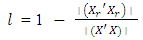 | (10) |
and relates to the corresponding diagonal element of the first compound of the hat matrix H.
3. Configurations of the Six-factor Central Composite Design
The loss due to missing observations of the six-factor central composite design shall be examined under three Configurations;Case 1: k = 6, one replicate of factorial portion, one replicate of axial portion and four replicates of center portion.Case 2: k = 6, one-half replicate of factorial portion, one replicate of axial portion and four replicates of center portion.Case 3: k = 6, one-quarter replicate of factorial portion, one replicate of axial portion and four replicates of center portion.By these three configurations, nonsingular information matrices may be obtained. Case 1 allows a complete design of size N = 80 to be examined. The factorial portion comprises of design points associated with full 26 factorial design. The axial portion comprises of the design points {(± 1,0,0,0,0,0), (0, ± 1,0,0,0,0), (0,0, ± 1,0,0,0), (0,0,0, ± 1,0,0), (0,0,0,0, ± 1,0), (0,0,0,0,0, ± 1)}. The center portion comprises of the design point (0,0,0,0,0,0) repeated four times.Case 2 allows a complete design of size N = 48 to be examined. The factorial portion comprises of design points associated with one-half fractional replicate of 26 factorial design. The factorial portion may be obtained using the defining relation I = +ABCDEF or I = −ABCDEF. The axial portion comprises of the design points {(± 1,0,0,0,0,0), (0, ± 1,0,0,0,0), (0,0, ± 1,0,0,0), (0,0,0, ± 1,0,0), (0,0,0,0, ± 1,0), (0,0,0,0,0, ± 1)}. The center portion comprises of the design point (0,0,0,0,0,0) repeated four times. Case 3 allows a complete design of size N = 32 to be examined. The factorial portion comprises of design points associated with one-quarter fractional replicate of 26 factorial design. The factorial portion may be obtained using the defining relation I = +ABC and I = +DEF or I = +ABC and I = −DEF or I = −ABC and I = −DEF or I = −ABC and I = +DEF. The axial portion comprises of the design points {(± 1,0,0,0,0,0), (0, ± 1,0,0,0,0), (0,0, ± 1,0,0,0), (0,0,0, ± 1,0,0), (0,0,0,0, ± 1,0), (0,0,0,0,0, ± 1)}. The center portion comprises of the design point (0,0,0,0,0,0) repeated four times. The use of fractional factorials greatly reduces the required experimental runs. In fact, Case 3 brings the design to near-saturated. Using the defining relations I = +ABCDEF, the alises of effects under Case 2 are as follows;
 Using the defining relations I = +ABC and I = +DEF alongside the generalized interaction I = +ABCDEF, the alises of effects under Case 3 are as follows;
Using the defining relations I = +ABC and I = +DEF alongside the generalized interaction I = +ABCDEF, the alises of effects under Case 3 are as follows;
4. Results
4.1. Six-factor Central Composite Design with One Replicate of Factorial Portion, One Replicate of Axial Portion and Four Replicates of Center Portion
The hat matrix 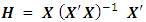 associated with complete cuboidal six-factor central composite design having one replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix
associated with complete cuboidal six-factor central composite design having one replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix 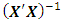 whose elements are as in the immediate.
whose elements are as in the immediate. | Tab. 4.1 |
Trace 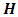 = 28.0000det
= 28.0000det 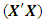 = 1.5533e+043 det
= 1.5533e+043 det 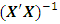 = 6.4379e-044For a missing observation, the 80-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet
= 6.4379e-044For a missing observation, the 80-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet 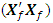 = 1.0238e+043 det
= 1.0238e+043 det 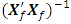 = 9.7674e-044
= 9.7674e-044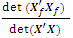 = 0.6591The loss due to missing vertex point is
= 0.6591The loss due to missing vertex point is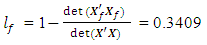 This corresponds to the first entry, 0.3409, of the hat matrix in Appendix A. Associated with a missing axial point is the determinantdet
This corresponds to the first entry, 0.3409, of the hat matrix in Appendix A. Associated with a missing axial point is the determinantdet 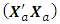 = 7.9503e+042det
= 7.9503e+042det 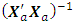 = 1.2578e-043
= 1.2578e-043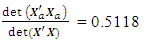 The loss due to missing axial point is
The loss due to missing axial point is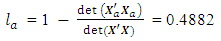 This corresponds to the 65th entry, 0.4882, of the hat matrix in Appendix A. Associated with a missing center point is the determinantdet
This corresponds to the 65th entry, 0.4882, of the hat matrix in Appendix A. Associated with a missing center point is the determinantdet 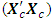 = 1.4269e+043det
= 1.4269e+043det 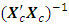 = 7.0081e-044
= 7.0081e-044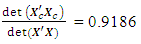 The loss due to missing center point is
The loss due to missing center point is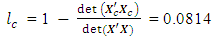 This corresponds to the 80th entry, 0.0814, of the hat matrix in Appendix A.The variances of parameter estimates for the complete and reduced designs are as in Table 1.
This corresponds to the 80th entry, 0.0814, of the hat matrix in Appendix A.The variances of parameter estimates for the complete and reduced designs are as in Table 1. 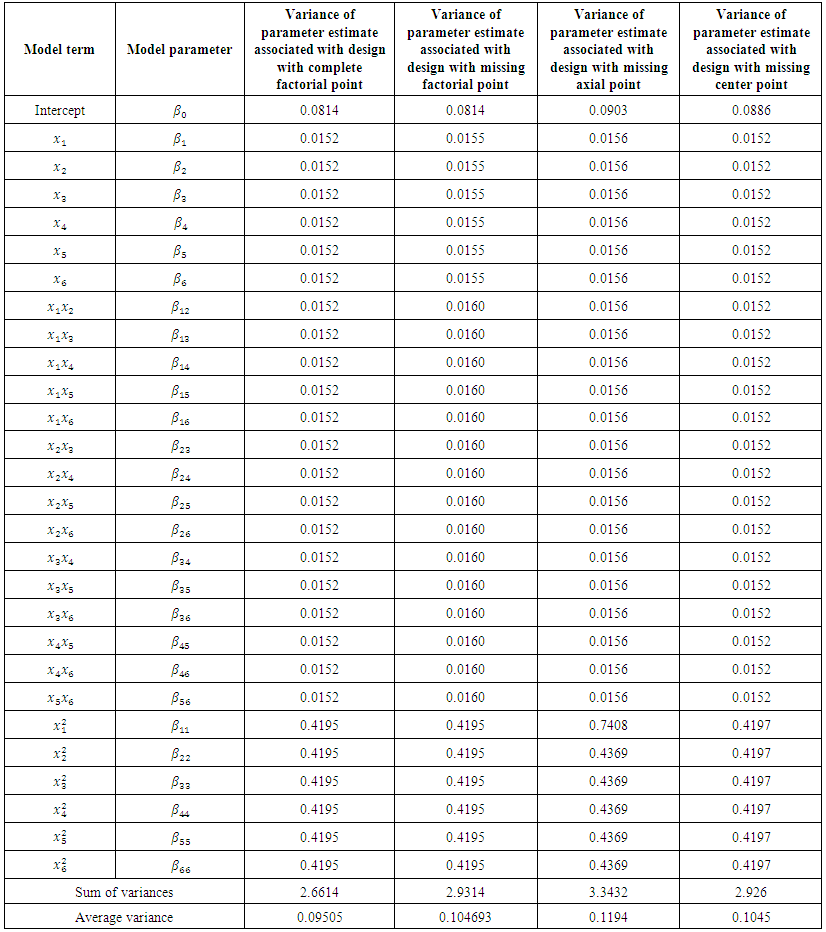 | Table 1. Variances of parameter estimates for the complete and reduced designs (one replicate of factorial portion) |
4.2. Six-factor Central Composite Design with One-Half Replicate of Factorial Portion, One Replicate of Axial Portion and four Replicates of Center Portion
The hat matrix 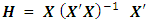 associated with complete cuboidal six-factor central composite design having one-half replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix B. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix
associated with complete cuboidal six-factor central composite design having one-half replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix B. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix 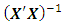 whose elements are as in the immediate.
whose elements are as in the immediate. | Tab. 4.2 |
Trace 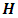 = 28.0000det
= 28.0000det 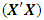 = 4.4373e+036det
= 4.4373e+036det 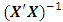 = 2.2536e-037For a missing observation, the 48-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet
= 2.2536e-037For a missing observation, the 48-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet 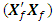 = 1.4361e+036det
= 1.4361e+036det 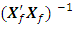 = 6.9635e-037
= 6.9635e-037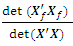 = 0.3236The loss due to missing vertex point is
= 0.3236The loss due to missing vertex point is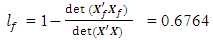 This corresponds to the first entry, 0.6764, of the hat matrix in Appendix B. Associated with a missing axial point is the determinantdet
This corresponds to the first entry, 0.6764, of the hat matrix in Appendix B. Associated with a missing axial point is the determinantdet 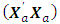 = 2.2077e+036det
= 2.2077e+036det 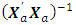 = 4.5297e-037
= 4.5297e-037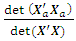 = 0.4975The loss due to missing axial point is
= 0.4975The loss due to missing axial point is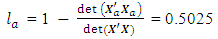 This corresponds to the 65th entry, 0.5025, of the hat matrix in Appendix B. Associated with a missing center point is the determinantdet
This corresponds to the 65th entry, 0.5025, of the hat matrix in Appendix B. Associated with a missing center point is the determinantdet 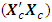 = 4.0750e+036det
= 4.0750e+036det 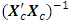 = 2.4540e-037
= 2.4540e-037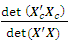 = 0.9184The loss due to missing center point is
= 0.9184The loss due to missing center point is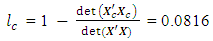 This corresponds to the 80th entry, 0.0816, of the hat matrix in Appendix B.The variances of parameter estimates for the complete and reduced designs are as in Table 2.
This corresponds to the 80th entry, 0.0816, of the hat matrix in Appendix B.The variances of parameter estimates for the complete and reduced designs are as in Table 2. 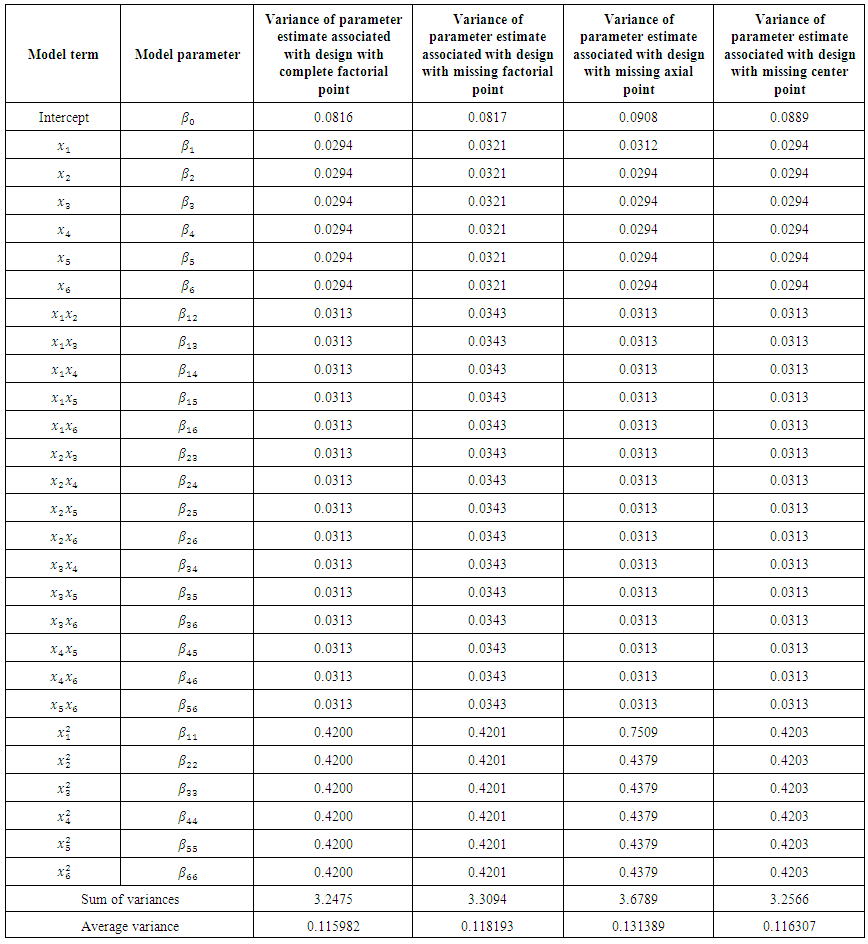 | Table 2. Variances of parameter estimates for the complete and reduced designs (One-half replicate of factorial portion) |
4.3. Six-Factor Central Composite Design with One-Quarter Replicate of Factorial Portion, One Replicate of Axial Portion and Four Replicates of Center Portion
The hat matrix 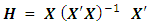 associated with complete cuboidal six-factor central composite design having one-quarter replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix
associated with complete cuboidal six-factor central composite design having one-quarter replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix 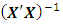 whose elements are as in the immediate.
whose elements are as in the immediate. | Tab. 4.3 |
Trace 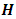 = 28.0000det
= 28.0000det 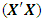 = 2.8145e+024det
= 2.8145e+024det 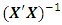 = 3.5530e-025For a missing observation, the 32-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet
= 3.5530e-025For a missing observation, the 32-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet 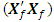 = 1.1806e+021 det
= 1.1806e+021 det 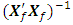 = 8.4703e-022
= 8.4703e-022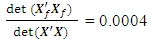 The loss due to missing vertex point is
The loss due to missing vertex point is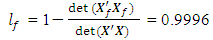 This corresponds to the first entry, 0.9996, of the hat matrix in Appendix C. Associated with a missing axial point is the determinantdet
This corresponds to the first entry, 0.9996, of the hat matrix in Appendix C. Associated with a missing axial point is the determinantdet 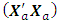 = 7.5558e+022 det
= 7.5558e+022 det 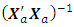 = 1.3235e-023
= 1.3235e-023 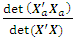 = 0.0268The loss due to missing axial point is
= 0.0268The loss due to missing axial point is 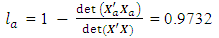 This corresponds to the 65th entry, 0.9732, of the hat matrix in Appendix C. Associated with a missing center point is the determinantdet
This corresponds to the 65th entry, 0.9732, of the hat matrix in Appendix C. Associated with a missing center point is the determinantdet 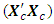 = 2.5831e+024det
= 2.5831e+024det 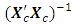 = 3.8713e-025
= 3.8713e-025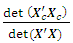 = 0.9178 The loss due to missing center point is
= 0.9178 The loss due to missing center point is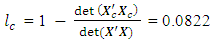 This corresponds to the 80th entry, 0.0822, of the hat matrix in Appendix C.The variances of parameter estimates for the complete and reduced designs are as in Table 3.
This corresponds to the 80th entry, 0.0822, of the hat matrix in Appendix C.The variances of parameter estimates for the complete and reduced designs are as in Table 3. 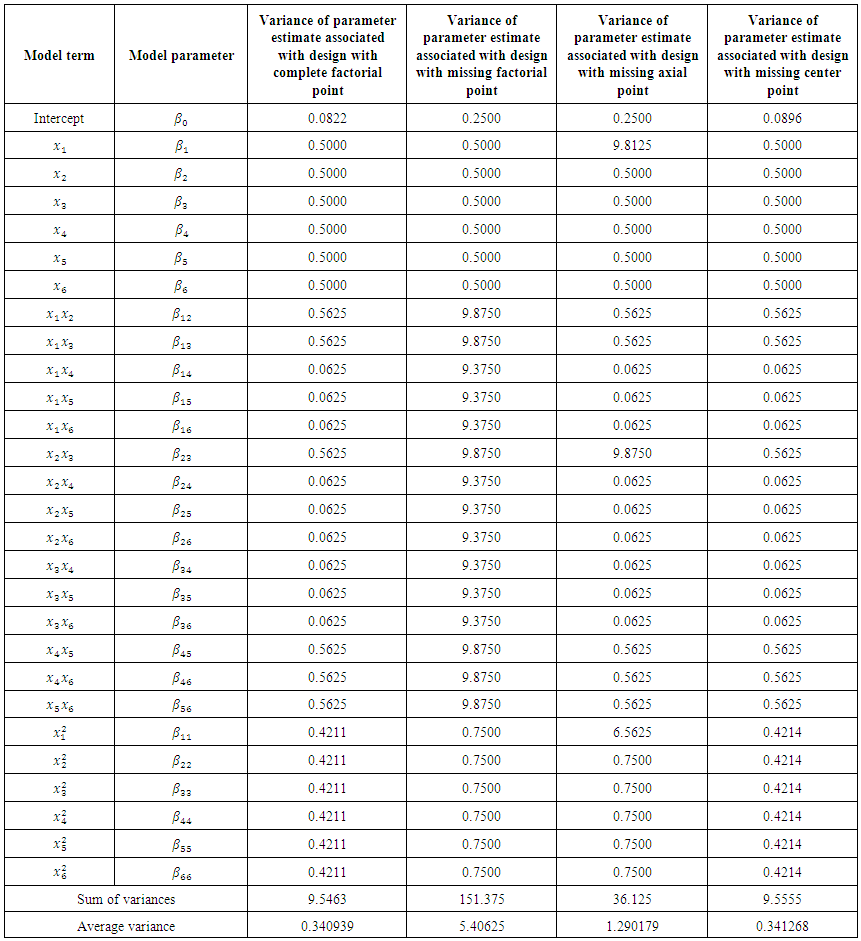 | Table 3. Variances of parameter estimates for the complete and reduced designs (One-quarter replicate) |
5. Discussion of Results
The bahaviours of the hat matrix and the determinant-based loss criterion defined in Akhar and Prescot [2] have been examined for effect of missing observation of six factor central composite design having varying replicates of the factorial portion but fixed replicates of the axial and center portions. It is interesting to note that the hat matrix varies from one deign configuration to another. For the design configuration with one complete replicate of factorial portion, the diagonal entries of the hat matrix associated with a factorial point, an axial point and a center point are respectively 0.3409, 0.4882 and 0.0814. For the design configuration with one-half fractional factorial replicate, the hat matrix remained the same for defining relations I = +ABCDEF and I = −ABCDEF. The diagonal entries of each corresponding hat matrix associated with a factorial point, an axial point and a center point are respectively 0.6764, 0.5025 and 0.0816. For the design configuration with one-quarter fractional factorial replicate, the hat matrix remained the same for defining relations I = +ABC and I = +DEF, I = +ABC and I = −DEF, I = −ABC and I = +DEF and I = −ABC and I = −DEF. The diagonal entries of each corresponding hat matrix associated with a factorial point, an axial point and a center point are respectively 0.9996, 0.9732 and 0.0822. Each of the computed loss value corresponds to the loss computed using the Akhar and Prescot [2] criterion. The loss function, as seen by the three categories of design, is affected by the number of design size, which in this research work is influenced by the number of deign points in the factorial portion.The loss due to missing factorial point is highest when one-quarter fractional factorial makes up the factorial portion of the central composite design and next highest for one-half fractional factorial. The minimum loss due to missing factorial point is attributed to the complete factorial design configuration. The loss due to missing axial point is highest when one-quarter fractional factorial makes up the factorial portion of the central composite design and next highest for one-half fractional factorial. The minimum loss due to missing axial point is attributed to the complete factorial design configuration. The loss due to missing center point is highest when one-quarter fractional factorial makes up the factorial portion of the central composite design and next highest for one-half fractional factorial. The minimum loss due to missing center point is attributed to the complete factorial design configuration. In fact, the loss due to missing center point in the three categories of design is very minimal when compared with loss due to either missing factorial point or missing axial point.There is about 0.25% increase in loss of missing center point when using the design configuration with one-half fractional factorial and about 0.98% increase in loss of missing center point when using the design configuration with one-quarter fractional factorial. There is about 98.42% increase in loss of missing factorial point when using the design configuration with one-half fractional factorial and about 198.22% increase in loss of missing factorial point when using the design configuration with one-quarter fractional factorial. There is about 2.93% increase in loss of missing axial point when using the design configuration with one-half fractional factorial and about 99.34% increase in loss of missing axial point when using the design configuration with one-quarter fractional factorial. It is clearly seen that the configuration with one-quarter fractional factorial attracts higher losses to missing observations of either factorial, axial or center points when compared with either the configuration with one-half fractional factorial or the configuration with complete factorial portion. This result confirms the statement of Ahmad et al. [5] that the effect of missing observations can be much more serious when the design is saturated or near saturated. From characteristics of the design configurations outlined in Table 4, variances associated with parameter estimates are minimum for the design category with complete factorial portion and maximum for the design category with one-quarter fractional factorial. Interestingly, the design category that minimizes the variances also minimizes the losses.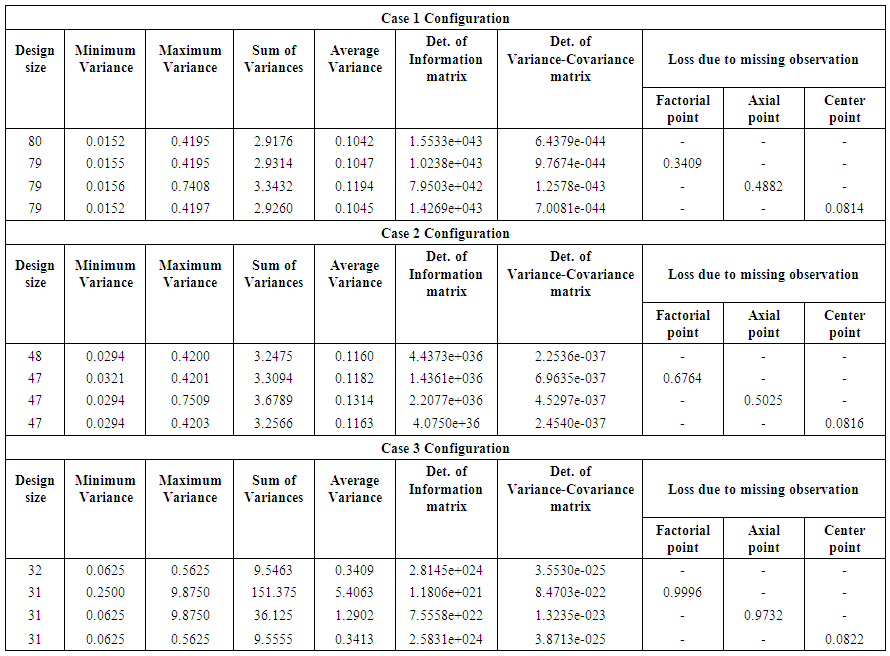 | Table 4. Some characteristics of the design configurations |
Appendix A
 | Hat matrix associated with cuboidal six-factor central composite design with one replicate of factorial portion, one replicate of axial portion and four replicates of center portion |
Appendix B
 | Hat matrix associated with cuboidal six-factor central composite design with one half replicate of factorial portion, one replicate of axial portion and four replicates of center portion |
Appendix C
 | Hat matrix associated with cuboidal six-factor central composite design with one quarter replicate of factorial portion, one replicate of axial portion and four replicates of center portion |
References
| [1] | M. Akhtar, One or two missing observations in five factor Box and Behnken Design, Journal of Engg. & App. Scs, 6 (1) (1987) 87-89. |
| [2] | M. Akhtar, P. Prescott, Response Surface Designs Robust to missing Observations, Communications in Statistics- Simulation, 15 (2) (1986) 245-363. |
| [3] | T. Ahmad, M. Akhtar, Efficient Response Surface Designs for the Second-Order Multivariate Polynomial Model Robust to Missing observation, Journal of Statistical Theory and Practice, 9 (2) (2015) 361-375. |
| [4] | T. Ahmad, S. G. Gilmour, Robustness of subset response surface designs to missing observations, Journal of Statistical Planning and Inference, 140 (1) (2010) 92-103. DOI: 10.1016/j.jspi.2009.06.011. |
| [5] | T. Ahmad, M. Akhtar, S. G. Gilmour, Multilevel Augmented Pairs Second-Order Response Surface Designs and Their Robustness to Missing Data, Communications in Statistics-Theory and Methods, 41 (3) (2011) 437-452. |
| [6] | M. Akhtar, Five-factor Central Composite Designs robust to a pair of missing Observation, Journal of Research (Science), Bahauddin Zakariya University, Multan, Pakistan, 12 (2) (2001) 105-115. |
| [7] | M. Akram, Central Composite Designs Robust to three missing observations, A Ph.D Thesis in Statistics, Islamia University, Bahawalpur (2002). |
| [8] | A. C. Atken, D. E. Rutherford, Determinants and Matrices, Oliver and Boyd Ltd., U. K. (1964). |
| [9] | G. E. P. Box, Non-normality and tests on variances, Biometrika, 40 (3-4) (1953) 318-335. |
| [10] | A. U. Chukwu, Y. Yakubu, T. A. Bamiduro, G. N. Amahia, Robustness of Split-plot Central Composite Designs in the Presence of a Single Missing Observation, The Pacific Journal of Science and Technology, 14 (2) (2013) 194-211. |
| [11] | D. C. Hoaglin, R. E. Welsch, The hat matrix in Regression and ANOVA, The American Statistician, 32 (1) (1978) 17-22. |
| [12] | Myung, W. Kahng, Leverages measures in Nonlinear Regression, Journal of Korean Data & Information Science Society, 18 (1) (2007) 229-235. |
| [13] | E. A. Okon, F. I. Nsude, Central Composite Designs Robust to a pair of Missing Values in Four Factor Experiments, International Journal of Scientific Innovations and Sustainable Development, 5 (1) (2015) 1-11. |
| [14] | B. J., Smucker, W. Jensen, Z. Wu, B. Wang, Robustness of Classical and Optimal Designs to Missing Observations, Computational Statistics & Data Analysis, http://doi.org/10.1016/j.csda.2016.12.001. Available online January 2017, 17 pages. |
| [15] | P. Srisuradetchai, Robust response surface designs against missing observations, A Ph.D dissertation, Montana State University, Bozeman, Montana (2015). |
| [16] | Y. Yakubu, A. U. Chukwu, B. T. Adebayo, A. G. Nwanzo, Effects of missing observations on predictive capability of central composite designs, International Journal on Computational Sciences & Applications, 4 (6) (2014) 1-18. DOI:10.5121/ijcsa.2014.4601. |


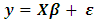
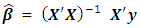 Thus the fitted or estimated value is
Thus the fitted or estimated value is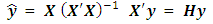
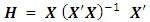 is called the hat matrix and puts the “hat” on the vector of fitted or estimated value. Of course, as a projection matrix, the hat matrix projects y into
is called the hat matrix and puts the “hat” on the vector of fitted or estimated value. Of course, as a projection matrix, the hat matrix projects y into 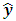 in the model space. In a simpler language, the hat matrix converts values from the observed variable into estimates. In equation (1), y denotes the vector of observations, X denotes the model matrix, β denotes the vector of unknown parameters which are estimated on the basis of N uncorrelated observations and ε denotes the random error component assumed normally and independently distributed with zero mean and constant variance. One major role of the hat matrix in modeling problems is in identifying observations that have greater impacts on the estimation of model parameters and fitted values. Identifying and dealing with such observations help improve statistical inferences. The mention of hat matrix automatically directs one’s mind to leverage which according to Myung and Kahng [12] is one of the basic components of influence in linear regression models. Each diagonal element
in the model space. In a simpler language, the hat matrix converts values from the observed variable into estimates. In equation (1), y denotes the vector of observations, X denotes the model matrix, β denotes the vector of unknown parameters which are estimated on the basis of N uncorrelated observations and ε denotes the random error component assumed normally and independently distributed with zero mean and constant variance. One major role of the hat matrix in modeling problems is in identifying observations that have greater impacts on the estimation of model parameters and fitted values. Identifying and dealing with such observations help improve statistical inferences. The mention of hat matrix automatically directs one’s mind to leverage which according to Myung and Kahng [12] is one of the basic components of influence in linear regression models. Each diagonal element 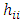 of the hat matrix is called leverage and measures the extent to which the fitted regression model
of the hat matrix is called leverage and measures the extent to which the fitted regression model 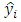 is attracted by the given observation or data point
is attracted by the given observation or data point 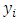 . In essence, the
. In essence, the 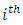 leverage
leverage 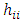 quantifies the influence that the observation
quantifies the influence that the observation 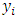 has on its predicted value
has on its predicted value 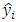 . The diagonal elements of the hat matrix are such that
. The diagonal elements of the hat matrix are such that 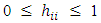 and
and 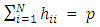 ; where N is the number of data points and p is the number of model parameters, including the intercept. Aside investigating whether one or more observations excessively influence the estimated values, the hat matrix may also be used to quantify the effect of removing one or more observations from a design. Thus, the hat matrix (through its compounds) is useful in understanding effect of alterations to a complete data set. By the alterations, a removed observation is seen as a missing observation. It is desirable to have the effect of missing observations as mild as possible. The term “Robust” first introduced by Box [9] is quite often encountered when studying the effects of missing observations. Akhtar [1] considered the effect of missing observations on the determinant of information matrix. Akhtar [6] considered the effect of missing observations on some configurations of five-factor central composite design and compared the variances of the parameter estimates as well as the sum of variances for each design configuration. Akram [7] assessed the effects of missing observation on the estimates of model parameters. Designs robust to missing observations have been considered by Ahmad and Gilmour [4] and Ahmad et al. [5] using minimax loss criterion. Chukwu et al. [10] considered the robustness of Split-plot central composite designs in the presence of a single missing observation. In their work, minimaxloss criterion, based on D-efficiency, and which accounts for the within-whole plot correlation among the observations, was presented for constructing split-plot response surface designs that are robust to missing a single observation of the various design points. Okon and Nsude [13] investigated alpha values for which the four-factor central composite designs are robust to a pair of missing observations under the minimaxloss criterion. Yakubu et al. [16] considered the impact of single missing observations of the various composite design points on estimation and predictive capability of central composite designs. Some economical designs have been constructed and studied for their robustness to missing data by Ahmad and Akhtar [3]. In studying robust response surface designs against missing observations, Srisuradetchai [15] considered the sensitivity of small second-order designs through the loss of D-efficiency and established the impact of missing observations on predictive variances. Smucker et al. [14] considered the robustness of classical and optimal designs to missing observations using D- and I-efficiencies. Based on recommendation of Akhtar [6] to investigate models with more than five input variables, the effect of a missing observation in six-factor central composite design is considered in this paper. Particular interest is in robustness of fractional replicates of the factorial portion of the six-factor central composite design. Comparison of the effect of a missing observation shall be made using the first compound of the hat matrix.
; where N is the number of data points and p is the number of model parameters, including the intercept. Aside investigating whether one or more observations excessively influence the estimated values, the hat matrix may also be used to quantify the effect of removing one or more observations from a design. Thus, the hat matrix (through its compounds) is useful in understanding effect of alterations to a complete data set. By the alterations, a removed observation is seen as a missing observation. It is desirable to have the effect of missing observations as mild as possible. The term “Robust” first introduced by Box [9] is quite often encountered when studying the effects of missing observations. Akhtar [1] considered the effect of missing observations on the determinant of information matrix. Akhtar [6] considered the effect of missing observations on some configurations of five-factor central composite design and compared the variances of the parameter estimates as well as the sum of variances for each design configuration. Akram [7] assessed the effects of missing observation on the estimates of model parameters. Designs robust to missing observations have been considered by Ahmad and Gilmour [4] and Ahmad et al. [5] using minimax loss criterion. Chukwu et al. [10] considered the robustness of Split-plot central composite designs in the presence of a single missing observation. In their work, minimaxloss criterion, based on D-efficiency, and which accounts for the within-whole plot correlation among the observations, was presented for constructing split-plot response surface designs that are robust to missing a single observation of the various design points. Okon and Nsude [13] investigated alpha values for which the four-factor central composite designs are robust to a pair of missing observations under the minimaxloss criterion. Yakubu et al. [16] considered the impact of single missing observations of the various composite design points on estimation and predictive capability of central composite designs. Some economical designs have been constructed and studied for their robustness to missing data by Ahmad and Akhtar [3]. In studying robust response surface designs against missing observations, Srisuradetchai [15] considered the sensitivity of small second-order designs through the loss of D-efficiency and established the impact of missing observations on predictive variances. Smucker et al. [14] considered the robustness of classical and optimal designs to missing observations using D- and I-efficiencies. Based on recommendation of Akhtar [6] to investigate models with more than five input variables, the effect of a missing observation in six-factor central composite design is considered in this paper. Particular interest is in robustness of fractional replicates of the factorial portion of the six-factor central composite design. Comparison of the effect of a missing observation shall be made using the first compound of the hat matrix.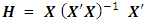 of order N, the mth compound of H is a matrix of order
of order N, the mth compound of H is a matrix of order 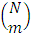 , where N is the number of data points in the complete design and m is the number of missing observations. The mth compound of H is formed by the elements of which are minors of
, where N is the number of data points in the complete design and m is the number of missing observations. The mth compound of H is formed by the elements of which are minors of 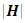 of order m. All possible minors that are
of order m. All possible minors that are 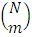 from the same combination of rows (or columns) of H are placed in the same rows (or columns) of the mth compound of H say
from the same combination of rows (or columns) of H are placed in the same rows (or columns) of the mth compound of H say 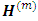 . The elements of
. The elements of 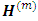 are arranged in lexicographic (or lexical) order. The first compound of the hat matrix is the hat matrix itself. For more on compounds of the hat matrix, see Akram [7] and Atken and Rutherford [8]. In studying the effect of missing observations, Akhar and Prescot [2] defined loss as the relative reduction in the determinant of information matrix associated with the complete design. In this context, a complete design
are arranged in lexicographic (or lexical) order. The first compound of the hat matrix is the hat matrix itself. For more on compounds of the hat matrix, see Akram [7] and Atken and Rutherford [8]. In studying the effect of missing observations, Akhar and Prescot [2] defined loss as the relative reduction in the determinant of information matrix associated with the complete design. In this context, a complete design 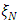 is an N-point design constructed according to response surface model and having no missing data point. A six-factor central composite complete design with full replicate of factorial portion, full replicate of axial portion and four replicates of center portion constructed for a second-order complete model in twenty-eight parameters has eighty data points. The associated design matrix is a matrix of order (80x6). The associated model matrix X is a matrix of order (80x28). The information matrix associated with the complete design is the matrix which is of order (28x28). Generally, an information matrix,
is an N-point design constructed according to response surface model and having no missing data point. A six-factor central composite complete design with full replicate of factorial portion, full replicate of axial portion and four replicates of center portion constructed for a second-order complete model in twenty-eight parameters has eighty data points. The associated design matrix is a matrix of order (80x6). The associated model matrix X is a matrix of order (80x28). The information matrix associated with the complete design is the matrix which is of order (28x28). Generally, an information matrix, 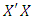 , of a design is a
, of a design is a 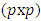 matrix, where p represents the number of model parameters. When an observation or data point in the design is lost or missing, the matrix X reduces by one row. Similarly, when m observations or data points in the design are lost or missing, the matrix X reduces by m rows. As expected, the information matrix, say
matrix, where p represents the number of model parameters. When an observation or data point in the design is lost or missing, the matrix X reduces by one row. Similarly, when m observations or data points in the design are lost or missing, the matrix X reduces by m rows. As expected, the information matrix, say 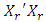 , for the reduced design will be diffierent from the information matrix,
, for the reduced design will be diffierent from the information matrix, 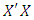 , for the complete design. For (mxp) matrix of m missing rows,
, for the complete design. For (mxp) matrix of m missing rows, 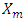 , corresponding to the m missing observations, the complete information matrix may be written as
, corresponding to the m missing observations, the complete information matrix may be written as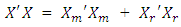
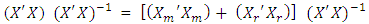
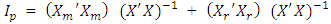 ;
; 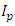 is an identity matrix of order p.By rearrangement we have
is an identity matrix of order p.By rearrangement we have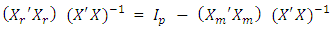
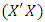 yields
yields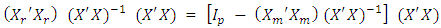
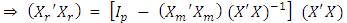
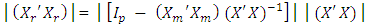
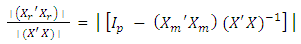
 the diagonal element of the mth compound of (I−H) where H is the hat matrix according to the m missing points and I is an identity matrix of same dimension as H. The loss due to a single missing observation is defined as
the diagonal element of the mth compound of (I−H) where H is the hat matrix according to the m missing points and I is an identity matrix of same dimension as H. The loss due to a single missing observation is defined as 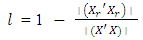
 Using the defining relations I = +ABC and I = +DEF alongside the generalized interaction I = +ABCDEF, the alises of effects under Case 3 are as follows;
Using the defining relations I = +ABC and I = +DEF alongside the generalized interaction I = +ABCDEF, the alises of effects under Case 3 are as follows;
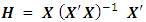 associated with complete cuboidal six-factor central composite design having one replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix
associated with complete cuboidal six-factor central composite design having one replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix 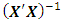 whose elements are as in the immediate.
whose elements are as in the immediate.
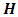 = 28.0000det
= 28.0000det 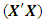 = 1.5533e+043 det
= 1.5533e+043 det 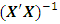 = 6.4379e-044For a missing observation, the 80-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet
= 6.4379e-044For a missing observation, the 80-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet 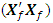 = 1.0238e+043 det
= 1.0238e+043 det 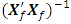 = 9.7674e-044
= 9.7674e-044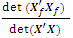 = 0.6591The loss due to missing vertex point is
= 0.6591The loss due to missing vertex point is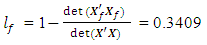 This corresponds to the first entry, 0.3409, of the hat matrix in Appendix A. Associated with a missing axial point is the determinantdet
This corresponds to the first entry, 0.3409, of the hat matrix in Appendix A. Associated with a missing axial point is the determinantdet 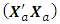 = 7.9503e+042det
= 7.9503e+042det 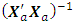 = 1.2578e-043
= 1.2578e-043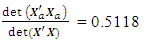 The loss due to missing axial point is
The loss due to missing axial point is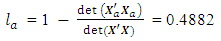 This corresponds to the 65th entry, 0.4882, of the hat matrix in Appendix A. Associated with a missing center point is the determinantdet
This corresponds to the 65th entry, 0.4882, of the hat matrix in Appendix A. Associated with a missing center point is the determinantdet 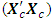 = 1.4269e+043det
= 1.4269e+043det 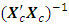 = 7.0081e-044
= 7.0081e-044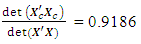 The loss due to missing center point is
The loss due to missing center point is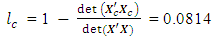 This corresponds to the 80th entry, 0.0814, of the hat matrix in Appendix A.The variances of parameter estimates for the complete and reduced designs are as in Table 1.
This corresponds to the 80th entry, 0.0814, of the hat matrix in Appendix A.The variances of parameter estimates for the complete and reduced designs are as in Table 1. 
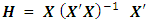 associated with complete cuboidal six-factor central composite design having one-half replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix B. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix
associated with complete cuboidal six-factor central composite design having one-half replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix B. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix 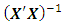 whose elements are as in the immediate.
whose elements are as in the immediate.
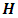 = 28.0000det
= 28.0000det 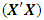 = 4.4373e+036det
= 4.4373e+036det 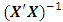 = 2.2536e-037For a missing observation, the 48-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet
= 2.2536e-037For a missing observation, the 48-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet 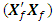 = 1.4361e+036det
= 1.4361e+036det 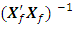 = 6.9635e-037
= 6.9635e-037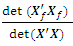 = 0.3236The loss due to missing vertex point is
= 0.3236The loss due to missing vertex point is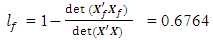 This corresponds to the first entry, 0.6764, of the hat matrix in Appendix B. Associated with a missing axial point is the determinantdet
This corresponds to the first entry, 0.6764, of the hat matrix in Appendix B. Associated with a missing axial point is the determinantdet 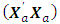 = 2.2077e+036det
= 2.2077e+036det 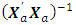 = 4.5297e-037
= 4.5297e-037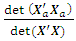 = 0.4975The loss due to missing axial point is
= 0.4975The loss due to missing axial point is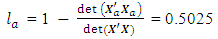 This corresponds to the 65th entry, 0.5025, of the hat matrix in Appendix B. Associated with a missing center point is the determinantdet
This corresponds to the 65th entry, 0.5025, of the hat matrix in Appendix B. Associated with a missing center point is the determinantdet 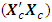 = 4.0750e+036det
= 4.0750e+036det 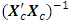 = 2.4540e-037
= 2.4540e-037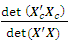 = 0.9184The loss due to missing center point is
= 0.9184The loss due to missing center point is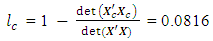 This corresponds to the 80th entry, 0.0816, of the hat matrix in Appendix B.The variances of parameter estimates for the complete and reduced designs are as in Table 2.
This corresponds to the 80th entry, 0.0816, of the hat matrix in Appendix B.The variances of parameter estimates for the complete and reduced designs are as in Table 2. 
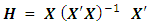 associated with complete cuboidal six-factor central composite design having one-quarter replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix
associated with complete cuboidal six-factor central composite design having one-quarter replicate of factorial portion, one replicate of axial portion and four replicates of center portion is as in Appendix A. The variances and covariances for the model parameter estimates are contained in the variance-covariance matrix 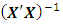 whose elements are as in the immediate.
whose elements are as in the immediate.
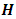 = 28.0000det
= 28.0000det 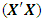 = 2.8145e+024det
= 2.8145e+024det 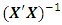 = 3.5530e-025For a missing observation, the 32-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet
= 3.5530e-025For a missing observation, the 32-point design reduces by one observation. A row of the design matrix as well as the model matrix corresponding to the missing observation is deleted. Associated with a missing vertex or factorial point is the determinantdet 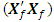 = 1.1806e+021 det
= 1.1806e+021 det 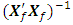 = 8.4703e-022
= 8.4703e-022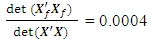 The loss due to missing vertex point is
The loss due to missing vertex point is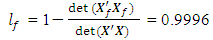 This corresponds to the first entry, 0.9996, of the hat matrix in Appendix C. Associated with a missing axial point is the determinantdet
This corresponds to the first entry, 0.9996, of the hat matrix in Appendix C. Associated with a missing axial point is the determinantdet 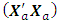 = 7.5558e+022 det
= 7.5558e+022 det 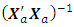 = 1.3235e-023
= 1.3235e-023 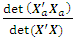 = 0.0268The loss due to missing axial point is
= 0.0268The loss due to missing axial point is 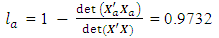 This corresponds to the 65th entry, 0.9732, of the hat matrix in Appendix C. Associated with a missing center point is the determinantdet
This corresponds to the 65th entry, 0.9732, of the hat matrix in Appendix C. Associated with a missing center point is the determinantdet 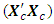 = 2.5831e+024det
= 2.5831e+024det 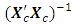 = 3.8713e-025
= 3.8713e-025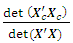 = 0.9178 The loss due to missing center point is
= 0.9178 The loss due to missing center point is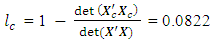 This corresponds to the 80th entry, 0.0822, of the hat matrix in Appendix C.The variances of parameter estimates for the complete and reduced designs are as in Table 3.
This corresponds to the 80th entry, 0.0822, of the hat matrix in Appendix C.The variances of parameter estimates for the complete and reduced designs are as in Table 3. 



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML