-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2017; 7(3): 80-85
doi:10.5923/j.ajcam.20170703.03

A Fuzzy Logic Evaluation of Beliefs and Attitudes of Greek Secondary Teachers about Teaching the Euclidian Geometry
Michael Gr. Voskoglou1, Athena Papadopoulou2
1Department of Applied Mathematics, Graduate Technological Educational Institute of Western Greece, Patras, Greece
2Secondary School Teacher (M. Sc. in Mathematics Education), Patras, Greece
Correspondence to: Michael Gr. Voskoglou, Department of Applied Mathematics, Graduate Technological Educational Institute of Western Greece, Patras, Greece.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A Fuzzy Logic model, based on Triangular Fuzzy Numbers and on the Centre of Gravity defuzzification technique is utilized in this work for evaluating the responses of Greek secondary education teachers on questions about the character of Euclidian Geometry in the school curricula, about the difficulties that they face in communicating with their students when teaching the subject and the nature of these difficulties and about the importance of using the Euclidian Geometry in other mathematical topics taught in secondary schools. These questions were part of a written questionnaire designed by the second author of the present article for the purposes of her M.Sc. dissertation and forwarded to her colleagues for completion. Fuzzy Logic, being closer than Probability and Statistics to our natural language, enabled us here to characterize the teacher responses with linguistic expressions.
Keywords: Euclidian Geometry (EG), Fuzzy Logic (FL), Triangular Fuzzy Numbers (TFNs), Centre of Gravity (COG) Defuzzification Technique
Cite this paper: Michael Gr. Voskoglou, Athena Papadopoulou, A Fuzzy Logic Evaluation of Beliefs and Attitudes of Greek Secondary Teachers about Teaching the Euclidian Geometry, American Journal of Computational and Applied Mathematics , Vol. 7 No. 3, 2017, pp. 80-85. doi: 10.5923/j.ajcam.20170703.03.
Article Outline
1. Introduction
- The introduction of the non Euclidian Geometries by Lobachevsky (1792-1856), Riemann (1826-1866) and others proved, against the existing for centuries opposite view, that our world can be described equally well and it can be explained better (e.g. Einstein’s General Relativity Theory) by using their principles instead of those of the classical Euclidian Geometry (EG). In parallel, the algebraic and analytic methods introduced for Geometry gave genesis to new geometrical topics, like Analytic, Differential and Algebraic Geometry, Topology, etc., which made easier and more effective the study of the geometric properties of curves and surfaces and expanded it to spaces of more than three dimensions. However, it is generally accepted nowadays that the pedagogical value of the EG remains great, mainly because it cultivates the student cognitive skills, it increases their imagination and helps them to understand the usefulness of mathematics by connecting it directly to the real world. However, students face many difficulties for learning the EG, which fluctuate from the understanding of the space to the development of geometric reasoning and the ability of constructing the proofs and solutions of several geometric propositions and problems.Last year (2016), the second author of the present article supported successfully her M.Sc. dissertation [4] submitted to the Department of Mathematics of the University of Patras, in Achaia, Greece. Following a historical review as well as a presentation of the existing theories about the contribution of logic and intuition in mathematical thinking and about the didactical value of EG ([4], pp. 1-34) the main target of that dissertation was to study and analyze views and attitudes of Secondary School teachers about school mathematics in general and about the teaching of the EG in particular. Forty six Mathematics teachers (35 men and 11 women) of various types of Upper High Schools (Lyceum, student age 16-18 years) of the province of Achaia, Greece participated in this study, which was based on their answers to a written questionnaire forwarded to them for completion. The reason of not including Lower High Schools (Gymnasium) at all in the study is well justified by the fact that in those Schools EG is taught in a practical way, not giving any emphasis to theoretical proofs and problems. Therefore, in this way it could not be possible to study the contribution of the EG to the development of critical thinking, which was one of the main objectives of the project. The questionnaire included nineteen in total questions, the first six of them asking anonymously for some personal data (sex, studies, teaching experience, type of school, etc.) for statistical use, eight of them (7-12, 16 and 19) concerning teacher views about secondary mathematics in general and the rest of them (13-15, 17, 18) focusing on the teaching of the EG (Appendix A of [4], pp. 70-78}. The teacher responses were analyzed with the quantitative research methods of the statistical program SPSS 20 (Appendix B of [4], pp. 79-99). A qualitative analysis also followed for some special teacher responses corresponding to certain questions of open type, like, for example, Question 16, where the teachers were aked where they based their didactic approach in general ([4], pp. 63-67). Among others, the author analyzed: 1. The role of the teacher in a modern class of Mathematics. 2. The difficulties faced by the students during the teaching of EG. 3. The contribution of EG to the development of mathematical thinking. From the data processing it was shown that there were different views among the teachers, even within the same school, expressing interesting approaches and attitudes on the teaching of the EG. The perception about the pedagogical value of EG was reinforced in general by the outcomes of this study, a fact which creates an impulse for further research on the subject and in a more general context on the modern approaches of teaching and learning Mathematics.Here we shall focus only on the questions concerning the teaching of the EG. Among those, Question 18 was asking if the teachers use any kind of software for teaching the EG and the possible answers were: “Geogebra”, “Sketchpad”, “Gabri”, “Other” and “None”. For the rest of the questions of this category, the second author of this article and designer of the questionnaire, in her will to give to her colleagues the comfort to express unbiased their views, used fuzzy linguistic labels for characterizing their possible answers. For example, in Question 13 about the character of the EG in the school curricula, the possible answers to be chosen by the participants were: “Dynamic”, “Satisfactory”, “Deficient” and “Negligible”, etc. (for more details see Section 3).Note that situations appear frequently in education characterized by a degree of uncertainty and/or ambiguity. A teacher, for example, is not many times sure about the exact numerical grade corresponding to a student’s performance or about the degree of understanding of a new topic by students, etc. Fuzzy Logic (FL), due to its property of characterizing real life situations with multiple values (yes, no, may be, very possible, enough or less possible, etc.), offers rich resources for manipulating such kind of ambiguous / uncertain situations. This gave several times in past the impulse to the first author of the present article to use principles of FL as tools for describing or assessing such kind of situations in education, and not only, like learning a subject matter, problem solving and mathematical modelling, analogical and more generally case-based reasoning (CBR), decision-making, etc. (e.g. see [7-13] among his many works on this subject).The target of the present article is to use Triangular Fuzzy Numbers (TFNs) as tools for evaluating the outcomes of dissertation [4] on the teaching of the EG in Greek secondary schools. The rest of the article is formulated as follows: In Section 2 a model is developed utilizing TFNs as assessment tools, while in Section 3 this model is applied for evaluating the outcomes of Questions 13-15 and 17 of the above mentioned questionnaire. The last Section 4 contains our conclusions and some hints for further research.
2. Utilizing Triangular Fuzzy Numbers (TFNs) as Assessment Tools
- For general facts on Fuzzy Sets (FSs) and Fuzzy Numbers (FNs), which are special forms of FSs on the set R of real numbers, we refer to the books [3] and [2] respectively. In particular, for the concepts of the Triangular FNs (TFNs), of the sum of two TFNs, of the scalar product of a TFN with a positive real number and of the mean value of a finite number of given TFNs, which will be used in this work, we refer to Definitions 3, 5-7 of [10] and to Definition 7 of [11]. Also, it is well known that the coordinates (X, Y) of the Centre of Gravity (COG) of the graph of a TFN (a, b, c), being the COG G of the triangle ABC of Figure 1, are calculated by the formulas:
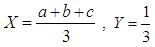 | (1) |
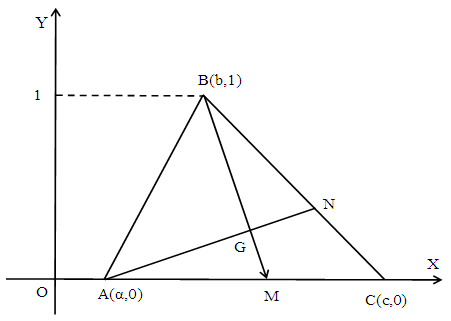 | Figure 1. COG of the graph of the TFN (a, b, c) |
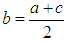 | (2) |
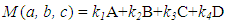 be a TFN, with ki non negative real numbers, i=1, 2, 3, 4. Then the x-coordinate of the COG of the graph of M is equal to
be a TFN, with ki non negative real numbers, i=1, 2, 3, 4. Then the x-coordinate of the COG of the graph of M is equal to 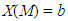 Proof: If M is one of the TFNs A, B, C, D, then combining equalities (1) and (2) one finds that
Proof: If M is one of the TFNs A, B, C, D, then combining equalities (1) and (2) one finds that 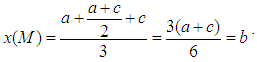 In general, if A (a1, b1, c1), B (a2, b2, c2), C (a3, b3, c3), D(a4, b4, c4) and M(a, b, c), then
In general, if A (a1, b1, c1), B (a2, b2, c2), C (a3, b3, c3), D(a4, b4, c4) and M(a, b, c), then 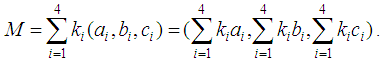 Therefore,
Therefore, 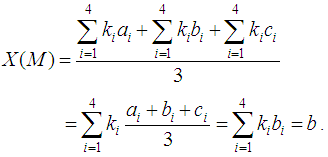 Remark 1: An alternative way for defuzzifying a TFN T = (a, b, c) is to use the Yager Index Ya (T), introduced in [14] in terms of the a-cuts of T, with a in [0, 1], in order to help the ordering of fuzzy sets. It can be shown ([5], p. 62) that
Remark 1: An alternative way for defuzzifying a TFN T = (a, b, c) is to use the Yager Index Ya (T), introduced in [14] in terms of the a-cuts of T, with a in [0, 1], in order to help the ordering of fuzzy sets. It can be shown ([5], p. 62) that 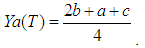 Observe now that
Observe now that 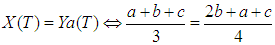
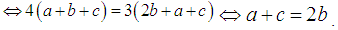 The last equality is not true in general for a<b<c; e.g. take a=1, b=2.5 and c=3. In other words we have in general that
The last equality is not true in general for a<b<c; e.g. take a=1, b=2.5 and c=3. In other words we have in general that 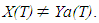 Nevertheless, by (2) the above equality holds for the TFNs A, B, C, and D, therefore it obviously holds also for any linear combination of those TFNs. Thus, the above two defuzzification techniques provide the same outcomes when used in the previously developed assessment model with TFNs.
Nevertheless, by (2) the above equality holds for the TFNs A, B, C, and D, therefore it obviously holds also for any linear combination of those TFNs. Thus, the above two defuzzification techniques provide the same outcomes when used in the previously developed assessment model with TFNs. 3. Fuzzy Assessment of the Greek Secondary Teacher Views about the EG
- As said in our Introduction, here we shall focus on Questions 13-15 and 17 only of the second author’s questionnaire (see Appendix A of [4]). Each of these questions will be treated separately, as follows:Question 13: How do you evaluate the character of the EG in the secondary school curricula?Possible answers to choose: A= dynamic, B= satisfactory, C = deficient, D = negligibleTeacher answers: A=0, B=14, C=31, D=1Percentages: A=0, B
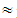 30.44, C
30.44, C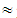 67.39, D
67.39, D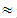 2.17Mean value of TFNs:
2.17Mean value of TFNs: Therefore, by Proposition 1, X(M)
Therefore, by Proposition 1, X(M) 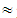 64.07, showing that the character of the EG in secondary school curricula was characterized by the teachers as deficient. Observe that, while the statistical outcomes give the percentages of the several teacher answers, the fuzzy outcomes give a general characterization of these answers.Question 14: Do you face difficulties in communicating with your students when teaching EG?Possible answers to choose: A= very many, B= many, C = enough, D = noneTeacher answers: A= 8, B=23, C= 14, D=1Percentages: A
64.07, showing that the character of the EG in secondary school curricula was characterized by the teachers as deficient. Observe that, while the statistical outcomes give the percentages of the several teacher answers, the fuzzy outcomes give a general characterization of these answers.Question 14: Do you face difficulties in communicating with your students when teaching EG?Possible answers to choose: A= very many, B= many, C = enough, D = noneTeacher answers: A= 8, B=23, C= 14, D=1Percentages: A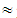 17.39, B=50, C
17.39, B=50, C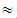 30.44, D
30.44, D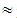 2.17Mean value of TFNs:
2.17Mean value of TFNs: X(M)
X(M) 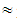 73.23. Therefore teachers face many difficulties in communicating with their students during the teaching of the EG.Question 15: According to your opinion what causes the difficulties related to Question 14:i) The student little contact with EG?ii) The student cognitive vacuums from their previous years at school?iii) The non use of supervisory teaching means?iv)The deficient teacher information on the use of the new technologies in education?v) The nature of EG?vi) The little time available for teaching the subject ?Possible answers to choose: A= very much, B= enough, C = a little, D = not at all.Teacher answers:i) A= 7, B=25, C= 10, D=4ii) A= 13, B=29, C= 4, D=0iii) A= 5, B=11, C= 20, D=10iv) A= 1, B=6, C= 19, D=20v) A= 8, B=20, C= 13, D=5vi) A= 18, B=20, C= 8, D=0Percentages:i) A
73.23. Therefore teachers face many difficulties in communicating with their students during the teaching of the EG.Question 15: According to your opinion what causes the difficulties related to Question 14:i) The student little contact with EG?ii) The student cognitive vacuums from their previous years at school?iii) The non use of supervisory teaching means?iv)The deficient teacher information on the use of the new technologies in education?v) The nature of EG?vi) The little time available for teaching the subject ?Possible answers to choose: A= very much, B= enough, C = a little, D = not at all.Teacher answers:i) A= 7, B=25, C= 10, D=4ii) A= 13, B=29, C= 4, D=0iii) A= 5, B=11, C= 20, D=10iv) A= 1, B=6, C= 19, D=20v) A= 8, B=20, C= 13, D=5vi) A= 18, B=20, C= 8, D=0Percentages:i) A 15.21, B
15.21, B 54.35, C
54.35, C 21.74, D
21.74, D 8.70ii) A
8.70ii) A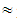 28.26, B
28.26, B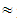 63.04, C
63.04, C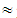 8.70, D=0iii) A
8.70, D=0iii) A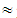 10.87, B
10.87, B 23.91, C
23.91, C 43.48, D
43.48, D 21.74iv) A
21.74iv) A 2.17, B
2.17, B 13.05, C
13.05, C 41.30, D
41.30, D 43.48v) A
43.48v) A 17.39, B
17.39, B 43.48, C
43.48, C 28.26, D
28.26, D 10.87vi) A
10.87vi) A 39.13, B
39.13, B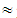 43.48, C
43.48, C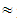 17.39, D=0Mean values of TFNs:i) M1 =
17.39, D=0Mean values of TFNs:i) M1 = 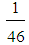 (7A+25B+10C+4D) =
(7A+25B+10C+4D) =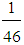 (2845, 3265.5, 3686)
(2845, 3265.5, 3686) 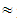 (61.85, 70.99, 80.13),X(M1)
(61.85, 70.99, 80.13),X(M1) 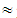 70.99 (enough)ii) M2 =
70.99 (enough)ii) M2 = 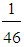 (13A+29B+4C+0D) =
(13A+29B+4C+0D) =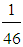 (3335, 3673.5, 4012)
(3335, 3673.5, 4012) 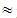 (72.5, 79.86, 87.22),X(M2)
(72.5, 79.86, 87.22),X(M2) 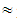 79.86 (enough)iii) M3 =
79.86 (enough)iii) M3 = 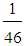 (5A+11B+20C+10D) =
(5A+11B+20C+10D) =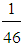 (2195, 2744.5, 3294)
(2195, 2744.5, 3294) 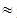 (47.72, 59.66, 71.61),X(M3)
(47.72, 59.66, 71.61),X(M3) 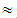 59.66 (a little)iv) M4 =
59.66 (a little)iv) M4 = 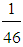 (1A+6B+19C+20D) =
(1A+6B+19C+20D) =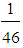 (1455, 2175, 2895)
(1455, 2175, 2895) 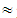 (31.63, 47.28, 62.93),X(M4)
(31.63, 47.28, 62.93),X(M4) 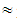 47.28 (not at all)v) M5 =
47.28 (not at all)v) M5 = 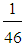 (8A+20B+13C+5D) =
(8A+20B+13C+5D) =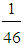 (2730, 3176, 3622))
(2730, 3176, 3622)) 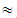 (59.35, 69.05, 78.74),X(M5)
(59.35, 69.05, 78.74),X(M5) 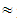 69.04 (a little to enough)vi) M6 =
69.04 (a little to enough)vi) M6 = 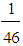 (18A+20B+8C+0D) =
(18A+20B+8C+0D) =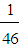 (3330, 3681, 4032))
(3330, 3681, 4032)) 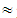 (72.39, 80.02, 87.65),X(M6)
(72.39, 80.02, 87.65),X(M6) 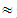 80.72 (very much).Therefore, according to the teacher opinions, the luck of time for teaching the EG causes very many difficulties, followed by the student cognitive vacuums and their little contact to the subject causing enough difficulties. Further, the nature of EG causes little to enough difficulties, the non use of supervisory means causes little difficulties, while the deficient teacher information about the use of the new technologies in education does not seem to cause any considerable difficulties.The mean value of all the above mean values (cases i - vi) is equal to
80.72 (very much).Therefore, according to the teacher opinions, the luck of time for teaching the EG causes very many difficulties, followed by the student cognitive vacuums and their little contact to the subject causing enough difficulties. Further, the nature of EG causes little to enough difficulties, the non use of supervisory means causes little difficulties, while the deficient teacher information about the use of the new technologies in education does not seem to cause any considerable difficulties.The mean value of all the above mean values (cases i - vi) is equal to with X(M*)
with X(M*)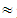 67.81, showing that all the above reasons cause as a total little difficulties to the teachers in communicating with their students during the teaching of EG. This suggests that, apart from those stamped in the statement of Question 15, other reasons could possibly exist causing the many difficulties indicated by the teacher responses to Question 14.Question 17: How important do you consider the use of EG in the other mathematical topics taught in secondary schools, like Algebra, Differential and Integral Calculus, etc. ?Possible answers to choose: A= very much, B= enough, C = very little, D = not at allTeacher answers: A= 19, B=26, C= 1, D=0Percentages: A
67.81, showing that all the above reasons cause as a total little difficulties to the teachers in communicating with their students during the teaching of EG. This suggests that, apart from those stamped in the statement of Question 15, other reasons could possibly exist causing the many difficulties indicated by the teacher responses to Question 14.Question 17: How important do you consider the use of EG in the other mathematical topics taught in secondary schools, like Algebra, Differential and Integral Calculus, etc. ?Possible answers to choose: A= very much, B= enough, C = very little, D = not at allTeacher answers: A= 19, B=26, C= 1, D=0Percentages: A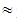 41.30, B
41.30, B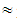 56.53, C
56.53, C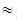 2.17, D=0Mean value of TFNs:
2.17, D=0Mean value of TFNs: X(M)
X(M) 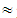 83.02 (very much).Remark 2: In cases where the individual performance of each member of a certain group is characterized by a numerical score (grade), e.g. from 0-100, the traditional method of assessing the group’s mean performance is the calculation of the mean value of those scores. Nevertheless, in the above case study (Questions 13 – 15, 17) the “performance” (actually response) of each member of the given group (secondary teachers) is characterized by a linguistic expression (A, B, C, D) only and not with a numerical score, which means that the calculation of the mean value is not applicable. In such cases our fuzzy method with the TFNs is really useful, providing a satisfactory approximation of the group’s mean “performance” (actually the teachers’ behaviour in our case study).To illustrate this, let us reconsider, for example, the teachers’ answers to Question 17 under two extreme scenarios: In the first scenario the maximal possible numerical score is attached to each teacher’s response and in the second scenario the minimal one. The above two scenarios correspond to the mean values
83.02 (very much).Remark 2: In cases where the individual performance of each member of a certain group is characterized by a numerical score (grade), e.g. from 0-100, the traditional method of assessing the group’s mean performance is the calculation of the mean value of those scores. Nevertheless, in the above case study (Questions 13 – 15, 17) the “performance” (actually response) of each member of the given group (secondary teachers) is characterized by a linguistic expression (A, B, C, D) only and not with a numerical score, which means that the calculation of the mean value is not applicable. In such cases our fuzzy method with the TFNs is really useful, providing a satisfactory approximation of the group’s mean “performance” (actually the teachers’ behaviour in our case study).To illustrate this, let us reconsider, for example, the teachers’ answers to Question 17 under two extreme scenarios: In the first scenario the maximal possible numerical score is attached to each teacher’s response and in the second scenario the minimal one. The above two scenarios correspond to the mean values 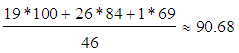 and
and 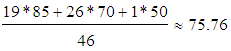 respectively.Observe now that
respectively.Observe now that 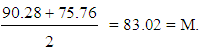 Therefore the mean value M determined by using the TFNs is equal to the mean value of the above two extreme scenarios.Remark 3: Another traditional assessment method of a group’s overall performance is the calculation of the Grade Point Average (GPA) index. It is recalled here that the GPA index is a weighted average obtained by assigning greater coefficients to the higher scores. More explicitly, GPA =
Therefore the mean value M determined by using the TFNs is equal to the mean value of the above two extreme scenarios.Remark 3: Another traditional assessment method of a group’s overall performance is the calculation of the Grade Point Average (GPA) index. It is recalled here that the GPA index is a weighted average obtained by assigning greater coefficients to the higher scores. More explicitly, GPA =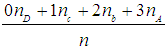 , where
, where 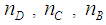 and
and 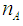 denote the numbers of the elements of the group which obtained the grades D, C, B, A respectively and n denotes the total number of its elements [12]. Therefore, the GPA index, in contrast to the mean value, focuses on the group’s quality performance.In the ideal case (nA = n) the above formula gives GPA = 3, while in the worst case (nD = n) it gives GPA = 0. Therefore, values of GPA greater than
denote the numbers of the elements of the group which obtained the grades D, C, B, A respectively and n denotes the total number of its elements [12]. Therefore, the GPA index, in contrast to the mean value, focuses on the group’s quality performance.In the ideal case (nA = n) the above formula gives GPA = 3, while in the worst case (nD = n) it gives GPA = 0. Therefore, values of GPA greater than 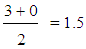 could be considered as demonstrating a more than satisfactory performance.In case of Question 17 one finds that GPA =
could be considered as demonstrating a more than satisfactory performance.In case of Question 17 one finds that GPA =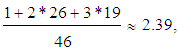 corresponding to an importance considerably greater than the medium one. Nevertheless, since GPA is focused on the group’s quality performance, the value of M found above by using the TFNs gives a more representative overall view of the teachers’ responses to Question 17.Remark 4: The reason of choosing to work with TFNs in this article is because they are the simplest form of FNs, in which the usual arithmetic operations can be easily performed, making the calculation of their mean value a simple process. However, other forms of FNs could be also used for assessment purposes.For example, Trapezoidal Fuzzy Numbers (TpFNs) have been introduced in ([9], Section 4) for assessing basket-ball player performance. But, the model with the TpFNs developed in [9, 10] is applicable when the performance of each member, say P, of the group under assessment is evaluated by a numerical score, say s, lying in a subinterval [a1, b1] of [0, 100]. Consequently a1 and b1 are numerical scores assigned to the fuzzy labels, say Q and T, which are equal to one (the same or different) of the fuzzy labels A, B, C, D. Then, we choose P to be equal to the TpFN (a, a1, b1, b), where a is the lower numerical score assigned to Q and b is the upper numerical score assigned to T. For example, if s lies in the interval [73, 87], then Q = C and T = A, therefore P = (60, 73, 87, 100). The mean value of all those TpFNs ([10], Definition 7), can be also considered then as a representative measure for assessing the group’s mean performance.However, since in the above case study (Questions 13, 15-17) the teacher responses are evaluated by using linguistic characterizations only, the above conditions do not hold and therefore the assessment model with the TpFNs is not applicable. But, even if the teacher responses were evaluated by numerical scores, since each response should be represented by a different TpFN and the number of teachers (46) is large enough, the calculation of their mean value would be laborious and therefore difficult to be applied in practice without the help of a calculator.
corresponding to an importance considerably greater than the medium one. Nevertheless, since GPA is focused on the group’s quality performance, the value of M found above by using the TFNs gives a more representative overall view of the teachers’ responses to Question 17.Remark 4: The reason of choosing to work with TFNs in this article is because they are the simplest form of FNs, in which the usual arithmetic operations can be easily performed, making the calculation of their mean value a simple process. However, other forms of FNs could be also used for assessment purposes.For example, Trapezoidal Fuzzy Numbers (TpFNs) have been introduced in ([9], Section 4) for assessing basket-ball player performance. But, the model with the TpFNs developed in [9, 10] is applicable when the performance of each member, say P, of the group under assessment is evaluated by a numerical score, say s, lying in a subinterval [a1, b1] of [0, 100]. Consequently a1 and b1 are numerical scores assigned to the fuzzy labels, say Q and T, which are equal to one (the same or different) of the fuzzy labels A, B, C, D. Then, we choose P to be equal to the TpFN (a, a1, b1, b), where a is the lower numerical score assigned to Q and b is the upper numerical score assigned to T. For example, if s lies in the interval [73, 87], then Q = C and T = A, therefore P = (60, 73, 87, 100). The mean value of all those TpFNs ([10], Definition 7), can be also considered then as a representative measure for assessing the group’s mean performance.However, since in the above case study (Questions 13, 15-17) the teacher responses are evaluated by using linguistic characterizations only, the above conditions do not hold and therefore the assessment model with the TpFNs is not applicable. But, even if the teacher responses were evaluated by numerical scores, since each response should be represented by a different TpFN and the number of teachers (46) is large enough, the calculation of their mean value would be laborious and therefore difficult to be applied in practice without the help of a calculator.4. Discussion and Conclusions
- In the article at hands Greek secondary teacher responses were evaluated by using TFNs as assessment tools and the COG defuzzification technique It is important to notice that the use of FL, which is closer to our natural language than Probability and Statistics, enabled us to give a general linguistic characterization to the teacher responses in each question. For example, the character of EG in the secondary school curricula was characterized as deficient, the use of the EG in other mathematical topics taught in secondary schools was found to be too important, the teacher difficulties in communicating with their students during the teaching of EG were explored to be many, etc.The evaluation model with TFNs used in this work has a general character, which means that, in parallel with the already developed analogous model using Trapezoidal Fuzzy Numbers (TpFNs) [9, 10], can be used for assessing any kind of human (e.g. student progress, player or athlete performance, reasoning skills, etc.) or machine (e.g. CBR or decision-making computer systems) activities, e.g. see [7-13], etc. This is a very promising area for further future research and in particular the comparison of those two assessment methods (TFNs / TpFNs), in cases where they are applicable, to each other for listing their advantages and disadvantages, as well as their comparison with other existing assessment methods of the classical logic (mean values, GPA index [12], information content [1], etc.) and of the FL (measurement of uncertainty, COG technique and its variations, etc. [7-13]).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML