Fahad B. Mostafa, MA Samad, MR Hossain
Department of Applied Mathematics, University of Dhaka, Bangladesh
Correspondence to: Fahad B. Mostafa, Department of Applied Mathematics, University of Dhaka, Bangladesh.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Day by day research of non-Newtonian fluids is increasing because of its huge existence in the universe. Applications of non-Newtonian fluids in many industrial implementations have been an interesting topic to many researchers. Atmospheric elements, bio fluids such as blood, multiphase mixers, pharmaceutical formulation, cosmetics and toiletries, paints, and beverage items are examples of non-Newtonian fluids. Through this study, an analysis has been carried out to study the combined effect of unsteady free convection boundary layer flow of non-Newtonian fluid along a vertically stretched surface with viscous dissipation and thermal radiation in the presence of magnetic field. The governing nonlinear partial differential equations have been transformed to dimensionless equations with the help of similarity consideration to determine similarity solutions. Transformed equations have been discretized by implicit finite difference approximation to get solutions. The result of non-dimensional velocity and temperature profiles are depicted and discussed for different parameter such as Prandtl number Pr, Eckert number Ec, magnetic parameter M, and radiation parameter N. Moreover, for scientific interest the effects of skin friction coefficient (Cf) and Nusselt number (Nu) are presented in tables.
Keywords:
Unsteady non-Newtonian fluid, Variable thermal conductivity, Thermal radiation, Heat transfer, Natural convection, Viscous dissipation
Cite this paper: Fahad B. Mostafa, MA Samad, MR Hossain, Combined Effect of Viscous Dissipation and Radiation on Unsteady Free Convective Non-Newtonian Fluid Along a Continuously Moving Vertically Stretched Surface with No-Slip Phenomena, American Journal of Computational and Applied Mathematics , Vol. 7 No. 3, 2017, pp. 71-79. doi: 10.5923/j.ajcam.20170703.02.
1. Introduction
Since the study of non-Newtonian fluid flow has become an important matter for the applicants. Schowalter [1] and [2] was the first who observed the formula of boundary layer flow of a Non-Newtonian fluid as well as the similarity solution which is a significant process for solving most of the fluid mechanics problem in recent time. Elbashbeshy [3] found heat transfer over a stretching surface with variable and uniform surface heat flux subject to injection and suction. Sakiadis [4] and [5] was the first who analyze the boundary layer flow on a continuous moving solid surface in a Newtonian fluid. Later, it was studied by Crane [6], who had gained an exact solution of the boundary-layer flow of the Newtonian fluid caused by the stretching of an elastic sheet moving in its own plane linearly. For various applications in industry, the study of non-Newtonian fluid flow and heat transfer over a stretched surface gets significant attention. These kinds of fluid exhibit non linier relationship between shear stress and rate of strain such as polymer solutions, molten plastics, paints and foods. Chamkha [7] also studied radiation effects on free convection flow past a semi-infinite vertical plate. Raptis and Perdikis [8] analyzed radiation and free convection flow past a moving plate. Nuclear power plants, satellites, space vehicles, and submarines are interest of such engineering areas. In case of high temperature the interaction of radiation with hydro-magnetic flow has become industrially more noticeable. Kishan and Sashidha Reddy [9] were studied the momentum and heat transfer in laminar boundary layer flow of non- Newtonian fluids past a semi-infinite flat plates with the thermal dispersion in the presence of a uniform magnetic field for both the cases of static plate and continuous moving plate. At present time, the radiation effect on MHD flow and heat transfer problems has become more significant industrially. Effects of radiation on non-Newtonian fluids have been studied by many researchers Mansour and Gorla [10]. Moreover, the study of viscous dissipation has been interestingly increased for decreasing the waste of energy. The effect of viscous dissipation and pressure stress work on free convection flow along a vertical flat plate has been investigated by Alam, Alim and Chowdhury [11]. B.K. Jha and A.O. Ajibade [12] studied the Effect of viscous dissipation on natural convection flow between vertical plates with time period boundary conditions. Recently, viscous dissipation Effect on Natural Convection Flow along a vertically wavy surface has been studied by Parveen et al. [13]. A. Shahzad, R Ali [14] & [15] investigated the power law fluid over a vertical stretching street with the convective boundary condition for MHD flows. Furthermore, approximate analytic solution has been studied. M. Khan et al. [16] analysed on Falken-Skan flow with mixed convection. J Ahmed et al. [17] studied on boundary layer flow of Sisko fluid over a radially stretching sheet where Lorentz forces are effective. A Shahzad et al. [18] investigated the unsteady case for axisymmetric flow and heat transfer over time-dependent radially stretching sheet. J Ahmed et al. [19] also studied Axis symmetrical flow and heat transfer over an unsteady stretching sheet for power law fluid. Saha et al. [20] investigated the effect of viscous dissipation on MHD free convection flow heat and mass transfer of non-Newtonian fluids along a continuously moving stretching sheet. In this present investigation, combined effect of viscous dissipation and radiation on unsteady non-Newtonian fluid along a vertically stretched surface has been investigated. In this work, flow has been discussed for free convection and no-slip condition. The similarity transformation is used to transform the governing equations into dimensionless equations and Finite Difference Method has been used to obtain approximate solutions. Finally the study has been compared with Chen, C.H. [21] to obtain standard verifications.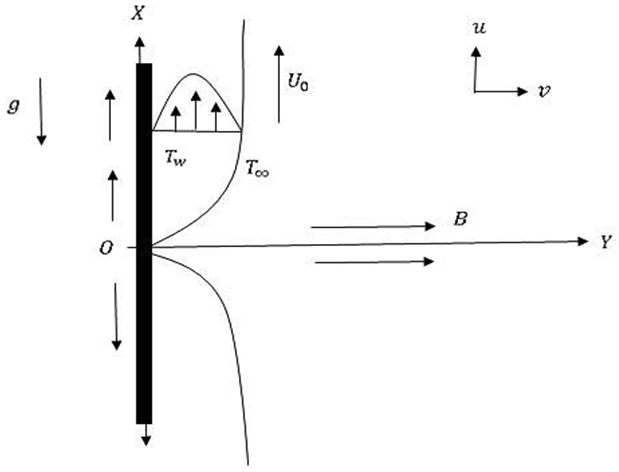 | Figure 2.1. Physical model of plate |
2. Formulation
We consider the unsteady free convection laminar boundary layer flow of a non-Newtonian fluid along a stretching surface in the vertical direction which is moving continuously. We also assume the combined effect of viscous dissipation and radiation for this particular study. Boundary layer development has been generalized by the existence of zero velocity at the surface of the plate. For this particular study, the velocity component 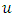 of
of  axis pertains along the surface and the
axis pertains along the surface and the  of
of 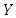 axis normal to the surface of the sheet. Two equal and opposite forces are performed to keep the origin fixed for
axis normal to the surface of the sheet. Two equal and opposite forces are performed to keep the origin fixed for 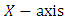 so that the sheet is stretched. The power law is used to describe fluid behavior, permit mathematical predictions, and correlate computerized experimental data in this case.
so that the sheet is stretched. The power law is used to describe fluid behavior, permit mathematical predictions, and correlate computerized experimental data in this case.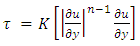 | (1) |
If the surface and flow temperature differs, there will be a region where the fluid temperature varies from, 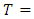
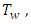 at
at 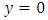 to
to 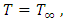 at
at 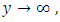 in the flow of outer region. This region is known as thermal boundary layer. Suppose, no change of temperature profiles of the surface
in the flow of outer region. This region is known as thermal boundary layer. Suppose, no change of temperature profiles of the surface 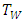 as well as the free stream temperature profile
as well as the free stream temperature profile 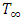 are taken respectively. For natural convection the flow is induced by a force known as buoyancy forces, which arise from density
are taken respectively. For natural convection the flow is induced by a force known as buoyancy forces, which arise from density 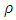 differences caused by the variation of temperature in the region. If we go through molecular level of the fluid, it shows us the changes of temperature profiles such as
differences caused by the variation of temperature in the region. If we go through molecular level of the fluid, it shows us the changes of temperature profiles such as 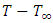 is arisen by the different values of temperature of the fluid particle. The relative change is calculated as
is arisen by the different values of temperature of the fluid particle. The relative change is calculated as 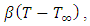 where
where 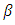 is designated as the volumetric coefficient of thermal expansion. Gravitational force is involved because of buoyancy force. In this case,
is designated as the volumetric coefficient of thermal expansion. Gravitational force is involved because of buoyancy force. In this case, 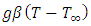 is the lift force per unit volume where gravitational acceleration
is the lift force per unit volume where gravitational acceleration 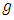 is working through vertical axis. Hence,
is working through vertical axis. Hence, 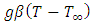 is active at
is active at 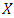 dirction.
dirction. 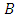 is used as applied magnetic field which is reliable on fluid’s characters. But it causes the growth of magnetic force
is used as applied magnetic field which is reliable on fluid’s characters. But it causes the growth of magnetic force 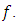
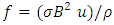 To describe this discrete mathematical problem let us formulate the governing equations as follows:
To describe this discrete mathematical problem let us formulate the governing equations as follows: 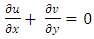 | (2) |
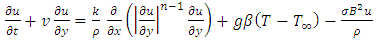 | (3) |
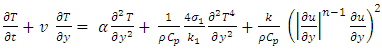 | (4) |
Initial conditions: 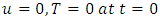 and Boundary conditions:
and Boundary conditions: 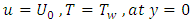 and
and 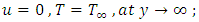 for
for 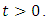

3. Similarity Consideration
Introducing 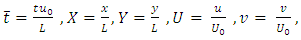
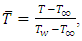 Where L is the characteristic length and
Where L is the characteristic length and 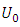 is an arbitrary reference velocity which is related to this problem. Since free stream conditions are quiescent in free convection, there is no logical external reference velocity
is an arbitrary reference velocity which is related to this problem. Since free stream conditions are quiescent in free convection, there is no logical external reference velocity 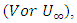 as in forced convection. The radiative heat flux
as in forced convection. The radiative heat flux 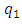 is described by the Rosseland approximation such that,
is described by the Rosseland approximation such that, 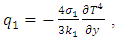 Note that Rosseland approximation is valid for optically thick fluids.
Note that Rosseland approximation is valid for optically thick fluids. 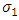 is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and 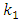 is the Rosseland mean absorption coefficient. It is surmised that the temperature difference within the flow is sufficiently small such that that
is the Rosseland mean absorption coefficient. It is surmised that the temperature difference within the flow is sufficiently small such that that 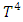 can be can be expressed in the Taylor series, where free stream temperature
can be can be expressed in the Taylor series, where free stream temperature 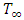 and neglecting the higher order terms from Taylor series expansion
and neglecting the higher order terms from Taylor series expansion 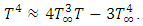 Therefore,
Therefore, 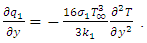 So, the dimensionless momentum equation and ultimate dimensionless energy equation are:
So, the dimensionless momentum equation and ultimate dimensionless energy equation are: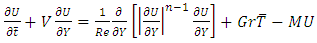 | (5) |
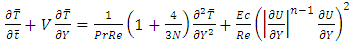 | (6) |
Initial condition at 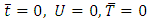 and Boundary condition at
and Boundary condition at 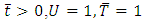 when
when 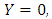
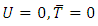 when
when 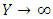 . (7) Where, the radiation number
. (7) Where, the radiation number 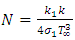 , Reynolds number
, Reynolds number 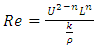 , Prandlt Number
, Prandlt Number 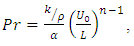 Eckert number
Eckert number 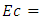
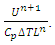 Here the modified version of dimensionless numbers are used. Note that, those numbers are valid for this fluid flow only. It may appear different in different flows.
Here the modified version of dimensionless numbers are used. Note that, those numbers are valid for this fluid flow only. It may appear different in different flows.
4. Numerical Computation
Although several procedures are available for solving such equations, the solutions typically involve complicated mathematical series and functions and may be obtained for only a set of simple geometries and boundary condition. We will use implicit finite difference technique to approximate the solution of governing equations. Finally we will discuss its convergences. Rectangular region of the flow field is chosen, the region is divided into a grid of lines parallel to 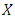 and
and 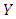 axes, where
axes, where 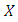 is chosen along the stretching surface and
is chosen along the stretching surface and 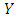 is normal to the plate.
is normal to the plate. 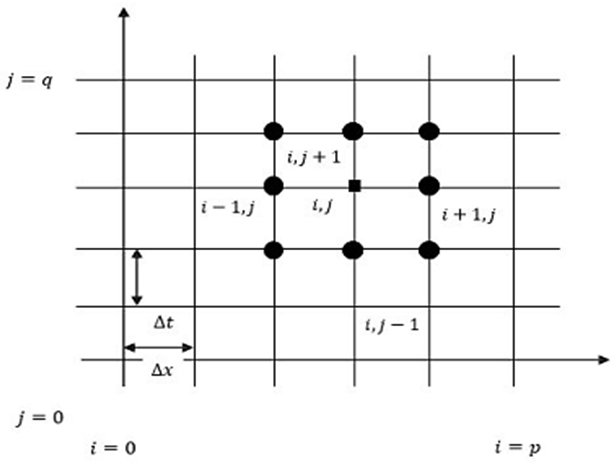 | Figure 4.1. Numerical model |
Let assume the length of the sheet is 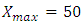 which indicates that x varies from 0 to 50 where
which indicates that x varies from 0 to 50 where 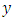 varies for 0 to
varies for 0 to  So the step size is calculated below.Here
So the step size is calculated below.Here 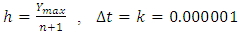 and for grid spacing
and for grid spacing 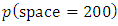 and
and 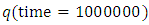 in the
in the 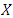 and
and 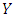 directions respectively.Two point forward difference formula for determining time derivatives, two point central difference method has chosen to approximate the space involving derivatives and three point central difference approximation to find double derivative. Now the equations (5) to (7) becomes:
directions respectively.Two point forward difference formula for determining time derivatives, two point central difference method has chosen to approximate the space involving derivatives and three point central difference approximation to find double derivative. Now the equations (5) to (7) becomes: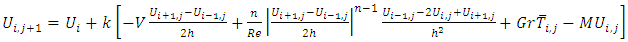 | (7) |
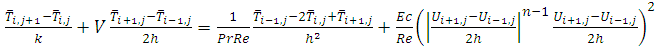 | (8) |
for 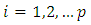 and
and 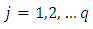 Initial condition at
Initial condition at 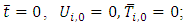 Boundary condition at
Boundary condition at 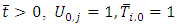
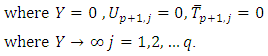 | (9) |
The skin friction coefficient is, 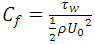 and the Nusselt number is,
and the Nusselt number is, 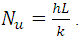 Using FDM the discretize equations are
Using FDM the discretize equations are 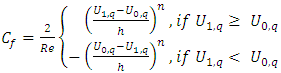 and
and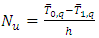 | (10) |
5. Results and Explanations
The updated velocity profile 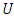 and temperature profile
and temperature profile 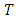 are obtained at all internal node points by successive application of the equations (7) to (9). The whole process will be done again and again and used time step will be sufficiently small. Effects of dimensionless numbers on velocity and temperature has been depicted through graphs. Using (10) skin friction coefficients and Nusselt numbers are obtained then solutions are shown in the table.From the Figure 5.1 the velocity profile decreases with the increase of magnetic parameter M in each type of fluid. It has been obtained that, introducing magnetic field in the flow causes higher restriction to the fluid. For Newtonian and pseudo plastic fluid the velocity profile reduces in same rate but in case of dilatant fluid rate of reduction is little bit slower. Thus, velocity profile decreases as
are obtained at all internal node points by successive application of the equations (7) to (9). The whole process will be done again and again and used time step will be sufficiently small. Effects of dimensionless numbers on velocity and temperature has been depicted through graphs. Using (10) skin friction coefficients and Nusselt numbers are obtained then solutions are shown in the table.From the Figure 5.1 the velocity profile decreases with the increase of magnetic parameter M in each type of fluid. It has been obtained that, introducing magnetic field in the flow causes higher restriction to the fluid. For Newtonian and pseudo plastic fluid the velocity profile reduces in same rate but in case of dilatant fluid rate of reduction is little bit slower. Thus, velocity profile decreases as 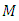 increases in all types of fluids which reduces faster for Newtonian fluid compared to non-Newtonian fluids. But in case of temperature profile there is no significant effect found.
increases in all types of fluids which reduces faster for Newtonian fluid compared to non-Newtonian fluids. But in case of temperature profile there is no significant effect found.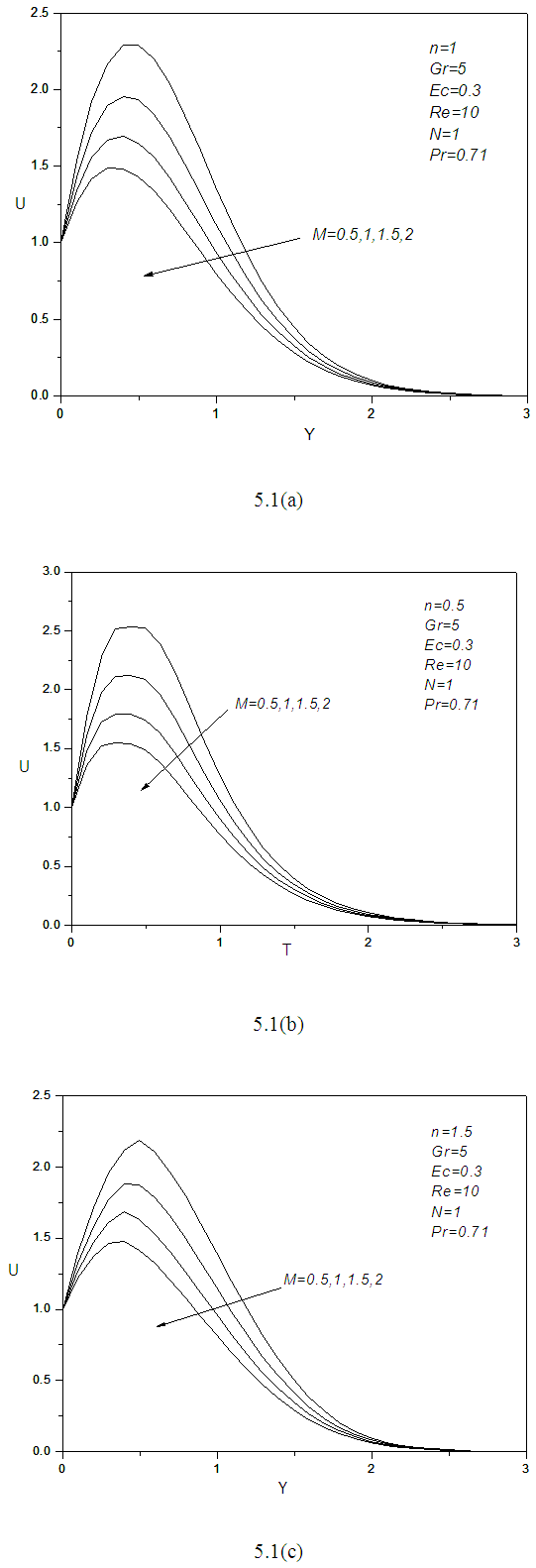 | Figure 5.1. (a, b, c): effect of Magnetic parameter M on velocity profile for different values of n |
It is distinct from Figure 5.2 that velocity profile U decreases with the increase of radiation parameter N. However the rate of decreasing is almost same at the beginning of the surface but at the point 0.3 of Y scale. It is also clear that the momentum boundary layer thickness reduces rapidly for decreasing N. For small changes of N such as 0.5 to 1 the rate of decreasing velocity is about 0.94% for n=1,0.77% for n=1.5 and 0.25% for n=0.5 respectively. But if the changes of radiation parameter is from 1 to 2, then reducing rate decreases because of free convection. However in case of free convection we cannot think huge radiation from the fluid.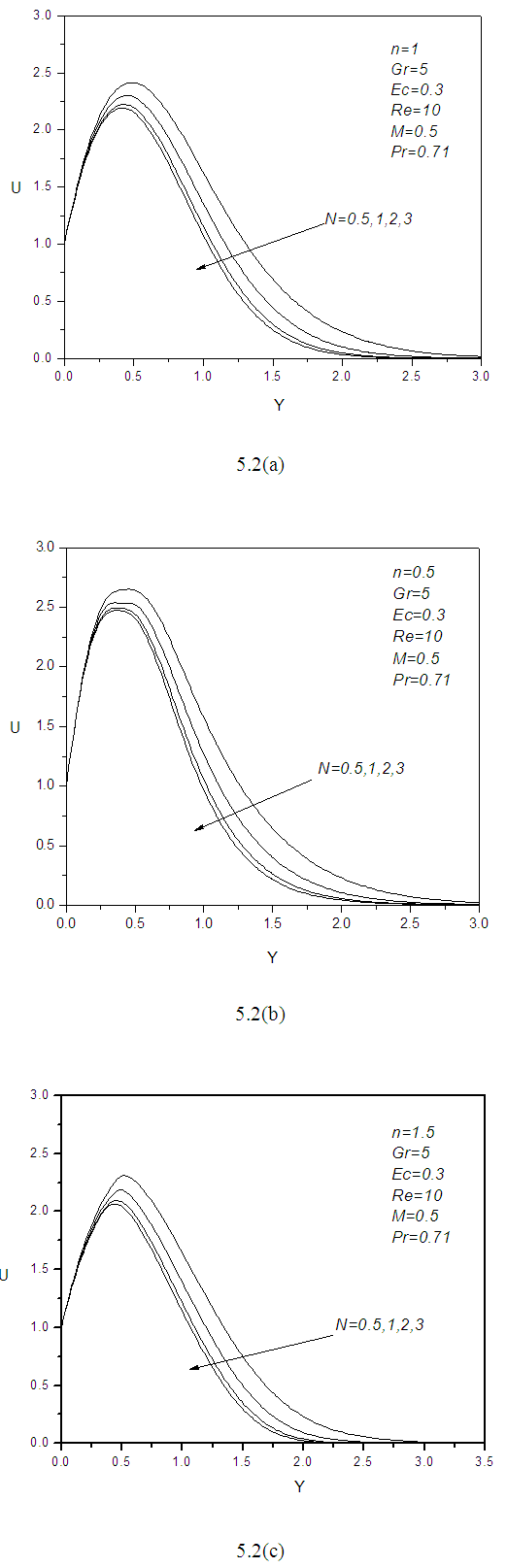 | Figure 5.2. (a, b, c): effect of Radiation parameter N on velocity profile for different values of n |
According to the above Figure 5.3 the temperature profile decreases with in positive increment of the magnitude of radiation parameter 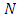 . Form above result, we observe that the small increment cause a lot to the thermal boundary layer. Temperature profile reduces to zero slowly. So from the above illustration it is evident that numerical outcomes support the physical experiment (Newton’s law of cooling). The rate of heat transfer is thus increased. So we can use the effect of radiation to control the velocity and temperature of boundary layer.
. Form above result, we observe that the small increment cause a lot to the thermal boundary layer. Temperature profile reduces to zero slowly. So from the above illustration it is evident that numerical outcomes support the physical experiment (Newton’s law of cooling). The rate of heat transfer is thus increased. So we can use the effect of radiation to control the velocity and temperature of boundary layer.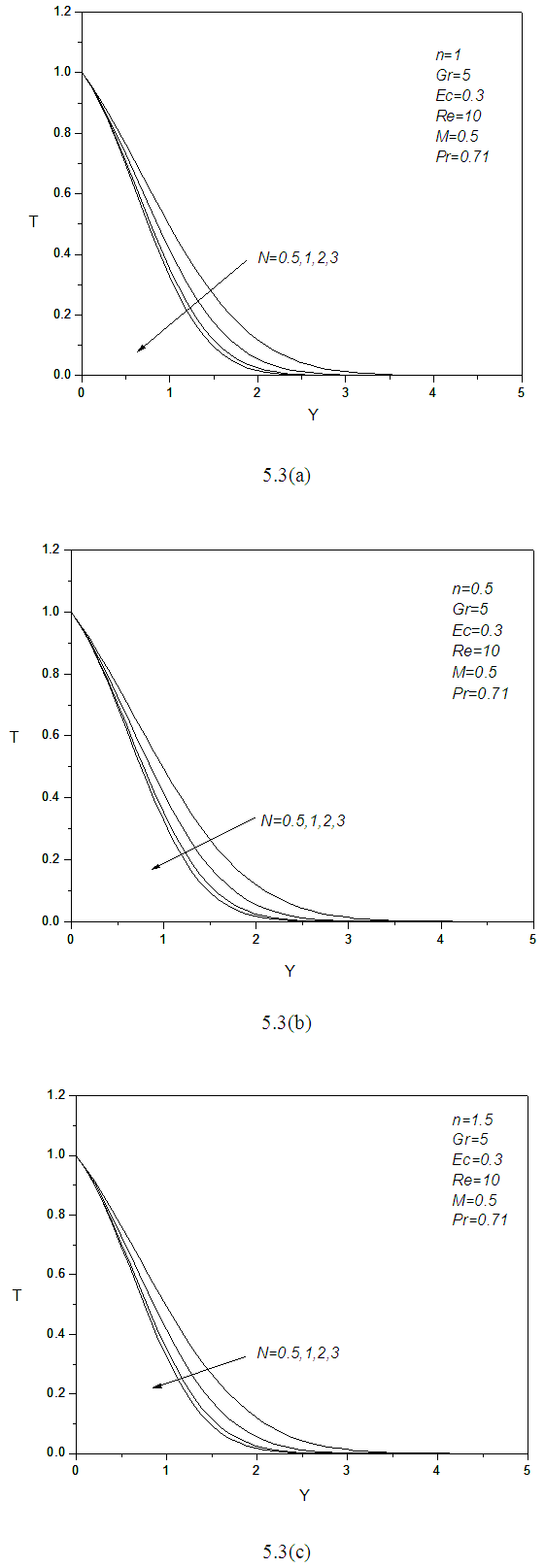 | Figure 5.3. (a, b, c): effect of Radiation parameter N on temperature profile for different values of n |
Figure 5.4 shows the effect of Prandtl number 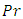 on velocity profile shows significant changes for the increase of its magnitude. From the figure it can be told the rate of reduction is little for three types of fluid for large Prandtl number but for small Prandtl number such as
on velocity profile shows significant changes for the increase of its magnitude. From the figure it can be told the rate of reduction is little for three types of fluid for large Prandtl number but for small Prandtl number such as 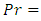
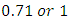 the reduction rate is larger. However for
the reduction rate is larger. However for 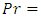
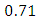 there is a sharp rise in the velocity boundary layers near stretching surface. Physically
there is a sharp rise in the velocity boundary layers near stretching surface. Physically 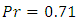 corresponds to air and
corresponds to air and 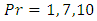 is for different values of water. For pseudo plastic fluid the velocity profile rise higher and slowly decreases to zero at the wall.
is for different values of water. For pseudo plastic fluid the velocity profile rise higher and slowly decreases to zero at the wall.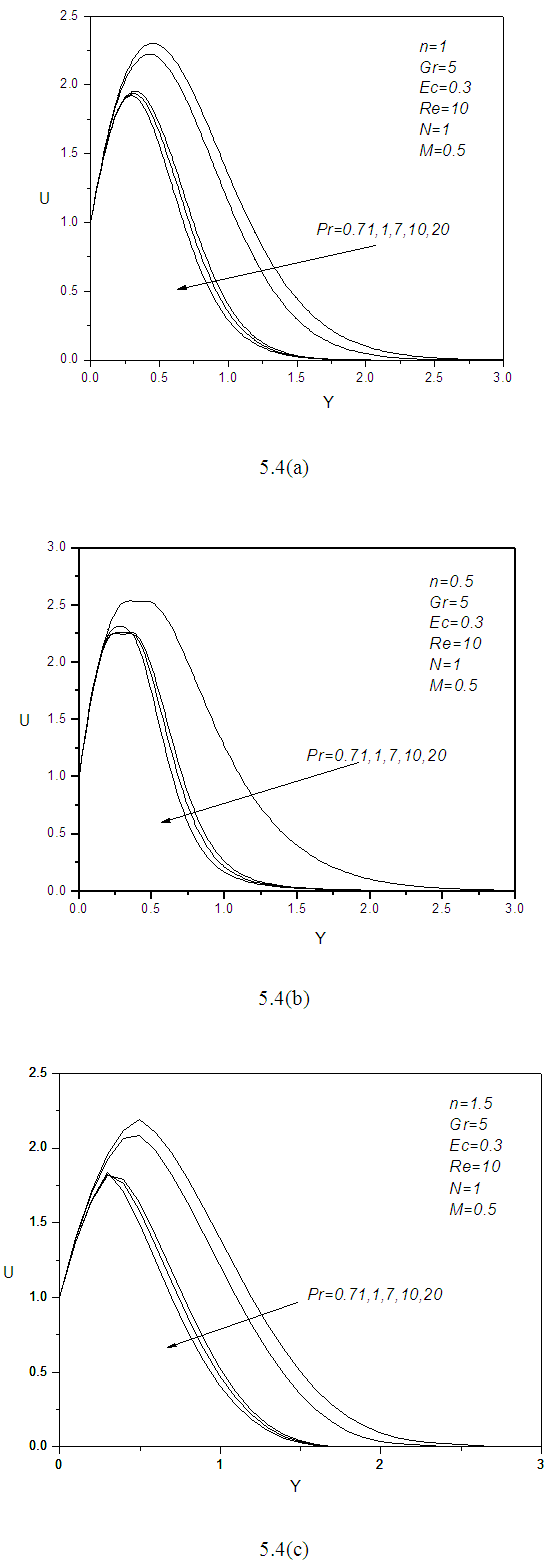 | Figure 5.4. (a, b, c): effect of Prandtl number Pr on velocity profile for different values of n |
It is clear from Figure 5.5 that for small Prandtl number the temperature profile reduces to zero at the wall with the increase of 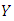 steps. But when
steps. But when 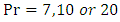 then profiles raises a little at the beginning and then slowly reduces to zero at the wall. The rate of reduction is almost same for these three types of fluid. Moreover, cross flows have been found for each case.
then profiles raises a little at the beginning and then slowly reduces to zero at the wall. The rate of reduction is almost same for these three types of fluid. Moreover, cross flows have been found for each case.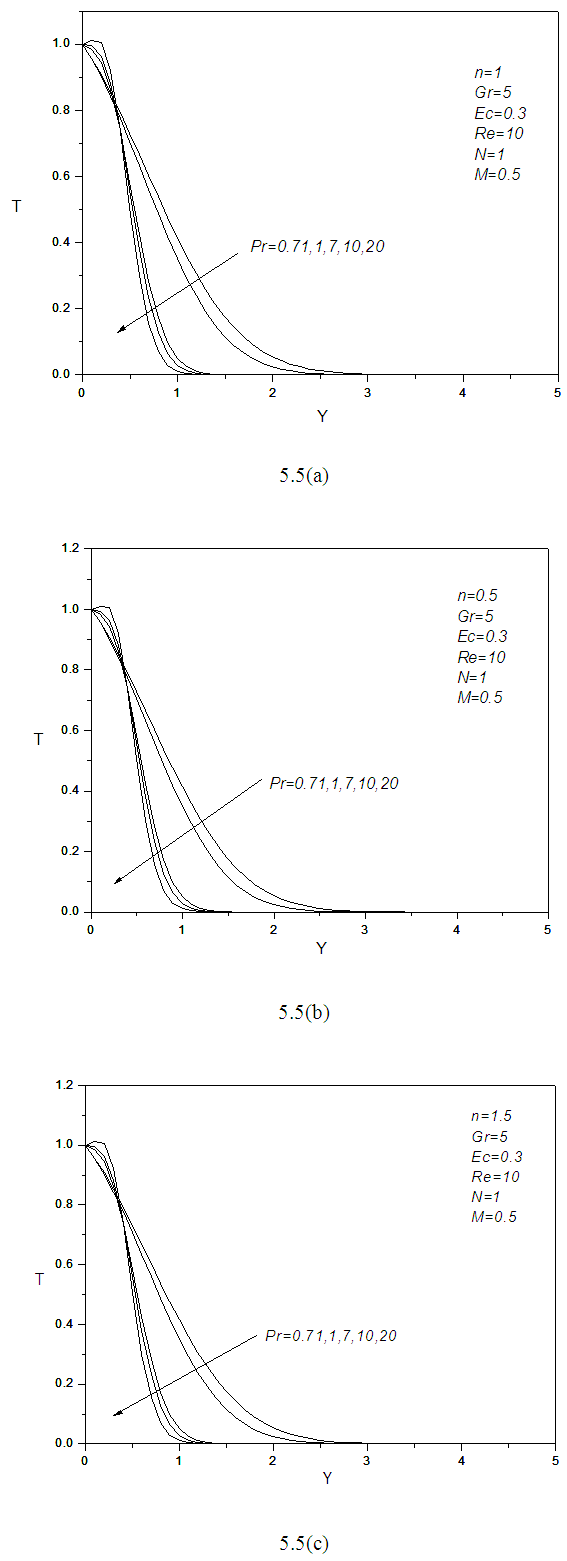 | Figure 5.5. (a, b, c): effect of Prandtl number Pr on temperature profile for different values of n |
Figure 5.6: According to Eckert number it implies the ratio of advective transport and heat dissipation potential. It provides the connection between a flow's kinetic energy and the boundary layer enthalpy difference, and is used to characterize heat dissipation. Ec number shows small effect on velocity and temperature profile for its small changes. For Newtonian fluid the Figure 4.9, peaks of the velocity profile are just over 2.25 of velocity scale where in case pseudo plastic fluid it is almost 2.5 but for dilatant fluid it is just under 2.25 of velocity scale. All these velocity profile increases at the beginning and slowly fall to zero with the increment of Y steps. The rate of increment of velocity and temperature profile with the increase of Eckert number Ec are almost same. For each type of fluid momentum boundary layer thickness and thermal boundary layer thickness have changed over the increment of Ec.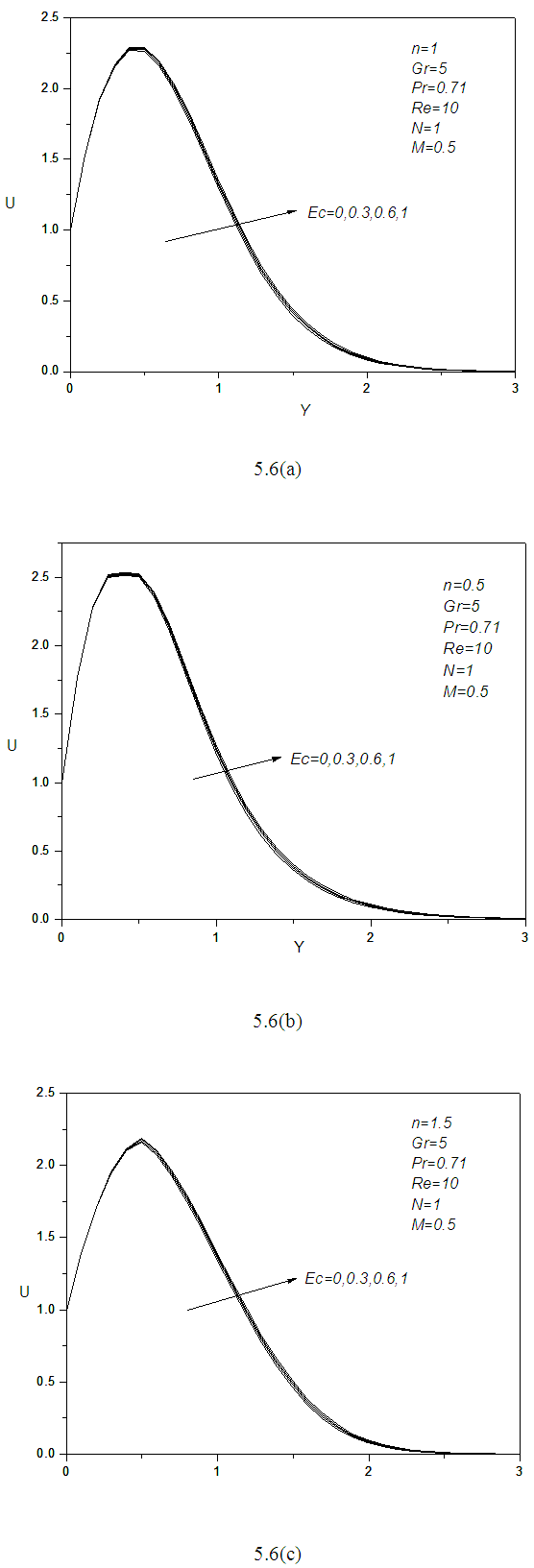 | Figure 5.6. (a, b, c): effect of Eckert number Ec on velocity profile for different values of n |
From Figure 5.7 it reveals there are not any significant changes of temperature profiles T at the beginning and at the end for different values of Ec. But at the mid-point of each profile it shows its variation. Although the rate of change is very small and profile slowly rises for the increment of Ec.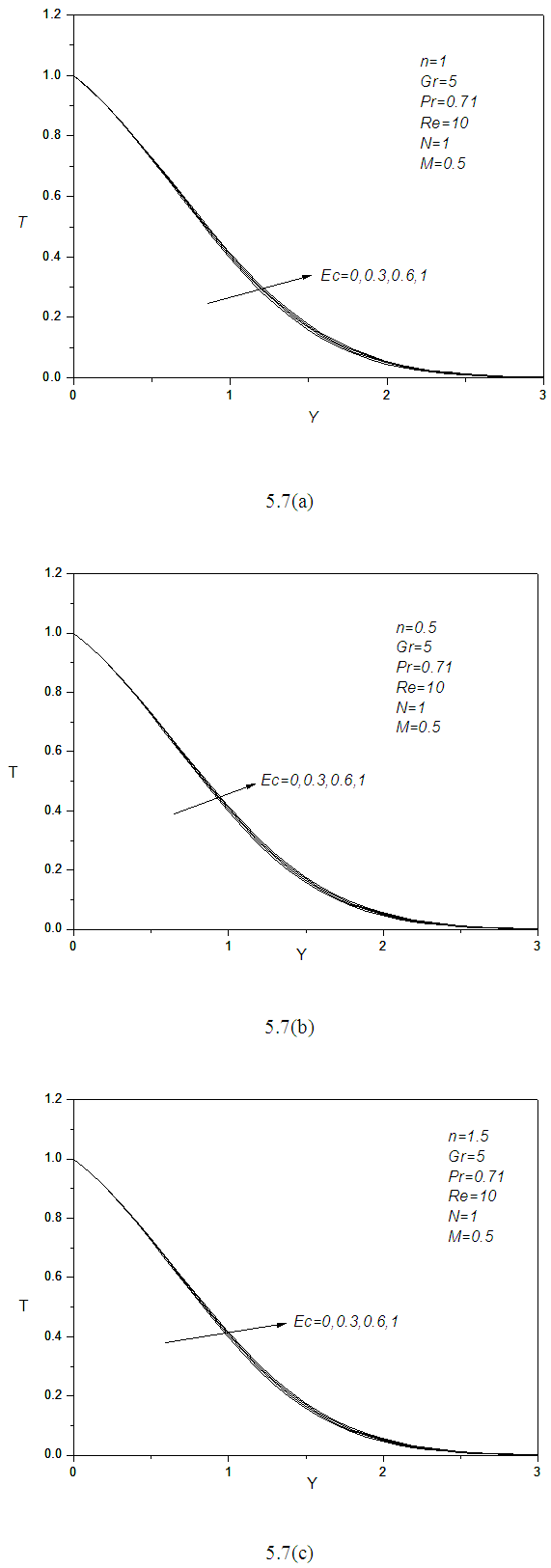 | Figure 5.7. (a, b, c): effect of Eckert number Ec on temperature profile for different values of n |
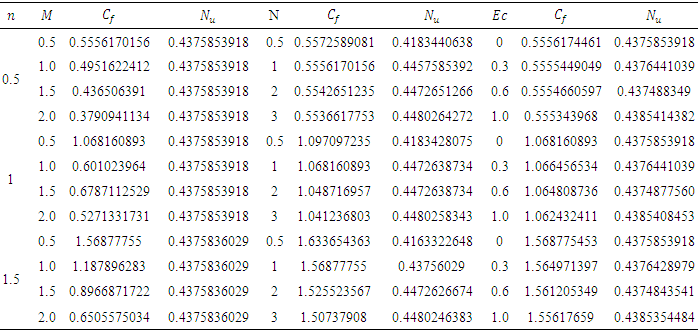
From the table 5.7 it indicates 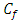 reduces with the increment of
reduces with the increment of 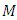 but
but 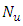 remain unchanged.
remain unchanged. 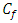 and
and 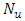 decreased significantly for the increase of
decreased significantly for the increase of 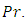 In this case cross flow has been found.
In this case cross flow has been found. 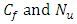 shows opposite scenario. Where skin friction increases slowly and Nusselt number decreases, although the effect is very small. Thermal radiation can be used to control the boundary layer. Skin friction coefficient
shows opposite scenario. Where skin friction increases slowly and Nusselt number decreases, although the effect is very small. Thermal radiation can be used to control the boundary layer. Skin friction coefficient 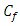 has decreased slowly but Nusselt number
has decreased slowly but Nusselt number 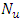 effect shows diversity for the increase of N in case of different power law index n.To show the validity of the model described above, skin friction coefficient as well as heat transfer rate have been calculated and compared to the Chen (2008) model for specific parameter.
effect shows diversity for the increase of N in case of different power law index n.To show the validity of the model described above, skin friction coefficient as well as heat transfer rate have been calculated and compared to the Chen (2008) model for specific parameter. Table 5.1. Skin friction coefficient (Cf) and Nusselt number (Nu) for different n, M, N, Ec
 |
| |
|
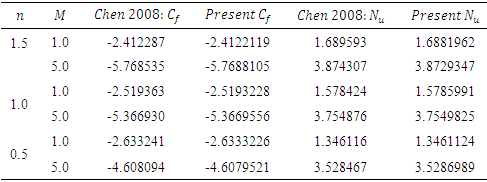
Table 5.2. Comparison table for Skin friction coefficient Cf and Nusselt number Nu excluding unsteady term, viscous dissipation and radiation term for free convection
 |
| |
|
6. Conclusions
Ÿ To control the velocity and thermal boundary layer, thermal radiation can be used significantly.Ÿ Wall friction has been increased due to buoyancy force which has thicken the boundary layer.Ÿ The heat transfer rate has been increased by absolving thermal energy from the surface.Ÿ Drag of pseudo-plastic fluid along a vertically stretched surface has been decreased as velocity profile increased.Ÿ A strong magnetic field can be applied to increase the wall temperature of the pseudo-plastic fluids.Ÿ Cross flow has been found for variation of Prandtl number.Ÿ Eckert number shows small effect. 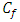 decreased but
decreased but 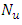 has increased with the growth of
has increased with the growth of 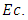
ACKNOWLEDGEMENTS
Authors gratefully acknowledges to the Ministry of National Science and Technology Bangladesh and the Department of Applied Mathematics of Dhaka University.
References
| [1] | Schowalter, W.R.: The application of boundary layer theory to power-law pseudo plastic fluid Similar solutions, AICHE J. 6, 24-28 (1960). |
| [2] | Schowalter W.R.: Mechanics of Non-Newtonian Fluids, Pergamon Press, Oxford, (1978). |
| [3] | Elbashbeshy, E.M.A.: Heat transfer over a stretching surface with variable surface heat flux, J. Phys. D Appl. Phys. 31, 1951-1954. (1998). |
| [4] | Sakiadis. B.C.: Boundary-layer behavior on continuous solid surface on a continuous flat surface-I, The boundary layer on a continuous flat surface, AICHE J. 7, 26-28(1961a). |
| [5] | Sakiadis. B.C.: Boundary-layer behavior on continuous solid surface on a continuous flat surface-II, The boundary layer on a continuous flat surface, AICHE J. 7, 221-225 (1961b). |
| [6] | Crane, L. J.: Flow Past a Stretching Plate, ZAMP. 21, 645-647(1970). |
| [7] | Chamkha, A.J., Takhar H.S. and Soundalgekar V.M.: Radiation effect on free convection flow past a semi-Infinite vertical plate with mass transfer. Chem. Eng. J. 84, 335-342 (2001). |
| [8] | Raptis, A. and Perdikis C.: Radiation and free convection flow past a moving plate. App. Mech. Eng. 4, 817-821(1999). |
| [9] | Kishan Naikoti, Shashidar Reddy Borra.: Quasi-linearization Approach to MHD Effects on Boundary Layer Flow of Power-Law Fluids Past A Semi Infinite Flat Plate with Thermal Dispersion”, Int. J. of Non-Linear Science. 11, 301-311 (2011). |
| [10] | Mansour M. A. and Gorla R. S. R.: Mixed convection-radiation interaction in power- law fluids along a non-isothermal wedge embedded in a porous medium. Transport in Porous Media. 30, 113-124 (1998). |
| [11] | M. M. Alim, M.A. Alim and M.K. Chowdhury.: Effect of pressure stress work and viscous dissipation in natural convection flow along a vertical plate with heat conduction. J. Naval and Marine Eng. 3, 69-76 (2006). |
| [12] | Jha B.K. and Ajibade A.O.: Effect of viscous dissipation on natural convection flow between vertical plates with time period boundary conditions, Thermophys. Areo tech. 17, 1576-1587 (2011). |
| [13] | Nazma Parveen, Sujon Nath, Md. Abdul Alim.: Viscous dissipation Effect on Natural Convection Flow along a vertically wavy surface. 90, 294-300 (2014). |
| [14] | A. Shahzad, R Ali, MHD flow of a non-Newtonian Power law fluid over a vertical stretching sheet with the convective boundary condition, Walailak Journal of Science and Technology (WJST) 10 (1), 43-56 (2013). |
| [15] | A. Shahzad, R. Ali, Approximate analytic solution for magneto-hydrodynamic flow of a non-Newtonian fluid over a vertical stretching sheet. Can J Appl Sci 2, 202-215 (2012). |
| [16] | M. Khan, R. Ali, A. Shahzad MHD Falkner-Skan flow with mixed convection and convective boundary conditions. Walailak Journal of Science and Technology (WJST) 10 (5), 517-529 (2013). |
| [17] | J Ahmed, A Shahzad, A Begum, R Ali, N Siddiqui, Effects of inclined Lorentz forces on boundary layer flow of Sisko fluid over a radially stretching sheet with radiative heat transfer, Journal of the Brazilian Society of Mechanical Sciences and Engineering, 1-12 (2017). |
| [18] | A Shahzad, R Ali, M Hussain, M Kamran, Unsteady axisymmetric flow and heat transfer over time-dependent radially stretching sheet, Alexandria Engineering Journal 56, 35-41 (2017). |
| [19] | J Ahmed, T Mahmood, Z Iqbal, A Shahzad, R Ali: Axisymmetric flow and heat transfer over an unsteady stretching sheet in power law fluid, Journal of Molecular Liquids 221, 386-393 (2016). |
| [20] | K.C. Saha, M.A. Samad and M.R. Hossain: Effect of viscous dissipation on MHD Free Convection flow Heat and Mass Transfer of Non-Newtonian Fluids along a Continuously moving Stretching Sheet, Research J. of App. Sciences, Eng. And Tech., pp. 1058-1073 (2015). |
| [21] | Chen, C.H.: Effects of magnetic field and sunction/injection on the convective heat transfer on the non-Newtonian power law fluids past a power law stretched sheet with surface heat flux. Int.J. Therm. Sci 47, 954-961(2008). |




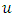 of
of 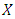 axis pertains along the surface and the
axis pertains along the surface and the 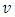 of
of 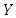 axis normal to the surface of the sheet. Two equal and opposite forces are performed to keep the origin fixed for
axis normal to the surface of the sheet. Two equal and opposite forces are performed to keep the origin fixed for 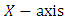 so that the sheet is stretched. The power law is used to describe fluid behavior, permit mathematical predictions, and correlate computerized experimental data in this case.
so that the sheet is stretched. The power law is used to describe fluid behavior, permit mathematical predictions, and correlate computerized experimental data in this case.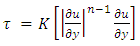
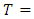
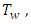 at
at 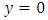 to
to 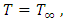 at
at 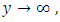 in the flow of outer region. This region is known as thermal boundary layer. Suppose, no change of temperature profiles of the surface
in the flow of outer region. This region is known as thermal boundary layer. Suppose, no change of temperature profiles of the surface 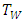 as well as the free stream temperature profile
as well as the free stream temperature profile 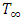 are taken respectively. For natural convection the flow is induced by a force known as buoyancy forces, which arise from density
are taken respectively. For natural convection the flow is induced by a force known as buoyancy forces, which arise from density 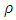 differences caused by the variation of temperature in the region. If we go through molecular level of the fluid, it shows us the changes of temperature profiles such as
differences caused by the variation of temperature in the region. If we go through molecular level of the fluid, it shows us the changes of temperature profiles such as 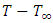 is arisen by the different values of temperature of the fluid particle. The relative change is calculated as
is arisen by the different values of temperature of the fluid particle. The relative change is calculated as 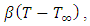 where
where 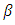 is designated as the volumetric coefficient of thermal expansion. Gravitational force is involved because of buoyancy force. In this case,
is designated as the volumetric coefficient of thermal expansion. Gravitational force is involved because of buoyancy force. In this case, 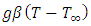 is the lift force per unit volume where gravitational acceleration
is the lift force per unit volume where gravitational acceleration 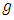 is working through vertical axis. Hence,
is working through vertical axis. Hence, 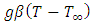 is active at
is active at 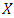 dirction.
dirction. 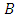 is used as applied magnetic field which is reliable on fluid’s characters. But it causes the growth of magnetic force
is used as applied magnetic field which is reliable on fluid’s characters. But it causes the growth of magnetic force 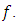
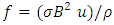 To describe this discrete mathematical problem let us formulate the governing equations as follows:
To describe this discrete mathematical problem let us formulate the governing equations as follows: 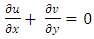
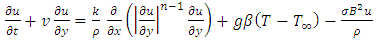
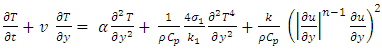
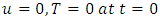 and Boundary conditions:
and Boundary conditions: 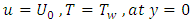 and
and 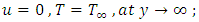 for
for 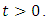

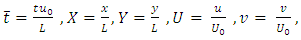
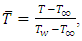 Where L is the characteristic length and
Where L is the characteristic length and 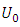 is an arbitrary reference velocity which is related to this problem. Since free stream conditions are quiescent in free convection, there is no logical external reference velocity
is an arbitrary reference velocity which is related to this problem. Since free stream conditions are quiescent in free convection, there is no logical external reference velocity 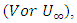 as in forced convection. The radiative heat flux
as in forced convection. The radiative heat flux 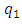 is described by the Rosseland approximation such that,
is described by the Rosseland approximation such that, 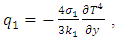 Note that Rosseland approximation is valid for optically thick fluids.
Note that Rosseland approximation is valid for optically thick fluids. 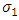 is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and 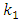 is the Rosseland mean absorption coefficient. It is surmised that the temperature difference within the flow is sufficiently small such that that
is the Rosseland mean absorption coefficient. It is surmised that the temperature difference within the flow is sufficiently small such that that 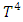 can be can be expressed in the Taylor series, where free stream temperature
can be can be expressed in the Taylor series, where free stream temperature 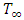 and neglecting the higher order terms from Taylor series expansion
and neglecting the higher order terms from Taylor series expansion 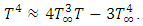 Therefore,
Therefore, 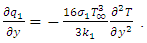 So, the dimensionless momentum equation and ultimate dimensionless energy equation are:
So, the dimensionless momentum equation and ultimate dimensionless energy equation are: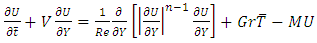
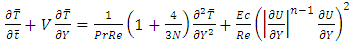
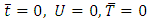 and Boundary condition at
and Boundary condition at 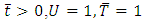 when
when 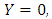
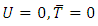 when
when 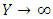 . (7) Where, the radiation number
. (7) Where, the radiation number 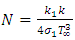 , Reynolds number
, Reynolds number 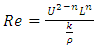 , Prandlt Number
, Prandlt Number 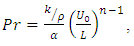 Eckert number
Eckert number 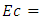
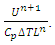 Here the modified version of dimensionless numbers are used. Note that, those numbers are valid for this fluid flow only. It may appear different in different flows.
Here the modified version of dimensionless numbers are used. Note that, those numbers are valid for this fluid flow only. It may appear different in different flows.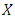 and
and 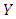 axes, where
axes, where 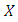 is chosen along the stretching surface and
is chosen along the stretching surface and 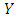 is normal to the plate.
is normal to the plate. 
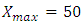 which indicates that x varies from 0 to 50 where
which indicates that x varies from 0 to 50 where 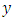 varies for 0 to
varies for 0 to 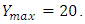 So the step size is calculated below.Here
So the step size is calculated below.Here 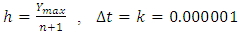 and for grid spacing
and for grid spacing 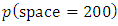 and
and 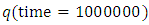 in the
in the 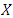 and
and 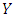 directions respectively.Two point forward difference formula for determining time derivatives, two point central difference method has chosen to approximate the space involving derivatives and three point central difference approximation to find double derivative. Now the equations (5) to (7) becomes:
directions respectively.Two point forward difference formula for determining time derivatives, two point central difference method has chosen to approximate the space involving derivatives and three point central difference approximation to find double derivative. Now the equations (5) to (7) becomes: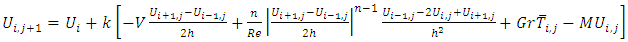
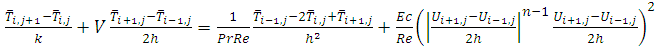
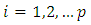 and
and 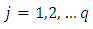 Initial condition at
Initial condition at 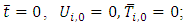 Boundary condition at
Boundary condition at 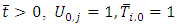
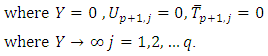
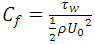 and the Nusselt number is,
and the Nusselt number is, 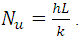 Using FDM the discretize equations are
Using FDM the discretize equations are 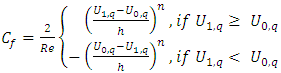 and
and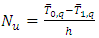
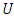 and temperature profile
and temperature profile 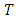 are obtained at all internal node points by successive application of the equations (7) to (9). The whole process will be done again and again and used time step will be sufficiently small. Effects of dimensionless numbers on velocity and temperature has been depicted through graphs. Using (10) skin friction coefficients and Nusselt numbers are obtained then solutions are shown in the table.From the Figure 5.1 the velocity profile decreases with the increase of magnetic parameter M in each type of fluid. It has been obtained that, introducing magnetic field in the flow causes higher restriction to the fluid. For Newtonian and pseudo plastic fluid the velocity profile reduces in same rate but in case of dilatant fluid rate of reduction is little bit slower. Thus, velocity profile decreases as
are obtained at all internal node points by successive application of the equations (7) to (9). The whole process will be done again and again and used time step will be sufficiently small. Effects of dimensionless numbers on velocity and temperature has been depicted through graphs. Using (10) skin friction coefficients and Nusselt numbers are obtained then solutions are shown in the table.From the Figure 5.1 the velocity profile decreases with the increase of magnetic parameter M in each type of fluid. It has been obtained that, introducing magnetic field in the flow causes higher restriction to the fluid. For Newtonian and pseudo plastic fluid the velocity profile reduces in same rate but in case of dilatant fluid rate of reduction is little bit slower. Thus, velocity profile decreases as 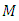 increases in all types of fluids which reduces faster for Newtonian fluid compared to non-Newtonian fluids. But in case of temperature profile there is no significant effect found.
increases in all types of fluids which reduces faster for Newtonian fluid compared to non-Newtonian fluids. But in case of temperature profile there is no significant effect found.

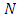 . Form above result, we observe that the small increment cause a lot to the thermal boundary layer. Temperature profile reduces to zero slowly. So from the above illustration it is evident that numerical outcomes support the physical experiment (Newton’s law of cooling). The rate of heat transfer is thus increased. So we can use the effect of radiation to control the velocity and temperature of boundary layer.
. Form above result, we observe that the small increment cause a lot to the thermal boundary layer. Temperature profile reduces to zero slowly. So from the above illustration it is evident that numerical outcomes support the physical experiment (Newton’s law of cooling). The rate of heat transfer is thus increased. So we can use the effect of radiation to control the velocity and temperature of boundary layer.
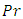 on velocity profile shows significant changes for the increase of its magnitude. From the figure it can be told the rate of reduction is little for three types of fluid for large Prandtl number but for small Prandtl number such as
on velocity profile shows significant changes for the increase of its magnitude. From the figure it can be told the rate of reduction is little for three types of fluid for large Prandtl number but for small Prandtl number such as 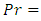
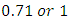 the reduction rate is larger. However for
the reduction rate is larger. However for 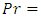
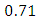 there is a sharp rise in the velocity boundary layers near stretching surface. Physically
there is a sharp rise in the velocity boundary layers near stretching surface. Physically 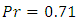 corresponds to air and
corresponds to air and 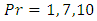 is for different values of water. For pseudo plastic fluid the velocity profile rise higher and slowly decreases to zero at the wall.
is for different values of water. For pseudo plastic fluid the velocity profile rise higher and slowly decreases to zero at the wall.
 steps. But when
steps. But when 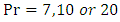 then profiles raises a little at the beginning and then slowly reduces to zero at the wall. The rate of reduction is almost same for these three types of fluid. Moreover, cross flows have been found for each case.
then profiles raises a little at the beginning and then slowly reduces to zero at the wall. The rate of reduction is almost same for these three types of fluid. Moreover, cross flows have been found for each case.


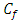 reduces with the increment of
reduces with the increment of 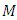 but
but 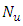 remain unchanged.
remain unchanged. 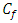 and
and 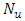 decreased significantly for the increase of
decreased significantly for the increase of 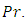 In this case cross flow has been found.
In this case cross flow has been found. 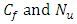 shows opposite scenario. Where skin friction increases slowly and Nusselt number decreases, although the effect is very small. Thermal radiation can be used to control the boundary layer. Skin friction coefficient
shows opposite scenario. Where skin friction increases slowly and Nusselt number decreases, although the effect is very small. Thermal radiation can be used to control the boundary layer. Skin friction coefficient 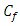 has decreased slowly but Nusselt number
has decreased slowly but Nusselt number 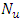 effect shows diversity for the increase of N in case of different power law index n.To show the validity of the model described above, skin friction coefficient as well as heat transfer rate have been calculated and compared to the Chen (2008) model for specific parameter.
effect shows diversity for the increase of N in case of different power law index n.To show the validity of the model described above, skin friction coefficient as well as heat transfer rate have been calculated and compared to the Chen (2008) model for specific parameter. 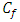 decreased but
decreased but 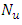 has increased with the growth of
has increased with the growth of 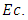
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
