-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2017; 7(2): 46-50
doi:10.5923/j.ajcam.20170702.03

Existence and Uniqueness of Nonlinear Implicit Fractional Differential Equation with Riemann-Liouville Derivative
1Department of Mathematics, North Maharashtra University, Jalgaon, India
2Department of Mathematics, R. C. Patel Arts, Commerce and Science College, Shirpur, India
Correspondence to: H. L. Tidke, Department of Mathematics, North Maharashtra University, Jalgaon, India.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We study an initial value problem for nonlinear implicit fractional differential equation with Riemann-Liouville fractional derivative. In the process, we obtain the existence and uniqueness of solutions of an implict fractional differential equation by Banach fixed point theorem. Further, we discuss the uniqueness of solutions via the application of Bihari and Medved inequalities.
Keywords: Riemann-Liouville fractional derivative, Fractional integral, Fixed point theorem, Implicit fractional differential equation, Bihari and Medved inequalities
Cite this paper: H. L. Tidke, R. P. Mahajan, Existence and Uniqueness of Nonlinear Implicit Fractional Differential Equation with Riemann-Liouville Derivative, American Journal of Computational and Applied Mathematics , Vol. 7 No. 2, 2017, pp. 46-50. doi: 10.5923/j.ajcam.20170702.03.
Article Outline
1. Introduction
- The study of fractional calculus that grows out of traditional concepts of the calculus derivative and integral operators. Several authors were introduced many different forms of noninteger differential operators and discussed varous results on existence, uniqueness; and qualitative and quantative properties of solutions for fractional differential equations, the reader referred to [7, 11, 12, 16, 23] and the monographs: Samko et al. (1993); Miller et al. (1993); Podlubny (1999); Hilfer (2000); Kilbas et al. (2006); Cresson (2007); Diethem K. (2010); Katugampola (2011) and Abbas S. et al. (2012).Podlubny I. [20], studied the existence and uniqueness of an initial value problem:
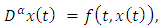 | (1.1) |
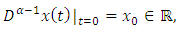 | (1.2) |
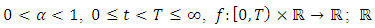 denotes the real space and
denotes the real space and 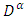 denotes Riemann-Liouville fractional derivative operator. Recently, Chinchane V. L. and Pachpatte D. B. [2] have discussed the uniqueness of solution of fractional differential equation with the Riemann-Liouville derivative. Existence and uniqueness of an implicit fractional differential equations via the Liouville-Caputo derivative have studied by authors in [17] using the fixed point concepts. Kucche et al. [10] investigated existence, uniqueness, continuous dependence and estimates of solutions for an implicit fractional differential equations.Motivated by the above mentioned works in this manuscript, we discuss the existence and uniqueness of the solution for the following implicit fractional differential equations with Riemann-Liouville derivative:
denotes Riemann-Liouville fractional derivative operator. Recently, Chinchane V. L. and Pachpatte D. B. [2] have discussed the uniqueness of solution of fractional differential equation with the Riemann-Liouville derivative. Existence and uniqueness of an implicit fractional differential equations via the Liouville-Caputo derivative have studied by authors in [17] using the fixed point concepts. Kucche et al. [10] investigated existence, uniqueness, continuous dependence and estimates of solutions for an implicit fractional differential equations.Motivated by the above mentioned works in this manuscript, we discuss the existence and uniqueness of the solution for the following implicit fractional differential equations with Riemann-Liouville derivative: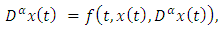 | (1.3) |
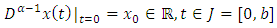 | (1.4) |
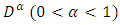 denotes Riemann-Liouville fractional derivative operator and
denotes Riemann-Liouville fractional derivative operator and 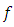 is real conitnuous valued function on
is real conitnuous valued function on 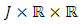 into
into 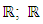 denotes the real space.Furthermore, our intention is to extend the results presented by Chinchane V. L. and Pachpatte D. B. to nonlinear implicit fractional differential equation. The paper is organized as follows. In Section 2, some definitions, lemmas and preliminary results are intoduced to be used in the sequel. Section 3 will involve the assumptions and main result of existence and uniqueness by fixed point theorerm. Finally Section 4 deal the results of uniqueness for the problem (1.3)-(1.4) via inequalities.
denotes the real space.Furthermore, our intention is to extend the results presented by Chinchane V. L. and Pachpatte D. B. to nonlinear implicit fractional differential equation. The paper is organized as follows. In Section 2, some definitions, lemmas and preliminary results are intoduced to be used in the sequel. Section 3 will involve the assumptions and main result of existence and uniqueness by fixed point theorerm. Finally Section 4 deal the results of uniqueness for the problem (1.3)-(1.4) via inequalities.2. Preliminaries
- Let us recall some definitions and concepts of the fractional calculus [9, 10, 15, 17, 20, 21] and state the few results which are used throuhout this paper. Definition 2.1. The fractional derivative of order
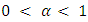 of a continuous function
of a continuous function 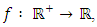 is given by
is given by 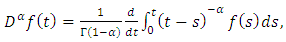 | (2.1) |
 Definition 2.2. The fractional primitive of order
Definition 2.2. The fractional primitive of order  of a function
of a function 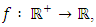 is given as follows
is given as follows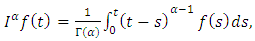 | (2.2) |
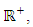 where
where 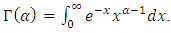 In [19], Medved introduced a special class of nonlinear functions and developed a method to estimate solution for nonlinear integral inequalities with singular kernel. The functions of such class are defined as follows:Definition 2.3. Let
In [19], Medved introduced a special class of nonlinear functions and developed a method to estimate solution for nonlinear integral inequalities with singular kernel. The functions of such class are defined as follows:Definition 2.3. Let 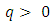 be a real number and
be a real number and 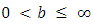 . The function w:
. The function w: 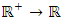 satisfies the following condition
satisfies the following condition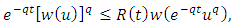 | (2.3) |
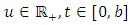 , where
, where 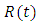 is a continuous, nonnegative function.Remark 2.1. If
is a continuous, nonnegative function.Remark 2.1. If 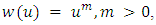 then
then 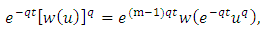 | (2.4) |
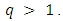 i.e the condition (2.3) is satisfies with
i.e the condition (2.3) is satisfies with 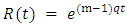 . For
. For 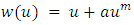 , where
, where 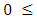
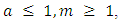 the function
the function 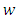 satisfies the condition (2.3) with
satisfies the condition (2.3) with 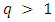 and
and 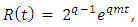 see [14].Lemma 2.1 [19] Let
see [14].Lemma 2.1 [19] Let 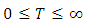 ,
,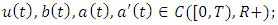
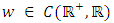 be nondecreasing function,
be nondecreasing function, 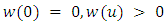 on
on 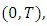 and
and 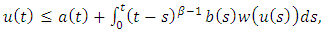 | (2.5) |
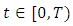 where
where 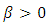 is constant. Then following hold:(i) Suppose
is constant. Then following hold:(i) Suppose 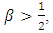 and if
and if 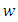 satisfies the condition (2.3) with
satisfies the condition (2.3) with 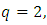 then
then 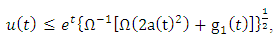 | (2.6) |
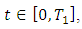 where
where 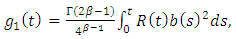 | (2.7) |
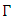 is gamma function,
is gamma function, 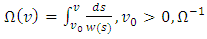 is the inverse of
is the inverse of 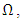 and
and 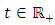 is such that
is such that 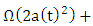
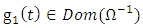 for all
for all 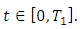 (ii) Let
(ii) Let 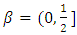 and
and 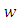 satisfies the condition (2.3) with
satisfies the condition (2.3) with 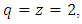 where
where 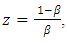 i. e.
i. e. 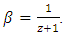 Let
Let 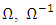 be as in part (i). Then
be as in part (i). Then 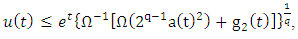 | (2.8) |
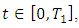 where
where 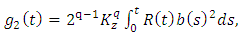 | (2.9) |
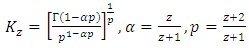 | (2.10) |
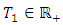 is such that
is such that 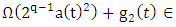
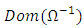 for all
for all 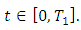 Lemma 2.2 [19] Let
Lemma 2.2 [19] Let 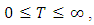
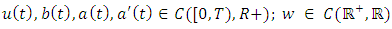 and
and 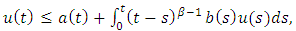 | (2.11) |
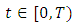 where
where 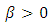 is constant. Then following hold:(i) Suppose
is constant. Then following hold:(i) Suppose 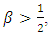 then
then 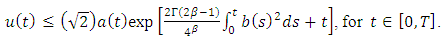 | (2.12) |
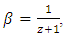 for some
for some 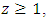 then
then 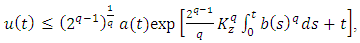 | (2.13) |
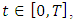 where
where 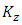 is defined as in (2.10),
is defined as in (2.10), 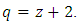 For detail proof of above two theorems see [16].Lemma 2.3 ([3, 18], p. 152) (Bihari inequality) Let
For detail proof of above two theorems see [16].Lemma 2.3 ([3, 18], p. 152) (Bihari inequality) Let 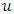 and
and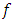 be nonnegative defined on
be nonnegative defined on 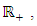 let
let 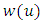 be continuous nondecreasing function defined on
be continuous nondecreasing function defined on 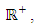 and
and 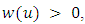 on
on 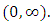 If
If 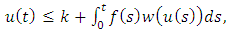 | (2.14) |
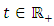 where
where 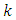 is nonnegative constant, for
is nonnegative constant, for 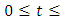
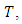
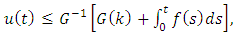 | (2.15) |
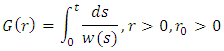 and
and 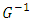 is the inverse fucntion of
is the inverse fucntion of 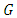 and
and 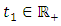 is chosen so that
is chosen so that 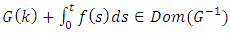 for all
for all 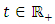 laying in the interval
laying in the interval 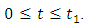 Lemma 2.4 Let
Lemma 2.4 Let 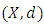 be a non-empty complete metric space with a contraction mapping
be a non-empty complete metric space with a contraction mapping 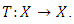 Then
Then 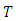 admits a unique fixed point
admits a unique fixed point 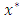 in
in 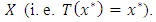
3. Existence and Uniqueness
- In this section, we prove existence and uniqueness result for the problem (1.3)-(1.4). We first note that if
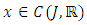 is an absolutely continuous function satisfying (1.3)-(1.4), then
is an absolutely continuous function satisfying (1.3)-(1.4), then 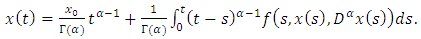 | (3.1) |
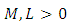 such that
such that 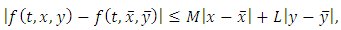 | (3.2) |
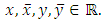
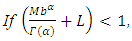 then the problem (1.3)-(1.4) has unique solution
then the problem (1.3)-(1.4) has unique solution 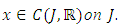 Proof. Consider a function
Proof. Consider a function 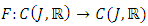 and defined by
and defined by 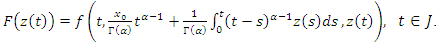 | (3.3) |
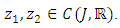 Then we have
Then we have 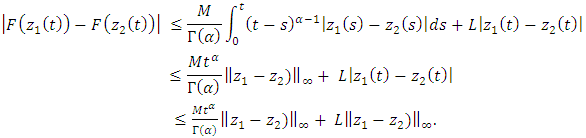 | (3.4) |
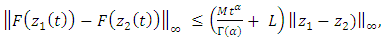 | (3.5) |
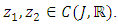 From the Banach fixed point theorem, Lemma 2.4, there exists a unique
From the Banach fixed point theorem, Lemma 2.4, there exists a unique 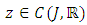 such that
such that 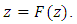 Therefore
Therefore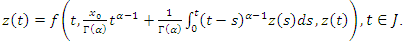 | (3.6) |
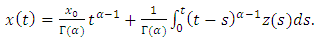 | (3.7) |
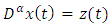 and therefore
and therefore 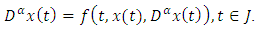 This shows that the function
This shows that the function 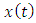 satisfies the problem (1.3)-(1.4) and uniqueness of the solution follows from the unique existence of
satisfies the problem (1.3)-(1.4) and uniqueness of the solution follows from the unique existence of 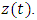 This completes the proof of the theorem.
This completes the proof of the theorem.4. Uniqueness via Inequalites
- In this section, we discuss the uniqueness of solution of the initial value problem (1.3)-(1.4).Theorem 4.1 If
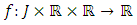 is continuous and satisfies condition
is continuous and satisfies condition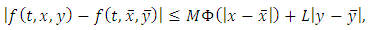 | (4.1) |
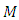 is positive constant,
is positive constant, 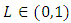 and
and 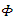 is a continuous nondecreasing function on
is a continuous nondecreasing function on 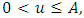 with
with 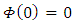 and
and 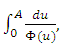 | (4.2) |
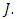 Proof. Let
Proof. Let 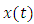 and
and 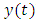 be two solutions of the problem (1.3)-(1.4). Then we have
be two solutions of the problem (1.3)-(1.4). Then we have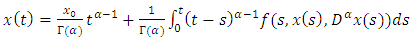 | (4.3) |
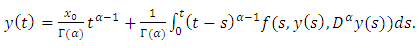 | (4.4) |
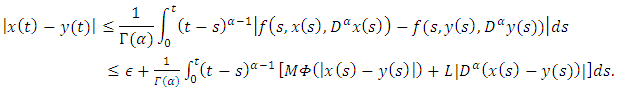 | (4.5) |
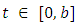 and any
and any 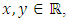
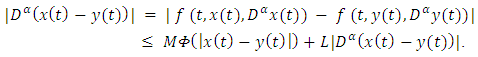 This implies
This implies 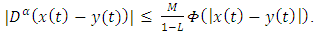 | (4.6) |
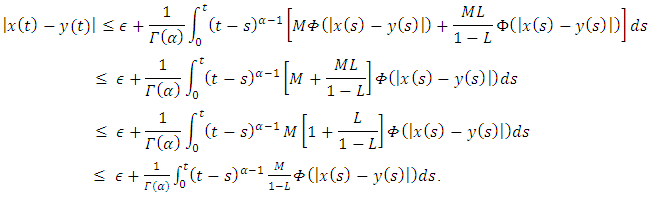 | (4.7) |
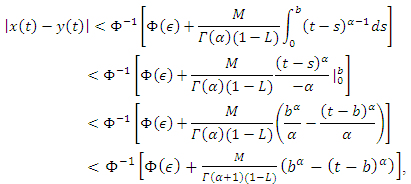 | (4.8) |
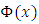 is primitive for
is primitive for 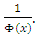 We shall prove that the right-hand side of (4.8) tends toward zero as
We shall prove that the right-hand side of (4.8) tends toward zero as 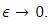 As
As 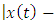
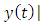 is independent of
is independent of 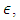 it follows that
it follows that 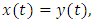 which we need. Let us remark that condition (4.2) implies
which we need. Let us remark that condition (4.2) implies 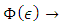
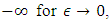 no matter how we choose the primitive of
no matter how we choose the primitive of 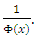 Thus
Thus 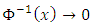 as
as 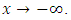 Consequently,
Consequently, 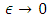 in the inequality (4.8), the right-hand side tends toward zero. This completes the proof of the theorem.Theorem 4.2 If the function
in the inequality (4.8), the right-hand side tends toward zero. This completes the proof of the theorem.Theorem 4.2 If the function 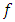 is continuous and satisfies the conditionz
is continuous and satisfies the conditionz | (4.9) |
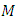 and
and 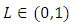 then the initial value problem (1.3)-(1.4) has unique solution in the interval
then the initial value problem (1.3)-(1.4) has unique solution in the interval 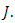 Proof. Let
Proof. Let 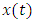 and
and 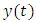 be two solutions of the problem (1.3)-(1.4). Then we have
be two solutions of the problem (1.3)-(1.4). Then we have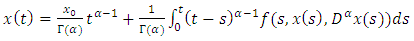 | (4.10) |
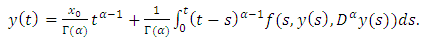 | (4.11) |
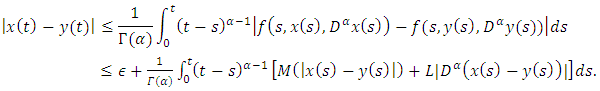 | (4.12) |
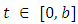 and any
and any 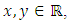
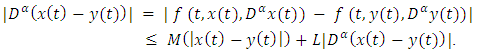 This implies
This implies 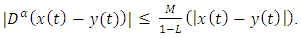 | (4.13) |
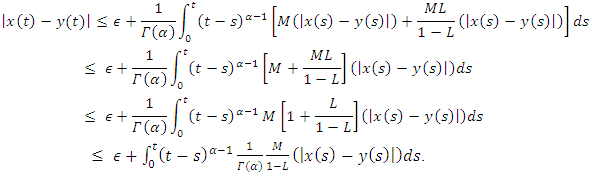 | (3.14) |
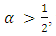 then applying Leema 2.2 (i) to (4.14), we have
then applying Leema 2.2 (i) to (4.14), we have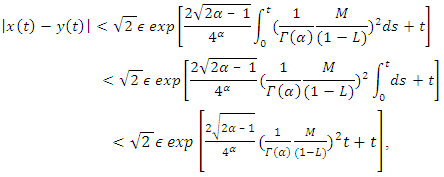 | (4.15) |
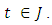 Since
Since 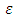 was arbitrary, as
was arbitrary, as 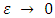 the inequality (4.13) implies that
the inequality (4.13) implies that 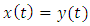 on
on 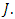 (b) Let
(b) Let 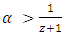 for some
for some 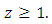 Then by Lemma 2.2 (ii) to (4.14), again we have,
Then by Lemma 2.2 (ii) to (4.14), again we have,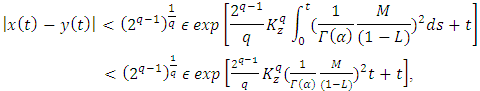 | (4.16) |
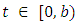 where
where 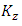 is defined by (2.10). Since
is defined by (2.10). Since 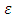 was arbitrary in (4.16), implies that
was arbitrary in (4.16), implies that 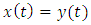 as
as 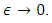 This completes the proof of the theorem.
This completes the proof of the theorem. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML