-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2017; 7(2): 33-36
doi:10.5923/j.ajcam.20170702.01

Optimal Designs Technique for Solving Unconstrained Optimization Problems with Univariate Quadratic Surfaces
Idorenyin A. Etukudo
Department of Mathematics & Statistics, Akwa Ibom State University, Mkpat Enin, Nigeria
Correspondence to: Idorenyin A. Etukudo, Department of Mathematics & Statistics, Akwa Ibom State University, Mkpat Enin, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The author presented a new approach for solving unconstrained optimization problems having univariate quadratic surfaces. An illustrative example using this technique shows that an optimizer could be reached in just one move which compares favorably with other known ones, say, Fibonacci Search technique.
Keywords: Fibonacci search technique, Unconstrained optimization, Response surface, Modified super convergent line series algorithm, Optimal designs of experiment
Cite this paper: Idorenyin A. Etukudo, Optimal Designs Technique for Solving Unconstrained Optimization Problems with Univariate Quadratic Surfaces, American Journal of Computational and Applied Mathematics , Vol. 7 No. 2, 2017, pp. 33-36. doi: 10.5923/j.ajcam.20170702.01.
Article Outline
1. Introduction
- In this paper, an alternative technique for solving unconstrained optimization problems with univariate quadratic surfaces is proposed. In real life, only very few problems exist where managers are concerned with taking decisions involving only one decision variable and without constraints. However, the justification for the study of such problems stem from the fact that it forms the basis of simple extensions and plays a key role to the development of a general multivariate algorithms as stated in [1] and [2].According to [3], there are many iterative techniques for solving first unconstrained nonlinear problems and these techniques usually require many iterations of very tedious computations. Fibonacci Search and Golden Section Search techniques are some of the direct search techniques in this group that are used for finding the optimum of an arbitrary unimodal unconstrained univariate response function. The idea here is to identify the interval of uncertainty containing this optimum and the computational efforts involved in the two techniques which seek to minimize the size of the interval are enormous. In the case of Fibonacci search technique, the search procedures depend on a numerical sequence known as Fibonacci numbers. This method successfully reduces the interval in which the optimum of an arbitrary nonlinear function must lie (See [1]). On the other hand, according to [4] and [5], Golden Section Search technique is another traditional method used for finding the optimum of an arbitrary unimodal univariate objective function. The superiority of this technique over Fibonacci is that there is need for apriori specification of the resolution factor as well as the number of iterations before the Fibonacci technique is used. These are not necessary in Golden section technique as apriori specification of these might not be possible in practice, [6]. However, [7] had shown that Fibonacci Search technique is the best traditional technique for finding the optimal point for a single valued function. See also [8].In order to circumvent these pitfalls, an alternative method for obtaining the required optimizer is of interest in this work which will later be generalized to accommodate response functions involving multi variables. The operation of the new algorithm makes use of the principles of optimal designs of experiment as can be seen in [9]. To design an experiment optimally, we select N support points within the experimental region such that optimal solution to the unconstrained optimization problems with univariate response surfaces could be realized. As by [10], a well-defined method to handle interactive effects in the case of quadratic surfaces has been provided. Since this new technique is a line search algorithm, it relies on a well-defined method of determining the direction of search as given by [11] which was a modification of [12]. See also [13]. This method seeks to determine the exact optimum of the unimodal unconstrained univariate response function rather than locating and reducing the interval where it lies which is the objective of the traditional methods. The algorithmic procedure which is given in the next section requires that the optimal support points that form the initial design matrix obtained from the entire experimental region be partitioned into r groups, r = 2, 3, … , n. However, [14] have shown that with r = 2, optimal solutions are obtained.
2. Optimal Designs Technique
- The sequential steps involved in this new method are given below.Initialization: Let the response function, f(x) be defined as f(x) = a0 + a1x + bx2 Select N support points such that 3r ≤ N ≤ 4r or 6 ≤ N ≤ 8where r = 2 is the number of partitioned groups and by choosing N arbitrarily, make an initial design matrix
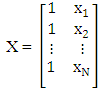 Step 1: Compute the optimal starting point,
Step 1: Compute the optimal starting point, 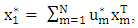 where
where 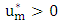 ,
, 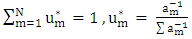 , m = 1, 2, …, N,
, m = 1, 2, …, N, 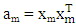 , m = 1, 2, …, N. Step 2: Partition X into r = 2 groups and obtain
, m = 1, 2, …, N. Step 2: Partition X into r = 2 groups and obtain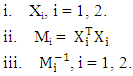 Step 3: Calculate the following:(i) The matrices of the interaction effect of the x variable for the groups as
Step 3: Calculate the following:(i) The matrices of the interaction effect of the x variable for the groups as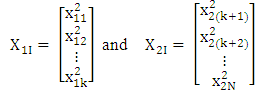 where
where 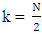 .(ii) Interaction vector of the response parameter, g = [b](iii) Interaction vectors,
.(ii) Interaction vector of the response parameter, g = [b](iii) Interaction vectors, 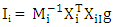 (iv) Matrices of mean square error,
(iv) Matrices of mean square error, 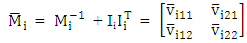 (v) Hessian matrices,
(v) Hessian matrices, 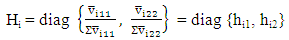 (vi) Normalized Hi as
(vi) Normalized Hi as 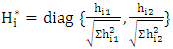 (vii) The average information matrix,
(vii) The average information matrix,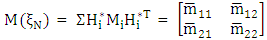 Step 4: Obtaini. The response vector,
Step 4: Obtaini. The response vector, 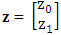 where
where 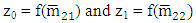 ii. The direction vector,
ii. The direction vector, 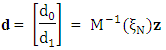 which gives
which gives 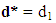 Step 5:Make a move to the point
Step 5:Make a move to the point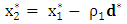 for a minimization problem or
for a minimization problem or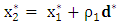 for a maximization problem where
for a maximization problem where 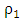 is the step length obtained from
is the step length obtained from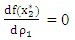 Step 6: Termination criteria. Is
Step 6: Termination criteria. Is 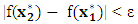 where ε = 0.0001?i. Yes. Stop and set
where ε = 0.0001?i. Yes. Stop and set 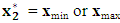 . as the case may be.ii. No. Replace
. as the case may be.ii. No. Replace 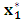 by
by 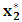 and return to step 5. If
and return to step 5. If 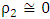 , then implement step 6(i).
, then implement step 6(i).3. Numerical Illustration
- In this section, we give a numerical illustration of the optimal designs technique for solving unconstrained optimization problems with univariate quadratic surfaces. The example below gives such an illustration.
3.1. Example
- min f(x) = x2SolutionInitialization: Given the response function, f(x) = x2 select N support points such that 3r ≤ N ≤ 4r or 6 ≤ N ≤ 8 where r = 2 is the number of partitioned groups and by choosing N arbitrarily, make an initial design matrix
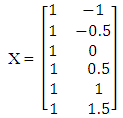 Step 1: Compute the optimal starting point,
Step 1: Compute the optimal starting point, 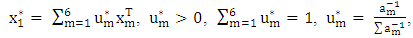
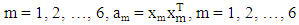
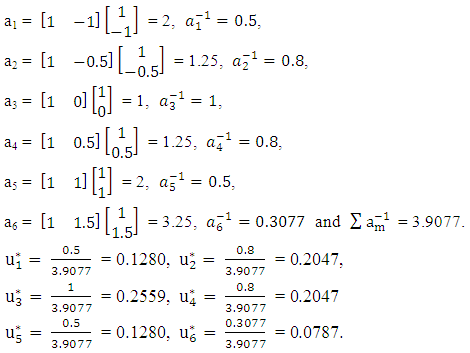 Hence, the optimal starting point is
Hence, the optimal starting point is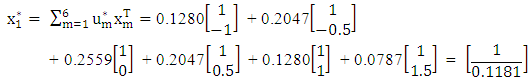 Step 2: By partitioning X into 2 groups, we have the design matrices,
Step 2: By partitioning X into 2 groups, we have the design matrices, 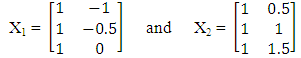 The information matrices are
The information matrices are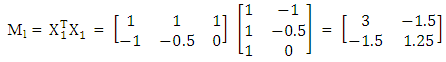 and
and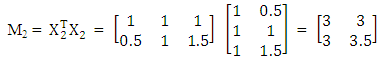 and their inverses are
and their inverses are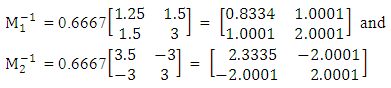 Step 3 Calculate the following:(i) The matrices of the interaction effect of the univariate for the groups as
Step 3 Calculate the following:(i) The matrices of the interaction effect of the univariate for the groups as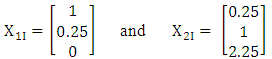 (ii) Interaction vector of the response parameter,g = [1](iii) Interaction vectors for the groups to be
(ii) Interaction vector of the response parameter,g = [1](iii) Interaction vectors for the groups to be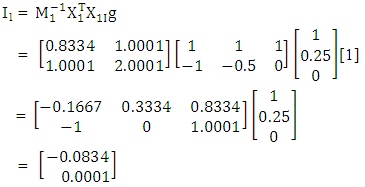
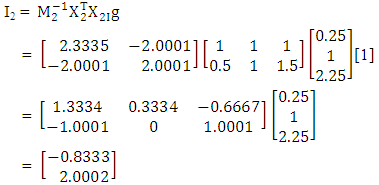 (iv) Matrices of mean square error for the groups are
(iv) Matrices of mean square error for the groups are 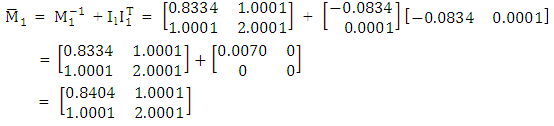
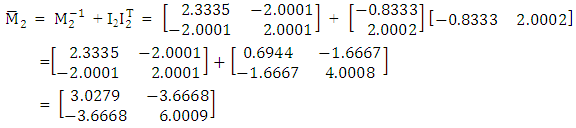 (v) Matrices of coefficient of convex combinations of the matrices of mean square error are
(v) Matrices of coefficient of convex combinations of the matrices of mean square error are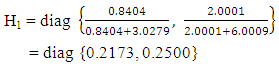 H2 = I – H1 = diag {0.7827, 0.7500}and by normalizing Hi such that
H2 = I – H1 = diag {0.7827, 0.7500}and by normalizing Hi such that 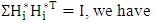
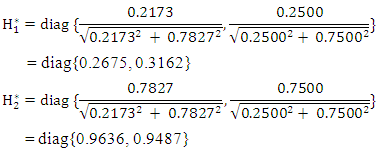 (vi) The average information matrix is
(vi) The average information matrix is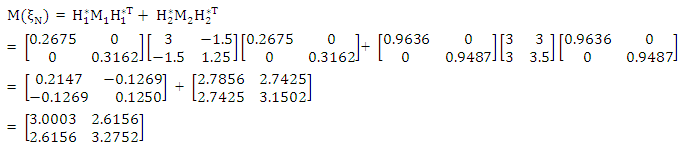 Step 4 Obtain the response vector
Step 4 Obtain the response vector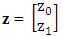 That is,z0 = f(2.6156) = 2.61562 = 6.8414z1 = f(3.2752) = 3.27522 = 10.7269and hence, the direction vector
That is,z0 = f(2.6156) = 2.61562 = 6.8414z1 = f(3.2752) = 3.27522 = 10.7269and hence, the direction vector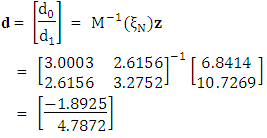 which gives d* = d1 = 4.7872Step 5 Make a move to the point
which gives d* = d1 = 4.7872Step 5 Make a move to the point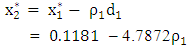 That is,
That is,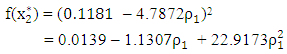 and by derivative with respect to
and by derivative with respect to 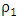 , we have
, we have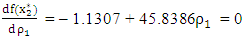 which gives the step length as
which gives the step length as 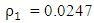 and
and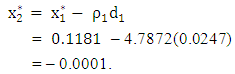
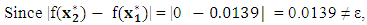 We make a second move to the point
We make a second move to the point 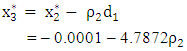 That is,
That is,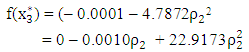 and by derivative with respect to
and by derivative with respect to 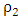 , we have
, we have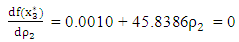 which gives the step length as
which gives the step length as 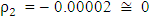 . This means that the optimal solution was obtained at the first move and and hence,
. This means that the optimal solution was obtained at the first move and and hence,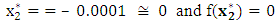 This result is more efficient than that obtained by Fibonacci search technique which gave xmin = (0.0472, - 0. 0184) and f(xmin) = (0.0022, 0.0003).
This result is more efficient than that obtained by Fibonacci search technique which gave xmin = (0.0472, - 0. 0184) and f(xmin) = (0.0022, 0.0003).4. Conclusions
- We have successfully achieved the primary objective of this work by presenting an efficient alternative technique for solving unconstrained optimization problems having univariate quadratic surfaces. This was done by using the principles of optimal designs of experiment to show that the optimum could be obtained in just one move. A numerical illustration by this method which gave
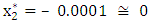 and
and 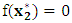 as the exact solution is more efficient than
as the exact solution is more efficient than 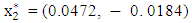 and
and 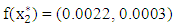 obtained from Fibonacci Search technique with several iterations.
obtained from Fibonacci Search technique with several iterations. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML