-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2017; 7(1): 11-24
doi:10.5923/j.ajcam.20170701.02

Information Measure Approach for Calculating Model Uncertainty of Physical Phenomena
Boris Menin
Mechanical & Refrigeration Consultant Expert, Beer-Sheba, Israel
Correspondence to: Boris Menin, Mechanical & Refrigeration Consultant Expert, Beer-Sheba, Israel.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, we aim to establish the specific foundations in modeling the physical phenomena. For this purpose, we discuss a representation of information theory for the optimal design of the model. We introduce a metric called comparative uncertainty by which a priori discrepancy between the chosen model and the observed material object is verified. Moreover, we show that the information quantity inherent in the model can be calculated and how it proscribes the required number of variables which should be taken into account. It is thus concluded that in most physically relevant cases (micro- and macro-physics), the comparative uncertainty can be realized by field tests or computer simulations within the prearranged variation of the main recorded variable. The fundamentally novel concept of the introduced uncertainty can be widely used and is universally valid. We introduce examples of the proposed approach as applied to Heisenberg's uncertainty relation, heat and mass transfer equations, and measurements of the fine structure constant.
Keywords: Information theory, Similarity theory, Mathematical modeling, Heisenberg uncertainty relation, Heat and mass transfer, Fine structure constant
Cite this paper: Boris Menin, Information Measure Approach for Calculating Model Uncertainty of Physical Phenomena, American Journal of Computational and Applied Mathematics , Vol. 7 No. 1, 2017, pp. 11-24. doi: 10.5923/j.ajcam.20170701.02.
Article Outline
1. Introduction
- This paper represents our attempt towards establishing the universal metric of the uncertainty value of micro- and macro-physics mathematical models by the application of information theory. The very act of a measurement process already implies an existence of the formulated physical-mathematical model describing the phenomenon under investigation. Measurement theory focuses on the measurement process of experimentally determining the value of a quantity with the help of special technical means called measuring instruments [1]. It covers only aspects of the measuring procedure and data analysis of the observed or researched variable after formulating the mathematical model. So, the issue of uncertainty that exists before the beginning of the experiment or computer simulation and arising as a result of the limited number of variables recorded in the mathematical model is generally ignored in measurement theory. In the scientific community the prevailing view is the more precise the instrument used for the model development, the more accurate the results, and the measurement uncertainty is also lower. Basically, in our everyday world it is possible to reduce the uncertainty in the determination of the studied process to a minimum. This, in turn, causes a widely held opinion that the usage of supercomputers, a huge number of simulations and large scale mathematical modeling can allow us to reach a high degree of accuracy of the model describing the observed material system [2-4]. For example, a standard input file of Energyplus as published by the US Department of Energy as a beta-testing of a whole-building simulation engine to describe a building has about 3,000 inputs. Its preliminary calculated uncertainty of, for example, room temperature, is very hard to estimate, because it strongly depends on the accuracy of the modeling inputs. Without measured data to compare and calibrate, energy simulation results can easily be 50–200% of the actual building energy use. For this reason it is not possible to validate a model and its results, but only to increase the level of confidence that is placed in them [5].In contrast to the above-mentioned opinion, human intuition and experience suggests the simple, at first glance, truth. For a small number of variables, the researcher gets a very rough picture of the process being studied. In turn, the huge number of accounted variables can allow deep and thorough understanding of the structure of the phenomenon. However, with this apparent attractiveness, each variable brings its own uncertainty into the integrated (theoretical or experimental) uncertainty of the model or experiment. In addition, the complexity and cost of computer simulations and field tests increases enormously. Therefore, some optimal or rational number of variables that is specific to each of the studied processes must be considered in order to evaluate the physical-mathematical model. This work seeks to develop a fundamentally novel method to characterize the model firstborn uncertainty (model discrepancy [6]) connected only with the finite number of recorded variables. Of course, in addition to this uncertainty, the overall measurement inaccuracy includes the posterior uncertainties related to the internal structure of the model and its subsequent computerization: inaccurate input data, inaccurate physical assumptions, the limited accuracy of the solution of integral-differential equations, etc. Detailed definitions of many different sources of these uncertainties are outlined in the literature [1, 6-8]. The introduced novel analysis is intended to help physicists and designers to determine the most simple and reliable way to select a model with the optimal number of recorded variables calculated according to the minimum achievable value of the model uncertainty.The present approach begins with the analysis of several publications related to usage of the concepts of "information quantity" and “entropy” for real applications in physics and engineering (Chapter 2), followed by the formulation of a system of dimensional variables, from which a modeler chooses variables in order to describe the researched process. Such a system must meet a certain set of axioms that form an Abelian group. This in turn allows the author to employ the approach for the calculation of the total number of dimensionless criteria in the existing International System of Units introduced in section 3.1. Mathematically, the exact expression for the calculation of the model’s uncertainty with a limited number of variables obtained by counting the quantity of information contained in the model is introduced in section 3.2. Application of the method to three problems widely different in their physical nature is presented in Chapter 4. A discussion regarding limits of the approach results and its advantages are formulated in Chapter 5. Conclusions are discussed in Chapter 6.
2. Preliminaries
- Modeling is an information process in which information about the state and behavior of the observed object is obtained by the developed model. This information is the main subject of interest of modeling theory. During the modeling process, the information increases, while the information entropy decreases due to increased knowledge about the object [9]. The extent of knowledge A of the observed object may be expressed in the form
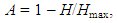 | (1) |
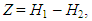 | (2) |
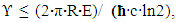 | (3) |
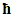 is the reduced Planck constant, and c is the speed of light. The results are purely theoretical in nature, although it is possible, judging by the numerous references to this article, that one may find applications of the proposed formula in medicine or biology. A study of quantum gates has been developed [13]. The author considered these gates as physical devices which are characterized by the existence of random uncertainty. Reliability of quantum gates was investigated from the perspective of information complexity. In turn, the complexity of the gate’s operation was determined by the difference between the entropies of the variables characterizing the initial and final states. The study has stated that the gate operation may be associated with unlimited entropy, implying the impossibility of realization of the quantum gates function under certain conditions. The relevance of this study comes from its conceptual approach of use of variables, as a specific metric for calculation of information quantity changing between input and output of the apparatus model.The information theory-based principles have been investigated in relation to uncertainty of mathematical models of water-based systems [14]. In this research, the mismatch between physically-based models and observations has been minimized by the use of intelligent data-driven models and methods of information theory. The real successes were achieved in developing forecast models for the Rhine and Meuse rivers in the Netherlands. In addition to the possibility of forecasting the uncertainties and accuracy of model predictions, the application of information theory principles indicates that, alongside appropriate analysis techniques, patterns in model uncertainties can be used as indicators to make further improvements to physically-based computational models. At the same time, there have been no attempts to apply these methodologies to results to other physical or engineering tasks. The design information entropy was introduced as a state that reflects both complexity and refinement [15]. The author argued that it can be useful as some measure of design efficacy and design quality. The method has been applied to the conceptual design of an unmanned aircraft, going through concept generation, concept selection, and parameter optimization. For the purposes of this study it is important to note that introducing the design information entropy as a state can be used as a quantitative description for various aspects in the design process, both with regards to structural information of architecture and connectivity, as well as for parameter values, both discrete and continuous.In [16] there has been conducted a systematic review of major physical applications of information theory to physical systems, its methods in various subfields of physics, and examples of how specific disciplines adapt this tool. In the context of the proposed approach for practical purposes in experimental and theoretical physics and engineering, the physics of computation, acoustics, climate physics, and chemistry have been mentioned. However, no surveys, reviews, research studies were found with respect to apply information theory for calculating an uncertainty of models of the phenomenon or technological process. The approach that uses the tools of estimation theory to fuse together information from multi-fidelity analysis, resulting in a Bayesian-based approach to mitigating risk in complex design has been proposed [6]. Maximum entropy characterizations of model discrepancies have been used to represent epistemic uncertainties due to modeling limitations and model assumptions. The revolutionary methodology has been applied to multidisciplinary design optimization and demonstrated on a wing-sizing problem for a high altitude, long endurance aircraft. Uncertainties have been examined that have been explicitly maintained and propagated through the design and synthesis process, resulting in quantified uncertainties on the output estimates of quantities of interest. However, the proposed approach focuses on the optimization of the predefined and computer-ready simulation model.For these reasons there are only a handful of different methods and techniques used to identify matching of physical-mathematical models and studied physical phenomena or technological processes by the uncertainty formulated with usage of the concepts of "information quantity" and “entropy”. All the above-mentioned methodologies are focused on identifying a posterior uncertainty caused by the ineradicable gap between model and a physical system. At the same time, according to our data, in the modern literature there does not exist any physical or mathematical relationship which could formulate the interaction between the level of detailed descriptions of the material object (the number of recorded variables) and the lowest achievable total experimental uncertainty of the main parameter.Thus, it is advisable to choose the appropriate/acceptable level of detail of the object (a finite number of registered variables) and formulate the requirements for the accuracy of input data and the uncertainty of specific target function (similarity criteria), which describes the "livelihood" and characterizes the behavior of the observed object.
is the reduced Planck constant, and c is the speed of light. The results are purely theoretical in nature, although it is possible, judging by the numerous references to this article, that one may find applications of the proposed formula in medicine or biology. A study of quantum gates has been developed [13]. The author considered these gates as physical devices which are characterized by the existence of random uncertainty. Reliability of quantum gates was investigated from the perspective of information complexity. In turn, the complexity of the gate’s operation was determined by the difference between the entropies of the variables characterizing the initial and final states. The study has stated that the gate operation may be associated with unlimited entropy, implying the impossibility of realization of the quantum gates function under certain conditions. The relevance of this study comes from its conceptual approach of use of variables, as a specific metric for calculation of information quantity changing between input and output of the apparatus model.The information theory-based principles have been investigated in relation to uncertainty of mathematical models of water-based systems [14]. In this research, the mismatch between physically-based models and observations has been minimized by the use of intelligent data-driven models and methods of information theory. The real successes were achieved in developing forecast models for the Rhine and Meuse rivers in the Netherlands. In addition to the possibility of forecasting the uncertainties and accuracy of model predictions, the application of information theory principles indicates that, alongside appropriate analysis techniques, patterns in model uncertainties can be used as indicators to make further improvements to physically-based computational models. At the same time, there have been no attempts to apply these methodologies to results to other physical or engineering tasks. The design information entropy was introduced as a state that reflects both complexity and refinement [15]. The author argued that it can be useful as some measure of design efficacy and design quality. The method has been applied to the conceptual design of an unmanned aircraft, going through concept generation, concept selection, and parameter optimization. For the purposes of this study it is important to note that introducing the design information entropy as a state can be used as a quantitative description for various aspects in the design process, both with regards to structural information of architecture and connectivity, as well as for parameter values, both discrete and continuous.In [16] there has been conducted a systematic review of major physical applications of information theory to physical systems, its methods in various subfields of physics, and examples of how specific disciplines adapt this tool. In the context of the proposed approach for practical purposes in experimental and theoretical physics and engineering, the physics of computation, acoustics, climate physics, and chemistry have been mentioned. However, no surveys, reviews, research studies were found with respect to apply information theory for calculating an uncertainty of models of the phenomenon or technological process. The approach that uses the tools of estimation theory to fuse together information from multi-fidelity analysis, resulting in a Bayesian-based approach to mitigating risk in complex design has been proposed [6]. Maximum entropy characterizations of model discrepancies have been used to represent epistemic uncertainties due to modeling limitations and model assumptions. The revolutionary methodology has been applied to multidisciplinary design optimization and demonstrated on a wing-sizing problem for a high altitude, long endurance aircraft. Uncertainties have been examined that have been explicitly maintained and propagated through the design and synthesis process, resulting in quantified uncertainties on the output estimates of quantities of interest. However, the proposed approach focuses on the optimization of the predefined and computer-ready simulation model.For these reasons there are only a handful of different methods and techniques used to identify matching of physical-mathematical models and studied physical phenomena or technological processes by the uncertainty formulated with usage of the concepts of "information quantity" and “entropy”. All the above-mentioned methodologies are focused on identifying a posterior uncertainty caused by the ineradicable gap between model and a physical system. At the same time, according to our data, in the modern literature there does not exist any physical or mathematical relationship which could formulate the interaction between the level of detailed descriptions of the material object (the number of recorded variables) and the lowest achievable total experimental uncertainty of the main parameter.Thus, it is advisable to choose the appropriate/acceptable level of detail of the object (a finite number of registered variables) and formulate the requirements for the accuracy of input data and the uncertainty of specific target function (similarity criteria), which describes the "livelihood" and characterizes the behavior of the observed object. 3. Formulation of Applied Tools
3.1. System of Primary Variables
- The harmonic building of modern science is based on a simple consensus that any physical laws of micro- and macro-physics are described by quite certain dimensional variables. These variables are selected within a pre-agreed system of primary variables (SPV) such as SI (international system of units) or CGS (centimeter–gram–second system of units). The SPV is a set of dimensional variables (DL), which are primary and can generate secondary variables, which are necessary and sufficient to describe the known laws of nature, as in the quantitative physical content [17]. This means that any scientific knowledge and all, without exception, formulated physical laws are discovered due to information contained in SPV. This is a unique channel (generalizing carrier of information) through which information is transmitted to the observer or the observer extracts information about the object from SPV. SPV includes a finite number of physical DL variables which have the potential to characterize the world’s physical properties and, in particular, observed phenomenon qualitatively and quantitatively. So, an observation of a material object and its modeling are framed by SPV. We model only what we can imagine or observe, and the mere presence of a selected SPV, such as the lens, sets a specific limit on measurement of the observed object.In turn, SPV includes the primary and secondary variables used for descriptions of different classes of phenomena (COP). In other words, the additional limits of the description of the studied material object are caused due to the choice of COP and the number of secondary parameters taken into account in the mathematical model [18]. For example, in mechanics SI uses the basis {L– length, M– mass, Т– time}, i.e. COPSI ≡ LMT. Basic accounts of electromagnetism here add the magnitude of electric current I. Thermodynamics requires the inclusion of thermodynamic temperature Θ. For photometry it needs to add J– force of light. The final primary variable of SI is a quantity of substance F.If SPV and COP are not given, then the definition of "information about researched object" loses its force. Without SPV, the modeling of phenomenon is impossible. You can never get something out of nothing, not even by watching [19]. It is possible to interpret SPV as a basis of all accessible knowledge that humans are able to have about their environment at the present time. In turn, establishment of a specific SPV (e.g. SI units) means that we are talking about trying to restrict the set of possible variables by a smaller number of basic variables and the corresponding units. Then all other required variables can be found or determined based on these primary variables, which must meet certain criteria [17] that are introduced below. Let the different types of variables be denoted by A, B, C. Then the following relations must be realized:a. From A and B a new type of value is obtained as: C = A · B (multiplicative relationship); b. There are unnamed numbers, denoted by (I) = (A°), which when multiplied by A do not change the dimensions of this type of variables. A · (I) = A (single item); c. There must exist a variable which corresponds to the inverse of the variable 𝐴, which we denote
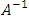 , such that
, such that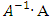 ; d. The relation between the different types of variables obeys the laws of associativity and commutativity: Associativity:
; d. The relation between the different types of variables obeys the laws of associativity and commutativity: Associativity: 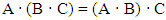 , Commutativity: A · B = (B · A); e. For all A ≠ (1) and m ∈ N; m ≠ 0, the expression
, Commutativity: A · B = (B · A); e. For all A ≠ (1) and m ∈ N; m ≠ 0, the expression 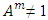 is the case; f. The complete set consisting of an infinite number of types of variable has a finite generating system. This means that there are a finite number of elements C1, C2… CH, through which any type of variable q can be represented as
is the case; f. The complete set consisting of an infinite number of types of variable has a finite generating system. This means that there are a finite number of elements C1, C2… CH, through which any type of variable q can be represented as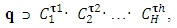 | (4) |
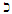 – means "corresponds to dimension";
– means "corresponds to dimension"; 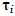 – integer coefficients,
– integer coefficients, 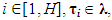 where λ is the set of integers.The uniqueness of such a representation is not expected in advance. Axioms “a-f” form a complete system of axioms of an Abelian group. By taking into account the basic equations of the theory of electricity, magnetism, gravity and thermodynamics, they remain unchanged.Now we use the theorem that holds for an Abelian group: among H elements of the generating system C1, C2… CH there is a subset
where λ is the set of integers.The uniqueness of such a representation is not expected in advance. Axioms “a-f” form a complete system of axioms of an Abelian group. By taking into account the basic equations of the theory of electricity, magnetism, gravity and thermodynamics, they remain unchanged.Now we use the theorem that holds for an Abelian group: among H elements of the generating system C1, C2… CH there is a subset 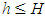 of elements B1, B2… Bh, with the property that each element can be uniquely represented in the form
of elements B1, B2… Bh, with the property that each element can be uniquely represented in the form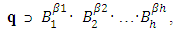 | (5) |
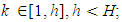 elements
elements 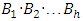 are called the basis of the group, and
are called the basis of the group, and 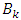 are the basic types of variables.
are the basic types of variables. 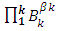 is the product of the dimensions of the main types of variables
is the product of the dimensions of the main types of variables 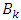 .For the above-stated conditions the following statement holds: the group, which satisfies axioms a-f, has, at least, one basis
.For the above-stated conditions the following statement holds: the group, which satisfies axioms a-f, has, at least, one basis 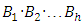 . In the case h > 2, there are infinitely many valid bases. How to determine the number of elements of a basis? In order to answer this question, let’s apply the approach introduced for the SI units. In this case, you need to pay attention to the following irrefutable situation. We should be aware that the condition (4) is a very strong constraint. It is well known that not every physical system can be represented as an Abelian group. Presentation of experimental results as a formula, in which the main parameter is represented in the form of the correlation function of the one-parameter selected functions, has many limitations [18]. However, in this study, the condition (4) can be successfully applied to the dummy system, in terms of lack in nature, which is SI. In this system, the secondary variables are always presented as the product of the primary variables in different powers.The entire information above can be represented as follows: 1. There are ξ = 7 primary variables: L – length, M – mass, Т – time, I– electric current, Θ– thermodynamic temperature, J– force of light, F– the number of substances [20];2. The dimension of any secondary variable q can only be expressed as a unique combination of dimensions of the main primary variables to different powers [17]:
. In the case h > 2, there are infinitely many valid bases. How to determine the number of elements of a basis? In order to answer this question, let’s apply the approach introduced for the SI units. In this case, you need to pay attention to the following irrefutable situation. We should be aware that the condition (4) is a very strong constraint. It is well known that not every physical system can be represented as an Abelian group. Presentation of experimental results as a formula, in which the main parameter is represented in the form of the correlation function of the one-parameter selected functions, has many limitations [18]. However, in this study, the condition (4) can be successfully applied to the dummy system, in terms of lack in nature, which is SI. In this system, the secondary variables are always presented as the product of the primary variables in different powers.The entire information above can be represented as follows: 1. There are ξ = 7 primary variables: L – length, M – mass, Т – time, I– electric current, Θ– thermodynamic temperature, J– force of light, F– the number of substances [20];2. The dimension of any secondary variable q can only be expressed as a unique combination of dimensions of the main primary variables to different powers [17]: 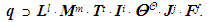 | (6) |
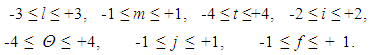 | (7) |
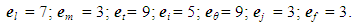 | (8) |
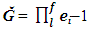
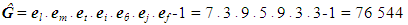 | (9) |
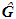 includes both required, and inverse variables (for example, L¹ – length, L-1 – running length). The object can be judged knowing only one of its symmetrical parts, while others structurally duplicating this part may be regarded as information empty. Therefore, the number of options of dimensions may be reduced by ω = 2 times. This means that the total number of dimension options of physical variables without inverse variables equals
includes both required, and inverse variables (for example, L¹ – length, L-1 – running length). The object can be judged knowing only one of its symmetrical parts, while others structurally duplicating this part may be regarded as information empty. Therefore, the number of options of dimensions may be reduced by ω = 2 times. This means that the total number of dimension options of physical variables without inverse variables equals 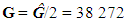 . 7. For further discussion we use the methods of the theory of similarity, which is expedient for several reasons. In the study of the phenomena occurring in the world around us, it is advisable to consider not individual variables but their combination or complexes which have a definite physical meaning. Methods of the theory of similarity based on the analysis of integral-differential equations and boundary conditions, allow for the identification of these complexes. In addition, the transition from DL physical quantities to dimensionless (DS) variables reduces the number of variables taken into account. The predetermined value of DS complex can be obtained by various combinations of DL variables included in the complex. This means that when considering the challenges of new variables we take into account not an isolated case, but a series of different events, united by some common properties. It is important to note that the universality of similarity transformations is defined by the invariant relationships that characterize the structure of all the laws of nature, including for the laws of relativistic nuclear physics. Moreover, dimensional analysis from the point of view of the mathematical apparatus has a group structure, and conversion factors (the similarity complexes) are invariants of the groups. The concept of the group is a mathematical representation of the concept of symmetry, which is one of the most fundamental concepts of modern physics [21].According to π-theorem [22], the number
. 7. For further discussion we use the methods of the theory of similarity, which is expedient for several reasons. In the study of the phenomena occurring in the world around us, it is advisable to consider not individual variables but their combination or complexes which have a definite physical meaning. Methods of the theory of similarity based on the analysis of integral-differential equations and boundary conditions, allow for the identification of these complexes. In addition, the transition from DL physical quantities to dimensionless (DS) variables reduces the number of variables taken into account. The predetermined value of DS complex can be obtained by various combinations of DL variables included in the complex. This means that when considering the challenges of new variables we take into account not an isolated case, but a series of different events, united by some common properties. It is important to note that the universality of similarity transformations is defined by the invariant relationships that characterize the structure of all the laws of nature, including for the laws of relativistic nuclear physics. Moreover, dimensional analysis from the point of view of the mathematical apparatus has a group structure, and conversion factors (the similarity complexes) are invariants of the groups. The concept of the group is a mathematical representation of the concept of symmetry, which is one of the most fundamental concepts of modern physics [21].According to π-theorem [22], the number  of possible DS complexes (criteria) with ξ = 7 main DL variables for SI will be
of possible DS complexes (criteria) with ξ = 7 main DL variables for SI will be | (10) |
 can only increase with the deepening of knowledge about the material world. It should be mentioned that the set of DS variables
can only increase with the deepening of knowledge about the material world. It should be mentioned that the set of DS variables 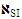 is a fictitious system, since it does not exist in physical reality. However, this observation is true for proper SI too. At the same time, the object which exists in actuality may be expressed by this set. The relationships (6)–(9) are obtained on the basis of the principles of the theory of groups as set forth in [17]. The present results provide a possible use of information theory to different physical and engineering areas with a view to formulating precise mathematical relationships to assess the minimum comparative uncertainty (see section 3.2) of the model that describes the studied physical phenomenon or process.
is a fictitious system, since it does not exist in physical reality. However, this observation is true for proper SI too. At the same time, the object which exists in actuality may be expressed by this set. The relationships (6)–(9) are obtained on the basis of the principles of the theory of groups as set forth in [17]. The present results provide a possible use of information theory to different physical and engineering areas with a view to formulating precise mathematical relationships to assess the minimum comparative uncertainty (see section 3.2) of the model that describes the studied physical phenomenon or process.3.2. Information Quantity Inherent to Model
- The validity of a mathematical model structure is confirmed, to a researcher, by the small differences between theoretical calculations and the experimental data. In doing so a question is overlooked: to what extent does the chosen model correctly describe the relevant natural phenomenon or process.In [23] it has been shown that by setting a priori the total value of uncertainties of an experiment and the formulated model, one can determine the necessary number of measurements of the chosen variable and the validity of the selected model. The specified approach at the decision of inverse mathematical tasks is based on the legitimacy of a condition [24]:
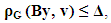 | (11) |
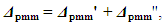 | (12) |
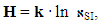 | (13) |
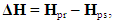 | (14) |
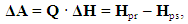 | (15) |
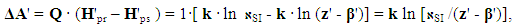 | (16) |
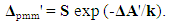 | (17) |
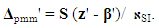 | (18) |
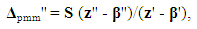 | (19) |
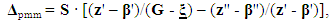 | (20) |
4. Applications of א -Hypothesis
4.1. Heisenberg’s Uncertainty Relation
- The numerical value of אSI can be calculated by the use of a heuristic approach with a relative uncertainty of 410-6, as
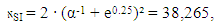 | (21) |
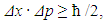 | (22) |
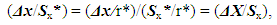 | (23) |
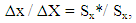 | (24) |
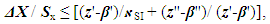 | (25) |
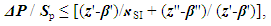 | (26) |
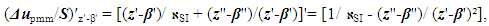 | (27) |
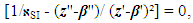 | (28) |
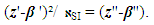 | (29) |
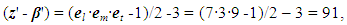 | (30) |
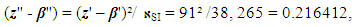 | (31) |
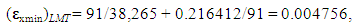 | (32) |
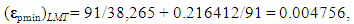 | (33) |
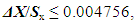 | (34) |
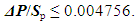 | (35) |
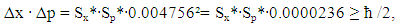 | (36) |
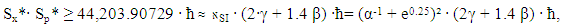 | (37) |
4.2. Heat and Mass-Transfer
- The process of heat transfer by freezing a thin layer of paste material posted onto a moving cooled cylinder wall has been investigated [33]. According to analysis of the recorded variables dimensions, the model is classified by COPSI ≡ LMTΘ. Let’s calculate z'-β'. According to (8)
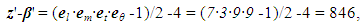 | (38) |
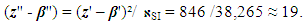 | (39) |
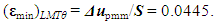 | (40) |
 was selected, where
was selected, where 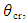
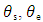 are the DL temperatures of the freezing point of a material, outer surface of a material layer and evaporation point of the refrigerant, respectively.
are the DL temperatures of the freezing point of a material, outer surface of a material layer and evaporation point of the refrigerant, respectively. 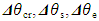 are the DL uncertainties of measurement of these temperatures. Their declared values were:
are the DL uncertainties of measurement of these temperatures. Their declared values were: 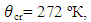
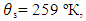
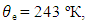
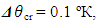
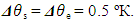 The declared achieved discrepancy between the experimental and computational data in the range of admissible values of the similarity criteria and dimensionless conversion factors did not exceed 8%.Taken into account was the fact that the direct measurement uncertainties are much smaller than the measured values, accounting for a few percent or less of them. The uncertainty can be considered formally as small increments of a measured variable. In practice, finite differences are used, rather than the differentials. So, in order to find the value of an absolute DS uncertainty
The declared achieved discrepancy between the experimental and computational data in the range of admissible values of the similarity criteria and dimensionless conversion factors did not exceed 8%.Taken into account was the fact that the direct measurement uncertainties are much smaller than the measured values, accounting for a few percent or less of them. The uncertainty can be considered formally as small increments of a measured variable. In practice, finite differences are used, rather than the differentials. So, in order to find the value of an absolute DS uncertainty 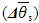 , the mathematical apparatus of differential calculus was applied [34]:
, the mathematical apparatus of differential calculus was applied [34]: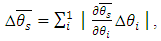 | (41) |
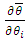 denotes the partial derivatives of the function
denotes the partial derivatives of the function 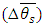 with respect to one of the several variables
with respect to one of the several variables 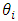 that affect
that affect 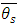 ; and
; and 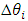 denotes the uncertainty of the variable
denotes the uncertainty of the variable 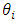 .For the present example, according to equation (40), one can find an absolute total DS uncertainty of the indirect measurement
.For the present example, according to equation (40), one can find an absolute total DS uncertainty of the indirect measurement 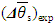 , reached in the experiment:
, reached in the experiment: 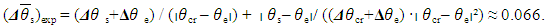 | (42) |
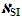 (9), z'-β' (38), and (z''-β'') (39), one obtains a DS uncertainty value
(9), z'-β' (38), and (z''-β'') (39), one obtains a DS uncertainty value 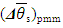 of the chosen model:
of the chosen model: 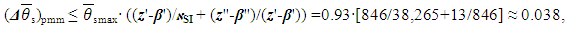 | (43) |
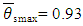 is the DS given range of changes of the DS final temperature allowed by the chosen model [33]. From (42) and (43) we get
is the DS given range of changes of the DS final temperature allowed by the chosen model [33]. From (42) and (43) we get 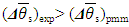 , i.e., an actual uncertainty in the experiment is 1.7 times (0.066/0.038) larger than the possible minimum. It means, at the recorded number of DS criteria the existing accuracy of the DL variable’s measurement is insufficient. In addition, the number of the chosen DS variables z*-β* = 13 is less than the recommended ≈ 19 (39) that corresponds to the lowest comparative uncertainty at COPSI ≡ LMTΘ. That is why, for further experimental work it is required to use devices of a higher class of accuracy sufficient to confirm/clarify a new model designed with many DS variables.In this example we introduce a full explanation of the required steps for analyzing experimental data and compare it with results obtained from a field test or computer simulation of model.
, i.e., an actual uncertainty in the experiment is 1.7 times (0.066/0.038) larger than the possible minimum. It means, at the recorded number of DS criteria the existing accuracy of the DL variable’s measurement is insufficient. In addition, the number of the chosen DS variables z*-β* = 13 is less than the recommended ≈ 19 (39) that corresponds to the lowest comparative uncertainty at COPSI ≡ LMTΘ. That is why, for further experimental work it is required to use devices of a higher class of accuracy sufficient to confirm/clarify a new model designed with many DS variables.In this example we introduce a full explanation of the required steps for analyzing experimental data and compare it with results obtained from a field test or computer simulation of model. 4.3. The Fine Structure Constant
4.3.1. First Example
- In [31] the authors have reported a new experimental scheme which combines atom interferometry with Bloch oscillations leading to a new determination of the fine structure constant (FSC)
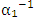 = 137.03599945(62) with a relative uncertainty r₁ of
= 137.03599945(62) with a relative uncertainty r₁ of 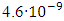 . In this case the absolute uncertainty was
. In this case the absolute uncertainty was 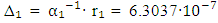 . The declared range S₁ of
. The declared range S₁ of 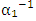 variations was
variations was 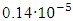 . Research is organized into the frame of COPSI ≡ LMТ. One can calculate the achieved comparative uncertainty as
. Research is organized into the frame of COPSI ≡ LMТ. One can calculate the achieved comparative uncertainty as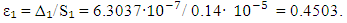 | (44) |
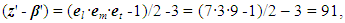 | (45) |
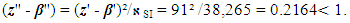 | (46) |
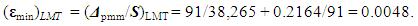 | (47) |
4.3.2. Second Example
- A recoil-velocity measurement of Rubidium has been conducted and a new determination of the FSC as
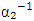 = 137.035999037(91) with a relative uncertainty of
= 137.035999037(91) with a relative uncertainty of 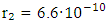 [35]. In this case the absolute uncertainty was
[35]. In this case the absolute uncertainty was 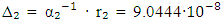 . The description of the experimental unit and methods corresponded to COPSI ≡ LMТ. According to equation (47), the lowest comparative uncertainty is equal to 0.0048. The range of variation S₂ of
. The description of the experimental unit and methods corresponded to COPSI ≡ LMТ. According to equation (47), the lowest comparative uncertainty is equal to 0.0048. The range of variation S₂ of 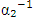 is
is 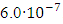 . In this case, the comparative uncertainty of the experimental method is
. In this case, the comparative uncertainty of the experimental method is 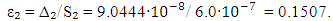 | (48) |
4.3.3. Third Example
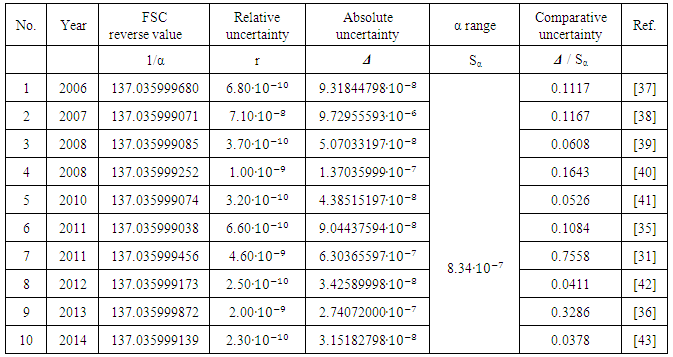
- Analysis of the FSC measurements made during 2006-2014. None of the current experimental measurements which calculate the FSC have declared an uncertainty interval in which the true value can be placed. Therefore, in order to apply the stated approach, as an estimated e error interval of FSC, we choose the difference of its value reached by the experimental results of two projects: (α') -1 = 137.035999872 [36] and (α'') -1 = 137.035999038 [35]. In this case the possible observed range S* of (α) -1 variation is equal to
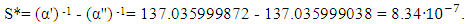 | (49) |
|
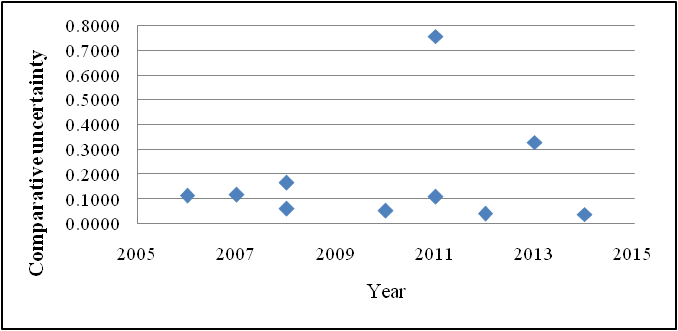 | Figure 1. A graph summarizing the partial history of the fine structure constant measurement displaying the decrease of the comparative uncertainty |
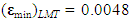 (47),
(47), 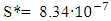 (49). Then the lowest possible absolute uncertainty for COPSI ≡LMТ is equal to
(49). Then the lowest possible absolute uncertainty for COPSI ≡LMТ is equal to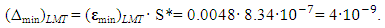 | (50) |
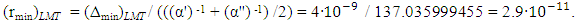 | (51) |
5. Discussion
- Despite the apparent attractiveness and versatility of the suggested approach, there are certain limitations, restrictions and occasions where its applicability is limited. They include the following:- The information-based approach requires the probable appearance of variables chosen by a conscious observer. It ignores factors such as developer knowledge, intuition, experience and environmental properties;- The approach requires the knowledge or declaration of the uncertainty interval of the main observed or researched variable. In reality, the value of this parameter is not declared in any serious experimental research in physics and engineering. Sometimes the uncertainty interval, for example, of Planck's constant, the speed of light and other fundamental physical constants, is mentioned in the review articles only in order to confirm the convergence of the experimental data to a certain value or reducing the spread of the results;- The method does not give any recommendations on the selection of specific physical variables, but only places a limit on their number.Nevertheless, the approach yields the universal metric by which the model discrepancy can be calculated. A more effective solution to finding the minimum uncertainty can be reached using the principles of information and similarity theories. Qualitative and quantitative conclusions drawn from the obtained relations are consistent with practice. They are as follows: Based on the information and similarity theories, a theoretical lowest value of the mathematical model uncertainty of the phenomenon or technological process can be derived. A numerical evaluation of this relation requires the knowledge of the error interval of the main researched variable and the required number of variables taken into account. In order to estimate the discrepancy between the chosen model measurement and the observed material object, a universal metric called comparative uncertainty has been developed further. Our analytical result for ε = Δpmm/S is a surprisingly simple relation.The author has carried out a theoretical evaluation of Heisenberg's uncertainty relation based on a mathematical formulation of the comparative uncertainty. This is the first time that this has been examined. When analyzing the modified Heisenberg uncertainty relation, the error interval of the particle location and the error interval of the particle momentum cannot be known with absolute precision simultaneously. This is an objective fact and is independent of the presence of the conscious observer conducting measurements. The more precisely the location of the particle is specified, the more uncertain a measurement of the momentum will be, and vice versa.Many attempts have been made to optimize a mathematical model of technological process or equipment which could bypass this. At that time, information and similarity theories were available for this purpose only. Satisfactory solutions could be achieved by applying the א-hypothesis and by taking the optimum number of variables into account. In addressing applications such as heat and mass transfer, full explanations of the required steps for analyzing experimental data and comparison with results obtained by a field test or computer simulation are introduced. From the present investigation one can conclude that the fundamentally novel analysis determines the most simple and reliable way to select a model with the optimal number of selected variables. This will greatly diminish the duration of the studies as well as the design stage, thereby reducing the cost of the project.The proposed methodology is an initial attempt to use a comparative uncertainty instead of relative uncertainty in order to compare the measurements results of the FSC and to verify its true value. A direct way to obtain reliable results has always been open, namely to assume that the FSC value lies within a chosen interval. However, this idea cannot be proved because of the difficulty of specifying the possible limit of the relative uncertainty. Of course, the choice of a value of the variation of (α) -1, S*, is controversial because of its apparent subjectivity. With these methods, our capacity to predict the FSC value by usage of the comparative uncertainty allows for an improvement of our fundamental comprehension of complex phenomenon, as well as allowing us to apply this understanding to the solution of specific problems. It may be the case that such findings will induce a negative reaction on the part of scientific community and some readers who consider the above examples as a game of numbers. In his defense, the author notes that eminent scientists such as Arnold Sommerfeld, Wolfgang Pauli and others scientists have followed a similar approach in order to approximate values for the FSC. The calculated results are routine calculations from formulas known in the scientific literature. At the same time, an additional perspective of the existing problem will, most likely, help us to understand the existing situation and identify concrete ways for its solution. Reducing the value of the comparative uncertainty of the FSC to the lowest achievable value of 0.0048 for the chosen COPSI ≡LMТ will serve as a convincing argument for professionals involved in the perfecting of SI.
6. Conclusions
- The measurement theory and its concepts remain a precise science today, in the twenty-first century, and will continue to be the case forever (a paraphrase of Prof. Okun [46]). The use of the א-hypothesis only limits the domain of applicability of measurement theory for uncertainties that are much larger than the uncertainty of the physical-mathematical model due to its finiteness.א-hypothesis might be applicable to experimental verification. In general, it is available when the researcher has all the information about the uncertainty interval of the main variable.The quantification of the model uncertainty via the information quantity value embedded in the physical-mathematical model opens up the possibility of linking the experimental and theoretical investigations by adopting the proposed approach for investigations into various physical phenomena or technological processes.The comparative uncertainty concept for calculating the optimal number of recorded variables and derived effects which are amenable to rigorous experimental verification have been introduced.One of the main results in the present paper is the proof of a necessary and sufficient condition for the correct choice of the number of variables recorded in a mathematical model describing physically observed phenomena and measurement processes.The author has proposed that the estimate of the a priori achievable uncertainty of a mathematical model due to a model’s finiteness (limited number of chosen variables), can be a peculiar metric for the assessing the accuracy of experimental measurements and computer simulation data.The author also hopes this paper stimulates readers to participate in the development of this approach in different fields of physics and engineering.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML