1. Introduction

The Klein-Gordon equation is a relativistic version of the Schrödinger equation describing free particles, which was proposed by Oskar Klein and Walter Gordon in 1926. It has many applications in Physics and Engineering such as quantum field theory, relativistic physics, dispersive wave-phenomena, plasma physics and nonlinear optics.

Various methods are developed to get approximate and numerical solutions of linear Klein-Gordon (LKG) and nonlinear Klein-Gordon (NLKG) equations as given below:

Deeba and Khuri [1]; El-Sayed [2]; Kaya and El-Sayed [3]; Wazwaz [4] used Adomian decomposition method (ADM) developed by Adomian in [5] for solving LKG and NLKG equations. Elcin Yusufoglu [6]; Batiha [7] used variational iteration method developed by J. H. He [8] to obtain an approximate solution of the NLKG equation. Yasir Khan [9] modified Laplace decomposition method proposed by Khuri in [10] to solve Klein-Gordon equations. Rabie [11] used Laplace decomposition method, Adomian decomposition method and modified Laplace decomposition method to solve NLKG equations and shown these three methods yield exactly the same result.

Y. Keskin and his associates [12] applied reduced differential transform method to calculate approximate analytical solution of the Klein-Gordon equations. Odibat and Momani [13] developed an algorithm of the Homotopy perturbation method to find the approximate solutions of the NLKG equations. D. Kumar and his associates in [14] developed an algorithm based on Homotopy analysis transform method to solve LKG and NLKG equations with initial conditions.

Dehghan and Shokri [15] applied radial basis functions to solve NLKG equations. Dehghan and Ghesmati in [16] applied the dual reciprocity boundary integral equation technique to obtain approximate analytical solution of the NLKG equations. H. M. Baskonus and H. Bulut [17] used the generalised Kudryashov method to obtain some new analytical solutions of the (1+1)-dimensional nonlinear dispersive modified Benjamin-Bona-Mahony equation and the (2+1)-dimensional cubic Klein-Gordon equation. Daftardar-Gejji and Jafari in [18] have introduced a new iterative method and used it to solve nonlinear functional equations.

The purpose of this paper is to apply double Laplace transform and iterative method developed in [18] to find the exact solution of nonlinear Klein-Gordon equation subject to initial and boundary conditions.

2. A Brief Introduction of Double Laplace Transforms

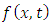Let be a function of two variables x and t defined in the positive quadrant of the xt-plane. The double Laplace transform of the function 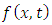as given by Ian N. Sneddon [19] is defined by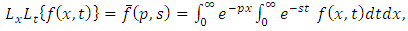

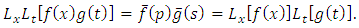
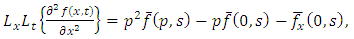
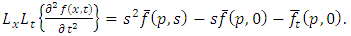
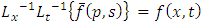(2.1)

whenever that integral exist. Here p and s are complex numbers.

From this definition we deduce

(2.2)

Further the double Laplace transform of second order partial derivatives as in [20, 21] are given by

(2.3)

(2.4)

The inverse double Laplace transform is defined as in [20, 21] by the complex double integral formula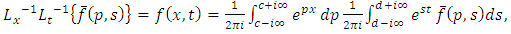

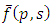(2.5)

where must be an analytic function for all p and s in the region defined by the inequalities 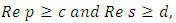where c and d are real constants to be chosen suitably.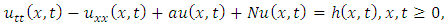

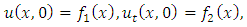
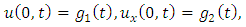
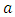3. Double Laplace Transform Coupled with Iterative Method

Consider the second order nonlinear Klein-Gordon equation

(3.1)

with initial conditions

(3.2)

and boundary conditions

(3.3)

where is a real number, 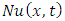is a non-linear term and 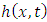is the source function.

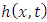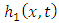We decompose the source function into and 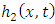. The part 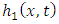with the linear terms in (3.1) always leads to the simple algebraic expression while applying the inverse double Laplace transform. The portion 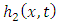is combined with the nonlinear term to avoid noise terms in the iteration process. In Section 4, while considering illustrative examples we see how to determine 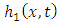and .

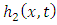Applying the double Laplace transform on both sides of (3.1), we get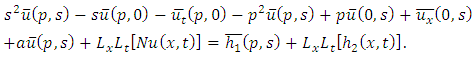

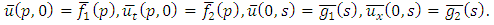
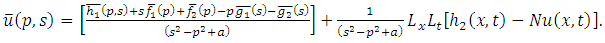
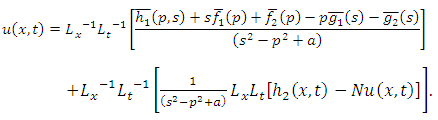
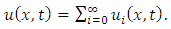
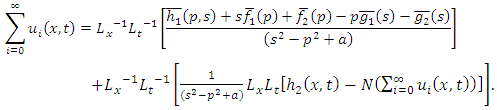
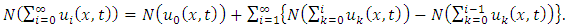
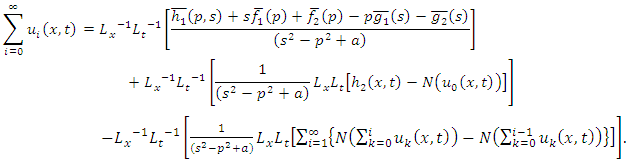
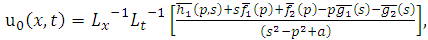
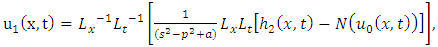
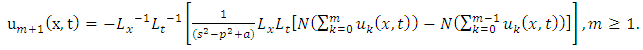
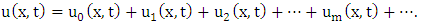
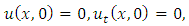
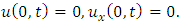
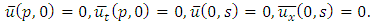
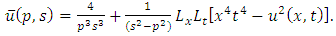
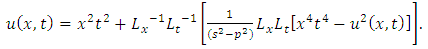
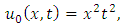
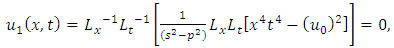
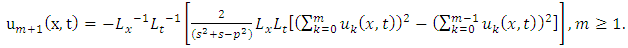
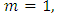
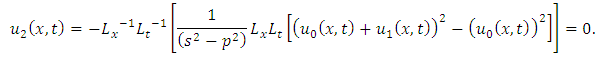(3.4)

Further, applying single Laplace transform to initial (3.2) and boundary conditions (3.3), we get

(3.5)

By substituting (3.5) in (3.4) and simplifying, we obtain

(3.6)

Applying inverse double Laplace transform to (3.6), we obtain

(3.7)

Now we apply the Iterative method as in [22],

(3.8)

Substitute (3.8) in (3.7), we get

(3.9)

The nonlinear term N is decomposed as

(3.10)

Substitute (3.10) in (3.9), we get

(3.11)

Then we define the recurrence relations as

(3.12)

(3.13)

(3.14)

Therefore, the solution of (3.1) in series form is given by

(3.15)

4. Illustrative Examples

In this section, we illustrate above method by giving some examples.

Example 4.1: Consider the following nonlinear Klein-Gordon equation similar to [23]

(4.1)

with initial conditions

(4.2)

and boundary conditions

(4.3)

Applying the double Laplace transform on both sides of (4.1), we get

(4.4)

Further, applying single Laplace transform to initial (4.2) and boundary conditions (4.3), we get

(4.5)

By substituting (4.5) in (4.4) and simplifying, we obtain

(4.6)

Applying inverse double Laplace transform to (4.6), we get

(4.7)

Now, applying the Iterative method.

Substituting (3.8) into (4.7) and applying (3.12), (3.13), (3.14), we obtain the components of the solution as follows:

(4.8)

(4.9)

(4.10)

From (4.8), (4.9) and (4.10) it is clear that for

Similarly, we have 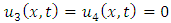and so on.

Therefore,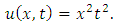

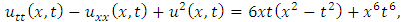
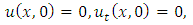
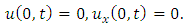
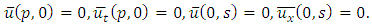
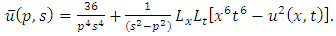
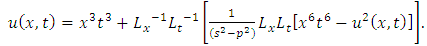
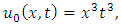
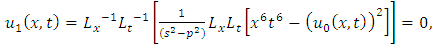
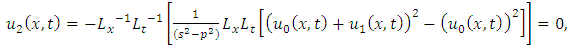
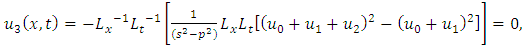
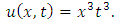
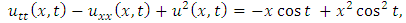
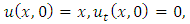
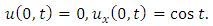
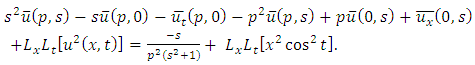
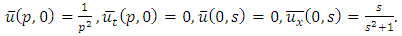
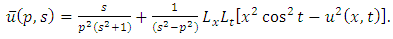
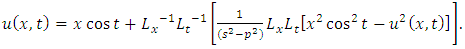
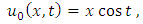
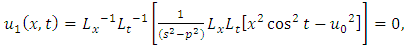
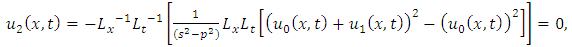
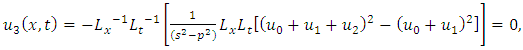
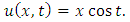
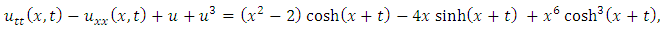
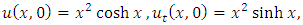
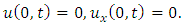
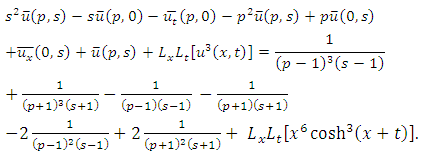
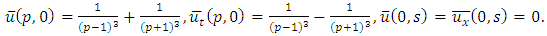
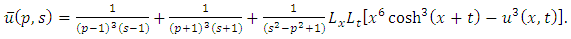
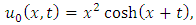
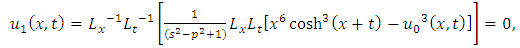
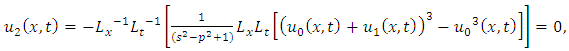
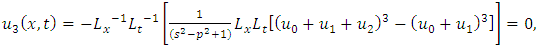
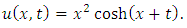
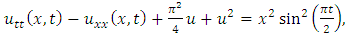
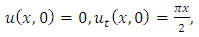
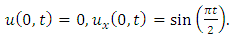
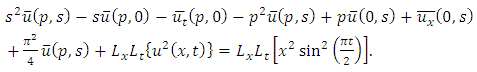
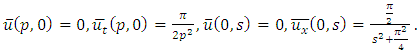
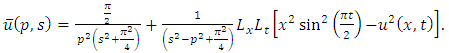
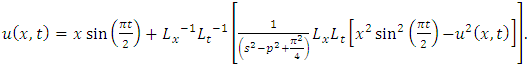
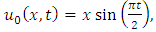
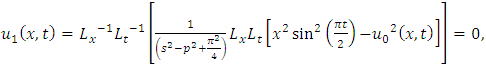
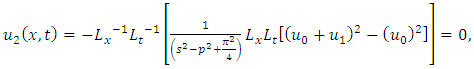
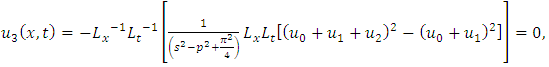
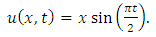
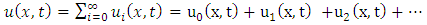(4.11)

This is the required exact solution of equation (4.1).

Example 4.2: Consider the following nonlinear Klein-Gordon equation similar to [24]

(4.12)

with initial conditions

(4.13)

and boundary conditions

(4.14)

Applying the double Laplace transform on both sides of (4.12), we get

(4.15)

Further, applying single Laplace transform to initial (4.13) and boundary conditions (4.14), we get

(4.16)

By substituting (4.16) in (4.15) and simplifying, we obtain

(4.17)

Applying inverse double Laplace transform to (4.17), we get

(4.18)

Now, applying the Iterative method.

Substituting (3.8) into (4.18) and applying (3.12), (3.13), (3.14), we obtain the components of the solution as follows:

(4.19)

(4.20)

(4.21)

(4.22)

and so on.

Therefore, we obtain the solution of (4.12) as follows:

(4.23)

Example 4.3: Consider the following nonlinear Klein-Gordon equation similar to [12]

(4.24)

with initial conditions

(4.25)

and boundary conditions

(4.26)

Applying the double Laplace transform on both sides of (4.24), we get

(4.27)

Further, applying single Laplace transform to initial (4.25) and boundary conditions (4.26), we get

(4.28)

By substituting (4.28) in (4.27) and simplifying, we obtain

(4.29)

Applying inverse double Laplace transform to (4.29), we get

(4.30)

Now, applying the Iterative method.

Substituting (3.8) into (4.30) and applying (3.12), (3.13), (3.14), we obtain the components of the solution as follows:

(4.31)

(4.32)

(4.33)

(4.34)

and so on.

Therefore, we obtain the solution of (4.24) as follows:

(4.35)

Example 4.4: Consider the following nonlinear Klein-Gordon equation

(4.36)

with initial conditions

(4.37)

and boundary conditions

(4.38)

Applying the double Laplace transform on both sides of (4.36), we get

(4.39)

Further, applying single Laplace transform to initial (4.37) and boundary conditions (4.38), we get

(4.40)

By substituting (4.40) in (4.39) and simplifying, we obtain

(4.41)

Applying inverse double Laplace transform to (4.41), we get

(4.42)

Now, applying the Iterative method.

Substituting (3.8) into (4.42) and applying (3.12), (3.13), (3.14), we obtain the components of the solution as follows:

(4.43)

(4.44)

(4.45)

(4.46)

and so on.

Therefore,

(4.47)

This is the required exact solution of equation (4.36).

Example 4.5: Consider the nonlinear Klein-Gordon equation similar to [25]

(4.48)

with initial conditions

(4.49)

and boundary conditions

(4.50)

Applying the double Laplace transform on both sides of (4.48), we get

(4.51)

Further, applying single Laplace transform to initial (4.49) and boundary conditions (4.50), we get

(4.52)

By substituting (4.52) in (4.51) and simplifying, we obtain

(4.53)

Applying inverse double Laplace transform to (4.53), we get

(4.54)

Now, applying the Iterative method.

Substituting (3.8) into (4.54) and applying (3.12), (3.13), (3.14), we obtain the components of the solution as follows:

(4.55)

(4.56)

(4.57)

(4.58)

and so on.

Therefore, we obtain the solution of (4.48) as follows:

(4.59)

5. Conclusions

From examples 4.1 to 4.5, we conclude that DLT combined with iterative method is adaptable to a wide range of nonlinear Klein-Gordon equations. In the solutions of most of the problems considered in [7, 11, 14, 23, 24] noise terms appear. By this method all nontrivial examples solved using earlier methods become trivial in the sense that the decomposition consists only of one term i.e. .

ACKNOWLEDGMENTS

The authors would like to express their sincere thanks to the referees for their valuable suggestions.