-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(5): 187-193
doi:10.5923/j.ajcam.20160605.03

Comparison of the COG Defuzzification Technique and Its Variations to the GPA Index
Michael Gr. Voskoglou
Department of Mathematical Sciences, School of Technological Applications, Graduate Technological Educational Institute (T. E. I.) of Western Greece, Patras, Greece
Correspondence to: Michael Gr. Voskoglou, Department of Mathematical Sciences, School of Technological Applications, Graduate Technological Educational Institute (T. E. I.) of Western Greece, Patras, Greece.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The Center of Gravity (COG) method is one of the most popular defuzzification techniques of fuzzy mathematics. In earlier works the COG technique was properly adapted to be used as an assessment model (RFAM) and several variations of it (GRFAM, TFAM and TpFAM) were also constructed for the same purpose. In this paper the outcomes of all these models are compared to the corresponding outcomes of a traditional assessment method of the bi-valued logic, the Grade Point Average (GPA) Index. Examples are also presented illustrating our results.
Keywords: Grade Point Average (GPA) Index,Center of Gravity (COG) Defuzzification Technique. Rectangular Fuzzy Assessment Model (RFAM), Generalized RFAM (GRFAM), Triangular (TFAM) and Trapezoidal (TpFAM) Fuzzy Assessment Models
Cite this paper: Michael Gr. Voskoglou, Comparison of the COG Defuzzification Technique and Its Variations to the GPA Index, American Journal of Computational and Applied Mathematics , Vol. 6 No. 5, 2016, pp. 187-193. doi: 10.5923/j.ajcam.20160605.03.
Article Outline
1. Introduction
- Fuzzy Logic (FL), due to its nature of characterizing the ambiguous situations of our day to day life by multiple values, offers rich resources for the assessment of such kind of situations. A characteristic example is the process of learning a subject matter, where the new knowledge is frequently connected to a degree of vagueness and/or uncertainty from the learner’s, as well as the teacher’s point of view. In 1999 Voskoglou [10] developed a fuzzy model for the description of the process of learning a subject matter in the classroom in terms of the possibilities of the student profiles and later he assessed the student learning skills by calculating the corresponding system’s total possibilistic uncertainty [11]. Meanwhile, Subbotin et al. [1], based on Voskoglou’s model [10], adapted properly the frequently used in fuzzy mathematics Center of Gravity (COG) defuzzification technique and used it as an alternative assessment method of student learning skills. Since then, Voskoglou and Subbotin, working either jointly or independently, applied the COG technique and a number of variations of it for assessing several human or machine (Decision – Making, Case-Based Reasoning, etc.) skills, e.g. see [2-7, 12-16], etc. In the present paper the outcomes of the COG technique and its variations are compared to the corresponding outcomes of a traditional assessment method of the bi-valued logic, the Grade Point Average (GPA) index. The rest of the paper is formulated as follows: In Section 2 we describe the classical GPA assessment method. In Section 3 we sketch the use of the COG technique as an assessment method, while in Section 4 we briefly describe the variations of the COG technique constructed in earlier papers and the reasons who led to the development of these variations. In Section 5 the outcomes of the COG technique and its variations are compared to the outcomes of the GPA index and examples are presented to illustrate our results. The last Section 6 is devoted to our conclusion and a discussion on the perspectives for future research on the subject.
2. Traditional Assessment Methods
- The assessment methods which are commonly used in practice are based on principles of the bi-valued logic. The calculation of the mean value of the scores achieved by each one of its members is the classical method for assessing the mean performance of a group of objects (e.g. students, players, machines, etc.) with respect to an action.On the other hand, a very popular in the USA and other Western countries assessment method is the calculation of the Grade Point Average (GPA) index. This index is a weighted average in which greater coefficients (weights) are assigned to the higher scores. GPA, which is connected to the quality group’s performance, is calculated by the formula
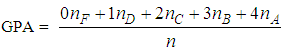 | (1) |
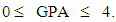 Consequently, values of GPA greater than 2 indicate a more than satisfactory performance.Finally note that formula (1) can be also written in the form
Consequently, values of GPA greater than 2 indicate a more than satisfactory performance.Finally note that formula (1) can be also written in the form 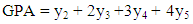 | (2) |
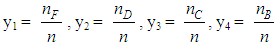 and
and 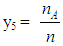 denote the frequencies of the group’s members which demonstrated unsatisfactory, fair, good, very good and excellent performance respectively.
denote the frequencies of the group’s members which demonstrated unsatisfactory, fair, good, very good and excellent performance respectively.3. The COG Defuzzification Technique as an Assessment Method (RFAM)
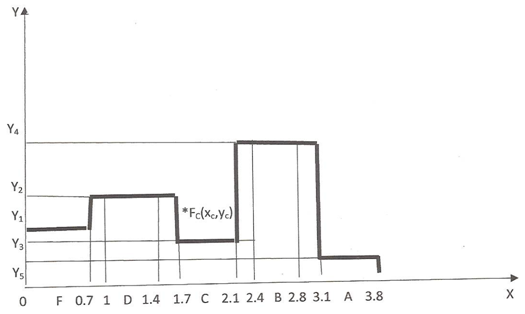
- The solution of a problem in terms of FL involves in general the following steps: Ÿ Choice of the universal set U of the discourse.Ÿ Fuzzification of the problem’s data by defining the proper membership functions.Ÿ Evaluation of the fuzzy data by applying rules and principles of FL to obtain a unique fuzzy set, which determines the required solution.Ÿ Defuzzification of the final outcomes in order to apply the solution found in terms of FL to the original, real world problem. One of the most popular in fuzzy mathematics defuzzification methods is the Centre of Gravity (COG) technique. For applying this method, let us assume that A = {(x, m(x)): x∈U} is the final fuzzy set determining the problem’s solution. We correspond to each x∈U an interval of values from a prefixed numerical distribution, which actually means that we replace U with a set of real intervals. Then, we construct the graph of the membership function y=m(x) and we consider the level’s area F contained between this graph and the OX axis. There is a commonly used in FL approach (e.g. see [9]) to represent the system’s fuzzy data by the coordinates (xc, yc) of the COG, say Fc, of the area F, which we calculate using the following well-known [19] from Mechanics formulas:
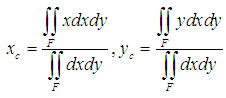 | (3) |
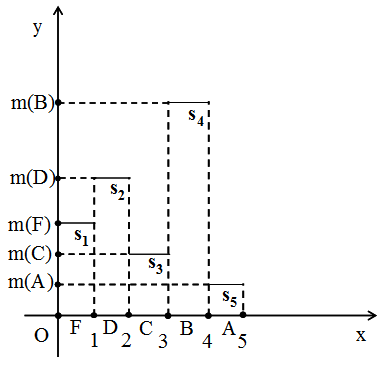 | Figure 1. The graph of the COG method |
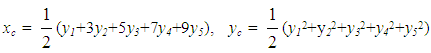 | (4) |
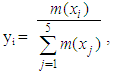 i = 1, 2, 3, 4, 5. Note that the membership function y = m(x), as it usually happens with fuzzy sets, can be defined, according to the user’s choice, in any compatible to the common logic way. However, in order to obtain assessment results compatible to the corresponding results of the GPA index, we define here y = m(x) in terms of the frequencies, as in formula (2) of Section 2. Then
i = 1, 2, 3, 4, 5. Note that the membership function y = m(x), as it usually happens with fuzzy sets, can be defined, according to the user’s choice, in any compatible to the common logic way. However, in order to obtain assessment results compatible to the corresponding results of the GPA index, we define here y = m(x) in terms of the frequencies, as in formula (2) of Section 2. Then 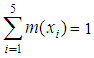 (100%).Using elementary algebraic inequalities and performing elementary geometric observations (e.g. Section 3 of [12]) one obtains the following assessment criterion: Ÿ Among two or more groups the group with the biggest xc performs better.Ÿ If two or more groups have the same xc 2.5, then the group with the higher yc performs better.Ÿ If two or more groups have the same xc < 2.5, then the group with the lower yc performs better.As it becomes evident from the above statement, a group’s performance depends mainly on the value of the x-coordinate of the COG of the corresponding level’s area, which is calculated by the first of formulas (4). In this formula, greater coefficients (weights) are assigned to the higher grades. Therefore, the COG method focuses, similarly to the GPA index, on the group’s quality performance. In case of the ideal performance (y5 =1 and yi = 0 for i5) the first of formulas (4) gives that
(100%).Using elementary algebraic inequalities and performing elementary geometric observations (e.g. Section 3 of [12]) one obtains the following assessment criterion: Ÿ Among two or more groups the group with the biggest xc performs better.Ÿ If two or more groups have the same xc 2.5, then the group with the higher yc performs better.Ÿ If two or more groups have the same xc < 2.5, then the group with the lower yc performs better.As it becomes evident from the above statement, a group’s performance depends mainly on the value of the x-coordinate of the COG of the corresponding level’s area, which is calculated by the first of formulas (4). In this formula, greater coefficients (weights) are assigned to the higher grades. Therefore, the COG method focuses, similarly to the GPA index, on the group’s quality performance. In case of the ideal performance (y5 =1 and yi = 0 for i5) the first of formulas (4) gives that 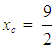 . Therefore, values of xc greater than
. Therefore, values of xc greater than 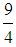 = 2.25 demonstrate a more than satisfactory performance.Due to the shape of the corresponding graph (Figure 1) the above method was named as the Rectangular Fuzzy Assessment Model (RFAM).
= 2.25 demonstrate a more than satisfactory performance.Due to the shape of the corresponding graph (Figure 1) the above method was named as the Rectangular Fuzzy Assessment Model (RFAM).4. Variations of the COG Technique (GRFAM, TFAM and TpFAM)
- A group’s performance is frequently represented by numerical scores in a climax from 0-100. These scores can be connected to the linguistic labels of U as follows: A (85-100), B(75-84), C (60-74), D(50-59) and F (0-49)1.Ambiguous cases appear in practice, being at the boundaries between two successive assessment grades; e.g. something like 84-85%, being at the boundaries between A and B. In an effort to treat better such kind of cases, Subbotin [4] “moved” the rectangles of Figure 1 to the left, so that to share common parts (see Figure 2). In this way, the ambiguous cases, being at the common rectangle parts, belong to both of the successive grades, which means that these parts must be considered twice in the corresponding calculations.
 | Figure 2. Graphical representation of the GRFAM |
 (100%).2. We take the heights of the rectangles in Figure 2 to have lengths equal to the corresponding frequencies. Also, without loss of generality we allow the sides of the adjacent rectangles lying on the OX axis to share common parts with length equal to the 30% of their lengths, i.e. 0.3 units.23. We calculate the coordinates
(100%).2. We take the heights of the rectangles in Figure 2 to have lengths equal to the corresponding frequencies. Also, without loss of generality we allow the sides of the adjacent rectangles lying on the OX axis to share common parts with length equal to the 30% of their lengths, i.e. 0.3 units.23. We calculate the coordinates 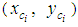 of the COG, say Fi , of each rectangle, i = 1, 2, 3, 4, 5 as follows: Since the COG of a rectangle is the point of the intersection of its diagonals, we have that
of the COG, say Fi , of each rectangle, i = 1, 2, 3, 4, 5 as follows: Since the COG of a rectangle is the point of the intersection of its diagonals, we have that 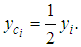 Also, since the x-coordinate of each COG Fi is equal to the x- coordinate of the middle of the side of the corresponding rectangle lying on the OX axis, from Figure 2 it is easy to observe that
Also, since the x-coordinate of each COG Fi is equal to the x- coordinate of the middle of the side of the corresponding rectangle lying on the OX axis, from Figure 2 it is easy to observe that 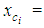
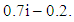 4. We consider the system of the COGs Fi and we calculate the coordinates (Xc, Yc) of the COG F of the whole area considered in Figure 2 as the resultant of the system of the GOCs Fi of the five rectangles from the following well known [20] formulas
4. We consider the system of the COGs Fi and we calculate the coordinates (Xc, Yc) of the COG F of the whole area considered in Figure 2 as the resultant of the system of the GOCs Fi of the five rectangles from the following well known [20] formulas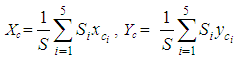 | (5) |
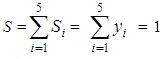 and formulas (5) give that
and formulas (5) give that  or
or 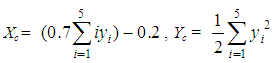 | (6) |
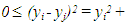
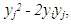 therefore
therefore 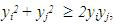 with the equality holding if, and only if, yi = yj. Therefore
with the equality holding if, and only if, yi = yj. Therefore 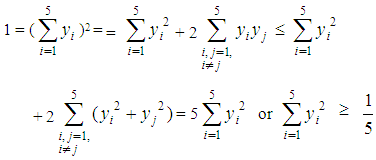 | (7) |
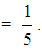 In case of the equality the first of formulas (6) gives that
In case of the equality the first of formulas (6) gives that 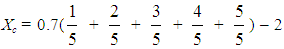 = 1.9. Further, combining the inequality (7) with the second of formulas (6), one finds that
= 1.9. Further, combining the inequality (7) with the second of formulas (6), one finds that 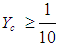 Therefore the unique minimum for Yc corresponds to the COG Fm (1.9, 0.1). The ideal case is when y1 = y2 = y3 = y4 = 0 and y5=1. Then formulas (2) give that Xc = 3.3 and
Therefore the unique minimum for Yc corresponds to the COG Fm (1.9, 0.1). The ideal case is when y1 = y2 = y3 = y4 = 0 and y5=1. Then formulas (2) give that Xc = 3.3 and 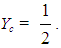 Therefore the COG in this case is the point Fi (3.3, 0.5). On the other hand, the worst case is when y1 = 1 and y2 = y3 = y4 = y5 = 0. Then from formulas (2) we find that the COG is the point Fw (0.5, 0.5). Therefore, the area in which the COG F lies is the area of the triangle Fw Fm Fi (Figure 3).
Therefore the COG in this case is the point Fi (3.3, 0.5). On the other hand, the worst case is when y1 = 1 and y2 = y3 = y4 = y5 = 0. Then from formulas (2) we find that the COG is the point Fw (0.5, 0.5). Therefore, the area in which the COG F lies is the area of the triangle Fw Fm Fi (Figure 3). 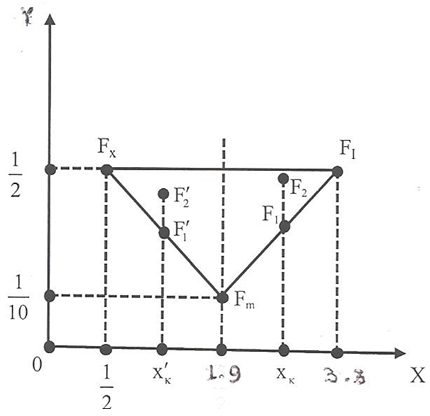 | Figure 3. The triangle where the COG lies |
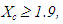 then the group with the greater Yc performs better.Ÿ If two groups have the same
then the group with the greater Yc performs better.Ÿ If two groups have the same 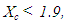 then the group with the lower Yc performs betterFrom the first of formulas (6) it becomes evident that the GRFAM measures the quality group’s performance. Also, since the ideal performance corresponds to the value Xc = 3.3, values of Xc greater than
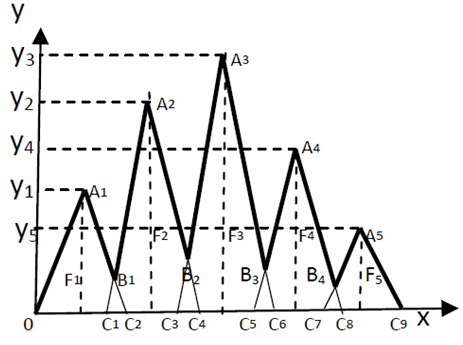
then the group with the lower Yc performs betterFrom the first of formulas (6) it becomes evident that the GRFAM measures the quality group’s performance. Also, since the ideal performance corresponds to the value Xc = 3.3, values of Xc greater than 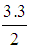 = 1.65 indicate a more than satisfactory performance.At this point one could raise the following question: Does the shape of the membership function’s graph of the assessment model affect the assessment’s conclusions? For example, what will happen if the rectangles of the GRFAM will be replaced by isosceles triangles? The effort to answer this question led to the construction of the Triangular Fuzzy Assessment Model (TFAM), created by Subbotin & Bilotskii [2] and fully developed by Subbotin & Voskoglou [3]. The graphical representation of TFAM is shown in Figure 4 and the steps followed for its development are the same with the corresponding steps of GRFAM presented above. The only difference is that one works with isosceles triangles instead of rectangles. The final formulas calculating the coordinates of the COG of TFAM are:
= 1.65 indicate a more than satisfactory performance.At this point one could raise the following question: Does the shape of the membership function’s graph of the assessment model affect the assessment’s conclusions? For example, what will happen if the rectangles of the GRFAM will be replaced by isosceles triangles? The effort to answer this question led to the construction of the Triangular Fuzzy Assessment Model (TFAM), created by Subbotin & Bilotskii [2] and fully developed by Subbotin & Voskoglou [3]. The graphical representation of TFAM is shown in Figure 4 and the steps followed for its development are the same with the corresponding steps of GRFAM presented above. The only difference is that one works with isosceles triangles instead of rectangles. The final formulas calculating the coordinates of the COG of TFAM are: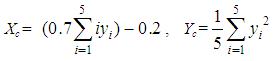 | (8) |
 | Figure 4. Graphical Representation of the TFAM |
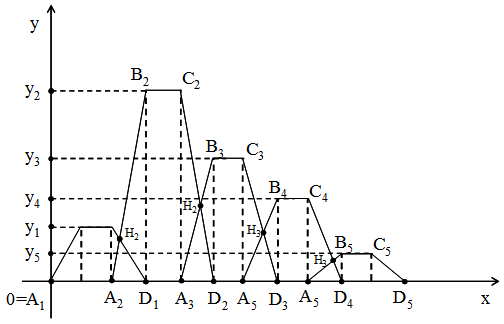 | Figure 5. The TpFAM’s scheme |
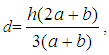 where h is its height [18]. Also, since the x-coordinate of the COG of each trapezoid is equal to the x-coordinate of the midpoint of its base, it is easy to observe from Figure 5 that x = 0.7i - 0.2.One finally obtains from formulas (5) that
where h is its height [18]. Also, since the x-coordinate of the COG of each trapezoid is equal to the x-coordinate of the midpoint of its base, it is easy to observe from Figure 5 that x = 0.7i - 0.2.One finally obtains from formulas (5) that 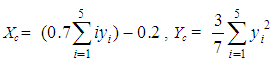 | (9) |
5. Comparison of the Assessment Methods
- One can write formulas (6), (8) and (9) of Section 4 in the single form:
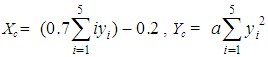 | (10) |
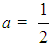 for the GRFAM,
for the GRFAM, 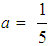 for the TFAM and
for the TFAM and 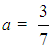 for the TpFAM. Combining formulas (10) with the common assessment criterion stated in Section 4 one obtains the following result:
for the TpFAM. Combining formulas (10) with the common assessment criterion stated in Section 4 one obtains the following result:5.1. Theorem
- The three variations of the COG technique, i.e. the GRFAM, the TFAM and the TpFAM are equivalent assessment models.Further, the first of formulas (10) can be written as
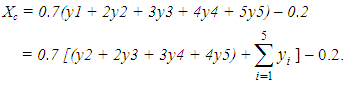 Therefore, by formula (2) of Section 3, one finally gets that
Therefore, by formula (2) of Section 3, one finally gets that 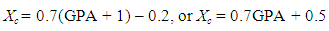 | (11) |
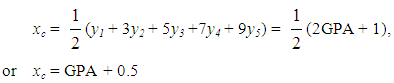 | (12) |
5.2. Theorem
- If the values of the GPA index are different for two groups, then the GPA index, the RFAM and its variations (GRFAM, TFAM and TpFAM) provide the same assessment outcomes on comparing the performance of these groups.Proof: Let G and G΄ be the values of the GPA index for the two groups and let xc, xc΄ be the corresponding values of the x-coordinate of the COG for the RFAM. Assume without loss of generality that G>G΄, i.e. that the first group performs better according to the GPA index. Then, equation (12) gives that
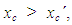 which, according to the first case of the assessment criterion of Section 3, shows that the first group performs also better according to the RFAM.In the same way, from equation (11) and the first case of the assessment criterion of Section 4, one finds that the first group performs better too according to the equivalent assessment models GRFAM, TFAM and TpFAM.In case of the same GPA index we shall show the following result:
which, according to the first case of the assessment criterion of Section 3, shows that the first group performs also better according to the RFAM.In the same way, from equation (11) and the first case of the assessment criterion of Section 4, one finds that the first group performs better too according to the equivalent assessment models GRFAM, TFAM and TpFAM.In case of the same GPA index we shall show the following result:5.3. Theorem
- If the GPA index is the same for two groups then the RFAM and its variations (GRFAM, TFAM and TpFAM) provide the same assessment outcomes on comparing the performance of these groups.Proof: Since the two groups possess the same value of the GPA index, equations (11) and (12) show that the values of Xc and xc are also the same. Therefore, one of the last two cases of the assessment criteria of Sections 3 and 4 could happen. The possible values of x in these criteria lie in the intervals
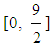 and [0, 3.3] respectively, while the critical points correspond to the values xc = 2.5 and Xc = 1.9 respectively. Obviously, if both values of x are in [0, 1.9), or in
and [0, 3.3] respectively, while the critical points correspond to the values xc = 2.5 and Xc = 1.9 respectively. Obviously, if both values of x are in [0, 1.9), or in 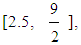 then the two criteria provide the same assessment outcomes on comparing the performance of the two groups. Assume therefore that 1.9 < Xc and xc < 2.5. Then, due to equation (11), 1.9 < Xc
then the two criteria provide the same assessment outcomes on comparing the performance of the two groups. Assume therefore that 1.9 < Xc and xc < 2.5. Then, due to equation (11), 1.9 < Xc  1.9< 0.7GPA + 0.5
1.9< 0.7GPA + 0.5  1.4 <0.7GPA
1.4 <0.7GPA  GPA > 2. Also, due to equation (12), xc < 2.5
GPA > 2. Also, due to equation (12), xc < 2.5  GPA + 0.5 < 2.5
GPA + 0.5 < 2.5  GPA > 2. Therefore, the inequalities 1.9 < Xc and xc < 2.5 cannot hold simultaneously and the result follows.-Combining Theorems 5.2 and 5.3 one obtains the following corollary:
GPA > 2. Therefore, the inequalities 1.9 < Xc and xc < 2.5 cannot hold simultaneously and the result follows.-Combining Theorems 5.2 and 5.3 one obtains the following corollary:5.4. Corollary
- The RFAM and its variations GRFAM, TFAM and TpFAM provide always the same assessment results on comparing the performance of two groups.The following example shows that in case of the same GPA values the application of the GPA index could not lead to logically based conclusions (see also paragraph (vii) of Section 4 of [7]). Therefore, in such situations, our criteria of Sections 3 and 4 become useful due to their logical nature.
5.5. Example
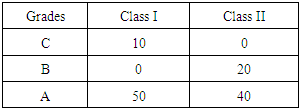
- The student grades of two Classes with 60 students in each Class are presented in Table 1
|
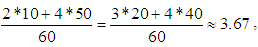 which means that the two Classes demonstrate the same performance in terms of the GPA index. Therefore equation (11) gives that Xc = 0.7*3.67 + 0.5
which means that the two Classes demonstrate the same performance in terms of the GPA index. Therefore equation (11) gives that Xc = 0.7*3.67 + 0.5 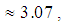 while equation (12) gives that xc = 4.17 for both Classes. But
while equation (12) gives that xc = 4.17 for both Classes. But 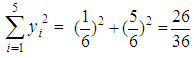 for the first and
for the first and 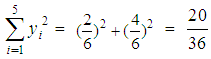 for the second Class. Therefore, according to the assessment criteria of Sections 3 and 4 the first Class demonstrates a better performance in terms of the RFAM and its variations. Now which one of the above two conclusions is closer to the reality? For answering this question, let us consider the quality of knowledge, i.e. the ratio of the students received B or better to the total number of students, which is equal to
for the second Class. Therefore, according to the assessment criteria of Sections 3 and 4 the first Class demonstrates a better performance in terms of the RFAM and its variations. Now which one of the above two conclusions is closer to the reality? For answering this question, let us consider the quality of knowledge, i.e. the ratio of the students received B or better to the total number of students, which is equal to 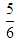 for the first and 1 for the second Class. Therefore, from the common point of view, the situation in Class II is better. However, many educators could prefer the situation in Class I having a greater number of excellent students. Conclusively, in no case it is logical to accept that the two Classes demonstrated the same performance, as the calculation of the GPA index suggests.The next example shows that although the RFAM, GRFAM, TFAM and TpFAM provide always the same assessment results on comparing the performance of two groups (Corollary 5.4), they are not equivalent assessment models.
for the first and 1 for the second Class. Therefore, from the common point of view, the situation in Class II is better. However, many educators could prefer the situation in Class I having a greater number of excellent students. Conclusively, in no case it is logical to accept that the two Classes demonstrated the same performance, as the calculation of the GPA index suggests.The next example shows that although the RFAM, GRFAM, TFAM and TpFAM provide always the same assessment results on comparing the performance of two groups (Corollary 5.4), they are not equivalent assessment models. 5.6. Example
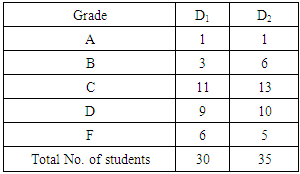
- Table 2 depicts the results of the final exams of the first term mathematical courses of two different Departments, say D1 and D2, of the School of Technological Applications (future engineers) of the Graduate T. E. I. of Western Greece. Note that the contents of the two courses and the instructor were the same for the two Departments.
|
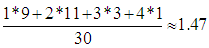 for D1 and
for D1 and 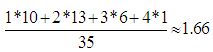 for D2. Therefore, the two Departments demonstrated a less than satisfactory performance (since GPA < 2), with the performance of D2 being better.Further, equation (11) gives that Xc1.53 for D1 and Xc1.66 for D2. Therefore, according to the first case of the assessment criterion of Section 4, D2 demonstrated (with respect to GRFAM, TFAM and TpFAM) a better performance than D1. Moreover, since
for D2. Therefore, the two Departments demonstrated a less than satisfactory performance (since GPA < 2), with the performance of D2 being better.Further, equation (11) gives that Xc1.53 for D1 and Xc1.66 for D2. Therefore, according to the first case of the assessment criterion of Section 4, D2 demonstrated (with respect to GRFAM, TFAM and TpFAM) a better performance than D1. Moreover, since 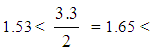
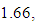 D1 demonstrated a less than satisfactory performance, while D2 demonstrated a more than satisfactory performance.In the same way equation (12) gives that xc1.97 for D1 and xc2.16 for D2. Therefore, according to the first case of the assessment criterion of Section 3, D2 demonstrated (with respect to RFAM) a better performance than D1. But in this case, since for both Departments
D1 demonstrated a less than satisfactory performance, while D2 demonstrated a more than satisfactory performance.In the same way equation (12) gives that xc1.97 for D1 and xc2.16 for D2. Therefore, according to the first case of the assessment criterion of Section 3, D2 demonstrated (with respect to RFAM) a better performance than D1. But in this case, since for both Departments 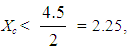 the two Departments demonstrated a less than satisfactory performance.REMARK: Note that, if GPA > 2 (more than satisfactory performance), then Xc = 0.7GPA + 0.5 > 0.7 * 2 + 0.5 = 1.9 > 1.65 and xc = GPA + 0.5 > 0.2 + 0.5 = 2.5> 2.25. Therefore the corresponding group’s performance is also more than satisfactory with respect to GRFAM, TFAM, TpFAM and RFAM. However, if GPA < 2 (less than satisfactory performance), then Xc < 1.9 and xc < 2.5, which do not guarantee that Xc < 1.65 and xc < 2.25. Therefore the assessment characterizations of RFAM and the equivalent GRFAM, TFAM, TpFAM can be different only when GPA < 2.
the two Departments demonstrated a less than satisfactory performance.REMARK: Note that, if GPA > 2 (more than satisfactory performance), then Xc = 0.7GPA + 0.5 > 0.7 * 2 + 0.5 = 1.9 > 1.65 and xc = GPA + 0.5 > 0.2 + 0.5 = 2.5> 2.25. Therefore the corresponding group’s performance is also more than satisfactory with respect to GRFAM, TFAM, TpFAM and RFAM. However, if GPA < 2 (less than satisfactory performance), then Xc < 1.9 and xc < 2.5, which do not guarantee that Xc < 1.65 and xc < 2.25. Therefore the assessment characterizations of RFAM and the equivalent GRFAM, TFAM, TpFAM can be different only when GPA < 2.6. Conclusions and Perspectives for Future Research
- From the discussion performed in this paper it becomes evident that the RFAM and its variations GRFAM, TFAM and TpFAM, although they provide always the same assessment outcomes on comparing the performance of two groups, they are not equivalent assessment methods. The above assessment outcomes are also the same with those of the GPA index, unless if the groups under assessment possess the same values. In the last case the GPA index could not lead to logically based conclusions. Therefore, in this case either the use of RFAM or of its variations must be preferred. Other fuzzy assessment methods have been also used in earlier author’s works like the measurement of a system’s uncertainty [11] and the application of the fuzzy numbers [17]. These methods, in contrast to the previous ones which focus on the corresponding group’s quality performance, they measure its mean performance. The plans for our future research include the effort to compare all these methods in order to obtain the analogous conclusions.
Notes
- 1. This way of connection, although it satisfies the common sense, it is not unique; in a more strict assessment, for example, one could take A(90-100), B(80-89), C(70-79), D(60-69) and F (0-59), etc.2. Since the ambiguous assessment cases are situated at the boundaries between the adjacent grades, it is logical to accept a percentage for the common lengths of less than 50%.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML