-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(5): 182-186
doi:10.5923/j.ajcam.20160605.02

On Extracting Properties of Lie Groups from Their Lie Algebras
1Department of Mathematics, Faculty of Science and Arts – Khulais, University of Jeddah, Saudi Arabia
2Department of Mathematics, Faculty of Education, Alzaeim Alazhari University (AAU), Khartoum, Sudan
Correspondence to: M-Alamin A. H. Ahmed, Department of Mathematics, Faculty of Science and Arts – Khulais, University of Jeddah, Saudi Arabia.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The study of Lie groups and Lie algebras is very useful, for its wider applications in various scientific fields. In this paper, we introduce a thorough study of properties of Lie groups via their lie algebras, this is because by using linearization of a Lie group or other methods, we can obtain its Lie algebra, and using the exponential mapping again, we can convey properties and operations from the Lie algebra to its Lie group. These relations helpin extracting most of the properties of Lie groups by using their Lie algebras. We explain this extraction of properties, which helps in introducing more properties of Lie groups and leads to some important results and useful applications. Also we gave some properties due to Cartan’s first and second criteria.
Keywords: Lie group, Lie algebra, Exponential mapping, Linearization Killing form, Cartan’s criteria
Cite this paper: M-Alamin A. H. Ahmed, On Extracting Properties of Lie Groups from Their Lie Algebras, American Journal of Computational and Applied Mathematics , Vol. 6 No. 5, 2016, pp. 182-186. doi: 10.5923/j.ajcam.20160605.02.
Article Outline
1. Introduction
- The Properties and applications of Lie groups and their Lie algebras are too great to overview in a small paper. Lie groups were greatly studied by Marius Sophus Lie (1842 – 1899), who intended to solve or at least to simplify ordinary differential equations, and since then the research continues to disclose their properties and applications in various scientific fields [1, 2, 5, 6]. Lie groups have algebraic properties derived from their group axioms, and geometric properties due to identification of their group operations with points in a topological space, namely every Lie group is a differentiable manifold [3, 4, 7]. Almost all of the Lie groups encountered in many applications are matrix groups, and this simplifies their study. This simplification can be done by linearizing the Lie group in the neighborhood of its identity, which results in what is called a Lie algebra [1]. The Lie algebra retains most of, but not all of the properties of the original Lie group. Also most of the Lie group properties can be recovered by the inverse of the linearization operation, namely, the exponential mapping. A Lie algebra is a linear vector space, and this makes it easy to study it by using tools of linear algebra rather than studying the original Lie group with its complicated structure. In this manner we can extract properties of a Lie group from its Lie algebra, and this opens the door to many scientific applications, for instance in mathematics and physics.
2. Lie Group
2.1. Definition (Lie group)
- A Lie group
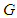 is an abstract group and a smooth n-dimensional manifold so that multiplication
is an abstract group and a smooth n-dimensional manifold so that multiplication 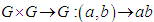 and inverse
and inverse 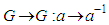 are smooth.
are smooth.2.2. Examples
- a) The general linear group
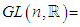
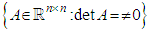 is an open set of
is an open set of 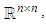 it is a manifold with the two operations, matrix multiplication and matrix inverse which are
it is a manifold with the two operations, matrix multiplication and matrix inverse which are 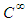 mappings. So it is a Lie group. b) The complex linear group
mappings. So it is a Lie group. b) The complex linear group 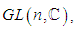 the group of nonsingular
the group of nonsingular 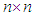 matrices is also a Lie group.c) We can take the two subsets of the general linear group: the special linear group
matrices is also a Lie group.c) We can take the two subsets of the general linear group: the special linear group 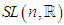 which is the group of matrices of determinant 1 and the other is the orthogonal group
which is the group of matrices of determinant 1 and the other is the orthogonal group 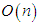 consisting of all matrices
consisting of all matrices 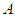 satisfying
satisfying 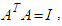 these two subsets are also Lie groups.Matrix groups are very important examples of Lie groups because of their various scientific applications. There are many examples of Lie groups different from matrix groups.
these two subsets are also Lie groups.Matrix groups are very important examples of Lie groups because of their various scientific applications. There are many examples of Lie groups different from matrix groups.3. Lie Algebra
3.1. Definition (Lie Algebra)
- A Lie algebra over a field K
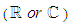 is a vector space
is a vector space 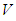 over K with a skew – symmetric k- bilinear form (the Lie bracket)
over K with a skew – symmetric k- bilinear form (the Lie bracket) 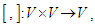 which satisfies the Jacobi identity:
which satisfies the Jacobi identity: 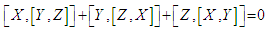 | (3.1) |
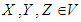 The tangent space
The tangent space 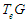 at the identity of a Lie group canonically has the structure of Lie algebra. This Lie algebra encodes in it much information about the Lie group. So we have to define the Lie algebra structure on
at the identity of a Lie group canonically has the structure of Lie algebra. This Lie algebra encodes in it much information about the Lie group. So we have to define the Lie algebra structure on 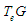 and this can be shown if we identified this structure with the Lie algebra for instance for some classical groups.
and this can be shown if we identified this structure with the Lie algebra for instance for some classical groups.3.2. Example
- Since
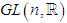 is an open subset of
is an open subset of 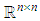 (the vector space of all
(the vector space of all 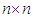 real matrices), the tangent space to
real matrices), the tangent space to 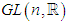 at the identity
at the identity 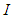 is
is 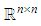 itself.Also the tangent space
itself.Also the tangent space 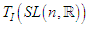 is the subspace of
is the subspace of 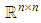 consisting of all
consisting of all 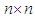 matrices of trace 0.And for the group of orthogonal matrices
matrices of trace 0.And for the group of orthogonal matrices 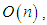 the tangent space at the identity is consisting of skew – symmetric matrices. These are some examples of Lie algebras of some groups of matrices considered as tangent spaces at the identity.
the tangent space at the identity is consisting of skew – symmetric matrices. These are some examples of Lie algebras of some groups of matrices considered as tangent spaces at the identity. 4. Linearization of a Lie Group
- The Lie group may have a complicated structure which make it difficult to study it through some mathematical tools, instead of this we linearize the group in the neighborhood of its identity, that is by getting a vector space at the identity, this vector space is its Lie algebra. Therefore, Linearization of Lie group makes it possible to study it by using tools of Linear algebra. Moreover most of the Lie group properties can be recovered by the inverse of the linearization operation, that is by the exponential mapping. The following diagram expresses how to go from the Lie group to its Lie algebra and vice versa by using these two operations:
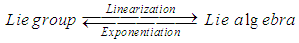
4.1. How To Linearize a Lie Group?
- In order to linearize a Lie group to get its Lie algebra we need an explicit parametrization of the underlying manifold and also we need an available expression for the group composition law. For matrix groups the group composition law is matrix multiplication and every matrix group is a closed subset of the general linear group, so we can do linearization immediately as we see in the following example:
4.2. Example
- To linearize the Lie group
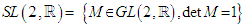 We parametrize the group by:
We parametrize the group by: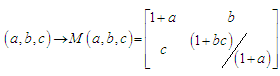 | (4.1) |
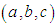 to become infinitesimals:
to become infinitesimals: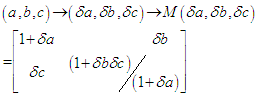 | (4.2) |
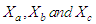 are the coefficients of the first order infinitesimals:
are the coefficients of the first order infinitesimals: 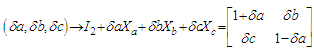 | (4.3) |
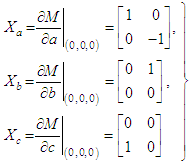 | (4.4) |
 in our example.
in our example.5. Exponential Mapping
- Suppose
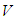 is a finite dimensional vector space equipped with a complete norm
is a finite dimensional vector space equipped with a complete norm 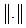 over the field
over the field 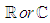 . If
. If  denotes the algebra of linear automorphisms on
denotes the algebra of linear automorphisms on 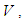 and
and 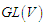 the general linear group. Then for
the general linear group. Then for 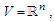
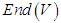 is identified with
is identified with 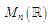 (
(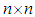 matrices ) and
matrices ) and 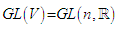 .
.5.1. Definition (Matrix Group)
- A matrix group is a closed subgroup of
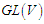 (the general linear group), where
(the general linear group), where 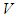 is a finite dimensional vector space.
is a finite dimensional vector space.5.2. Definition (Exponential map)
- The exponential map on
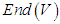 is defined by
is defined by 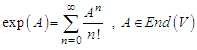 | (5.1) |
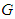 is a Lie group with Lie algebra
is a Lie group with Lie algebra 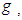 then the exponential map is defined as:
then the exponential map is defined as: 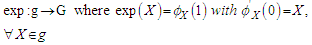
5.3. Definition (One – Parameter Subgroup)
- A one – parameter subgroup of a Lie group
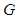 is a continuous homomorphism:
is a continuous homomorphism: 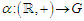
5.4. Example
- For the Lie groups
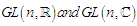 , we have
, we have 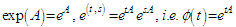 is a one parameter group. Furthermore
is a one parameter group. Furthermore 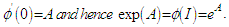
5.5. Proposition [2]
- For
 a finite dimensional normed vector space and
a finite dimensional normed vector space and 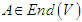 , the map
, the map 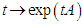 is a one – parameter subgroup of
is a one – parameter subgroup of 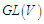 . In particular
. In particular 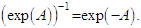
5.6. Theorem [2]
- Every one – parameter subgroup
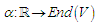 is of the form
is of the form 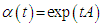 for some
for some 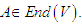
5.7. Definition (The Infinitesimal Generator)
- The element
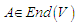 is called the infinitesimal generator of the one – parameter subgroup
is called the infinitesimal generator of the one – parameter subgroup 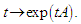
5.8. Lemma
- The exponential map is absolutely convergent, hence convergent on all of
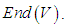 Hence it defines an analytic automorphism on
Hence it defines an analytic automorphism on 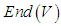 .Proof
.Proof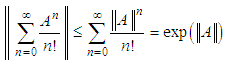
5.9. Lemma [2]
- The identity map on
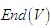 is the derivative at 0 of
is the derivative at 0 of 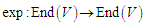 that is,
that is, 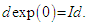
5.10. Theorem (The Lie Algebra of a Matrix Group)
- For a matrix group
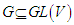 , the set
, the set 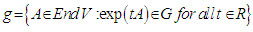 is a Lie algebra, called the Lie algebra of
is a Lie algebra, called the Lie algebra of 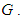 Sketch of the Proof:The theorem can be proved by showing that:
Sketch of the Proof:The theorem can be proved by showing that: 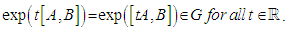 Thus the commutator
Thus the commutator 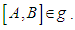
5.11. Computing Lie Algebras
- For matrix groups we can use some methods to find their Lie algebras. For instance we can use the following proposition for this purpose.
5.12. Proposition
- Let
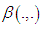 be a continuous bilinear form on the vector space
be a continuous bilinear form on the vector space 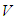 and set
and set 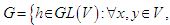
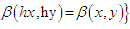 , then the Lie algebra is
, then the Lie algebra is 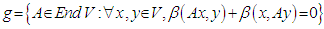 .ProofLet
.ProofLet 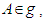 then
then 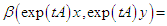
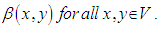 Differentiating with respect to t:
Differentiating with respect to t: 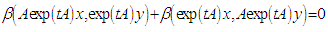 , then at
, then at 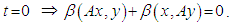 Conversely: for all
Conversely: for all 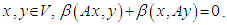 Then for
Then for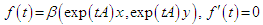 , therefore
, therefore 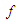 is constant function of a value
is constant function of a value 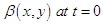 . It follows that:
. It follows that: 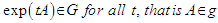
6. Exponentiation
- We can reverse the linearization operation by using the exponential map so as to recover most of the properties of the Lie group from its Lie algebra. We can see the behavior of elements near the identity of the Lie group. Suppose
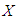 is an operator in a Lie algebra, and let
is an operator in a Lie algebra, and let 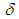 be a small real number. Then
be a small real number. Then  represents an element in the Lie group close to the identity. Far from the identity by iterating this group operation many times we get the exponential function:
represents an element in the Lie group close to the identity. Far from the identity by iterating this group operation many times we get the exponential function: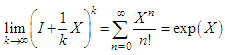 | (6.1) |
6.1. Example
- On taking the Lie group
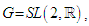 we can show how to exponentiate an operator in its Lie algebra to get the result in the group
we can show how to exponentiate an operator in its Lie algebra to get the result in the group 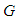 as follows:given the basis vectors
as follows:given the basis vectors 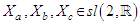 (the Lie algebra), let us take the operator
(the Lie algebra), let us take the operator 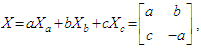 then
then 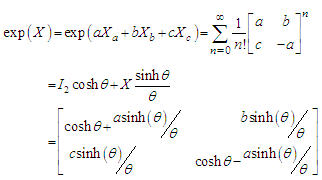 | (6.2) |
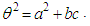 In fact
In fact 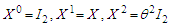 so
so 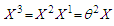 is proportional to
is proportional to 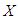 and
and 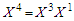 is proportional to the identity and so on.We can put
is proportional to the identity and so on.We can put 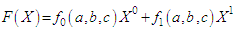 where
where 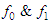 are functions of the invariants of the matrix, that is
are functions of the invariants of the matrix, that is 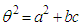 (Cayley – Hamilton theorem).So that
(Cayley – Hamilton theorem).So that 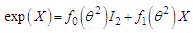 | (6.3) |
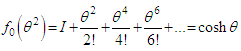 | (6.4) |
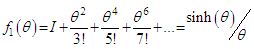 | (6.5) |
7. Isomorphism on Lie Groups and Lie Algebras
- Isomorphic Lie groups have isomorphic Lie algebras, but, two Lie groups with isomorphic Lie algebras need not be isomorphic as we see in the following example.
7.1. Example
- The groups
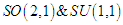 have respectively the Lie algebras
have respectively the Lie algebras 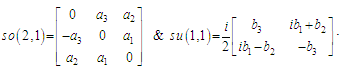 The Lie algebras are isomorphic because there is a 1:1 correspondence between them, but the groups have a 2:1 correspondence, that is why they are not isomorphic.
The Lie algebras are isomorphic because there is a 1:1 correspondence between them, but the groups have a 2:1 correspondence, that is why they are not isomorphic.8. Some Properties
8.1. Definition (Ideals and Simple Lie Algebras)
- An ideal I of a Lie algebra
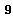 is a vector space of
is a vector space of 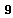 such that
such that 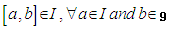 A simple Lie algebra is the one which has no proper ideal. Also a semisimple Lie algebra is the one which is a direct sum of simple Lie algebras.
A simple Lie algebra is the one which has no proper ideal. Also a semisimple Lie algebra is the one which is a direct sum of simple Lie algebras.8.2. Example
- Let
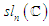 be the set of all
be the set of all 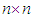 matrices of trace 0.
matrices of trace 0. 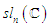 is an ideal of
is an ideal of 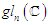 which is nonzero. So
which is nonzero. So 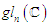 is not simple.
is not simple.8.3. Definition (The Adjoint Representation)
- Let
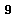 be a Lie algebra over k. A representation of
be a Lie algebra over k. A representation of 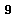 is a Lie algebra homomorphism
is a Lie algebra homomorphism 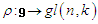 for some n called the degree of the representation. We define a mapping
for some n called the degree of the representation. We define a mapping 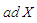 from a Lie algebra to itself by
from a Lie algebra to itself by 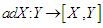 . The mapping
. The mapping 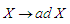 is a representation of the Lie algebra called the adjoint representation. It is an automorphism.
is a representation of the Lie algebra called the adjoint representation. It is an automorphism. 8.4. Cartan Subalgebra 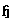
- A cartan subalgebra
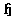 for a Lie algebra
for a Lie algebra 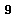 is an abelian, diagonalizable subalgebra which is maximal under set inclusion. Its dimension is the rank of
is an abelian, diagonalizable subalgebra which is maximal under set inclusion. Its dimension is the rank of 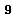 .All Cartan Lie algebras of a Lie algebra
.All Cartan Lie algebras of a Lie algebra 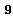 are conjugate under automorphisms of
are conjugate under automorphisms of 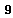 , and they have the same dimension. Define the basis
, and they have the same dimension. Define the basis 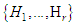 for
for 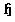 . Since
. Since 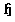 is abelian,
is abelian, 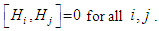 If we extend this basis for
If we extend this basis for 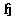 to a basis for
to a basis for 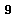 , and then we get a much simpler basis for
, and then we get a much simpler basis for 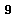 with convenient commutator relations. This can be used in many applications of Lie algebras, especially in classification machinery.
with convenient commutator relations. This can be used in many applications of Lie algebras, especially in classification machinery.8.5. The Killing Form
- For the Lie algebra g, if
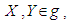 we define the Killing form by
we define the Killing form by 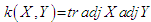 , it resembles a scalar product for elements of a Lie algebra itself. It is invariant under all automorphisms of g.The killing form is an effective tool in calculations in Lie algebra and symmetric spaces and in describing some properties due to some Cartan’s theorems.
, it resembles a scalar product for elements of a Lie algebra itself. It is invariant under all automorphisms of g.The killing form is an effective tool in calculations in Lie algebra and symmetric spaces and in describing some properties due to some Cartan’s theorems.8.6. Cartan’s First Criterion [8]
- A Lie algebra g is solvable if and only if its Killing form vanishes identically on the derived Lie algebra
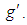 It is easy to see that both solvability and vanishing of the Killing form remain unchanged under complexification for a real Lie algebra g; thus we may take g complex.
It is easy to see that both solvability and vanishing of the Killing form remain unchanged under complexification for a real Lie algebra g; thus we may take g complex.8.7. Cartan’s Second Criterion [8]
- A Lie algebra g is semisimple if and only if its dimension is positive and its killing form is non-degenerate.(Non-degenerate means: If for some X0 in g the value of the killing form is 0 for all Y in g, then X0 is 0).Just as for the first criterion we may assume that g is complex, since both semisimplicity and non-degeneracy of the killing form are unchanged by complixification.
9. Conclusions
- 1. The exponential operation provides a natural parametrization of the Lie group in terms of linear quantities. This function maps the linear vector space – the Lie algebra – to the geometric manifold that parameterizes the Lie group.2. It is not always possible to map a Lie algebra onto the entire Lie group through a single mapping of the form exp(X).3. Since the exponential map takes elements of the Lie algebra to the geometric manifold that parametrizes the Lie group, we expect not to be able to extract all properties of the Lie group from its Lie algebra, but most of these properties can be retained.4. Since isomorphic Lie groups have isomorphic Lie algebras, research can go on studying joined properties of Lie groups using their isomorphic Lie algebras.5. The killing form is an effective tool in describing some important properties of the Lie algebra and in carrying some calculations on it.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML