T. Zhanlav1, V. Ulziibayar1, 2
1Institute of Mathematics, National University of Mongolia, Mongolia
2School of Applied Sciences, Mongolian University of Science and Technology, Mongolia
Correspondence to: V. Ulziibayar, Institute of Mathematics, National University of Mongolia, Mongolia.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, based on King's methods, a new family of eighth-order methods for solving nonlinear equations is derived. This family of methods includes method given in [9] as a particular case. The optimal choice of the iteration parameter allows us to accelerate and improve the convergence of iterations. At each iteration of these methods requires three evaluation of the function and one evaluation of its first derivative, which has optimal efficiency index 1.682, according to Kung and Traube's conjecture. Numerical comparisons are made to show the performance of the presented methods.
Keywords:
Nonlinear equations, Modified King's method, Convergence order, Efficiency index
Cite this paper: T. Zhanlav, V. Ulziibayar, Modified King's Methods with Optimal Eighth-order of Convergence and High Efficiency Index, American Journal of Computational and Applied Mathematics , Vol. 6 No. 5, 2016, pp. 177-181. doi: 10.5923/j.ajcam.20160605.01.
1. Introduction
In this work, we consider iterative methods to find a simple root 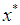 of a nonlinear equation
of a nonlinear equation 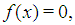 | (1) |
where 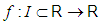 is a scalar function on the open interval
is a scalar function on the open interval 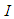 .The constructing of higher-order convergence methods has attracted a lot of attention from both theoretical as well as practical point of view, see for example [1-9] and references therein.King in [3] developed a one-parameter family of fourth-order methods, which is written as
.The constructing of higher-order convergence methods has attracted a lot of attention from both theoretical as well as practical point of view, see for example [1-9] and references therein.King in [3] developed a one-parameter family of fourth-order methods, which is written as 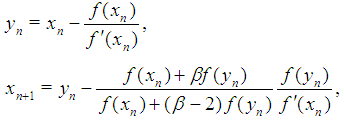 | (2) |
where 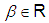 is a parameter. In particular, the famous Ostrowski’s method is a member of this family when
is a parameter. In particular, the famous Ostrowski’s method is a member of this family when 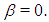 Recently, based on King’s or Ostrowski’s method, some optimal order iterative methods have been proposed and analyzed for solving nonlinear equations [1, 2, 5, 6, 8, 9]. In particular, Bi et al [1] presented a new family of eighth-order methods:
Recently, based on King’s or Ostrowski’s method, some optimal order iterative methods have been proposed and analyzed for solving nonlinear equations [1, 2, 5, 6, 8, 9]. In particular, Bi et al [1] presented a new family of eighth-order methods: 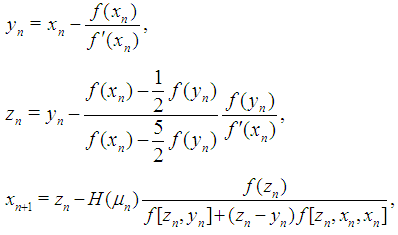 | (3) |
where  and
and 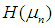 represents a real-valued function, satisfying the conditions
represents a real-valued function, satisfying the conditions 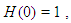
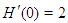 and
and 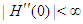 and divided differences are denoted by
and divided differences are denoted by 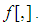 Wang and Liu developed in [9] a new modified Ostrowski’s method:
Wang and Liu developed in [9] a new modified Ostrowski’s method: 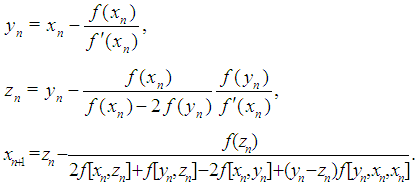 | (4) |
Another modifications of Ostrowski’s method were developed in [2, 5, 6]. The first two steps are the same as in (4) and the third step is different in these methods.All the above mentioned optimal eighth-order methods have the efficiency index  In this paper based on King’s method (2), we derive a new family of eighth-order methods for any
In this paper based on King’s method (2), we derive a new family of eighth-order methods for any  It has a form:
It has a form:  | (5) |
which includes the method (4) proposed in [9] as a particular case when 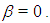 It requires, as in (3), (4) the evaluations of only three function and one first-order derivative per iteration. Therefore it has also efficiency index
It requires, as in (3), (4) the evaluations of only three function and one first-order derivative per iteration. Therefore it has also efficiency index 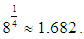
2. Construction of a Family of Iterative Methods and Convergence Analysis
We consider the following iterative methods 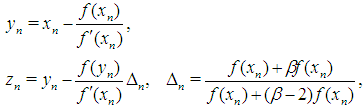 | (6) |
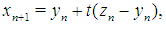 | (7) |
where 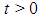 is a real parameter to be determined.Note that the two first steps in (6) and (7) is King’s iteration and the third step is a linear combination of the two approximations
is a real parameter to be determined.Note that the two first steps in (6) and (7) is King’s iteration and the third step is a linear combination of the two approximations  and
and 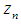 obtained by preceding steps. We call this iteration (6) and (7) as a modified King’s iterations.It is well known that the King’s method prescribed by the two first steps in (6) and (7) has a optimal fourth order convergence [4]. The third step in (6) and (7) can be considered as a accelerating procedure for King’s method.From (7) it clear that
obtained by preceding steps. We call this iteration (6) and (7) as a modified King’s iterations.It is well known that the King’s method prescribed by the two first steps in (6) and (7) has a optimal fourth order convergence [4]. The third step in (6) and (7) can be considered as a accelerating procedure for King’s method.From (7) it clear that 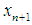 belongs to interval connecting
belongs to interval connecting 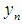 and
and 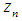 under condition
under condition 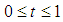 and does not belong to this interval when
and does not belong to this interval when 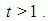 Our aim is to find optimal value
Our aim is to find optimal value 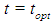 in (7) such that the new approximation
in (7) such that the new approximation 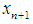 will be situated more close to
will be situated more close to 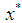 as compared with
as compared with 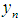 and
and 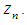 From this we deduce that
From this we deduce that 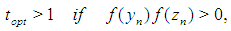 | (8) |
and 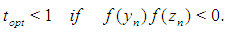 | (9) |
Now we proceed to analyse the convergence of iteration (6) and (7). For convenience, we rewrite 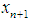 as
as 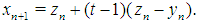 | (10) |
We use Taylor expansion of 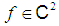 around
around 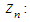
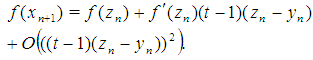 | (11) |
Now we approximate 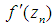 using already computed function values. This can be done by the method of undetermined coefficients, such that
using already computed function values. This can be done by the method of undetermined coefficients, such that 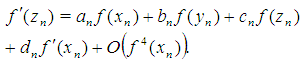 | (12) |
By using the Taylor expansions of 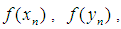
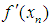 around
around 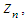 we obtain the following linear system of equations
we obtain the following linear system of equations  | (13) |
which has a unique solution: 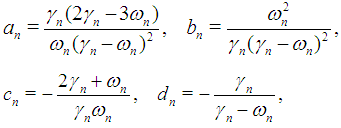 | (14) |
where 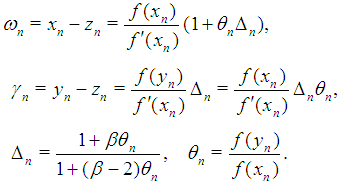 | (15) |
A simple calculations give us 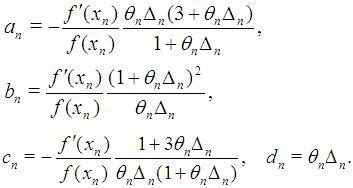 | (16) |
Substituting (16) into (12) we get 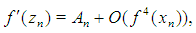 | (17) |
where 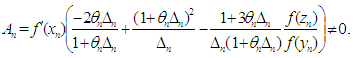 | (18) |
Substituting (17) into (11) we get 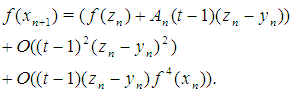 | (19) |
Now we are ready to state the following convergence theorem for the family of methods (6) and (7). Theorem 1 Assume that the function 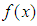 is sufficiently differentiable and
is sufficiently differentiable and 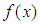 has a simple zero
has a simple zero 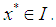 If the initial point
If the initial point 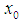 is sufficiently close to
is sufficiently close to 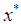 and the parameter
and the parameter 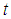 is chosen by
is chosen by 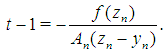 | (20) |
Then the method defined by (6) and (7) converges to 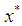 with eighth-order. Proof. The first term in brackets in (19) vanishes under choice (20). From (6) we see that
with eighth-order. Proof. The first term in brackets in (19) vanishes under choice (20). From (6) we see that 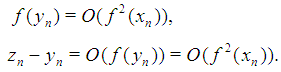 | (21) |
Since the King’s method has a fourth order of convergence, we also have  | (22) |
If we take (18) and (21), (22) into account, then from (20) we get 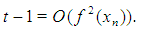 | (23) |
Using (21), (22) and (23) in (19) we arrive 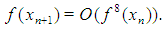 It means that there exists
It means that there exists  such that
such that 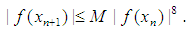 | (24) |
On the other hand, by mean-value theorem we have 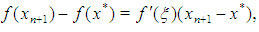 | (25) |
where 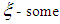 point lying between
point lying between 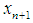 and
and 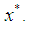 Since
Since 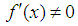 on the interval
on the interval 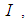 there exist the constants
there exist the constants 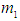 and
and 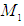 such that
such that 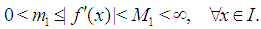 | (26) |
Then using (24) and (26) in (25) we obtain 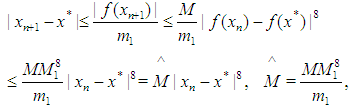 which completes the proof of Theorem 1. According to (10) and (20) the third step (7) reads as
which completes the proof of Theorem 1. According to (10) and (20) the third step (7) reads as 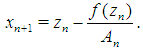 | (27) |
It is easy to show that 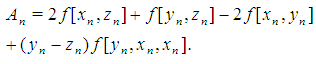 | (28) |
Then the proposed iterative methods (6) and (7) can be rewritten as (11).We call the value t given by (20), the optimal one.Using (6) and (18) in (20) we obtain 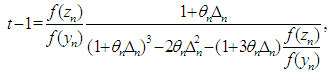 | (29) |
where 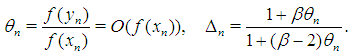 By virtue of (21) and (22) we have
By virtue of (21) and (22) we have 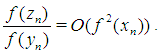 Then from (29) we have
Then from (29) we have 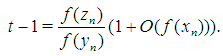 | (30) |
The factor 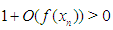 because of
because of 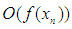 is small enough. Thus the inequalities (8) and (9) will be hold for the approximations
is small enough. Thus the inequalities (8) and (9) will be hold for the approximations 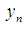 and
and 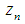 sufficiently close to
sufficiently close to 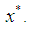
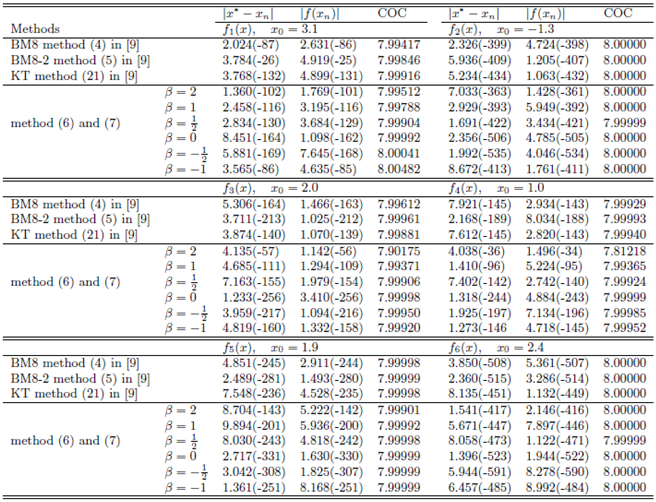
Table 1.
 |
| |
|
3. Numerical Experiments
We takes six examples from [9], 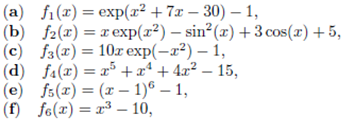 All numerical calculations were performed using Maple 18 system. To study the convergence of iterations, we compute the computational order of convergence (COC) of
All numerical calculations were performed using Maple 18 system. To study the convergence of iterations, we compute the computational order of convergence (COC) of  using the formulae
using the formulae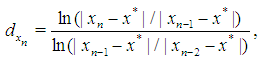 | (31) |
where 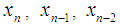 are three consecutive approximations of iterations.In this Table 1, we present the results of some numerical tests to compare the efficiencies of the methods. We employed, the BM8 method with
are three consecutive approximations of iterations.In this Table 1, we present the results of some numerical tests to compare the efficiencies of the methods. We employed, the BM8 method with 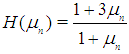 ((4) in [9]), the BM8-2 method with
((4) in [9]), the BM8-2 method with 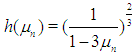 ((5) in [9]), the method (12) in [9], the KT method ((21) in [9]) and new method (6) and (7). In Table 1,
((5) in [9]), the method (12) in [9], the KT method ((21) in [9]) and new method (6) and (7). In Table 1, 
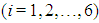 are the test functions,
are the test functions, 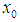 is the initial approximation.The factor
is the initial approximation.The factor 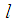 in the brackets denotes
in the brackets denotes 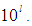 From tables we see that the COC perfectly coincides with the theoretical order and new method (6) and (7) is comparable with other optimal order methods.
From tables we see that the COC perfectly coincides with the theoretical order and new method (6) and (7) is comparable with other optimal order methods.
4. Conclusions
We propose a new family of eighth–order methods based on King’s methods. The high order of convergence is obtained by acceleration procedure. Numerical results clearly demonstrate the theoretical analysis (speed of convergence). Moreover, our acceleration procedure can also be applied to any iteration, for which will be devoted forth coming paper.
ACKNOWLEDGMENTS
The work was supported partially by the Foundation of Science and Technology of Mongolia under grant SST_007/2015.
References
| [1] | W. Bi, H. Ren and Q. Wu, Three-step iterative methods with eighth-order convergence for solving nonlinear equations, J. Comput. Appl. Math. 225 (2009) 105–112. |
| [2] | A. Cordero, J. R. Torregrosa and M. P. Vassileva, Three-step iterative methods with optimal eighth-order convergence, Numerical Algorithms, 54 (2011) 3189–3194. |
| [3] | A. Cordero, J. L. Hueso, E. Martinez and J. R. Torregrosa, New modifications of Potra-Ptak’s method with optimal fourth and eighth. |
| [4] | R. King, A family of fourth order methods for nonlinear equations, SIAM, Journal on Numerical Analysis, 10 (1973) 876–879. |
| [5] | T. Lotfi, S. Sharifi, M. Salimi and S. Siegmund, A new class of three-point methods with optimal convergence order eight and its dynamics, Numer. Algor. 68 (2015) 261–288. |
| [6] | J. R. Sharma and R. Sharma, A new family of modified Ostrowski’s methods with accelerated eighth-order convergence, Numer. Algor. 54 (2010) 445–458. |
| [7] | H. I. Siyyam, M. T. Shatnawi and I. A. Subaihi, A new one parameter family of iterative methods with eighth-order of convergence for nonlinear equations, Inter. Journal of Pure and Applied Mathematics, 84 (2013) 451–461. |
| [8] | R. Thukral and M. S. Petkovic, A family of the three-point methods of optimal order for solving nonlinear equations, J. Comput. Appl. Math. 233 (2010) 2278–2284. |
| [9] | L. Liu and X. Wang, Modified Ostrowski’s method with eighth-order convergence and high efficiency index, Appl. Math. Letters. 23 (2010) 549–554. |


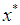 of a nonlinear equation
of a nonlinear equation 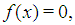
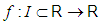 is a scalar function on the open interval
is a scalar function on the open interval 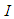 .The constructing of higher-order convergence methods has attracted a lot of attention from both theoretical as well as practical point of view, see for example [1-9] and references therein.King in [3] developed a one-parameter family of fourth-order methods, which is written as
.The constructing of higher-order convergence methods has attracted a lot of attention from both theoretical as well as practical point of view, see for example [1-9] and references therein.King in [3] developed a one-parameter family of fourth-order methods, which is written as 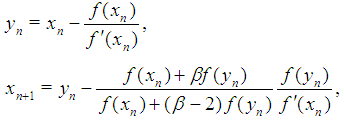
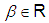 is a parameter. In particular, the famous Ostrowski’s method is a member of this family when
is a parameter. In particular, the famous Ostrowski’s method is a member of this family when 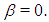 Recently, based on King’s or Ostrowski’s method, some optimal order iterative methods have been proposed and analyzed for solving nonlinear equations [1, 2, 5, 6, 8, 9]. In particular, Bi et al [1] presented a new family of eighth-order methods:
Recently, based on King’s or Ostrowski’s method, some optimal order iterative methods have been proposed and analyzed for solving nonlinear equations [1, 2, 5, 6, 8, 9]. In particular, Bi et al [1] presented a new family of eighth-order methods: 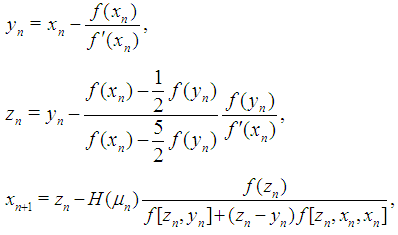
 and
and 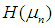 represents a real-valued function, satisfying the conditions
represents a real-valued function, satisfying the conditions 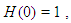
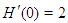 and
and 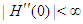 and divided differences are denoted by
and divided differences are denoted by 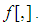 Wang and Liu developed in [9] a new modified Ostrowski’s method:
Wang and Liu developed in [9] a new modified Ostrowski’s method: 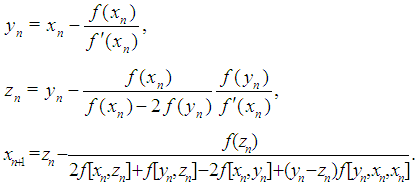
 In this paper based on King’s method (2), we derive a new family of eighth-order methods for any
In this paper based on King’s method (2), we derive a new family of eighth-order methods for any  It has a form:
It has a form: 
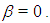 It requires, as in (3), (4) the evaluations of only three function and one first-order derivative per iteration. Therefore it has also efficiency index
It requires, as in (3), (4) the evaluations of only three function and one first-order derivative per iteration. Therefore it has also efficiency index 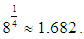
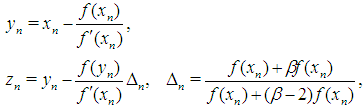
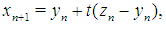
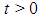 is a real parameter to be determined.Note that the two first steps in (6) and (7) is King’s iteration and the third step is a linear combination of the two approximations
is a real parameter to be determined.Note that the two first steps in (6) and (7) is King’s iteration and the third step is a linear combination of the two approximations  and
and 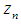 obtained by preceding steps. We call this iteration (6) and (7) as a modified King’s iterations.It is well known that the King’s method prescribed by the two first steps in (6) and (7) has a optimal fourth order convergence [4]. The third step in (6) and (7) can be considered as a accelerating procedure for King’s method.From (7) it clear that
obtained by preceding steps. We call this iteration (6) and (7) as a modified King’s iterations.It is well known that the King’s method prescribed by the two first steps in (6) and (7) has a optimal fourth order convergence [4]. The third step in (6) and (7) can be considered as a accelerating procedure for King’s method.From (7) it clear that 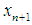 belongs to interval connecting
belongs to interval connecting 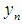 and
and 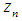 under condition
under condition 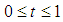 and does not belong to this interval when
and does not belong to this interval when 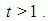 Our aim is to find optimal value
Our aim is to find optimal value 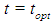 in (7) such that the new approximation
in (7) such that the new approximation 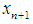 will be situated more close to
will be situated more close to 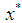 as compared with
as compared with 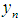 and
and 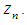 From this we deduce that
From this we deduce that 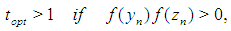
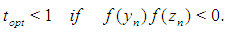
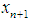 as
as 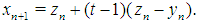
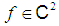 around
around 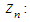
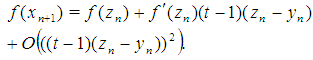
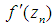 using already computed function values. This can be done by the method of undetermined coefficients, such that
using already computed function values. This can be done by the method of undetermined coefficients, such that 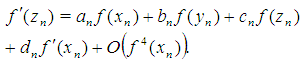
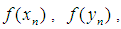
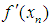 around
around 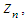 we obtain the following linear system of equations
we obtain the following linear system of equations 
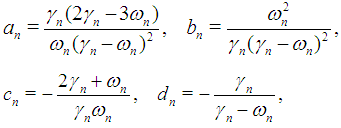
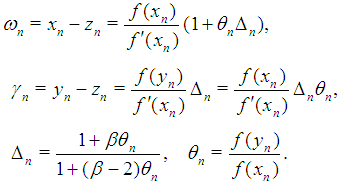
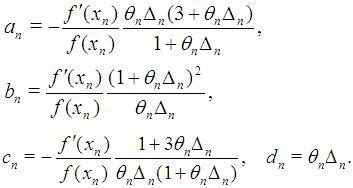
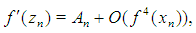
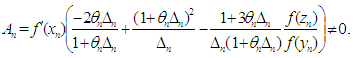
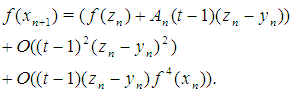
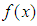 is sufficiently differentiable and
is sufficiently differentiable and 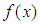 has a simple zero
has a simple zero 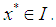 If the initial point
If the initial point 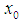 is sufficiently close to
is sufficiently close to 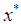 and the parameter
and the parameter 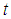 is chosen by
is chosen by 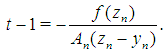
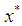 with eighth-order. Proof. The first term in brackets in (19) vanishes under choice (20). From (6) we see that
with eighth-order. Proof. The first term in brackets in (19) vanishes under choice (20). From (6) we see that 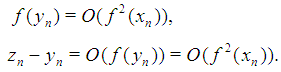

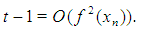
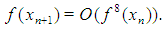 It means that there exists
It means that there exists  such that
such that 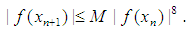
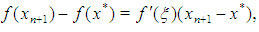
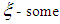 point lying between
point lying between 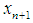 and
and 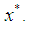 Since
Since 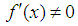 on the interval
on the interval 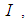 there exist the constants
there exist the constants 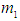 and
and 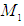 such that
such that 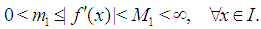
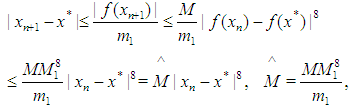 which completes the proof of Theorem 1. According to (10) and (20) the third step (7) reads as
which completes the proof of Theorem 1. According to (10) and (20) the third step (7) reads as 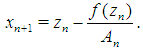
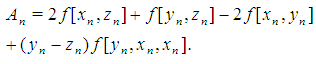
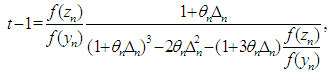
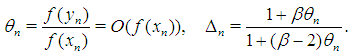 By virtue of (21) and (22) we have
By virtue of (21) and (22) we have 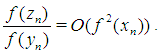 Then from (29) we have
Then from (29) we have 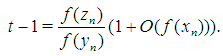
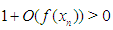 because of
because of 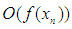 is small enough. Thus the inequalities (8) and (9) will be hold for the approximations
is small enough. Thus the inequalities (8) and (9) will be hold for the approximations 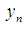 and
and 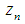 sufficiently close to
sufficiently close to 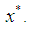
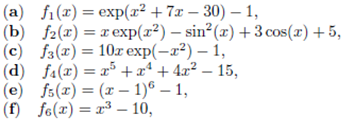 All numerical calculations were performed using Maple 18 system. To study the convergence of iterations, we compute the computational order of convergence (COC) of
All numerical calculations were performed using Maple 18 system. To study the convergence of iterations, we compute the computational order of convergence (COC) of  using the formulae
using the formulae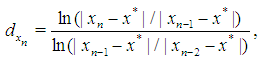
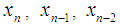 are three consecutive approximations of iterations.In this Table 1, we present the results of some numerical tests to compare the efficiencies of the methods. We employed, the BM8 method with
are three consecutive approximations of iterations.In this Table 1, we present the results of some numerical tests to compare the efficiencies of the methods. We employed, the BM8 method with 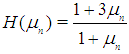 ((4) in [9]), the BM8-2 method with
((4) in [9]), the BM8-2 method with 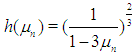 ((5) in [9]), the method (12) in [9], the KT method ((21) in [9]) and new method (6) and (7). In Table 1,
((5) in [9]), the method (12) in [9], the KT method ((21) in [9]) and new method (6) and (7). In Table 1, 
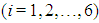 are the test functions,
are the test functions, 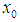 is the initial approximation.The factor
is the initial approximation.The factor 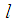 in the brackets denotes
in the brackets denotes 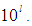 From tables we see that the COC perfectly coincides with the theoretical order and new method (6) and (7) is comparable with other optimal order methods.
From tables we see that the COC perfectly coincides with the theoretical order and new method (6) and (7) is comparable with other optimal order methods.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML