Usama H. Hegazy, Hatem F. Hamato
Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine
Correspondence to: Usama H. Hegazy, Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The dynamic behavior of a single degree of freedom nonlinear system under two different excitations, external and parametric excitations, are studied and the cases of primary and subharmonic resonances are considered separately. The approximate solutions are obtained using the method of multiple scales perturbation technique. The effects of the system parameters on the frequency- and force- response curves are investigated and compared with the results obtained from numerical simulations.
Keywords:
Nonlinearity effect, Primary resonance, Parametric resonance, Perturbation technique
Cite this paper: Usama H. Hegazy, Hatem F. Hamato, Dynamic Responses to Different Excitations of One Degree of Freedom System with Quadratic and Cubic Nonlinearities, American Journal of Computational and Applied Mathematics , Vol. 6 No. 4, 2016, pp. 165-176. doi: 10.5923/j.ajcam.20160604.03.
1. Introduction
The primary resonant optimal control for homoclinic bifurcations in single-degree-of-freedom nonlinear oscillators is studied. The response of uniform hinged-clamped beams and a uniform beam, respectively, to primary resonances of either the first or the second mode are investigated [2-4]. Moreover, the primary resonance of the first mode and a combination subharmonic resonance of the first two modes are considered to investigate the response of a uniform hinged-clamped beam [5]. The analysis of codimension-3 degenerate bifurcation for a simply supported quintic nonlinear beam with the focus on homoclinic and heteroclinic bifurcations are presented. It is found that multiple limit cycles may simultaneously exist for quintic nonlinearity [6]. The nonlinear behavior of a cantilever beam subjected to external and parametric excitations is studied. The cases of primary and subharmonic resonance are considered and the multiple scales method is used to obtain two first order ordinary differential equations. Effects of different parameters are investigated and the approximate solution is verified numerically [7]. The governing equations of a flexible cantilever Euler-Bernouli beam are obtained and solved numerically using the Rayleigh-Ritz method and automatic ordinary differential equation (ODE) solver. The perturbation method of multiple scales is utilized to obtain an approximate solution considering internal resonance case [8]. The nonlinear response of a forced single-degree-of-freedom weakly nonlinear oscillator under primary, superharmonic and subharmonic resonance cases is investigated. A nonlinear parametric feedback control is proposed to suppress the resonant vibrations of the oscillator and to eliminate the saddle-node bifurcations [9]. The harmonic resonance for one-degree-of-freedom system with quadratic, cubic and quartic nonlinearities under external and parametric excitations is investigated. The equations that describe the modulation of the amplitude and phase are determined using the method of multiple scales to the second order approximation. Numerical simulations are performed to verify analytical predictions [10]. The free and forced nonlinear flexural vibration of nonrotating thin circular ring with cubic nonlinear terms are examined. The trivial and nontrivial periodic responses of the system are derived using the multiple scales method under primary resonance and bifurcation of these solutions is studied. The analytical results are compared with those obtained from numerical integration [11]. The descritized equation of motion of a single-link flexible viscoelastic Cartesian manipulator with linear and nonlinear damping terms, forced and parametric excitations is obtained and investigated. Approximate solution is determined and the stability and bifurcation of the system are studied applying the method of multiple scales. The effect of material loss factor, mass ratio and amplitude of the excitation force on the frequency response curves are discussed [12]. The two-to-one resonance behavior of a free quadratically weakly nonlinear oscillator under a delayed feedback control is investigated. The normal form theory, centre manifold theorem and the multiple scales method are applied. It is found that a table two-mode solution and quasi-periodic solution may occur in the neighborhood of two-to-one resonant Hopf bifurcations. Numerical examples are given to illustrate the observed behavior [13].In this paper, the nonlinear dynamic behavior of a single-degree-of-freedom to different excitations is analyzed and studied under primary and principal parametric resonances. The method of multiple scales is applied to obtain the modulation equations of the amplitude and phase of the system. The stability of the periodic responses of the system is examined using the frequency response function and the phase-plane methods. Numerical integration is carried out to verify the obtained theoretical predictions.
2. Mathematical Analysis
The governing equation of motion to be studied and solved has the from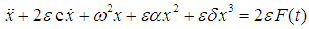 | (1) |
where x is the displacement, the dot indicates differentiation with respect to time t, for F(t) = f sin(Ωt) the force is called external force, and when F(t) = x f sin(Ωt) , it is called parametric excitation, ε is a small bookkeeping perturbation parameter, c is the damping coefficient, ω is the natural frequency, Ω is the forcing frequency, f is the forcing amplitude, α and δ are quadratic and cubic nonlinear coefficients, respectively.In this section the solution of the differential equation (1) is analyzed, applying the method of multiple scales. We assume that x is in the form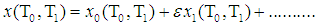 | (2) |
Where 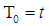 is the fast time scale and
is the fast time scale and 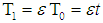 is the slow time scale. The time derivatives are expressed as
is the slow time scale. The time derivatives are expressed as 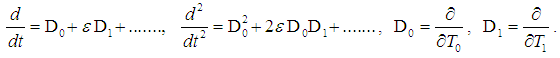 Thus, we have
Thus, we have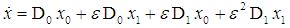 | (3) |
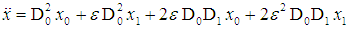 | (4) |
Substituting 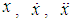 in equation (1) we obtain
in equation (1) we obtain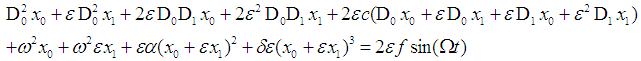 | (5) |
Expanding equation (5) gives,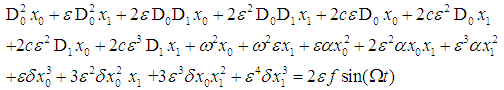 | (6) |
Considering the coefficients of 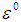 and
and 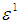 only, we get
only, we get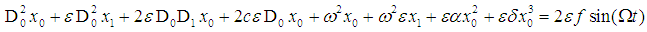 | (7) |
Now equating the coefficient of same powers of ε yields: 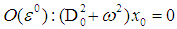 | (8) |
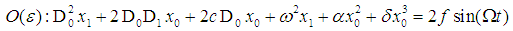 Or
Or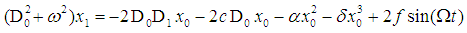 | (9) |
The general solution of (8) is given by 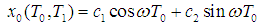 Using
Using 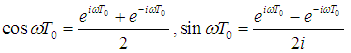
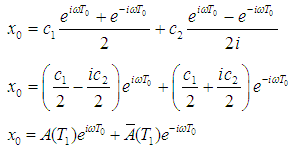 | (10) |
Now using equation (10) in equation (9), gives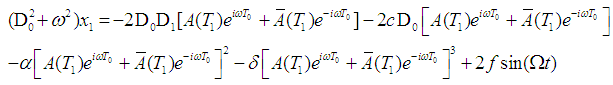 | (11) |
Simplifying equation (11) we obtain 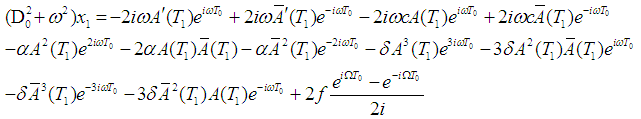 | (12) |
Or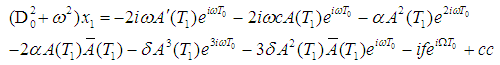 | (13) |
where cc is a complex conjugate for every preceding term. Rearranging equation (13), yield 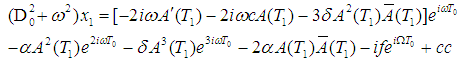 | (14) |
The particular solution of equation (14) is given by 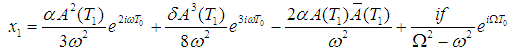 | (15) |
3. Stability Analysis
The cases of primary resonance and principal parametric resonance due to external and parametric forces, respectively, are considered and studied.
3.1. The primary Resonance Case Ω ≅ ω
The primary resonance case occurs when Ω is very close toω, which is expressed as 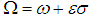 | (16) |
From equation (14) the secular terms, which result in unbounded solution, are eliminated and the solvability condition yield 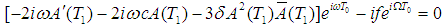 | (17) |
Using equation (16) into (17), T1= εT0, and Dividing by 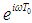 , we get
, we get 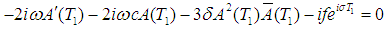 | (18) |
Using the following polar form expression in (18).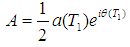 | (19) |
where 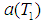 ,
, 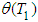 are the steady-state amplitude and phase of the motion, respectively. Then Separating imaginary and real parts of equation, we obtain
are the steady-state amplitude and phase of the motion, respectively. Then Separating imaginary and real parts of equation, we obtain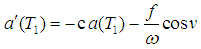 | (20) |
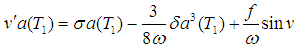 | (21) |
where 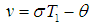 , and
, and  .The steady-state solutions correspond to constant
.The steady-state solutions correspond to constant 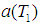 ,
, 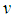 that is
that is 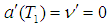 Thus equations (20) and (21) can be reduced to the following nonlinear algebraic equations
Thus equations (20) and (21) can be reduced to the following nonlinear algebraic equations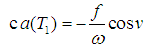 | (22) |
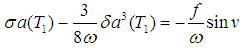 | (23) |
Squaring equations (22) and (23) then adding them, we obtain the following frequency response equation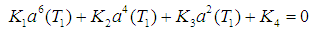 | (24) |
where 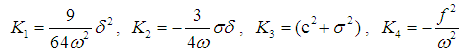
3.2. The Principal Parametric Resonance Case Ω ≅ 2ω
The principal parametric (subharmonic) resonance case occurs when the forcing frequency Ω is very close to twice the natural frequency ω, which is written as 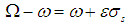 | (25) |
where σs is the principal parametric detuning parameter. In this case, following the same procedure as mentioned in section 3.1 with different detuning parameter, the following frequency response equation is obtained, which must also be satisfied so that the secular terms are eliminated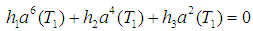 | (26) |
where 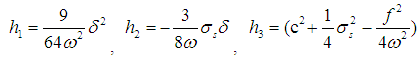 Now we study the problem of stability of linear (trivial) solutions for the two resonance cases.
Now we study the problem of stability of linear (trivial) solutions for the two resonance cases.
3.3. Trivial Solution
To determine the stability of the trivial solutions, one investigates the primary resonant solution of the linearized form of (18), that is 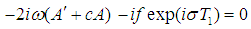 | (27) |
Introducing the following form into (27)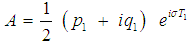 | (28) |
where p1, q1 are real, then separating real and imaginary parts, gives the following equations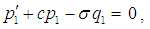 | (29) |
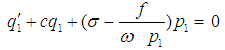 | (30) |
In a similar manner, one can obtain the following equations for the linearized form of the subharmonic resonant solution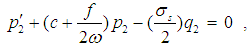 | (31) |
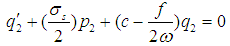 | (32) |
The above systems (29), (30) and (31), (32) are a first order autonomous ordinary differential equations, therefore the stability of a particular fixed point is determined by the eigenvalues of the Jacobian matrix of the right hand sides of (29), (30) and (31), (32). A given fixed point is stable if and only if the real parts of all eigenvalues are less than zero.
4. Numerical Results and Discussions
In this section, the solution of the frequency response equations (24), (26) and the nonlinear differential equation (1) are obtained numerically. The stability of the steady-state solution is investigated using the phase plane method and frequency response function and the numerical results are focused on the effect of different parameters.
4.1. Frequency- and Force-response curves
The results of solving (24) and (26) are shown in Figs. (1), (3) as the amplitude a against the detuning parameters σ, σs (frequency response curves) and in Figs. (2), (4) as the amplitude a against the forcing amplitude (force response curves).
4.1.1. Primary Response Solution
Considering Fig. 1a as a basic case to compare with, it can be seen from Figs. (1b-1c) that as the damping coefficient c and the natural frequency ω increase, the steady-state amplitude a decrease. Figure (1d) shows that the frequency response curves are bent to right when the nonlinear term δ is positive and to left when δ is negative leading to the appearance of jump phenomenon and indicating nonlinearity effect (either hardening or softening nonlinearity) of the nonlinear term δ. In Fig. (1e), the amplitude increases as the excitation force amplitude increases.The force response curves, where the steady-state amplitude a is plotted against the excitation force amplitude f and the detuning parameter σ is kept constant, are shown in Fig. (2) as the system parameters c, ω, δ, and σ are varied. It can be seen that magnitude of the amplitude is decreased and the curves are shifted downward when the parameters are increased. Figure (2e) shows that as the forcing amplitude f increases from zero to 3.0 and the detuning parameter σ is decreased, the amplitude of the response increases. For f > 3.0, the amplitude increases as σ is increased.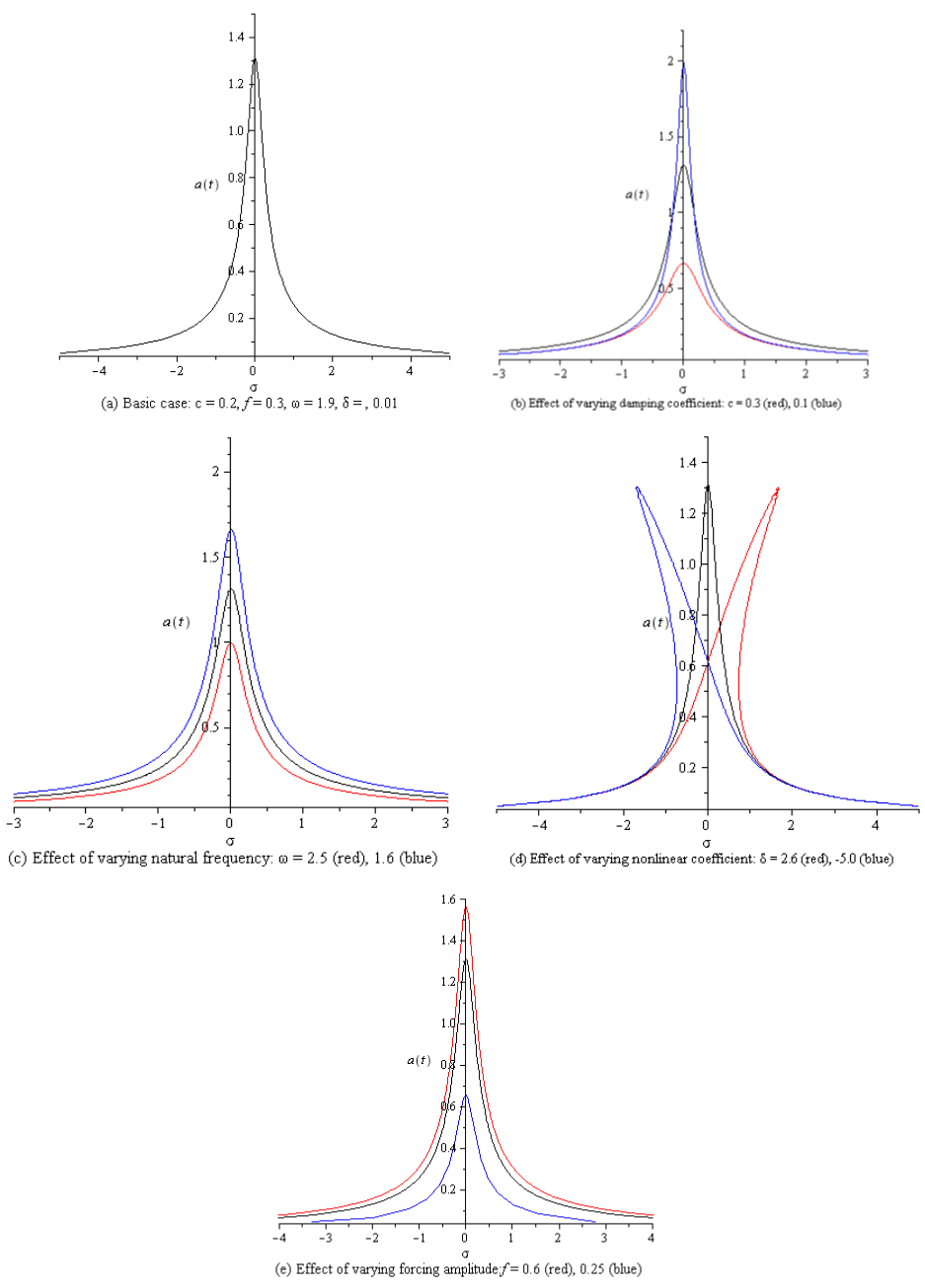 | Figure 1. Primary resonant frequency response curve under external force |
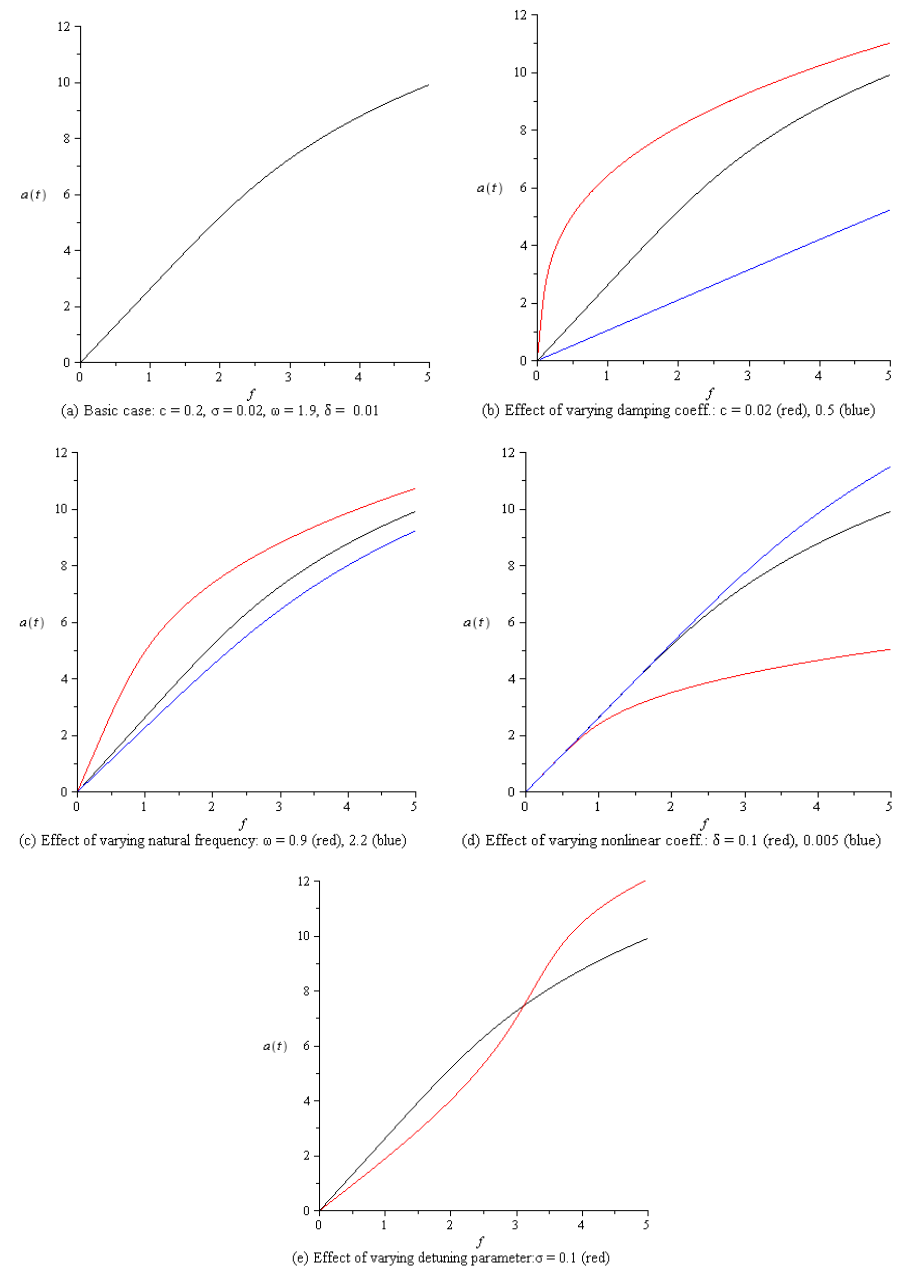 | Figure 2. Primary resonant force response curve under external force |
4.1.2. Principal Parametric Response Solution
Figs. (3a) shows the system under parametric excitation exhibits a softening nonlinearity response. In Fig. (3b-3c) when the damping coefficient c and the natural frequency ω decrease, the branches of the response curves diverge and the region of unstable solutions increase. The nonlinearity effect is shown in Fig. (3d), which also illustrate that an increase in the nonlinear term δ leads to a decrease in the steady-state amplitude a. As the parametric forcing amplitude is decreased, Fig. (3e), the branches of the response curves converge to each other, the region of unstable solutions and the steady-state amplitude decrease. The force response curves of the investigated system under parametric excitation are shown in Fig. (4) for different parameters values, where Fig. (4a) is considered as basic case for comparison. The force response curves in Fig. (4b) are shifted to right with decreasing amplitude as the damping coefficient c increase. Fig. (4c) indicates that the effect of varying the natural frequency ω is insignificant on both the resonant force response curves and the steady state amplitude. The steady state amplitude decreases as the cubic nonlinear coefficient δ increases. As the subharmonic detuning parameter σs increases in Fig. (4e), the force response curves are shifted to right, the steady state amplitude increases and the region of multivaludeness gets larger.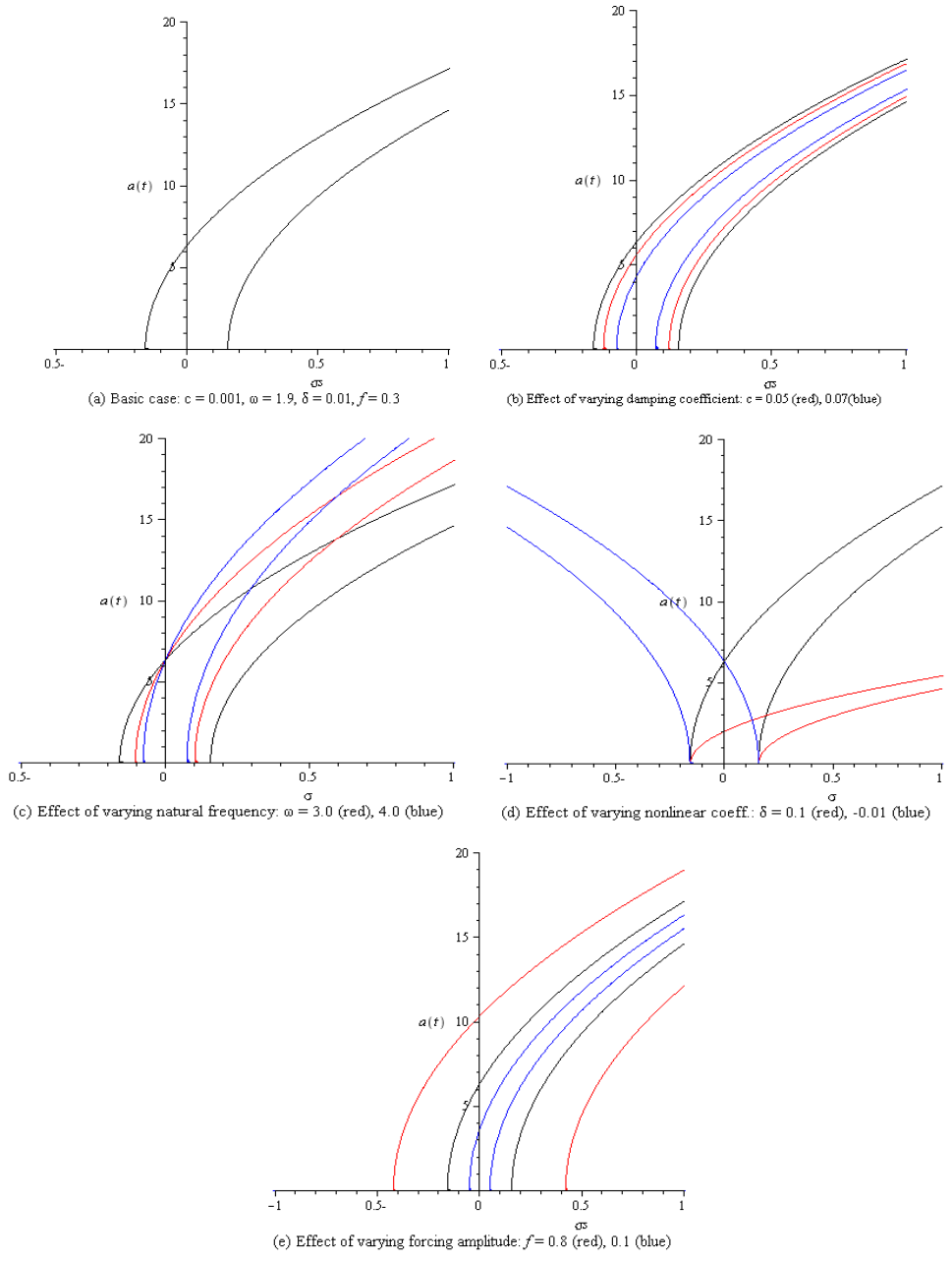 | Figure 3. Subharmonic resonant frequency response curve under parametric excitation |
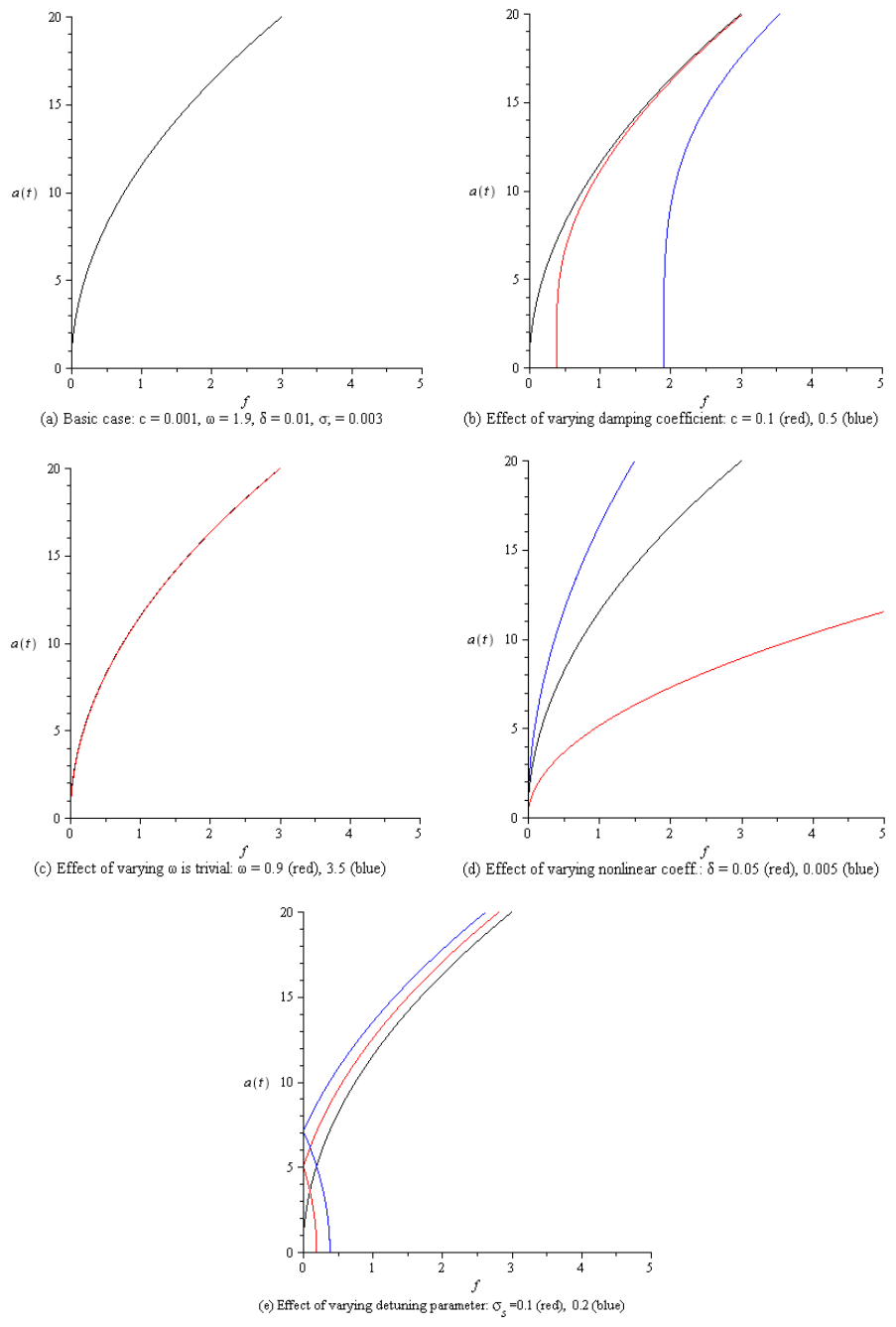 | Figure 4. Subharmonic resonant force response curve under parametric force |
4.2. Numerical Solution
In order to verify the analytic results, the equation of motion (1) is numerically integrated using a fourth order Runge-Kutta algorithm. Figures (5a) and (6a) show the behavior of nonresonant system under external excitation with zero initial conditions, and under parametric excitation with x(0) = 0.3 and zero initial velocity, respectively. The time response of the system under the primary and subharmonic resonant conditions, Fig. (5b) and (6b), respectively, illustrates that the steady-state amplitude increased to about 270% and 2565%, respectively. Moreover, the time response of the system under subharmonic resonance condition becomes strongly modulated.It can be seen from Figs. 7(a) and (5b) that at the beginning, as the initial conditions are increased, the transient time is increased but the steady-state amplitude is decreased. Whereas, Figs.(7b) and (6b) indicates that the transient time is decreased as initial conditions increase and the amplitude remains unchanged. This means that the system depends on initial conditions, and responses in a different manner as the kind of excitation force is varied, which is a characteristic of a nonlinear system.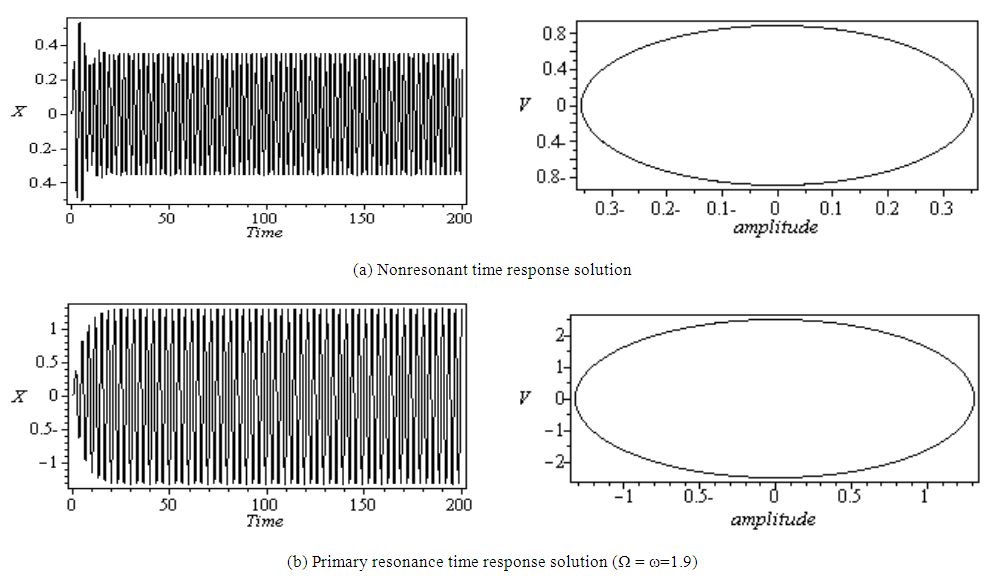 | Figure 5. Numerical solution of equation (1) to external force: c =0 .2, f = 0.5, ω = 1.9, Ω = 2.5, δ = 0.01, α = 0.04, and zero initial conditions |
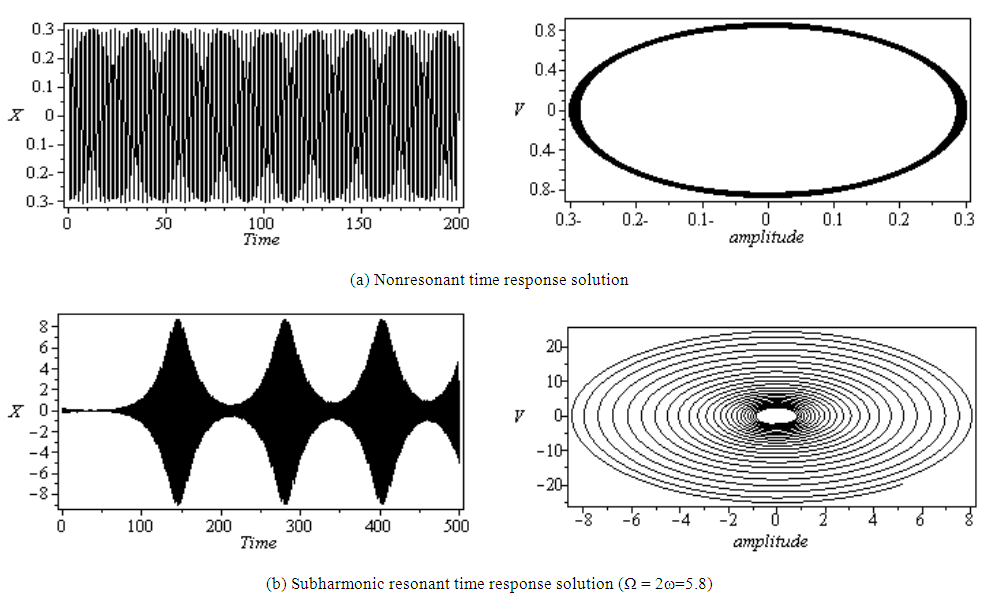 | Figure 6. Numerical solution of equation (1) to Parametric force: c =0 .001, f = 0.3, ω = 2.9, Ω = 3.5, δ = 0.01, α = 0.04, and initial condition x(0)=0.3 |
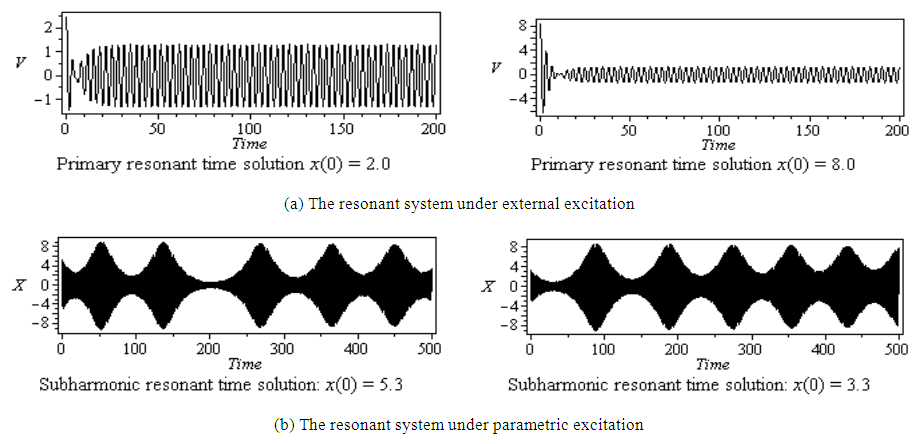 | Figure 7. Effect of initial conditions to the system under different excitations |
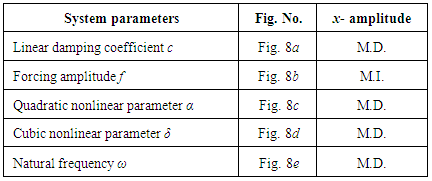
Figure (8) shows the effect of the system parameters on the primary and subharmonic resonant responses of the amplitude, which is summarized in the table 1.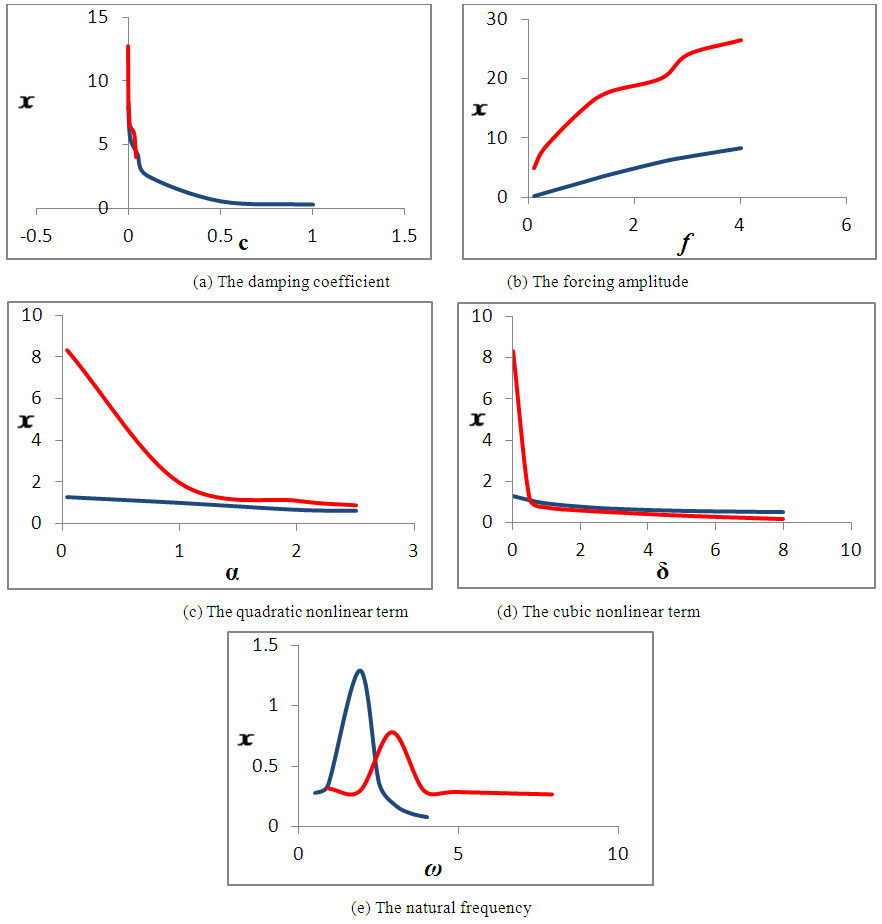 | Figure 8. Numerical solution of the system (1) under various values of the system parameters at primary resonance (blue) and subharmonic resonance (red). (x-axis: system parameter, y-axis: x-amplitude) |
Table 1. Effects of the system parameters
 |
| |
|
M.I. denotes that the amplitude is monotonic increasing function in the parameter. M.D. denotes that the amplitude is monotonic decreasing function in the parameter. Both effects of parameters in the response results, Figs. (1) – (4) and the numerical solution results, Fig. 8, are in a good agreement.
5. Conclusions
The present work examines primary resonance and principal parametric resonance, separately, for a nonlinear dynamical system subjected to external excitation and parametric excitation, respectively, using perturbation method up to and including the second order approximation. The frequency response equation is numerically solved to obtain the steady-state solution, and the stability of the resonant solutions is determined by the eigenvalues of the corresponding Jacobian matrix. The behavior of the system is studied applying Rung-Kutta fourth order method. The numerical solution is obtained at non-resonant case, primary resonance and principal parametric resonance cases under different initial conditions. The effect of different parameters on the system behavior and its stability are also investigated. Analytical results reveal that:1. For both types of forces, it is found that the frequency response curves consist of two branches. These curves are bent to right or left for some curves due to the nonlinearity effect (hardening or softening). This leads to multivalued solutions and hence to a jump phenomenon occurrence, which are typical characteristics of the behavior of nonlinear dynamical system.2. The steady-state amplitudes x of the system is monotonic increasing function in the forcing amplitude f.3. The steady-state amplitude x of the system is a monotonic decreasing function in the linear damping coefficient c and the cubic nonlinear parameter δ.4. The primary frequency- and force- response curves indicate that the steady-state amplitude x of the system is a monotonic decreasing function in the natural frequency ω. 5. The subharmonic response curves show that as ω is increased, the frequency- response curves are bent to left and the region of unstable solution is decreased. For the force-response curves, the variation of ω has insignificant effect.6. As the primary detuning parameter σ increases, the steady-state amplitude x of the system decreases when the external forcing amplitude f lies in the range [0, 3.0]. But when f > 3.0, x increases as σ continue to increase. In the subharmonic force-response curves, the steady-state amplitude x of the system is a monotonic decreasing function in detuning parameter σs for all values of the parametric forcing amplitude.Results of numerical integration indicate that:1. Each type of the applied forces produces various resonance cases and behavior. The resonance case with maximum peak of amplitudes is considered as the worst resonance case. Numerical results show that the worst resonance case under:a. harmonic forces occurs at the primary resonance case, at which the frequency of the excitation is close to the natural frequency of the system.b. parametric forces occurs at the subharmonic resonance case at which the frequency of the excitation is twice that of the natural frequency of the system and the behavior is strongly modulated, which is different from that produced by the harmonic forces.2. The system is sensitive to initial conditions and the system behavior is totally different in case of harmonic excitation from that of parametric excitation.3. The steady-state amplitude x of the system increases as both kinds of the forcing amplitudes increase. While x is inversely proportional to the linear damping coefficient c, the quadratic nonlinear parameter α and the cubic nonlinear parameter δ.
References
| [1] | Cao H., 2005. Primary resonant optimal control for homoclinic bifurcations in single-degree-of-freedom nonlinear oscillators. Chaos, Sol. Fract. 24, 1387–1398. |
| [2] | Nayfeh A.H., Mook D.T., Sridhar S., 1974. Nonlinear analysis of the forced response of structural elements. J. Acoust. Soc. Amer. 55, 281–291. |
| [3] | Sridhar S., Nayfeh A.H., Mook D.T., 1975. Nonlinear resonances in a class of multi-degree-of freedom systems. J. Acoust. Soc. Amer. 58, 113–123. |
| [4] | Chen S.H., Cheung Y.K., Lau S.L. 1989. On the internal resonances of multi-degree-of- freedom systems with cubic nonlinearities. J. Sound. Vib. 128, 13–24. |
| [5] | Lau S.L., Cheung Y.K., Chen S.H., 1989. An alternative perturbation procedure of scales for nonlinear dynamics system. ASME J. Appl. Mech. 56, 667–675. |
| [6] | Zhang W., Wang F-X., Zu J.W., 2005. Local bifurcations and codiension-3 degenerate bifurcations of a quintic nonlinear beam under parametric excitation. Chaos, Sol. Fract. 24, 977–998. |
| [7] | M. Eissa and Y.A. Amer, 2004. Vibration control of a cantilever beam subject to both external and parametric excitation. Appl. Math. Comput. 152, 611-619. |
| [8] | S. A. Siddiqui and M. Golnaraghi, 1998. Dynamics of a flexible cantilever beam carrying a moving mass. Nonlinear Dyn. 15, 137-154. |
| [9] | A. Y. T. Leung, J. C. Ji and G. Chen, 2004. Resonance control for a forced single-degree-of-freedom nonlinear system. Int. J Bifurcation and Chaos. 14(4), 1423-1429. |
| [10] | A. F. El-Bassiouny and M. Eissa, 2003. Dynamics of a single-degree-of-freedom structure with quadratic, cubic and quartic non-linearities to a harmonic resonance. Appl. Math. Comput. 139, 1-21. |
| [11] | M. Rougui, A. Karmni and M. Belhaq, 2008. Nonlinear flexural vibration of a circular ring. A single mode approach. Chaos Solitons Fractals. 37, 1143-1152. |
| [12] | B. Pratiher and S. K. Dwivedy, 2008. Non-linear vibration of a single link viscoelastic Cartesian manipulator. Inter. J. Non-linear Mech. 43, 683-696. |
| [13] | J. C. Ji, X. Y. Li, Z. Luo and N. Zhang, 2012. Two-to-one resonant Hopf bifurcations in a quadratically nonlinear oscillator involving time delay. Int. J Bifurcation and Chaos. 22(3), 1250060 (14 pages). |


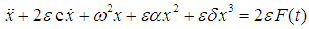
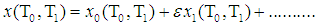
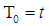 is the fast time scale and
is the fast time scale and 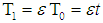 is the slow time scale. The time derivatives are expressed as
is the slow time scale. The time derivatives are expressed as 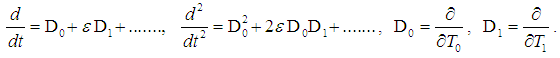 Thus, we have
Thus, we have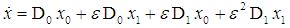
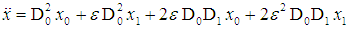
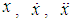 in equation (1) we obtain
in equation (1) we obtain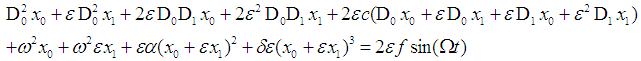
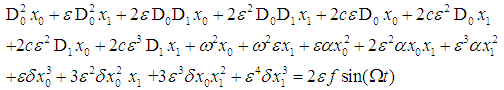
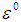 and
and 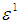 only, we get
only, we get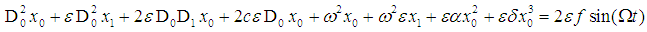
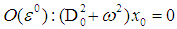
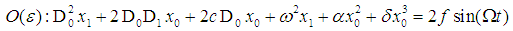 Or
Or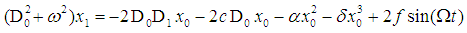
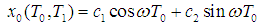 Using
Using 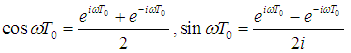
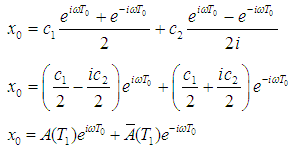
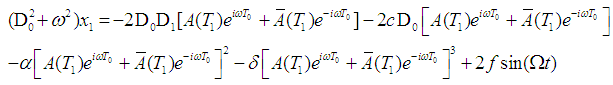
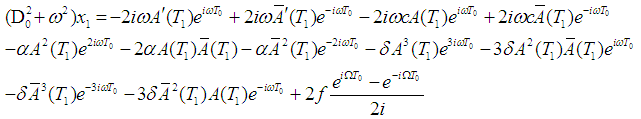
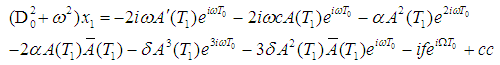
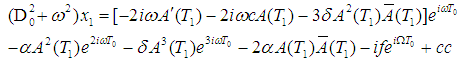
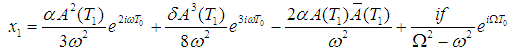
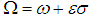
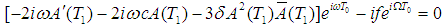
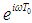 , we get
, we get 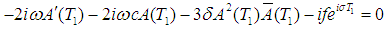
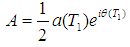
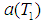 ,
,  are the steady-state amplitude and phase of the motion, respectively. Then Separating imaginary and real parts of equation, we obtain
are the steady-state amplitude and phase of the motion, respectively. Then Separating imaginary and real parts of equation, we obtain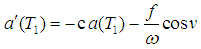
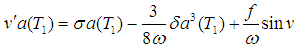
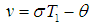 , and
, and  .The steady-state solutions correspond to constant
.The steady-state solutions correspond to constant 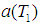 ,
, 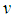 that is
that is 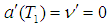 Thus equations (20) and (21) can be reduced to the following nonlinear algebraic equations
Thus equations (20) and (21) can be reduced to the following nonlinear algebraic equations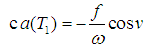
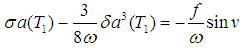
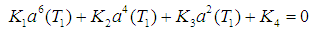
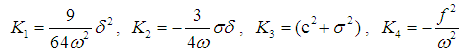
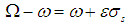
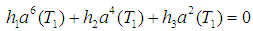
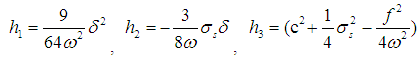 Now we study the problem of stability of linear (trivial) solutions for the two resonance cases.
Now we study the problem of stability of linear (trivial) solutions for the two resonance cases. 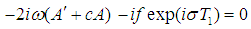
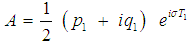
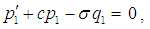
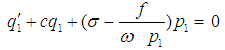
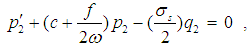
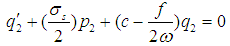







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
