Afrah Mohammad Ibraheem
Dep. of Mathematics, College of Education, Al-Mustansiriyah University, Baghdad, Iraq
Correspondence to: Afrah Mohammad Ibraheem, Dep. of Mathematics, College of Education, Al-Mustansiriyah University, Baghdad, Iraq.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Let R be a prime ring and d be a reverse derivation on R. If f is a generalized reverse derivation on R such that f is commuting and centralizing on a right ideal I of R, then R is a commutative.
Keywords:
Prime rings, Right ideals, Reverse derivations, Generalized reverse derivations, Centralizing and Commuting generalized reverse derivations
Cite this paper: Afrah Mohammad Ibraheem, Right Ideals and Generalized Reverse Derivations on Prime Rings, American Journal of Computational and Applied Mathematics , Vol. 6 No. 4, 2016, pp. 162-164. doi: 10.5923/j.ajcam.20160604.02.
1. Introduction
Let R be a ring with center Z. R is said to be prime if aRb = 0 implies that either a = 0 or b = 0. A mapping f is said to be commuting on a right ideal I of R if[x, f(x)] = 0 for all x ∈ I and f is said to be centralizing if [x, f(x)] ∈ Z (R) for all x ∈ I. An additive mapping d: R →R is called a derivation if d (xy) = d (x) y + xd (y) for all x, y ∈ R, and d is called a reverse derivation if d (xy) =d(y)x+ yd(x) for allx, y ∈ R. The notion of reverse derivation has been introduced by Bresar and Vukman [3], and the reverse derivations on semi prime rings have been studied by Samman and Alyamani [6]. An additive mapping f: R →R is said to be a generalized derivation on R if f (xy) = f (x) y + xd (y) for all x, y ∈ R, where d is a derivation on R, and f is said to be a generalized reverse derivation on R if f (xy)= f (y) x + yd (x) for all x, y ∈ R, where d is a reverse derivation on R. A. Aboubakr and S. Gonzalez [1] studied the relationship between generalized reverse derivation and generalized derivation on an ideal in semi prime rings, and in [4] the authors proved that in case R is a prime ring with a non-zero right reverse derivation d and U is the left ideal of R then R is commutative.In this paper we prove that a prime ring R is commutative if f is a generalized reverse derivation on R with a non zero derivation d on R such that f is centralizing and commuting on a right ideal I of R.
2. Preliminaries
Throughout, R will represent a prime ring with center Z. Let [x, y] = x y - y x with the important identity [x, yz] = y[x, z] + [x, y] z, and [xy, z] = [x, z] y + x[y, z], for all x, y, z ∈ R.In order to prove the main results, we being with following preliminary results. Remark (2.1) [2]: Let R be a prime ring. For a nonzero element a ∈ Z (R), if ab ∈ Z(R), then b ∈ Z (R).Lemma (2.2): Let R be a prime ring, and d be a reverse derivation on R. For an element a ∈ R, if a d(r) = 0 for all r ∈ R, then either a = 0 or d = 0.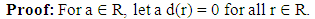 | (1) |
Replace r by sr in (1), we have a d (sr) = 0, then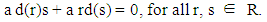 | (2) |
By used (1) in (2), we have a r d(s) = 0 for all r, s ∈ R.If d(s) ≠ 0 for some s ∈ R, then a = 0 by definition of prime ring. Hence proved. Lemma (2.3): Let I be a nonzero right ideal of a prime ring R. If R has a zero reverse derivation d on I, then d is also zero reverse derivation on R.Proof: Let I ≠ {0} is a right ideal of R. 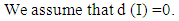 | (3) |
Since IR ⊆ R we have: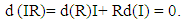 | (4) |
By substitute (3) in (4), we have d(R) I= {0}. Since I ≠ {0}, then by lemma (2.2), d(R) = 0.Lemma (2.4) [5]: Let R be a prime ring and I a non zero right ideal of R. If I is commutative, then R is also commutative.
3. Main Results
Theorem (3.1): Let R be a prime ring, and I be a non zero right ideal of R. If d is a non zero reverse derivation on R, such that d is a centralizing on I, then R is commutative.Proof: Let d be a centralizing on I, then we have 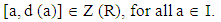 | (5) |
Replacing a by a2 in (5), we get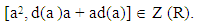 | (6) |
By add and subtract a d(a) in (6), we get[a2, 2ad(a) – [a, d(a)]] ∈ Z (R), for all a ∈ I. That’s equal to 2 [a2, ad(a)] = 4 a2 [a , d(a)] ∈ Z (R). Thus, 4 [a2 [a , d(a)], d(a)] = 0, for all a ∈ I.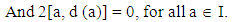 | (7) |
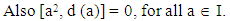 | (8) |
Now, linearizing both (5) and (7), we get[a, d (b)] + [b, d (a)] ∈ Z (R), and 2 [a, d(b)] + [b, d(a)] = 0, for all a, b ∈ I.By combining these results with (7), we can show that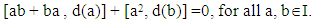 | (9) |
Replacing b by ba in (9), and using (8) and (9), we get[ab + ba, d(a)] a - a [ab + ba, d(a)] + d(a) [a2, b] = 0, for all a, b ∈ I. Then, we get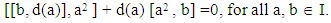 | (10) |
Replacing [b, d(a)] by a2 in (10), we get 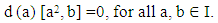 | (11) |
Replacing d(a) by d(a) r in (11), we getd (a) r [a2, b] =0, for all a, b ∈ I and r ∈ R.Since R is a prime, we have d(a) = 0 or [a2, b] = 0.If d(a)= 0 for all a ∈ I then by lemma (2.2), d(R)= 0 this is a contradiction. So [a2, b] = 0, for all a, b ∈ I, that’s mean I is commutative and hence by lemma (2.4), R is commutative.Theorem (3.2): Let R be a prime ring, and I be a right ideal of R. If f is a generalized reverse derivation on R with a reverse derivation d on R, such that f is centralizing on I, then for all a ∈ I∪Z (R), f (a) ∈ Z(R).Proof: Since f is centralizing on I, we have 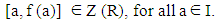 | (12) |
By linearizing (12) for all a, b ∈ I, we have 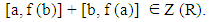 | (13) |
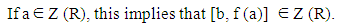 | (14) |
Replacing b by b f(a) in (14), we get [b, f (a)] f(a) ∈ Z (R), for all a, b ∈ I.If [b, f (a)] = 0, then f (a) ∈ CR (I), the centralizer of I in R, and hence f(a) ∈ Z (R). On the other hand if [b, f (a)] ≠ 0, then by remark (2.1), we get f (a) ∈ Z (R).Theorem (3.3): Let I be a nonzero right ideal of a prime ring R, and f is a generalized reverse derivation on R with a non zero reverse derivation d on R. If f is commuting on I, then R is commutative. Proof: Let f is commuting on I, then for all a ∈ I,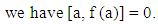 | (15) |
Replacing a by a+b in (15), we get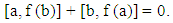 | (16) |
Substituting b = ba in (16), and using (15), we get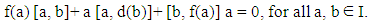 | (17) |
Replacing a by b in (17) and using (15), we get 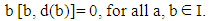 | (18) |
Now we substituting d(b)= d(b) r in (17), and using (18), we get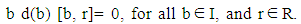 | (19) |
Replacing r by rs in (19), and using (19), we getb d(b) r [b, s]= 0, for all b ∈ I, and r, s ∈ R.Since R is a prime ring, and b d(b) ≠ 0, then [b, s] = 0, for all b ∈ I, and s ∈ R. Therefore b ∈ Z(R) and so I ⊆ Z(R), which implies that I is commutative and by lemma (2.4), R is commutative.Theorem (3.4): Let R be a prime ring, and I be a right ideal of R such that I∩Z(R) ≠ 0. Let f be generalized reverse derivations on R with a non zero reverse derivation d on R. If f is commuting on I, then R is commutative.Proof: Let we take Z(R) ≠ 0, since f is commuting on I then the proof is complete.Now, by equation (13), we have [a, f (b)] + [b, f (a)] ∈ Z(R), for all a, b ∈ I.If we replacing b by ar, where 0≠ r ∈ Z (R), we get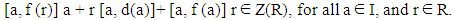 | (20) |
By using lemma (2.2) in (20) we have f(r) ∈ Z(R), and since f is centralizing on I, 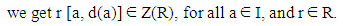 | (21) |
By using remark (2.1) in (21), we get [a, d(a)] ∈ Z(R), for all a ∈ I. And hence by theorem (3.1), R is commutative.
References
| [1] | A. Aboubakr and S. Gonzalez, Generalized reverse derivation on semi prime rings, Siberian mathematical journal, Vol.56, No.2, (2015), 199-205. |
| [2] | A. Ali and T. Shah, Centralizing and commuting generalized derivation on prime rings, Matematiqki Vesnik, 60 (2008), 1–2. |
| [3] | M. Bresar and J. Vukman, On some additive mappings in rings with involution, A equations math., 38 (1989), 178-185. |
| [4] | Jaya, Subba Reddy C. and Hemavathi K., Right reverse derivations on prime rings, International Journal of Research in Engineering & Technology, 2 (3), (2014), 141-144. |
| [5] | J. H. Mayne, Centralizing mappings of prime rings, Caned. Math. Bull., 27 (1), (1984), 122–126. |
| [6] | M. Samman, N. Alyamani, Derivations and reverse derivations in semi prime rings, International Mathematical Forum, 2 (39), (2007), 1895-1902. |



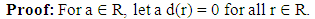
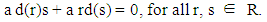
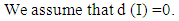
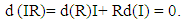
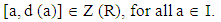
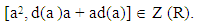
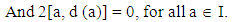
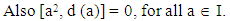
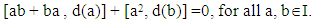
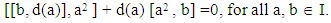
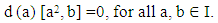
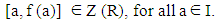
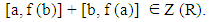
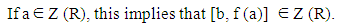
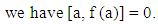
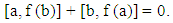
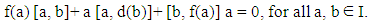
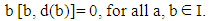
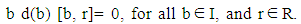
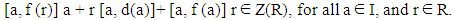
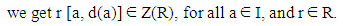
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML