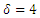-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(4): 149-161
doi:10.5923/j.ajcam.20160604.01

MHD Boundary Layer Flow Past an Inclined Plate with Viscous Dissipation
Ayine Azure Daniel, Yakubu Ibrahim Seini
Faculty of Mathematical Sciences, University for Development Studies, Tamale, Ghana
Correspondence to: Ayine Azure Daniel, Faculty of Mathematical Sciences, University for Development Studies, Tamale, Ghana.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper investigates the effect of inclination on the heat and mass transfer characteristics of a heated plate with viscous dissipation. An incompressible ferrofluid such as polyethylene oxide solution is made to uniformly flow over a heated plate and a transverse magnetic field applied to regulate the flow. The partial differential equations modeling the problem include the equation of mass conservation, the momentum equation, the energy equation and the concentration equation. The system of partial differential equations are transformed to a system of non linear ordinary differential equations by similarity transformation and solved with maple 16 by using the fourth order Runge Kutta method. The effects of variation of the angle of inclination α, the viscous dissipation parameter N, the chemical reaction parameter β and other relevant parameters have been displayed graphically, and corresponding numerical results tabulated and analyzed. It was evident that an increase in the angle of inclination resulted in significant increments in the velocity profile and skin friction coefficient in the boundary layer. It was also observed that increasing the angle of inclination from 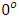 to
to 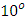 (the cooling angle) caused the plate’s temperature and concentration to decrease. However increasing the angle of inclination above
(the cooling angle) caused the plate’s temperature and concentration to decrease. However increasing the angle of inclination above 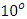 caused the temperature of the plate to increase. Also an increase in the viscous dissipation parameter caused the plate’s temperature to rise.
caused the temperature of the plate to increase. Also an increase in the viscous dissipation parameter caused the plate’s temperature to rise.
Keywords: Magneto-hydrodynamics (MHD), Ferrofluid, Inclination,Incompressible
Cite this paper: Ayine Azure Daniel, Yakubu Ibrahim Seini, MHD Boundary Layer Flow Past an Inclined Plate with Viscous Dissipation, American Journal of Computational and Applied Mathematics , Vol. 6 No. 4, 2016, pp. 149-161. doi: 10.5923/j.ajcam.20160604.01.
Article Outline
1. Introduction
- Regulation of the cooling process in manufacturing processes determines the quality of a desired product. It is therefore important to investigate techniques that have the potential of meeting this goal. Heat and mass transfer in magneto-hydrodynamic (MHD) boundary layer shows greater prospects of achieving this goal. Conventional base fluids such as water, air and oil have been known and used for cooling mechanical systems in industrial processes over many centuries. In recent times, the concept of boundary layer has become important due to its numerous applications in engineering innovations and industrial processes. An important application of the boundary layer theory is the determination of friction drag on bodies in a flow. Prandtl [24] introduced the boundary layer theory to study the flow structure of viscous fluids near solid boundaries. The early contribution in the field of fluid dynamics include that of Blasius [7] who solved the famous boundary layer equation for a flat moving plate problem and found a power series solution of the model. Skan and Falkner [29] generalized the Blaius problem by considering the boundary layer flow over a wedge inclined at a certain angle. A numerical solution of the classical Blasius problem was presented by Cortell [9]. Sakiadis [26] investigated the boundary layer flow over a continuously moving rigid surface with constant speed whilst Cortell [8] provided numerical solution of Sakiadis flow by including the radiation effects on the boundary layer. Crane [10] was the first to investigate the boundary layer flow due to a stretching surface and found exact solutions of the boundary layer equations. The boundary layer flow characteristics of a fluid in a porous media have been studied extensively because of its many engineering applications such as in the design of heat exchangers, catalytic reactors and other cooling devices. Numerous studies regarding heat and mass transfers in fluids on different orientations have been conducted. The effect of transpiration (suction or blowing) on ordinary fluid flow and heat transfer as well as skin friction coefficients for the steady, laminar and free convection boundary layer flow generated above a heated horizontal surface, has been studied extensively by Hossain and Mojumder [12]. Ibrahim and Makinde [14] conducted a theoretical study of the steady MHD boundary layer flow past a low-heat-resistant sheet moving vertically downwards, and observed that the buoyancy force parameter increases the velocity of the fluid and reduces the temperature due to convective cooling. Heat and mass transfer characteristics of natural convective flow of a chemically reacting Newtonian fluid along vertical and inclined plate in the presence of diffusion-thermo (Dufour) and thermal-diffusion (Soret) effects, was studied by Beg et al. [6]. The presence of chemical reaction and non-uniform heat source over an unsteady stretching surface was investigated by Seini [27]. He observed that the heat and mass transfer rates as well as the skin friction coefficient depended on the unsteadiness parameter, the space-dependent and the temperature- dependent parameters for heat source/sink. Heat and mass transfer in a boundary layer flow with thermal radiation past a moving vertical porous plate was examined by Makinde [18]. Reddy et al. [25] also analyzed the steady two-dimensional MHD free convection flow of viscous dissipating fluid past a semi-infinite moving vertical plate in a porous medium with Soret and Dufour effects. Mansour et al. [20] analytically studied the MHD flow of a micro polar fluid due to heat and mass transfer through a porous medium bounded by an infinite vertical porous plate in the presence of a transverse magnetic field in slip-flow regime. Similarly, the transient free convective flow of a viscous incompressible fluid over an infinite vertical porous plate embedded in highly porous medium of time dependent permeability under periodic suction, has been studied by Ahmed [3]. There are many transfer processes governed by the combined action of buoyancy forces due to both thermal and mass diffusion in the presence of chemical reaction. It has many applications in nuclear reactor technology, combustion, solar collectors, drying, dehydration, polymer production and in the operations of chemical and food processing plants. The effects of chemical reaction on a moving isothermal vertical surface with suction have been studied by Muthucumaraswamy [22]. Kandasamy [16] considered the chemical reaction and thermal stratification effects over a vertical stretching surface. Application of chemical reaction to a micropolar flow over an isothermal vertical cone has been studied by Abdou [1]. Ibrahim et al [13] studied the chemical reaction and absorption effects on the unsteady MHD flow past a semi-infinite vertical permeable moving plate with heat source and suction. Muthucumaraswamy [23] investigated the mass transfer effect on isothermal vertical oscillating plate in the presence of chemical reaction. The effect of chemical reaction on free convection flow through a porous medium bounded by a vertical surface was reported by Das [11]. Ibrahim and Makinde [15] studied the chemical reaction effect on MHD boundary layer flow of heat and mass transfer over a moving vertical plate with suction. Senapati [28] noticed that the mass concentration decreases with increasing reaction rate parameter. An Approximate analytic solution for MHD flow of non-Newtonian fluid over a vertical stretching sheet was obtained by Azeem and Ramzan [4]. They observed that the velocity profile decreased with an increased magnetic parameter and the temperature field decreased when the prandtl number was increased. Masood et al. [21] investigated an MHD Falkner-Skan flow with mixed convection and convective boundary condition and established that the temperature of the fluid significantly increased when the Biot number was increased. A note on convective heat transfer of an MHD Jeffrey fluid over a stretching sheet by Ahmed J. et al. [2], revealed a remarkable decrease in the value of the Nusselt number when the magnetic parameter was increased. MHD flow of a non-Newtonian power law fluid over a vertical stretching sheet with convective boundary condition was conducted by Azeem and Ramzan [5]. They observed an increase in temperature of the fluid and the thermal boundary layer when the magnetic parameter was increased. Many industrial processes involve the transfer of heat by means of flowing fluids. Ferrofluid flows over inclined surfaces possess the potential of enhancing efficient heat transfer. This can be achieved by allowing a ferrofluid to flow over an inclined surface with a magnetic field applied transversely on the inclined surface to regulate the flow and the cooling process. This has not been investigated; hence the need for this research. This research is useful in the building of small heat transfer systems with lower capital cost and improved efficiency. The findings in this study can greatly benefit various industries such as the electronic, medical, food processing and manufacturing industries as well as nuclear reactor technology.
1.1. Nomenclature
- Ÿ
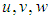 : Velocity components along the
: Velocity components along the 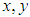 and
and 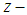 axis directions, respectivelyŸ
axis directions, respectivelyŸ 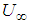 : Velocity of fluid far away from the plateŸ
: Velocity of fluid far away from the plateŸ 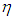 : Similarity variableŸ
: Similarity variableŸ 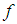 : Dimensionless velocityŸ
: Dimensionless velocityŸ 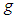 : Acceleration due to gravityŸ
: Acceleration due to gravityŸ 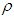 : Fluid densityŸ
: Fluid densityŸ 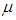 : Dynamic viscosityŸ
: Dynamic viscosityŸ 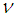 : Kinematic viscosityŸ
: Kinematic viscosityŸ 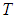 : TemperatureŸ
: TemperatureŸ 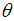 : Dimensionless TemperatureŸ
: Dimensionless TemperatureŸ 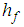 : Heat transfer coefficient Ÿ
: Heat transfer coefficient Ÿ 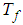 : Temperature of hot fluidŸ
: Temperature of hot fluidŸ 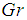 : Local thermal Grashof numberŸ
: Local thermal Grashof numberŸ 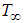 : Temperature of fluid far away from the plateŸ
: Temperature of fluid far away from the plateŸ 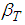 :Thermal expansion coefficientŸ
:Thermal expansion coefficientŸ 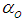 : Thermal diffusivityŸ
: Thermal diffusivityŸ 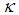 : Thermal conductivityŸ
: Thermal conductivityŸ 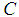 : ConcentrationŸ
: ConcentrationŸ 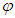 : Dimensionless concentrationŸ
: Dimensionless concentrationŸ 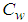 : Plate surface concentrationŸ
: Plate surface concentrationŸ 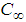 : Free stream concentrationŸ
: Free stream concentrationŸ 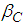 : Concentration expansion coefficientŸ
: Concentration expansion coefficientŸ 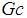 : Local Solutal Grashof numberŸ
: Local Solutal Grashof numberŸ 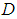 : Mass diffusivityŸ
: Mass diffusivityŸ 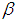 : Chemical reaction parameterŸ
: Chemical reaction parameterŸ 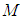 : Local Magnetic field parameterŸ
: Local Magnetic field parameterŸ 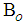 : Magnetic field strengthŸ
: Magnetic field strengthŸ 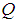 : Local heat source parameterŸ
: Local heat source parameterŸ 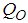 : Heat source parameterŸ
: Heat source parameterŸ 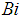 : Local convective heat transfer parameterŸ
: Local convective heat transfer parameterŸ 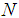 : Viscous dissipation parameterŸ
: Viscous dissipation parameterŸ 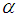 : Angle of inclinationŸ
: Angle of inclinationŸ 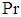 : Prandtl numberŸ
: Prandtl numberŸ 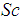 : Schmidt numberŸ
: Schmidt numberŸ 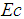 : Eckert numberŸ
: Eckert numberŸ 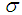 : Fluid electrical conductivityŸ
: Fluid electrical conductivityŸ 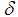 : Porosity parameter
: Porosity parameter2. Mathematical Formulation
- An incompressible ferrofluid such as polyethylene oxide solution is assumed to flow uniformly over a heated plate with applied transverse magnetic field. A Cartesian coordinate system is adopted with the origin fixed in such a way that the
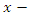 axis is taken along the direction of the flat surface and the
axis is taken along the direction of the flat surface and the 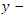 axis measured normal to the surface of the plate. Flow is induced by the combined effect of convection in the boundary layer and inclination. It is assumed that the viscous incompressible ferrofluid continuously flow over the heated flat plate with a uniform thickness h. The effect of viscous dissipation and chemical reaction are considered in this study. The flat plate is tilted to variable angles to study the effect of inclination on the flow regime as in Figure.1.
axis measured normal to the surface of the plate. Flow is induced by the combined effect of convection in the boundary layer and inclination. It is assumed that the viscous incompressible ferrofluid continuously flow over the heated flat plate with a uniform thickness h. The effect of viscous dissipation and chemical reaction are considered in this study. The flat plate is tilted to variable angles to study the effect of inclination on the flow regime as in Figure.1.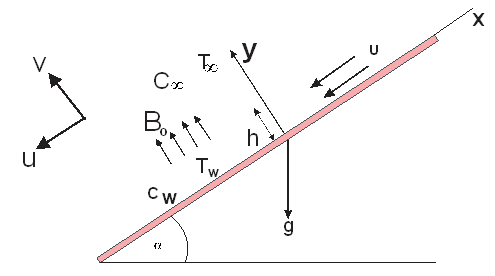 | Figure 1. Flow of a Ferrofluid over an Inclined Plate |
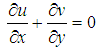 | (1) |
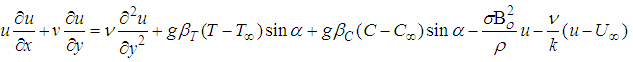 | (2) |
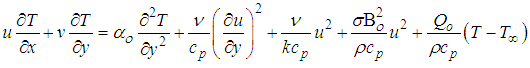 | (3) |
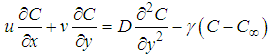 | (4) |
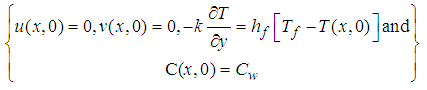 | (5) |
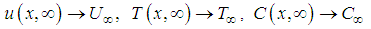 | (6) |
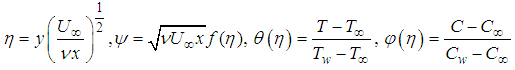 | (7) |
 and
and  are the dimensionless independent variable, stream function, temperature and concentration respectively. The stream function and the velocity components relate in the usual way as;
are the dimensionless independent variable, stream function, temperature and concentration respectively. The stream function and the velocity components relate in the usual way as;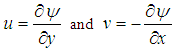 | (8) |
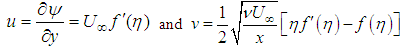 | (9) |
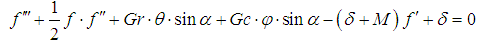 | (10) |
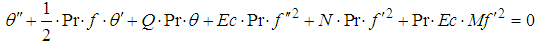 | (11) |
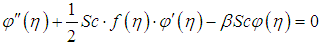 | (12) |
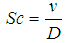 and
and 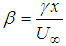
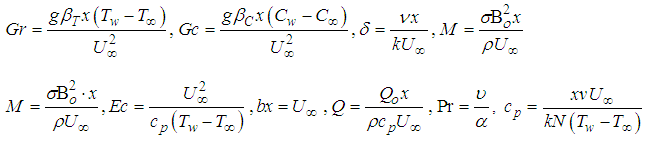 From (5) and (6) the corresponding dimensionless boundary conditions are:At the surface of the plate,
From (5) and (6) the corresponding dimensionless boundary conditions are:At the surface of the plate, 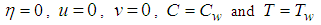
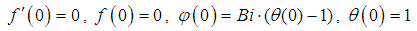 | (13) |
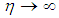 we obtained;
we obtained;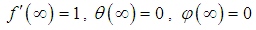 | (14) |
3. Order Reduction
- Equations (10-14) constitute a third order nonlinear boundary value problem. The boundary value problem is reduced to a first order initial value problem as follows:
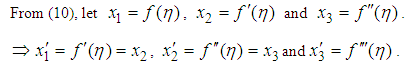
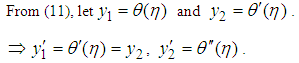
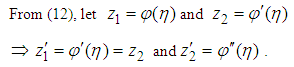 Hence the required first order system is;
Hence the required first order system is;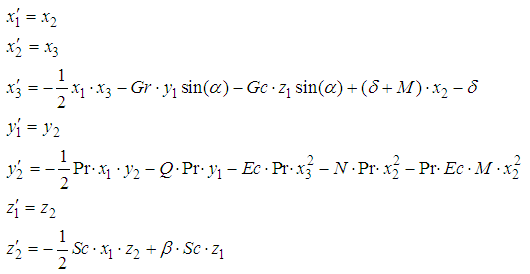 | (15) |
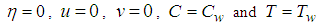 ;
;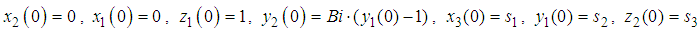 As
As 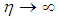 we obtained;
we obtained;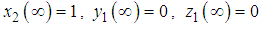
4. Numerical Results and Discussions
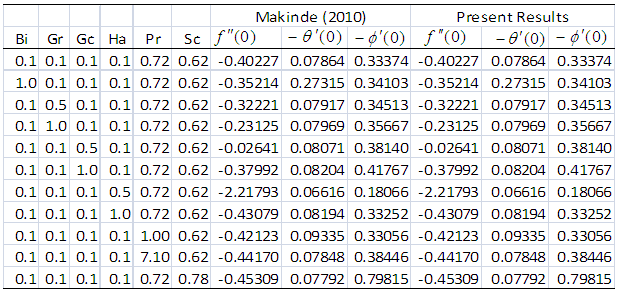
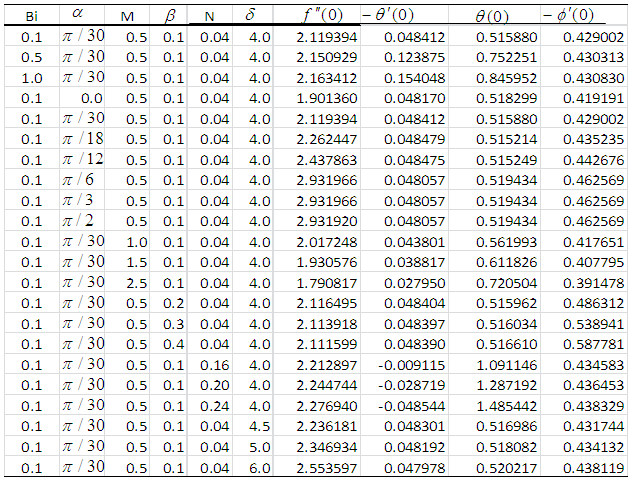
- The transformed dimensionless nonlinear ordinary differential equations (10-12) with boundary conditions (13) and (14) were further reduced to a first order system (15) and solved with Maple 16 using the fourth-order Runge-Kutta integration scheme with the Newton- Raphson shooting technique.The system of ordinary differential equations was simulated under similar conditions to previously published work of Makinde and Olanrewaju [19]. A comparison of results shows an excellent agreement in Table 1. An excellent agreement was also observed when simulated under similar conditions and compared with Makinde [18] in Table 2, validating the procedure.
|
|
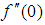 , the Nusselt number
, the Nusselt number 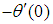 , temperature
, temperature 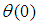 , as well as the Sherwood number
, as well as the Sherwood number 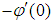 have been discussed.Graphical results have also been illustrated for velocity, temperature and concentration profiles in the boundary layer region.It is observed in Table 3 that increasing the Biot number (Bi) increases the skin friction coefficient, the Nusselt and Sherwood numbers as well as the temperature of the fluid in the boundary layer. Thus, increasing the Biot number implies an increase in the heat transfer coefficient which enhances buoyancy in the boundary layer. Interaction between agitated fluid molecules and the surface of the plate results in increased shear stresses hence increasing the skin friction coefficient and temperature in the boundary layer.It is also observed that increasing the angle of inclination has a dual effect of decreasing and increasing the temperature and skin friction coefficient in the boundary layer as in Table 3. It can be observed that increasing the angle of inclination from
have been discussed.Graphical results have also been illustrated for velocity, temperature and concentration profiles in the boundary layer region.It is observed in Table 3 that increasing the Biot number (Bi) increases the skin friction coefficient, the Nusselt and Sherwood numbers as well as the temperature of the fluid in the boundary layer. Thus, increasing the Biot number implies an increase in the heat transfer coefficient which enhances buoyancy in the boundary layer. Interaction between agitated fluid molecules and the surface of the plate results in increased shear stresses hence increasing the skin friction coefficient and temperature in the boundary layer.It is also observed that increasing the angle of inclination has a dual effect of decreasing and increasing the temperature and skin friction coefficient in the boundary layer as in Table 3. It can be observed that increasing the angle of inclination from 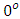 to
to 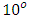 increases the Nusselt number and decreases the temperature and above
increases the Nusselt number and decreases the temperature and above 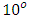 caused a decrease in the Nusselt number and increased temperature. However, increasing the angle of inclination generally results in increased Sherwood number. The skin friction also increased when the angle of inclination was increased between
caused a decrease in the Nusselt number and increased temperature. However, increasing the angle of inclination generally results in increased Sherwood number. The skin friction also increased when the angle of inclination was increased between 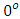 and
and 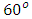 and decreased above
and decreased above 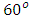 . Increasing the magnetic field parameter significantly decreased the skin friction coefficient, Nusselt number and Sherwood number but increased the temperature of the fluid within the boundary layer. The magnetic field produces a Lorenz force which retards the motion of the fluid and reduces buoyancy; hence the heat transferred remains trapped in the boundary layer causing the rise in temperature as shown in Table 3.Again in Table 3, increasing the chemical reaction parameter caused a decrease in the skin friction coefficient and the Nusselt number but increased the Sherwood number and temperature. The fluid temperature increased due to exothermic reaction and reduced buoyancy of fluid molecules. Increasing the viscous dissipation and porosity parameters increased the local skin friction coefficient, the Sherwood number and the temperature of the fluid but decreased the Nusselt number. The increased temperature is associated with both parameters because they enhance interaction between molecules of the fluid and the plate’s surface as observed in Table 3.It is observed in Table 4 that increasing the Prandtl, Eckert numbers and local heat generation parameter significantly increased the local skin friction coefficient. The Sherwood number and the temperature of the fluid also increased when the Prandtl, Eckert numbers and the local heat generation parameters were increased. However it resulted in a decreased Nusselt number.It is again observed in Table 4 that increases in both thermal and solutal Grashof numbers increased the skin friction coefficient, the Sherwood number and the Nusselt number, resulting in marginal decreases in wall temperature of the plate. An increase in each of these parameters improves buoyancy and convection, which enable fluid molecules to efficiently move away from the plate’s surface leading to reduction in temperature. However shear stresses between the energetic molecules and the surface of the inclined plate accounts for the increased skin friction coefficient.We further observed that increases in Schmidt number decreased the local skin friction coefficient and the Nusselt number but increased the Sherwood number and plate’s wall temperature as depicted numerically in Table 4.
. Increasing the magnetic field parameter significantly decreased the skin friction coefficient, Nusselt number and Sherwood number but increased the temperature of the fluid within the boundary layer. The magnetic field produces a Lorenz force which retards the motion of the fluid and reduces buoyancy; hence the heat transferred remains trapped in the boundary layer causing the rise in temperature as shown in Table 3.Again in Table 3, increasing the chemical reaction parameter caused a decrease in the skin friction coefficient and the Nusselt number but increased the Sherwood number and temperature. The fluid temperature increased due to exothermic reaction and reduced buoyancy of fluid molecules. Increasing the viscous dissipation and porosity parameters increased the local skin friction coefficient, the Sherwood number and the temperature of the fluid but decreased the Nusselt number. The increased temperature is associated with both parameters because they enhance interaction between molecules of the fluid and the plate’s surface as observed in Table 3.It is observed in Table 4 that increasing the Prandtl, Eckert numbers and local heat generation parameter significantly increased the local skin friction coefficient. The Sherwood number and the temperature of the fluid also increased when the Prandtl, Eckert numbers and the local heat generation parameters were increased. However it resulted in a decreased Nusselt number.It is again observed in Table 4 that increases in both thermal and solutal Grashof numbers increased the skin friction coefficient, the Sherwood number and the Nusselt number, resulting in marginal decreases in wall temperature of the plate. An increase in each of these parameters improves buoyancy and convection, which enable fluid molecules to efficiently move away from the plate’s surface leading to reduction in temperature. However shear stresses between the energetic molecules and the surface of the inclined plate accounts for the increased skin friction coefficient.We further observed that increases in Schmidt number decreased the local skin friction coefficient and the Nusselt number but increased the Sherwood number and plate’s wall temperature as depicted numerically in Table 4.
|
|
5. Graphical Results and Discussions
5.1. Effects of Parameter Variation on Velocity Profiles
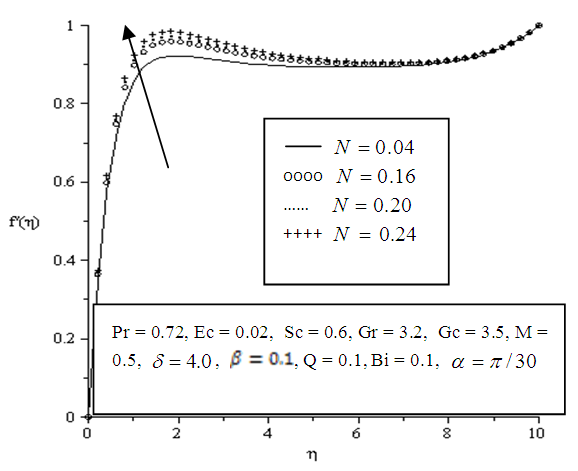
- The effects of parameter variation on the velocity profile in the boundary layer are shown below in Figures 5.1 - 5.10. Velocity at wall is zero but generally increases away from the plate surface satisfying the no slip condition.In Figure 5.1 increasing the value of the angle of inclination tends to sharply increase the velocity of the fluid within the boundary layer. Also a significant increase in velocity is observed when the viscous dissipation, thermal Grashof, solutal Grashof, local heat generation, Eckert number, Biot number and porosity parameters are increased as depicted in Figures 5.2, 5.3, 5.4, 5.6, 5.7, 5.8 and 5.9 respectively. The increased velocity is as a result of the inclination and buoyancy which is induced by convection in the boundary layer. The inclination also facilitated efficient transport and distribution of heat and mass.It is also observed that increasing the magnetic parameter greatly decreased velocity in the boundary layer as displayed in Figure 5.5.
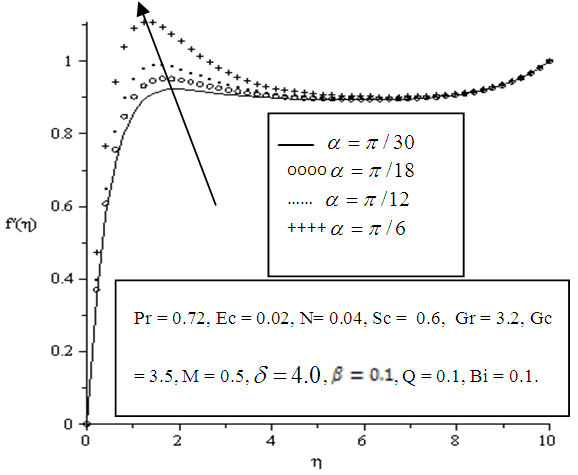 | Figure 5.1. Effect of variation of angle of inclination 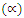 on velocity profile on velocity profile |
 | Figure 5.2. Effect of variation of viscous dissipation parameter (N) on velocity profile |
 | Figure 5.3. Effect of variation of thermal Grashof number (Gr) on velocity profile |
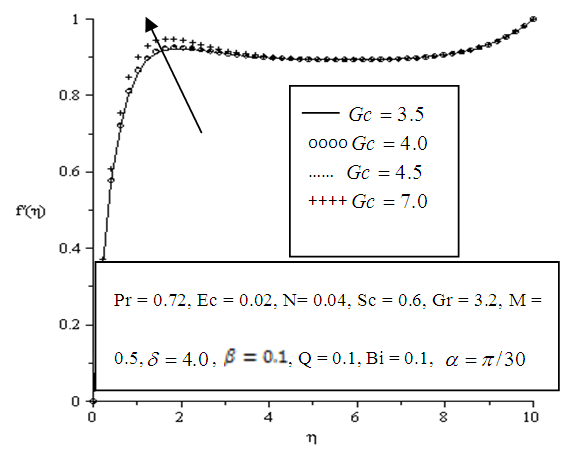 | Figure 5.4. Effect of variation of solutal Grashof number (Gc) on velocity profile |
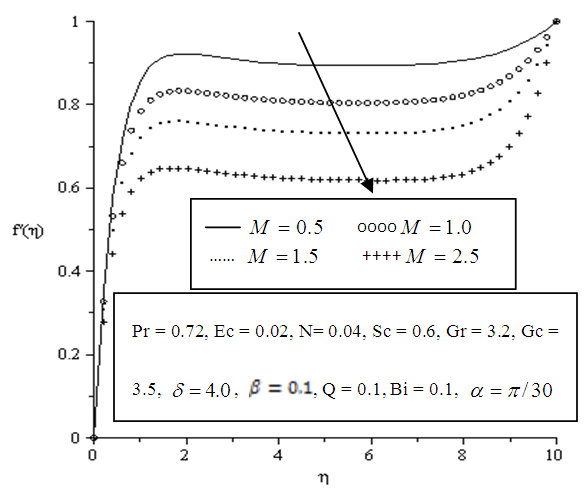 | Figure 5.5. Effect of variation of Magnetic Parameter (M) on velocity profile |
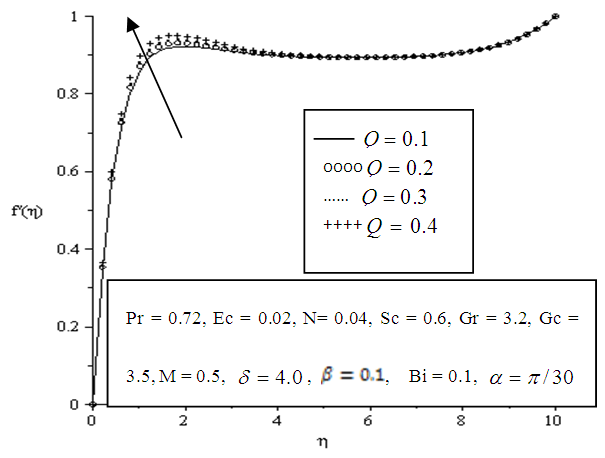 | Figure 5.6. Effect of variation of Local heat source parameter (Q) on velocity profile |
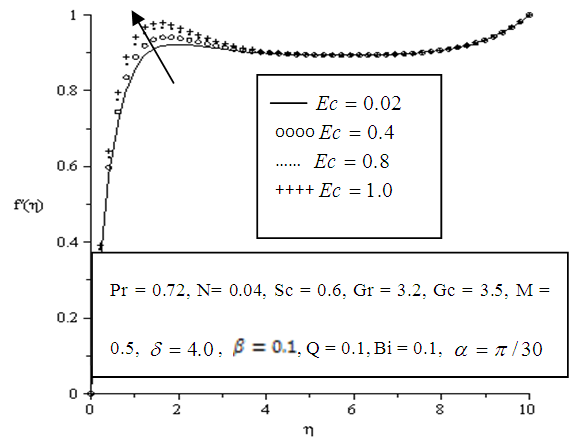 | Figure 5.7. Effect of variation of Eckert number (Ec) on velocity profile |
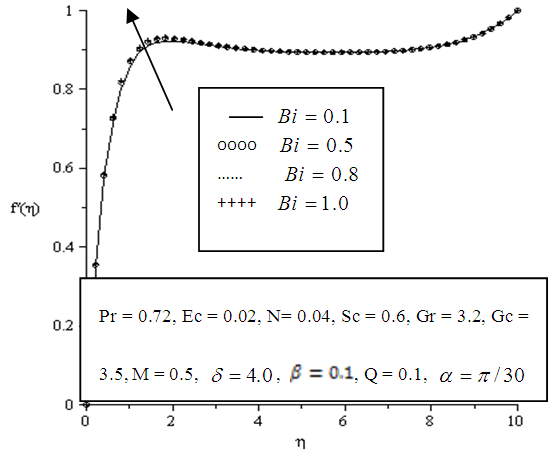 | Figure 5.8. Effect of variation of Biot number (Bi) on velocity profile |
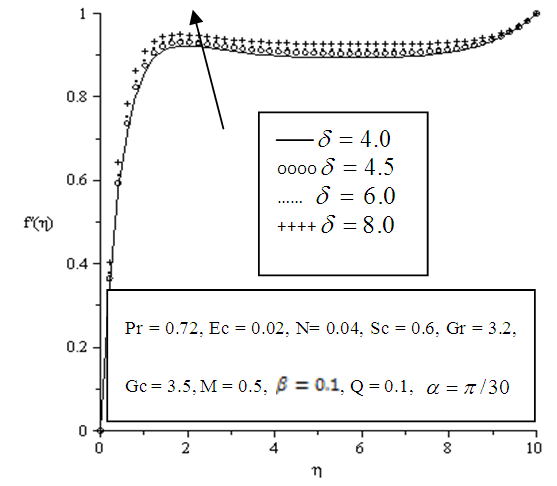 | Figure 5.9. Effect of variation of Porosity 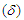 on velocity profile on velocity profile |
5.2. Effects of Parameter Variation on Temperature Profiles
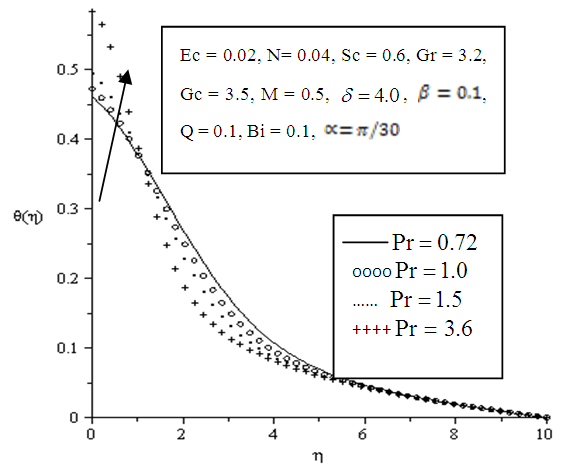
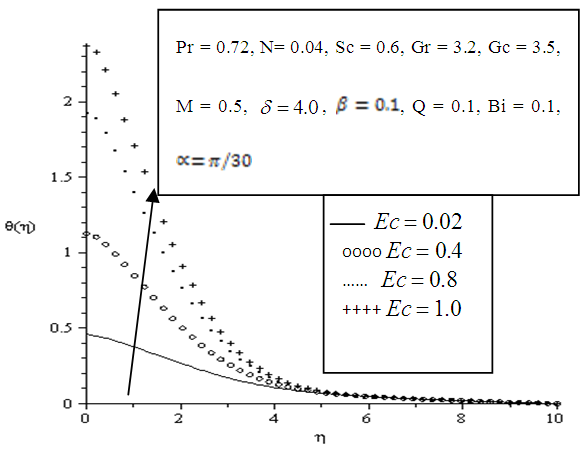
- The effects of parameters variation on the temperature profile are shown in Figures 5.10 - 5.16. The temperature exponentially decays away from the plate surface to attain a value of zero denoting the temperature of the cooling fluid far away from the plate surface. Increasing the angle of inclination resulted in decreased temperature, this is observed as a descent graphically displayed in figure 5.10. The temperature drop resulted from the increased velocity which enhanced convection and heat dissipation. It is also observed that increasing the Prandtl number, Eckert number, viscous dissipation parameter, local heat generation parameter and Biot number significantly increased the temperature of the plate, thickening the thermal boundary layer at the wall of the plate as depicted in figures 5.11, 5.12, 5.13, 5.15 and 5.16 respectively. In Figure 5.14, an increase in the Schmidt number had no great effect on the temperature of the plate however it also results in slight thickening of the thermal boundary layer.
 | Figure 5.10. Effect of variation of angle of inclination 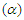 on Temperature profile on Temperature profile |
 | Figure 5.11. Effect of variation of Prandtl number (Pr) on Temperature profile |
 | Figure 5.12. Effect of variation of Eckert number on Temperature profile |
 | Figure 5.13. Effect of variation of viscous dissipation parameter (N) on Temperature profile |
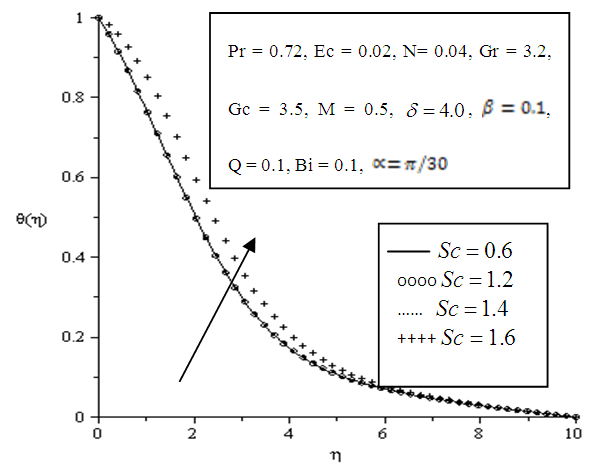 | Figure 5.14. Effect of variation of Schmidt number (Sc) on Temperature profile |
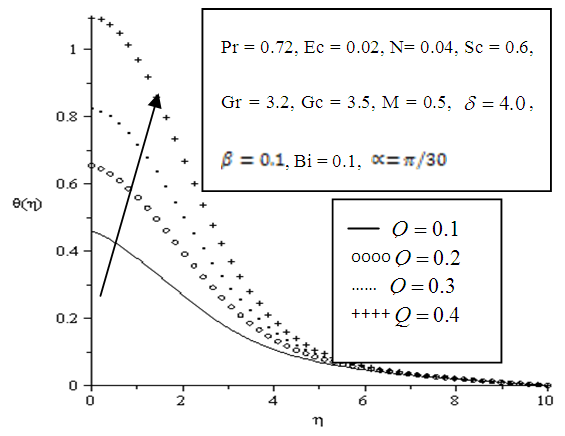 | Figure 5.15. Effect of variation of Local heat generation parameter (Q) on Temperature profile |
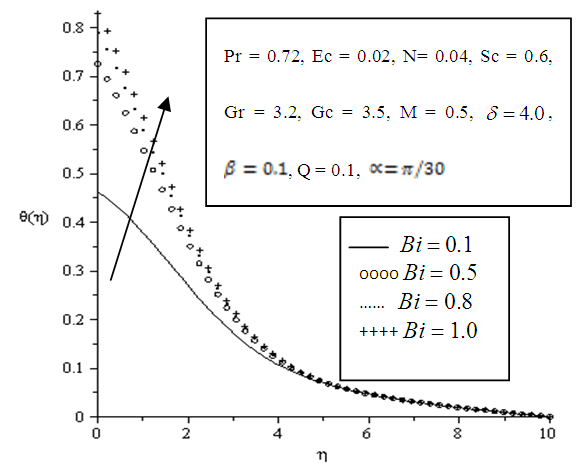 | Figure 5.16. Effect of variation of Biot number (Bi) on Temperature profile |
5.3. Effects of Parameter Variation on Concentration Profiles
- Figures 5.17 - 5.20 depict the effects of variation of parameters on the thickness of the concentration boundary layer. Concentration at the wall is greatest assuming a value of one and exponentially decaying to zero indicating decreased concentration at free stream.A reduction in thickness of the concentration boundary layer is observed upon increasing the angle of inclination, Schmidt number and Chemical reaction parameter as displayed in Figures 5.17, 5.18 and 5.20 respectively. The decay of the thickness of the concentration boundary layer is as a result of increased velocity and molecular diffusion. The thinning of the concentration boundary layer indicates efficient transport of mass of fluid.
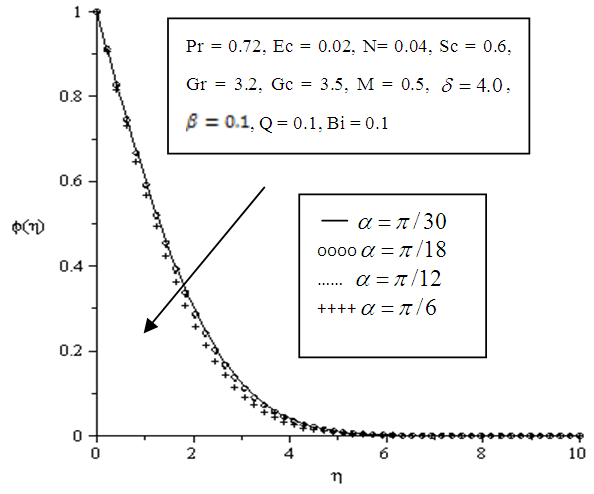 | Figure 5.17. Effect of variation of angle of inclination on Concentration profile |
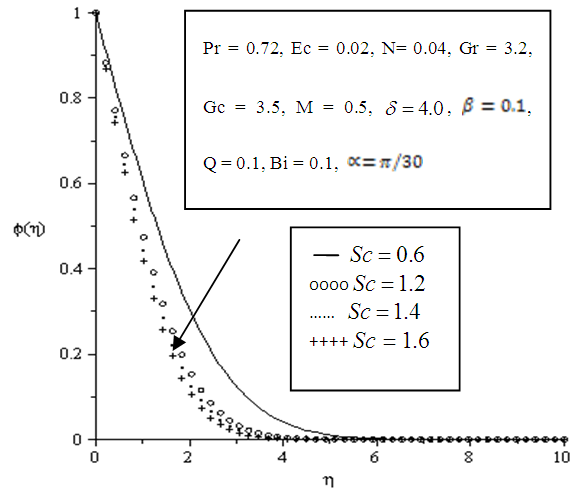 | Figure 5.18. Effect of variation of Schmidt number on Concentration profile |
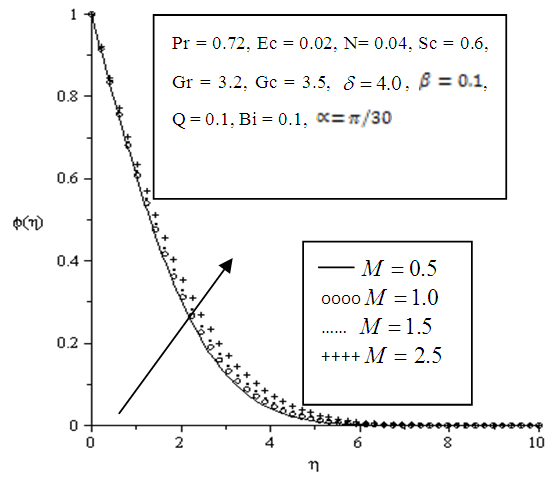 | Figure 5.19. Effect of variation of Magnetic Parameter on Concentration profile |
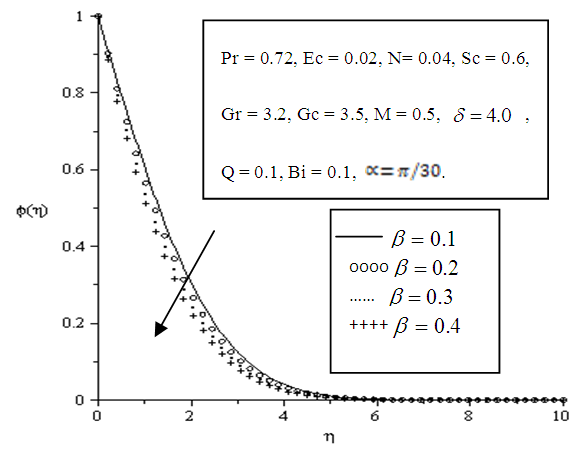 | Figure 5.20. Effect of variation of Chemical Reaction Parameter on Concentration profile |
6. Conclusions
- In this paper the effect of inclination and variation of other controlling thermo-physical parameters have been studied and their effects presented. Applications of effects of some parameters are recommended for cooling and heating in industrial processes. It has been established that the angle of inclination affects the heat and mass transfer characteristics of a semi-infinitely heated plate. An increase in the angle of inclination had a considerable effect on the flow field. This manifested as an increased in velocity of fluid and decreased temperature of plate within some ranges of inclination.The effects of increasing values of the thermo-physical parameters which had significant effect on the velocity, temperature and concentration profiles are summarized as follows:i. The velocity significantly increases with the increase in the angle of inclination
 . The velocity also increased when other parameters such as viscous dissipation (N), thermal Grashof number (Gr), Solutal Grashof number (Gc), Porosity
. The velocity also increased when other parameters such as viscous dissipation (N), thermal Grashof number (Gr), Solutal Grashof number (Gc), Porosity 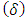 , Eckert number (Ec), Biot number (Bi) and local heat generation (Q) were increased. A decrease in velocity was also observed when the magnetic field parameter (M) was increased. ii. The temperature also decreased significantly when the angle of inclination was increased from
, Eckert number (Ec), Biot number (Bi) and local heat generation (Q) were increased. A decrease in velocity was also observed when the magnetic field parameter (M) was increased. ii. The temperature also decreased significantly when the angle of inclination was increased from 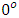 to
to 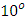 (“cooling angle”) and increased when the angle of inclination was greater than
(“cooling angle”) and increased when the angle of inclination was greater than 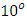 . The temperature decreased when both thermal and solutal Grashof numbers (Gr) and (Gc) respectively were increased. However a rise in temperature was observed when the Prandtl number (Pr), Eckert number (Ec), Biot number (Bi), viscous dissipation parameter (N), Schmidt number (Sc) and local heat generation Parameter (Q) were increased. The concentration in the boundary layer decreased with increased angle of inclination
. The temperature decreased when both thermal and solutal Grashof numbers (Gr) and (Gc) respectively were increased. However a rise in temperature was observed when the Prandtl number (Pr), Eckert number (Ec), Biot number (Bi), viscous dissipation parameter (N), Schmidt number (Sc) and local heat generation Parameter (Q) were increased. The concentration in the boundary layer decreased with increased angle of inclination 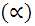 . A decreased concentration was also observed when the chemical reaction paraeter
. A decreased concentration was also observed when the chemical reaction paraeter 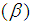 , the Schmidt number
, the Schmidt number 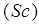 , thermal Grashof number
, thermal Grashof number 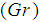 , solutal Grashof number
, solutal Grashof number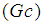 and Biot number
and Biot number 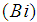 were increased. However an increase in concentration in the boundary layer was observe when the magnetic field parameter (M) was increased. It is therefore recommended that;Ÿ In applying the technique of inclination to enhance cooling of materials in industrial processes, the range of the “cooling angle” should be considered. Ÿ The chemical reaction parameter and Schmidt number which enhances mass diffusivity should be considered in processes involving fluid transportation.Ÿ The viscous dissipation parameter had an integral effect in increasing the temperature in the boundary layer and should be considered in the design of heating systems.
were increased. However an increase in concentration in the boundary layer was observe when the magnetic field parameter (M) was increased. It is therefore recommended that;Ÿ In applying the technique of inclination to enhance cooling of materials in industrial processes, the range of the “cooling angle” should be considered. Ÿ The chemical reaction parameter and Schmidt number which enhances mass diffusivity should be considered in processes involving fluid transportation.Ÿ The viscous dissipation parameter had an integral effect in increasing the temperature in the boundary layer and should be considered in the design of heating systems.ACKNOWLEDGEMENTS
- The authors are very grateful to the reviewer(s) for the valuable comments and suggestions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML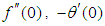 and
and 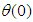 for values of Bi, Gr and Pr when
for values of Bi, Gr and Pr when 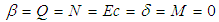 and
and 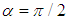
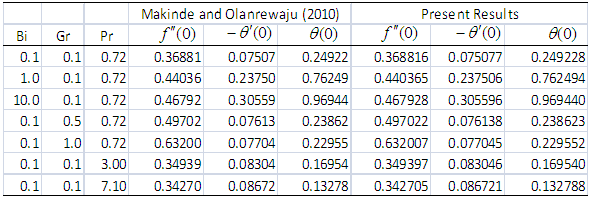
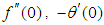 and
and 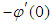 for values of Bi, Gr, Gc, Pr and Sc when
for values of Bi, Gr, Gc, Pr and Sc when 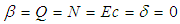 and
and 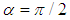
 , M=0.5,
, M=0.5,  , N = 3.2, and
, N = 3.2, and