-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(3): 144-147
doi:10.5923/j.ajcam.20160603.04

Refined Iterative Method for Solving System of Linear Equations
Genanew Gofe Gonfa
Department of Mathematics, College of Natural Science, Jimma University, Ethiopia
Correspondence to: Genanew Gofe Gonfa , Department of Mathematics, College of Natural Science, Jimma University, Ethiopia.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, the refined iterative method namely, refinement of generalized Gauss-Seidel (RGGS) method for solving systems of linear equations is studied. Sufficient conditions for convergence are given and some numerical experiments are considered to show the efficiency of the method. The result shows that RGGS method converges if the coefficient matrix is diagonally dominant (DD) or an M- matrix for any initial vectors, moreover it is more efficient than the other methods Refinement of generalized Jacobi (RGJ) and successive-over relaxation (SOR) methods, considering their performance, using parameters such as time to converge, number of iterations required to converge and level of accuracy.
Keywords: Generalized Gauss-Seidel Method, M-matrix, Row strictly diagonally dominant matrix, Convergence
Cite this paper: Genanew Gofe Gonfa , Refined Iterative Method for Solving System of Linear Equations, American Journal of Computational and Applied Mathematics , Vol. 6 No. 3, 2016, pp. 144-147. doi: 10.5923/j.ajcam.20160603.04.
Article Outline
1. Introduction
- Consider the linear systems of equations
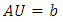 | (1.1) |
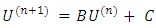 | (1.2) |
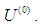 On the other hand [1] developed the method called generalized Gauss-Seidel method and the result shows that the method is more efficient than conventional Gauss-Seidel method. Author [2], indicated that the basic idea behind the first order stationary iterative method is how to write Eq. (1.2) and the choice of initial approximation to guarantee the convergence of the method. In this paper, the generalized Gauss-Seidel method is refined and compared its efficiency with the other methods.Some of the basic definition of terms used in the this paper given here as underDefinition 1: A matrix A is said to be an M-matrix if it satisfies the following four properties
On the other hand [1] developed the method called generalized Gauss-Seidel method and the result shows that the method is more efficient than conventional Gauss-Seidel method. Author [2], indicated that the basic idea behind the first order stationary iterative method is how to write Eq. (1.2) and the choice of initial approximation to guarantee the convergence of the method. In this paper, the generalized Gauss-Seidel method is refined and compared its efficiency with the other methods.Some of the basic definition of terms used in the this paper given here as underDefinition 1: A matrix A is said to be an M-matrix if it satisfies the following four properties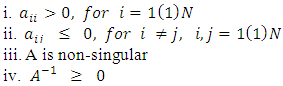 Definition 2: A banded matrix is a square matrix with zeros after “m” elements above and below the main diagonal, where m is less than the size of the matrix (i.e if the matrix is
Definition 2: A banded matrix is a square matrix with zeros after “m” elements above and below the main diagonal, where m is less than the size of the matrix (i.e if the matrix is  then
then 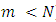 ). In this case where bandedness mater, “m” is usually significantly less than N.
). In this case where bandedness mater, “m” is usually significantly less than N.2. Preliminary
- Considering the system of equations given in Eq. (1.1) and using splitting procedures in [1], we obtain:
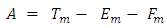 | (2.1) |
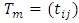 be a banded matrix of band width 2m+1 defined as
be a banded matrix of band width 2m+1 defined as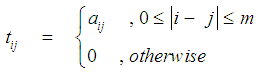
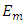 and
and 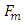 are strictly lower and upper triangular part of the matrix
are strictly lower and upper triangular part of the matrix 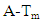 respectively, and defined as follows.
respectively, and defined as follows. Then, the Generalized Gauss-Seidel method for the solution of Eq. (1.1) is defined as
Then, the Generalized Gauss-Seidel method for the solution of Eq. (1.1) is defined as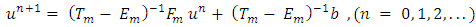 | (2.2) |
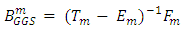 is generalized Gauss-Seidel iteration matrix and
is generalized Gauss-Seidel iteration matrix and 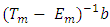 its corresponding iteration vector.
its corresponding iteration vector.3. Description of the Method
- Meaningful modifications of the iterative matrix will reduce the spectral radius and increases the rate of convergence of the method, [5] and [7]. The objective of this section is to develop refinement of generalized Gauss-Seidel (RGGS). Assume
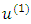 be an initial approximation for the solution of the linear system Eq. (1.1), and
be an initial approximation for the solution of the linear system Eq. (1.1), and 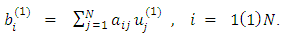 After n iterations, we can have
After n iterations, we can have 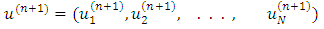 it implies that
it implies that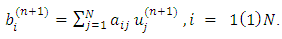 Now we refine this to obtain solution as
Now we refine this to obtain solution as 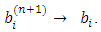 Let
Let 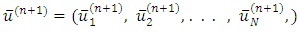 be an approximation for the solution of linear system Eq. (1.1). i.e;
be an approximation for the solution of linear system Eq. (1.1). i.e; 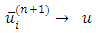 where u is the exact solution of Eq. (1.1). Here all
where u is the exact solution of Eq. (1.1). Here all 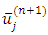 are unknown, so we define it as
are unknown, so we define it as 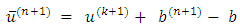 | (3.1) |
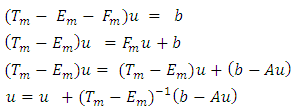 | (3.2) |
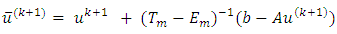 Further, from Eq. (2.2), we obtain
Further, from Eq. (2.2), we obtain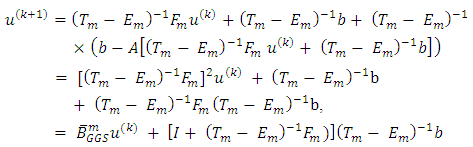 | (3.3) |
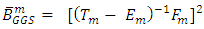 is the refinement of generalized Gauss-Seidel iteration matrix.
is the refinement of generalized Gauss-Seidel iteration matrix.4. Condition on the Convergence of the Method
- Theorem 1:- Let A be a strictly diagonally dominant (SDD) matrix. Then for any natural number
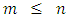 the GGS method is convergent for any initial guess
the GGS method is convergent for any initial guess 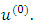 Proof: - see [1]Theorem 2:- Let
Proof: - see [1]Theorem 2:- Let 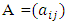 be an M-matrix. Then for a given natural number
be an M-matrix. Then for a given natural number 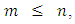 generalized Gauss-Seidel method is convergent for any initial guess
generalized Gauss-Seidel method is convergent for any initial guess 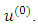 Proof: - see [1].Theorem 3:- If A is strictly diagonally dominant matrix then the refinement of generalized Gauss-Seidel method converges for any choice of the initial approximation
Proof: - see [1].Theorem 3:- If A is strictly diagonally dominant matrix then the refinement of generalized Gauss-Seidel method converges for any choice of the initial approximation 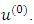 Proof:- Let
Proof:- Let 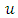 be the exact solution of Eq. (1.1) and A be SDD matrix. Then generalized Gauss- Seidel method is convergent as proved by [1]. If
be the exact solution of Eq. (1.1) and A be SDD matrix. Then generalized Gauss- Seidel method is convergent as proved by [1]. If 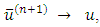 then
then 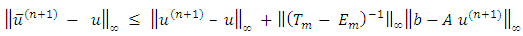 From Theorem 4.1,
From Theorem 4.1, 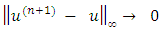 likewise we have
likewise we have 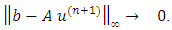 Therefore,
Therefore, 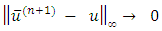 Hence refinement of generalized Gauss-Seidel method is convergent.Theorem 4:- let
Hence refinement of generalized Gauss-Seidel method is convergent.Theorem 4:- let 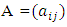 be an M-matrix. Then for a given natural number
be an M-matrix. Then for a given natural number 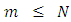 , the refinement of generalized Gauss-Seidel method converges for any choice of the initial approximation
, the refinement of generalized Gauss-Seidel method converges for any choice of the initial approximation 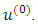 Proof:- It follows from Theorem 2 and Theorem 3.Theorem 5:- If A is row strictly diagonally dominant matrix then
Proof:- It follows from Theorem 2 and Theorem 3.Theorem 5:- If A is row strictly diagonally dominant matrix then 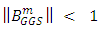 Proof:- By Theorem 1 and convergence Theorem given by [4],
Proof:- By Theorem 1 and convergence Theorem given by [4], 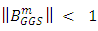 Theorem 6:- i) If A is SDD matrix, then
Theorem 6:- i) If A is SDD matrix, then 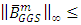
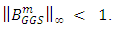 ii) If A is an M- matrix, then
ii) If A is an M- matrix, then 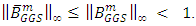 Proof:-i) By the convergence Theorem of [4], we have
Proof:-i) By the convergence Theorem of [4], we have 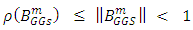 where
where 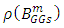 is the spectral radius of generalized Gauss-Seidel method. Again by Theorem 5, we have
is the spectral radius of generalized Gauss-Seidel method. Again by Theorem 5, we have 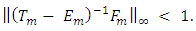 | (4.1) |
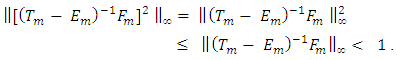 Therefore,
Therefore, 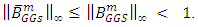 ii) Similar to (i) above, one can complete the proof the Theorem.Remark: - We observe that the iterative matrix of refinement of generalized Gauss-Seidel is the square of generalized Gauss-Seidel iterative matrix. i.e.
ii) Similar to (i) above, one can complete the proof the Theorem.Remark: - We observe that the iterative matrix of refinement of generalized Gauss-Seidel is the square of generalized Gauss-Seidel iterative matrix. i.e. 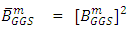 . As it can be easily realized
. As it can be easily realized 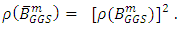 If GGS method converges
If GGS method converges 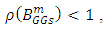 then
then 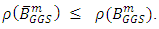 Thus, if the GGS and RGGS method converge, the RGGS method converges faster than the GGS method.
Thus, if the GGS and RGGS method converge, the RGGS method converges faster than the GGS method.5. Numerical Experiments
- The major factors to be considered in comparing different numerical methods are the accuracy of numerical solution and its computational time, [9]. The same author, indicated that the comparison of numerical methods is not simply because of their performance may depend on the characteristic of the problem at hand. It should also be noted that there are other factors to be considered, such as stability, versatility, proof against run-time error, and so on which are being considered in most of the MATLAB built-in routines, [10]. Upon this, the efficiency of RGGS was compared with SOR and RGJ of [5] by considering two model problems in which it reduced to system of linear equations of which its coefficient matrix is either M-matrix or diagonal dominant matrix and also it illustrate the theory developed in this paper. Data about iteration number and computational times (in seconds) obtained using RGGS, SOR and RGJ is used for the analysis of the result. 1. Consider the system of linear equations, which obtained from the finite difference approximation of the mixed boundary value problem considered by Jain and et al [8] on page 106.
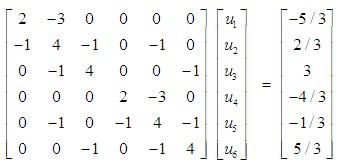 2. Consider a system of linear equations, which is reduced from the boundary value problem,
2. Consider a system of linear equations, which is reduced from the boundary value problem, 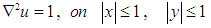 where
where 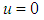 on the boundary. By applying Galerkin Method with triangular element and considering the symmetry of the boundary, Jain and et al [8].
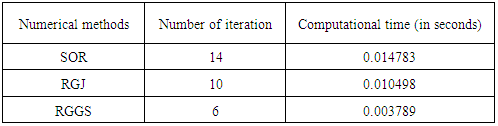
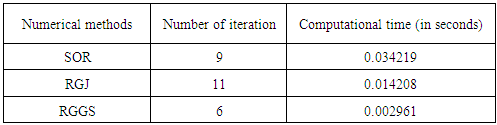
on the boundary. By applying Galerkin Method with triangular element and considering the symmetry of the boundary, Jain and et al [8]. The coefficient matrix of the first example is an M-Matrix whereas the second one is diagonal dominant for which the mentioned methods are convergent for any initial vector. Results produced by the two linear systems of equation are given in the Tables 1 and 2 respectively.
The coefficient matrix of the first example is an M-Matrix whereas the second one is diagonal dominant for which the mentioned methods are convergent for any initial vector. Results produced by the two linear systems of equation are given in the Tables 1 and 2 respectively.
|
|
6. Discussion and Conclusions
- The Refinement of Generalized Gauss-Seidel method for solving linear systems of equation has been presented. Two examples, which obtained from boundary value problems and reduced to systems of linear equations of 6 x6 and 4 x 4 by finite difference approximation and finite element method respectively, were studied using MATLAB version 7.60(R2008a) software. The results obtained by Refinement of generalized Gauss-Seidel are compared with that of Refinement of generalized Jacobi and Successive-Over Relaxation as presented by Table 1 and Table 2. The analysis of results shows that RGGS method takes shorter time, 0.003789 seconds and 0.002961 seconds for the 6 x 6 and 4 x 4 linear equations respectively. In terms of number of iterations required to converge to the exact solution, the RGGS method takes about 6 iteration for each problem as compared to other methods, namely; SOR (14 iteration for 6x6 and 9 iteration for 4x4 system of equations) and RGJ (10 iteration for 6x6 and 11 iteration for 4x4 system of equations) with 510-6 error of tolerance. On the other hand, methods which register small number of iteration demands less computer storage to store its data, [3], as a result RGGS demands less computer storage to store its data relative to SOR and RGJ. Thus, in all the parameters considered in this paper, i.e. CPU runtime, number of iteration and memory storage, the Refinement of generalized Gauss- Seidel is more efficient than the other methods considered when the coefficient matrix is either an M-matrix or diagonal dominant matrix.
ACKNOWLEDGEMENTS
- The author would like to express his sincere gratitude to Dr. Gemechis File for constructive comments during the development of this paper and the acknowledgement also goes to Mr. Hailu Muleta for a kind cooperation while coding the iteration of the examples on MatLab Software.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML