-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(3): 136-143
doi:10.5923/j.ajcam.20160603.03

The Revised New Iterative Method for Solving the Model Describing Biological Species Living Together
Ibrahim Hassan 1, Akeremale Olusola Collins 1, Onwubuya Isaac Obiajulu 2
1Department of Mathematics, Federal University, Lafia, Nigeria
2Department of Mathematics/Statistics/Computer Science, University of Agriculture Makurdi, Nigeria
Correspondence to: Ibrahim Hassan , Department of Mathematics, Federal University, Lafia, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, a system of two nonlinear delay integro-differential equations derived from considering biological species living together and the revised new iterative method proposed by Bhalekar and Daftardar-Gejji (2012) is implemented for finding the solution of this system. Also, to demonstrate the validity and applicability of the method, examples are presented and results are compared with Adomian decomposition method, Variational iteration method, Pseudospectral method, and the Taylor collocation method. The method yields a series with accelerated convergence.
Keywords: New iterative method, Nonlinear integro-differential equation, Revised new iterative method, Variational iteration method, Adomian decomposition method, Pseudospectral Lengendre method, Taylor collocation method
Cite this paper: Ibrahim Hassan , Akeremale Olusola Collins , Onwubuya Isaac Obiajulu , The Revised New Iterative Method for Solving the Model Describing Biological Species Living Together, American Journal of Computational and Applied Mathematics , Vol. 6 No. 3, 2016, pp. 136-143. doi: 10.5923/j.ajcam.20160603.03.
Article Outline
1. Introduction
- System of Volterra Integro-differential equation (IDEs) arise in scientific fields such as biology [1], Medicine [2], Ecology [4], Population growth [3], physics such as electromagnetism theory [5], one dimensional visco elasticity and reactor dynamics [6]. This class of equations plays an important role in modelling of various problems of engineering and natural science and hence, attracted much attention in numerical computation and analysis. This paper is concerned with the dynamic of two interacting species which was first modelled by [7]. It is considered two separated two species with number
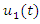 and
and 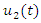 at time
at time 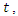 where first species increases and second decreases. If they put together that the second species will feed on the first, there will be increase in the rate of the second species
where first species increases and second decreases. If they put together that the second species will feed on the first, there will be increase in the rate of the second species 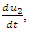 which depends not only on the present population
which depends not only on the present population 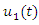 but also on all previous values of the first species. When a steady-state or equilibrium is reached between the two species, it is described by the following system of nonlinear delay Volterra Integro-differential equations:
but also on all previous values of the first species. When a steady-state or equilibrium is reached between the two species, it is described by the following system of nonlinear delay Volterra Integro-differential equations: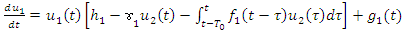 | (1) |
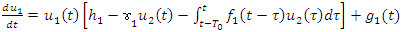 | (2) |
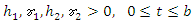 with initial conditions
with initial conditions 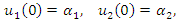 | (3) |
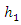 and
and 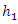 are coefficients of increase and decrease of the first and the second species respectively. The parameters
are coefficients of increase and decrease of the first and the second species respectively. The parameters 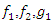 and
and 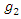 are given functions while
are given functions while 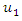 and
and 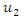 are unknown functions and
are unknown functions and 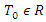 is assumed to be the finite heredity duration of both species.Several numerical methods of approximating the solution of this model are known; Adomian decomposition method (ADM) [9], Variational Iteration Method (VIM) [10], Legendre Multiwavelent Method (LMM) [11], Differential Transform Method (DTM) [12] and Taylor Collocation Method (TCM) [13]. Recently, [14] have introduced a new Iterative Method (NIM) to solve general functional equation:
is assumed to be the finite heredity duration of both species.Several numerical methods of approximating the solution of this model are known; Adomian decomposition method (ADM) [9], Variational Iteration Method (VIM) [10], Legendre Multiwavelent Method (LMM) [11], Differential Transform Method (DTM) [12] and Taylor Collocation Method (TCM) [13]. Recently, [14] have introduced a new Iterative Method (NIM) to solve general functional equation: 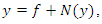 where
where 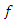 is specified function and
is specified function and 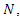 a given nonlinear function of
a given nonlinear function of 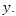 [15] obtained the solution of
[15] obtained the solution of 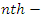 order linear and nonlinear Integro-differential equation using NIM. [16] applied NIM to system of Volterra Integro-differential equationsNIM is simple in its principles and easy to implement on computer packages such as Mathematica and Maple. This method is better than numerical methods as it is free from rounding off errors and does not require large computer power. NIM has proven successful over other methods in many cases [17], [18] [19], [20] [21], [22], [16].Bhaleker, S. and Datterder-Gejj, V. [18] presented a modification of the NIM called the Revised NIM (RNIM), to solve the following system of functional equations with improved convergence:
order linear and nonlinear Integro-differential equation using NIM. [16] applied NIM to system of Volterra Integro-differential equationsNIM is simple in its principles and easy to implement on computer packages such as Mathematica and Maple. This method is better than numerical methods as it is free from rounding off errors and does not require large computer power. NIM has proven successful over other methods in many cases [17], [18] [19], [20] [21], [22], [16].Bhaleker, S. and Datterder-Gejj, V. [18] presented a modification of the NIM called the Revised NIM (RNIM), to solve the following system of functional equations with improved convergence: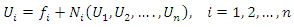 | (4) |
2. Description of the Methods
2.1. New Iterative Method
- Consider the system of nonlinear functional equations in equation (4) above, where
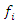 are known functions and
are known functions and 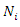 are nonlinear operators. Let
are nonlinear operators. Let 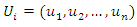 be a solution of system (4), where
be a solution of system (4), where 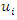 having the series form:
having the series form: | (5) |
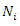 can be decompose as
can be decompose as 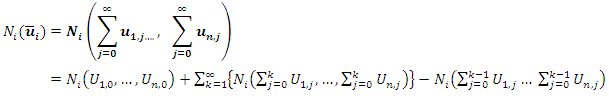 | (6) |
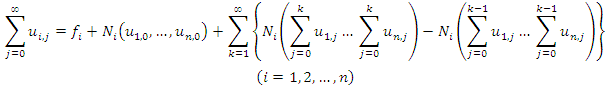 for
for  we define the recurrence relation:
we define the recurrence relation: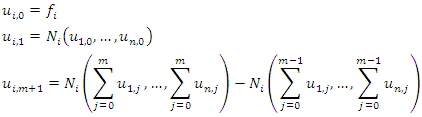 then
then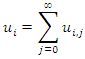 The
The 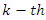 order approximation of
order approximation of 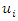 is given by
is given by 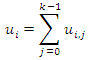
2.2. Revised New Iterative Method
- In this section we present the algorithm of the RNIM suggested by [18] to illustrate the technique. We consider the system of equation (4).Initial step
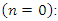
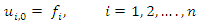 First Iteration
First Iteration 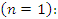
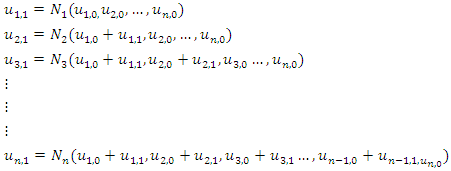 kth Iteration
kth Iteration 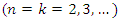
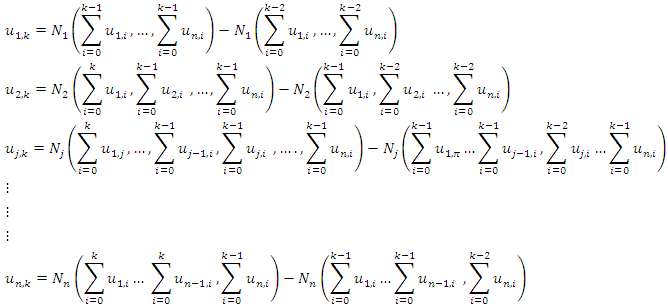 Thus
Thus 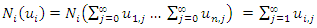 Hence,
Hence, 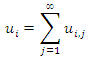
3. Revised NIM for the System (1) - (3)
- In view of the RNIM, the system (1) - (3) is equivalent to the system of Integral equation:
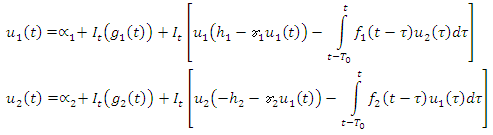 where
where 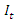 is an integral operator with respect to
is an integral operator with respect to  We set
We set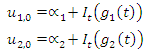 Therefore,
Therefore,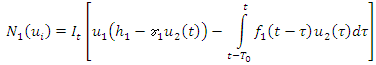 and
and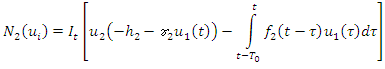 Now for n=1, we get
Now for n=1, we get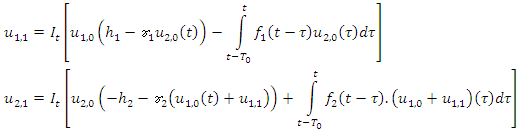 Second iteration: n=2 gives;
Second iteration: n=2 gives;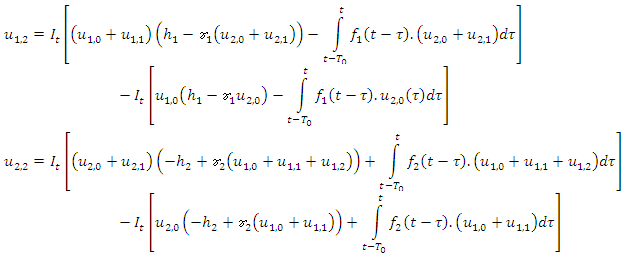 Third Iteration: n=3 results to;
Third Iteration: n=3 results to;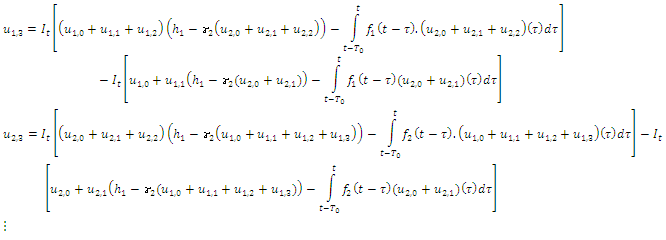 and so on. The rest iterations can be obtained.The solution is of the form
and so on. The rest iterations can be obtained.The solution is of the form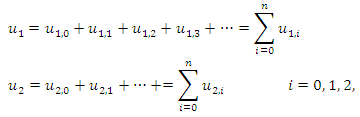
4. Illustrative Examples
- To give a clear over view of this method, we present the following examples. We apply the revised NIM and compare the results with the other numerical methods. Results are shown with tables and figures below. All of them were performed on the computer using a program written in Maple 15.Example 4.1. [13]: Consider the system of Integro-differential equation (1) and (2) with
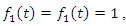
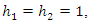
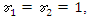
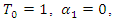
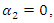
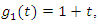 and
and 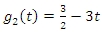 with the exact solution as
with the exact solution as 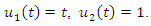 By solving the system (1) – (2) using the RNIM algorithm with this data, we obtain approximate solution as
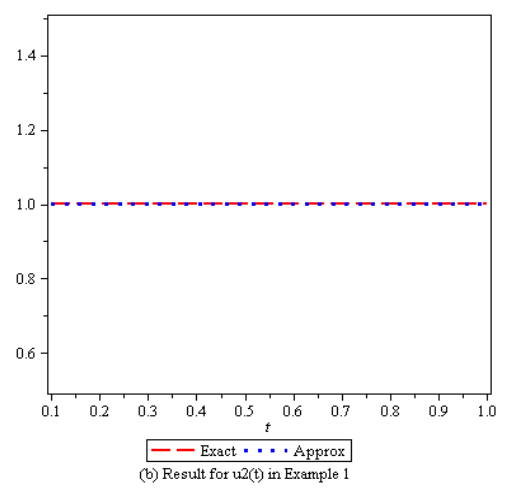
By solving the system (1) – (2) using the RNIM algorithm with this data, we obtain approximate solution as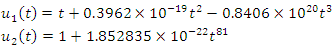 This is indeed the exact solution of the problem.In figure (1) and (2), approximate and exact solutions are plotted.
This is indeed the exact solution of the problem.In figure (1) and (2), approximate and exact solutions are plotted.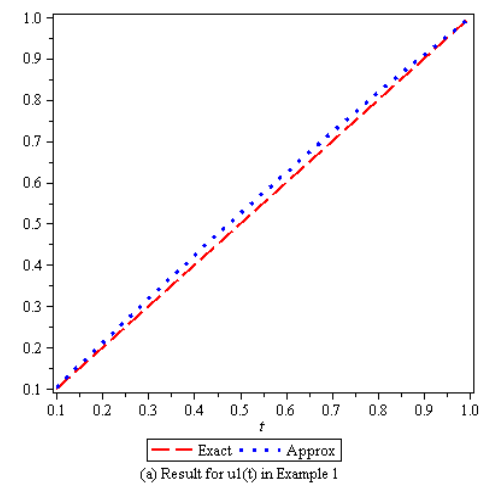 | Figure 1. |
 | Figure 2. |
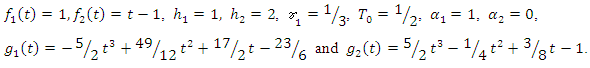 The exact solutions of this system are in the form
The exact solutions of this system are in the form We obtain the approximate solutions by RNIM and get
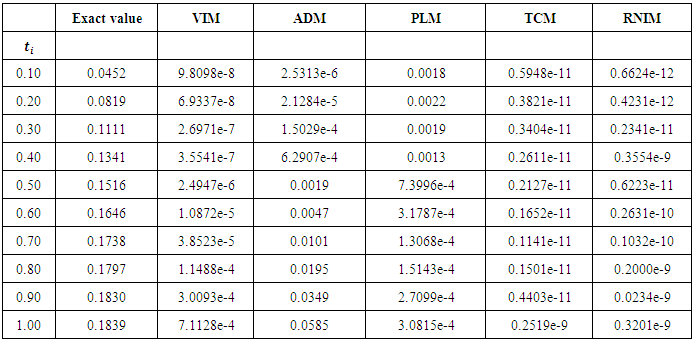
We obtain the approximate solutions by RNIM and get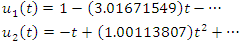 These results show the high accuracy of the technique only by two Iterations.In Table 1 – 2, the absolute errors obtained by the RNIM are compared with the results obtained by variational Iteration method [10], Taylor collocation method [13], Adomian decomposition method [9] and Pseudospectral Legendre method [11]. In figure 3 – 4, the exact and approximate value for
These results show the high accuracy of the technique only by two Iterations.In Table 1 – 2, the absolute errors obtained by the RNIM are compared with the results obtained by variational Iteration method [10], Taylor collocation method [13], Adomian decomposition method [9] and Pseudospectral Legendre method [11]. In figure 3 – 4, the exact and approximate value for 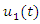 and
and  is plotted. It is seen from this figure and tables that the present method is closer to exact solution than other method.
is plotted. It is seen from this figure and tables that the present method is closer to exact solution than other method.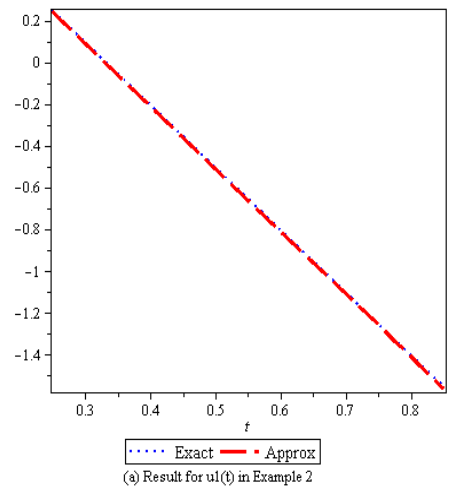 | Figure 3. |
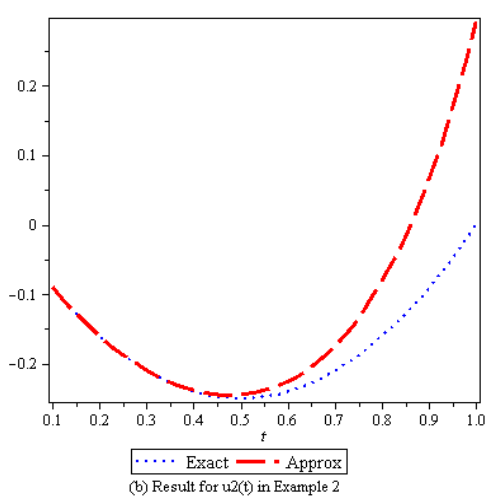 | Figure 4. |
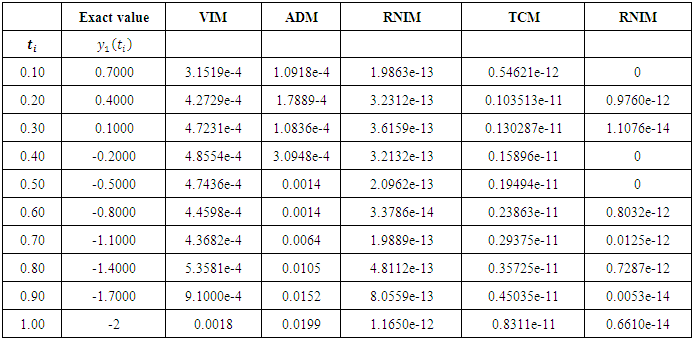 | Table 1. Comparison of the absolute errors obtained by the ADM, PLM, TCM, VIM and the RNIM for 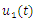 in Example 2 in Example 2 |
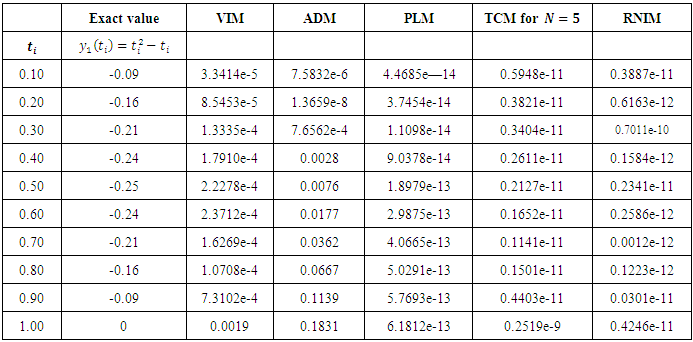 | Table 2. Comparison of the absolute errors obtained by the ADM, PLM, TCM, VIM and the RNIM for 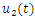 in Example 2 in Example 2 |
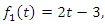
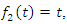
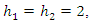
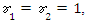
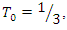
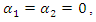
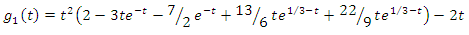 and
and 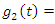
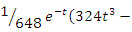
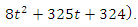 The exact solution of this system is in the form
The exact solution of this system is in the form 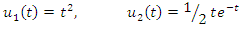 Using the RNIM algorithm, we calculate the approximate solutions
Using the RNIM algorithm, we calculate the approximate solutions 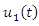 and
and 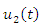 and get
and get 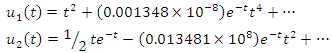 The exact solutions, absolute errors obtained by other methods and the present method are given in table 3 – 4.
The exact solutions, absolute errors obtained by other methods and the present method are given in table 3 – 4.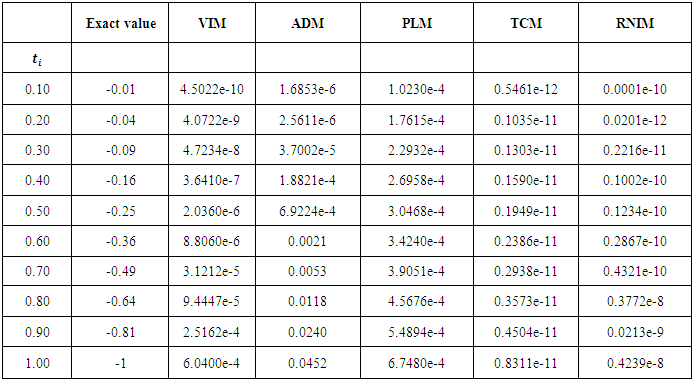 | Table 3. Comparison of the absolute errors obtained by the ADM, PLM, TCM, VIM and the RNIM for  in Example 3 in Example 3 |
 | Table 4. Comparison of the absolute errors obtained by the ADM, PLM, TCM, VIM and the RNIM for 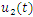 in Example 3 in Example 3 |
5. Conclusions
- In this present paper, we employed the modification of NIM; termed as “revised NIM” for solving a system of nonlinear delay Integro-differential equations which arises in a model describing biological species living together. The method yields a series solution which converges faster than numerical methods. It is then observed from figures and tables that the method is simple and powerful tool to obtain the approximate solution of this system.Maple 15 was used to carried out the computations.
6. Recommendations
- This method can also be extended to other models in future.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML