Sachin Bhalekar, Jayvant Patade
Department of Mathematics, Shivaji University, Kolhapur, India
Correspondence to: Sachin Bhalekar, Department of Mathematics, Shivaji University, Kolhapur, India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Fisher’s equation is very useful in modeling phenomena in neurophysiology, population dynamics and chemical kinetics. In this paper, a solution of this equation is obtained by utilizing Daftardar-Gejji and Jafari method (DJM). The comparison of our solution with the exact solution and those obtained by Adomian decomposition method (ADM) shows that the DJM is more accurate than ADM.
Keywords:
Fisher's equation, Daftardar-Gejji and Jafari method, Adomian decomposition method
Cite this paper: Sachin Bhalekar, Jayvant Patade, An Analytical Solution of Fisher’s Equation Using Decomposition Method, American Journal of Computational and Applied Mathematics , Vol. 6 No. 3, 2016, pp. 123-127. doi: 10.5923/j.ajcam.20160603.01.
1. Introduction
Various natural systems are modeled by partial differential equations and most of them are nonlinear. However, solving such nonlinear equations is not easier, in general. Therfore, investigating different efficient methods to solve such equations is an important topic of research.In [1], Fisher introduced a partial differential equation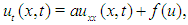 describing a mutation occuring in a population distrbuted in a linear habitat. A particular case of this equation
describing a mutation occuring in a population distrbuted in a linear habitat. A particular case of this equation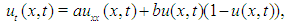 | (1) |
where 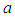 is the diffusion coefficient and
is the diffusion coefficient and 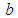 is the reactive factor is known as Fisher's equation. The nonlinear reaction-diffusion equations of this form are used to model various phenomena. Canosa [2, 3] used this equation to model the behavior of neutron population in a nuclear reactor. A similar equation was derived by Zeldowitsch and Frank- Kamenetzki [4] in the theory of thermal propagation of flame. The equation (1) also occurs in logistic population growth [5], autocatalytic chemical reactions [6] and Brownian motion [7].The Laurent series expantion was utilised by Ablowitz and Zepetella [8] to solve equation (1). Wang [9] used transformations
is the reactive factor is known as Fisher's equation. The nonlinear reaction-diffusion equations of this form are used to model various phenomena. Canosa [2, 3] used this equation to model the behavior of neutron population in a nuclear reactor. A similar equation was derived by Zeldowitsch and Frank- Kamenetzki [4] in the theory of thermal propagation of flame. The equation (1) also occurs in logistic population growth [5], autocatalytic chemical reactions [6] and Brownian motion [7].The Laurent series expantion was utilised by Ablowitz and Zepetella [8] to solve equation (1). Wang [9] used transformations 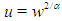 to derive solution of generlized Fisher's equation. Further, the solution was obtained by Hariharan et al. [10] by using Haar wavelet method. The traveling wave solution of equation (1) in two spatial dimensions was dicussed by Tyson and Brazhnik [11]. Tang and Weber [12] developed a numerical scheme to solve this equation. The Adomian decomposition method (ADM) was used to solve equation (1) in [13].A new iterative method was introduced by Daftardar-Gejji and Jafari (DJM) [14] in 2006 for solving functional equations. The DJM has been used to solve nonlinear equations such as fractional differential equations [15], partial differential equations [16], boundary value problems [17, 18], evolution equations [19], system of nonlinear functional equations [20] and so on. The method is successfully employed to solve Newell-Whitehead-Segel equation [21], fractional-order logistic equation [22] and some nonlinear dynamical systems [23] also. Recently DJM has been used to generate new numerical methods [24-26] for solving differential equations. The Adomian decomposition method (ADM) [27] introduced and developed by George Adomian is another useful method for solving nonlinear problems. The method is employed to solve nonlinear integro-differential equations in [28]. The reaction-convection-diffusion equation arising in chemistry was successfully solved using ADM in [29]. Wazwaz used ADM to solve boundary value problem [30], Kadomtsev-Petviashvili equation [31], partial differential equations [32] and diffusion equations [33]. Recently Jafari [34] used ADM and DJM to solve time–fractional Klein-Gordon type equation. The paper is organized as follows: The DJM and ADM are described briefly in Section 2. The convergence results for DJM are described in section 3. Application of DJM to solve Fisher’s equation is discussed in Section 4. Section 5 deals with different types of illustrative examples and conclusions are summarized in Section 6.
to derive solution of generlized Fisher's equation. Further, the solution was obtained by Hariharan et al. [10] by using Haar wavelet method. The traveling wave solution of equation (1) in two spatial dimensions was dicussed by Tyson and Brazhnik [11]. Tang and Weber [12] developed a numerical scheme to solve this equation. The Adomian decomposition method (ADM) was used to solve equation (1) in [13].A new iterative method was introduced by Daftardar-Gejji and Jafari (DJM) [14] in 2006 for solving functional equations. The DJM has been used to solve nonlinear equations such as fractional differential equations [15], partial differential equations [16], boundary value problems [17, 18], evolution equations [19], system of nonlinear functional equations [20] and so on. The method is successfully employed to solve Newell-Whitehead-Segel equation [21], fractional-order logistic equation [22] and some nonlinear dynamical systems [23] also. Recently DJM has been used to generate new numerical methods [24-26] for solving differential equations. The Adomian decomposition method (ADM) [27] introduced and developed by George Adomian is another useful method for solving nonlinear problems. The method is employed to solve nonlinear integro-differential equations in [28]. The reaction-convection-diffusion equation arising in chemistry was successfully solved using ADM in [29]. Wazwaz used ADM to solve boundary value problem [30], Kadomtsev-Petviashvili equation [31], partial differential equations [32] and diffusion equations [33]. Recently Jafari [34] used ADM and DJM to solve time–fractional Klein-Gordon type equation. The paper is organized as follows: The DJM and ADM are described briefly in Section 2. The convergence results for DJM are described in section 3. Application of DJM to solve Fisher’s equation is discussed in Section 4. Section 5 deals with different types of illustrative examples and conclusions are summarized in Section 6.
2. Methods
2.1. Daftardar-Gejji and Jafari Method
In this section we describe a Daftardar-Gejji and Jafari Method (DJM) [14], which is useful for solving the equations of the form 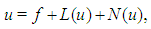 | (2) |
where 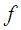 source term,
source term, 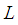 and
and 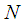 are linear and nonlinear operators respectively. Suppose
are linear and nonlinear operators respectively. Suppose 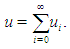 | (3) |
is the DJM solution for the Eq.(2).The nonlinear operator 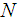 in Eq.(2) is decomposed as:
in Eq.(2) is decomposed as: 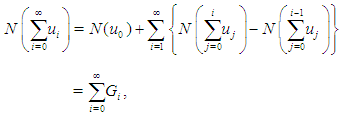 | (4) |
where 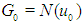 and
and 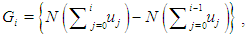
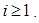 Since
Since 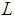 is linear, using equations (3) and (4) in Eq.(2), we get
is linear, using equations (3) and (4) in Eq.(2), we get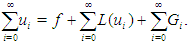 Thus, the DJM series terms are generated as below:
Thus, the DJM series terms are generated as below: 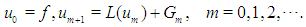 | (5) |
2.2. Adomian Decomposition Method
The ADM solution of equation (2) takes the same form as (3). The nonlinear operator 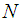 in equation (2) was decomposed by Adomian [27] as
in equation (2) was decomposed by Adomian [27] as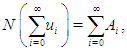 where
where 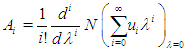 | (6) |
are called as Adomian polynomials.Equation (2) becomes 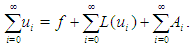 | (7) |
From Eq.(8), the ADM series terms are generated as bellow: 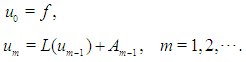 | (8) |
3. Convergence of DJM
The following convergence results for DJM are described by Daftardar-Gejji and Bhalekar [35]. Theorem 1. If 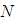 is
is 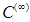 in a neighborhood of
in a neighborhood of 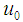 and
and 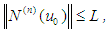 for any
for any 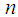 and for some real
and for some real 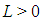 and
and 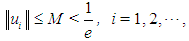 then the series
then the series 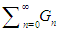 is absolutely convergent to
is absolutely convergent to 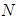 and moreover,
and moreover, 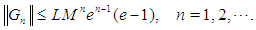 Theorem 2. If
Theorem 2. If 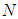 is
is 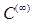 and
and 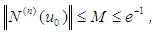
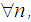 then the series
then the series 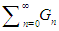 is absolutely convergent to
is absolutely convergent to 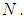
4. Applications
Eq.(1) with initial condition 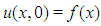 can be written equivalently as
can be written equivalently as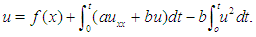 | (9) |
This Eq.(9) is of the form Eq.(2), with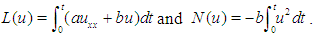 | (10) |
Using Eq.(5), the DJM series terms are generated as bellow: 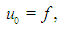 | (11) |
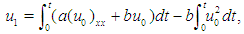 | (12) |
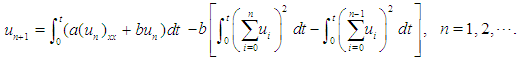 | (13) |
5. Illustrative Examples
Example 5.1 Consider the Fisher’s equation [13]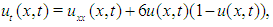 with
with 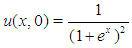 | (14) |
The equivalent integral equation is 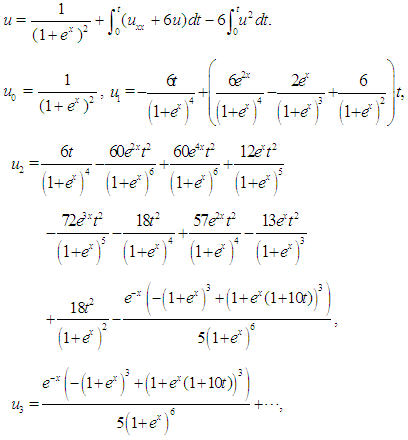 | (15) |
and so onThe four-term DJM approximate solution of Eq.(14) is 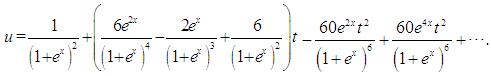 The exact solution of Eq.(14) is
The exact solution of Eq.(14) is 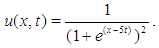 | (16) |
The four-term ADM approximate solution of Eq.(14) is described in [13] as 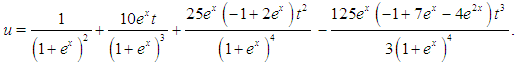 | (20) |
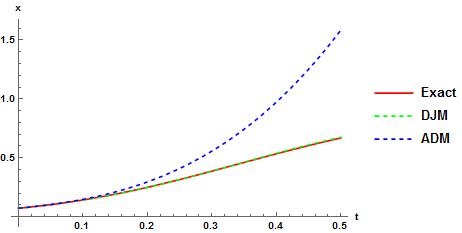
We compare 4-term DJM solution and ADM solution with exact solution in Fig.1 and Fig.2. It is observed that DJM solution is very well in agreement with exact solution.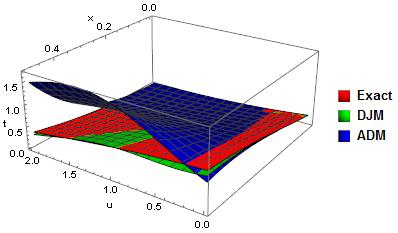 | Figure 1. Comparison of solutions of Eq.(14) |
 | Figure 2. Comparison for x = 1 |
Example 5.2 Consider the Fisher’s equation [13] 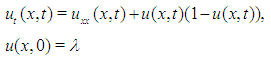 | (17) |
The equivalent integral equationis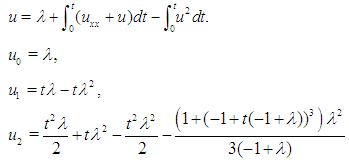 | (18) |
and so on.The Five-term DJM solution of Eq.(17) is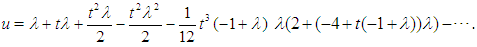 The exact solution of Eq.(17) is
The exact solution of Eq.(17) is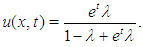 The Five-term ADM solution of Eq.(17) is described in [13] as
The Five-term ADM solution of Eq.(17) is described in [13] as 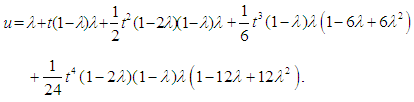 | (19) |
We compare these approximate solutions with exact solution in Fig.3 and Fig.4. It can be observed that DJM solution matches with exact solution.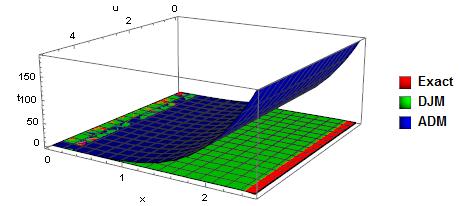 | Figure 3. Comparison of solutions of Eq.(17) |
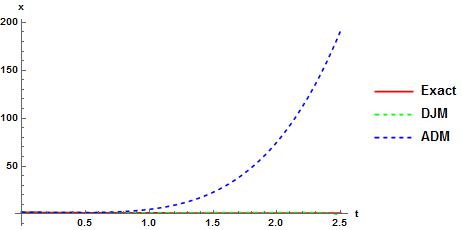 | Figure 4. Comparison for 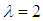 |
Example 5.3 Consider Fisher type nonlinear diffusion equation [13]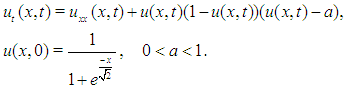 | (20) |
The equivalent integral equation is 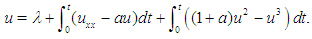 | (21) |
We compare 4-term DJM and ADM solutions [13] of Eq.(20) with exact solution in Fig.5 and Fig.6. It can be concluded that DJM solution is more accurate than ADM solution in this case also. 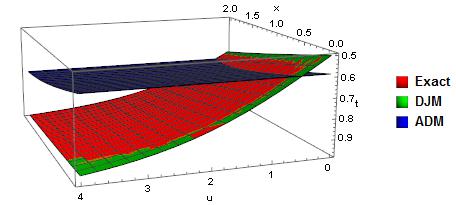 | Figure 5. Comparison of solutions of Eq.(20) |
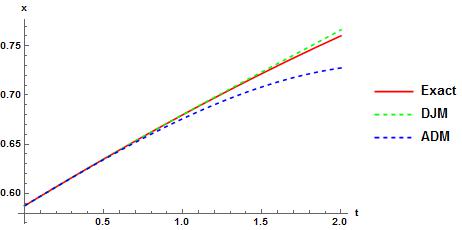 | Figure 6. Comparison for 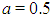 |
6. Conclusions
It is observed that Daftardar-Gejji and Jafari Method (DJM) is a simple but powerful technique used to solve Fisher's equations. The approximate solutions obtained using few series terms of DJM produce better results as compared with Adomian decomposition method.
ACKNOWLEDGEMENTS
The authors acknowledge NBHM, Department of Atomic Energy Mumbai, India for funding through Research Project [2148(6)/2013/NBHM(R.P.)/R & D II/689]. S. Bhalekar also acknowledges CSIR, New Delhi for funding through Research Project [25(0245)/15/EMR-II].
References
| [1] | R. A. Fisher, The wave of advance of advantageous genes. Annals of Eugenics. 7(4) (1937) 355–69. |
| [2] | J.Canosa, J. Math. Phys.10(10) (1969) 1868. |
| [3] | J. Canosa, IBM J. Res. Develop. 17 (1973) 13. |
| [4] | J. B. Zeldowitsch and D.A. Frank-Kamenetzki, Acta Physicochimica U.R.S.S. 9(2) (1938) 350. |
| [5] | J. D. Murray, Lectures on nonlinear differential equations models in biology, Oxford University Press, London, 1977. |
| [6] | P. C.Fife and J.B. McLeod, Arch. Rational Mech. Anal. 65 (1977) 361. |
| [7] | M.D. Bramson, Comm. Pure Appl. Math. 31 (1978) 581. |
| [8] | M. Ablowitz and A. Zepetella, Bull. Math. Biol. 41 (1979) 840. |
| [9] | X.Y. Wang, Phys. Lett. A 131(4/5) (1988) 279. |
| [10] | G. Hariharan, K. Kannan and K. R. Sharma. Appl. Math. Comput. 211(2) (2009) 92. |
| [11] | J. J. Tyson and P. K. Brazhnik, SIAM Journal on Applied Mathematics. 60(2) (2000) 391. |
| [12] | S. Tang and R. O. Weber. The Journal of the Australian Mathematical Society. Series B. Applied Mathematics. 33(01) (1991) 38. |
| [13] | A.M. Wazwaz, A. Gorguis, Appl. Math. Comput. 154(3) (2004) 609. |
| [14] | V. Daftardar-Gejji and H. Jafari, J. Math. Anal. Appl. 316 (2006) 753. |
| [15] | V. Daftardar-Gejji and S. Bhalekar, Frac. Calc. Appl. Anal. 11 (2008) 193. |
| [16] | S. Bhalekar and V. Daftardar-Gejji, Appl. Math. Comput. 203 (2008) 778. |
| [17] | V. Daftardar-Gejji and S. Bhalekar, Comput. Math. Appl. 59 (2010) 1801. |
| [18] | S. T. Mohyud-Din, A. Yildirim and M. M. Hosseini, World Appl. Sci. J. 8 (2010) 531. |
| [19] | S. Bhalekar and V. Daftardar-Gejji, Numer. Methods Partial Differential Equations, 26 (2010) 906. |
| [20] | S. Bhalekar and V. Daftardar-Gejji, Int. J. Computa. Math. Sci. 6 (2012) 127. |
| [21] | J. Patade and S. Bhalekar, World J. Modell. Simul. 11(2) (2015) 94. |
| [22] | S. Bhalekar and V. Daftardar-Gejji, Int. J. Differ. Equ. 2010 (2012) Art. ID 975829. |
| [23] | S. Bhalekar and V. Daftardar-Gejji, J. Appl. Nonlin. Dyn. 1 (2012) 141. |
| [24] | V. Daftardar-Gejji, Y. Sukale and S Bhalekar, Appl. Math. Comput. 244 (2014) 158. |
| [25] | V. Daftardar-Gejji, Y. Sukale and S Bhalekar, Fract. Calc. Appl. Anal. 16 (2015) 400. |
| [26] | J. Patade and S. Bhalekar, World J. Modell. Simul. 11 (2015) 256. |
| [27] | G. Adomian, Solving frontier problems of physics: The decomposition method, Kluwer, 1994. |
| [28] | G. Adomian and R. Rach, J. Math. Anal. Appl., 113(1) (1986) 199. |
| [29] | Y. Eugene, Appl. Math. Comput. 56 (1993) 1. |
| [30] | A. M. Wazwaz, J. Comput. Appl. Math. 136(1) (2001) 259. |
| [31] | A. M. Wazwaz, Appl. Math. Comput. 123(2) (2001) 205. |
| [32] | A. M. Wazwaz, Appl. Math. Comput. 123(2) (2001) 219. |
| [33] | A. M. Wazwaz, Appl. Math. Comput., 123(1) (2001) 109. |
| [34] | Hossein Jafari, J. Comput. Nonlinear Dyn. (2016). |
| [35] | S. Bhalekar and V. Daftardar-Gejji, Int. J. Differ. Equ. 2011 (2011). |



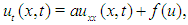 describing a mutation occuring in a population distrbuted in a linear habitat. A particular case of this equation
describing a mutation occuring in a population distrbuted in a linear habitat. A particular case of this equation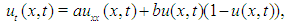
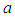 is the diffusion coefficient and
is the diffusion coefficient and 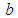 is the reactive factor is known as Fisher's equation. The nonlinear reaction-diffusion equations of this form are used to model various phenomena. Canosa [2, 3] used this equation to model the behavior of neutron population in a nuclear reactor. A similar equation was derived by Zeldowitsch and Frank- Kamenetzki [4] in the theory of thermal propagation of flame. The equation (1) also occurs in logistic population growth [5], autocatalytic chemical reactions [6] and Brownian motion [7].The Laurent series expantion was utilised by Ablowitz and Zepetella [8] to solve equation (1). Wang [9] used transformations
is the reactive factor is known as Fisher's equation. The nonlinear reaction-diffusion equations of this form are used to model various phenomena. Canosa [2, 3] used this equation to model the behavior of neutron population in a nuclear reactor. A similar equation was derived by Zeldowitsch and Frank- Kamenetzki [4] in the theory of thermal propagation of flame. The equation (1) also occurs in logistic population growth [5], autocatalytic chemical reactions [6] and Brownian motion [7].The Laurent series expantion was utilised by Ablowitz and Zepetella [8] to solve equation (1). Wang [9] used transformations 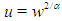 to derive solution of generlized Fisher's equation. Further, the solution was obtained by Hariharan et al. [10] by using Haar wavelet method. The traveling wave solution of equation (1) in two spatial dimensions was dicussed by Tyson and Brazhnik [11]. Tang and Weber [12] developed a numerical scheme to solve this equation. The Adomian decomposition method (ADM) was used to solve equation (1) in [13].A new iterative method was introduced by Daftardar-Gejji and Jafari (DJM) [14] in 2006 for solving functional equations. The DJM has been used to solve nonlinear equations such as fractional differential equations [15], partial differential equations [16], boundary value problems [17, 18], evolution equations [19], system of nonlinear functional equations [20] and so on. The method is successfully employed to solve Newell-Whitehead-Segel equation [21], fractional-order logistic equation [22] and some nonlinear dynamical systems [23] also. Recently DJM has been used to generate new numerical methods [24-26] for solving differential equations. The Adomian decomposition method (ADM) [27] introduced and developed by George Adomian is another useful method for solving nonlinear problems. The method is employed to solve nonlinear integro-differential equations in [28]. The reaction-convection-diffusion equation arising in chemistry was successfully solved using ADM in [29]. Wazwaz used ADM to solve boundary value problem [30], Kadomtsev-Petviashvili equation [31], partial differential equations [32] and diffusion equations [33]. Recently Jafari [34] used ADM and DJM to solve time–fractional Klein-Gordon type equation. The paper is organized as follows: The DJM and ADM are described briefly in Section 2. The convergence results for DJM are described in section 3. Application of DJM to solve Fisher’s equation is discussed in Section 4. Section 5 deals with different types of illustrative examples and conclusions are summarized in Section 6.
to derive solution of generlized Fisher's equation. Further, the solution was obtained by Hariharan et al. [10] by using Haar wavelet method. The traveling wave solution of equation (1) in two spatial dimensions was dicussed by Tyson and Brazhnik [11]. Tang and Weber [12] developed a numerical scheme to solve this equation. The Adomian decomposition method (ADM) was used to solve equation (1) in [13].A new iterative method was introduced by Daftardar-Gejji and Jafari (DJM) [14] in 2006 for solving functional equations. The DJM has been used to solve nonlinear equations such as fractional differential equations [15], partial differential equations [16], boundary value problems [17, 18], evolution equations [19], system of nonlinear functional equations [20] and so on. The method is successfully employed to solve Newell-Whitehead-Segel equation [21], fractional-order logistic equation [22] and some nonlinear dynamical systems [23] also. Recently DJM has been used to generate new numerical methods [24-26] for solving differential equations. The Adomian decomposition method (ADM) [27] introduced and developed by George Adomian is another useful method for solving nonlinear problems. The method is employed to solve nonlinear integro-differential equations in [28]. The reaction-convection-diffusion equation arising in chemistry was successfully solved using ADM in [29]. Wazwaz used ADM to solve boundary value problem [30], Kadomtsev-Petviashvili equation [31], partial differential equations [32] and diffusion equations [33]. Recently Jafari [34] used ADM and DJM to solve time–fractional Klein-Gordon type equation. The paper is organized as follows: The DJM and ADM are described briefly in Section 2. The convergence results for DJM are described in section 3. Application of DJM to solve Fisher’s equation is discussed in Section 4. Section 5 deals with different types of illustrative examples and conclusions are summarized in Section 6.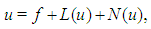
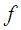 source term,
source term, 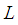 and
and 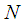 are linear and nonlinear operators respectively. Suppose
are linear and nonlinear operators respectively. Suppose 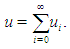
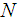 in Eq.(2) is decomposed as:
in Eq.(2) is decomposed as: 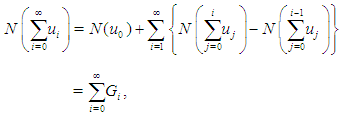
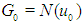 and
and 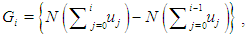
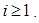 Since
Since 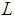 is linear, using equations (3) and (4) in Eq.(2), we get
is linear, using equations (3) and (4) in Eq.(2), we get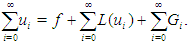 Thus, the DJM series terms are generated as below:
Thus, the DJM series terms are generated as below: 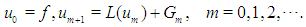
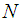 in equation (2) was decomposed by Adomian [27] as
in equation (2) was decomposed by Adomian [27] as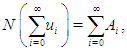 where
where 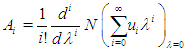
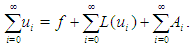
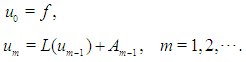
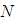 is
is 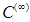 in a neighborhood of
in a neighborhood of 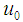 and
and 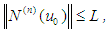 for any
for any 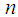 and for some real
and for some real 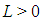 and
and 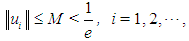 then the series
then the series 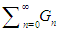 is absolutely convergent to
is absolutely convergent to 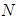 and moreover,
and moreover, 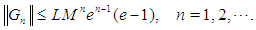 Theorem 2. If
Theorem 2. If 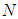 is
is 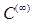 and
and 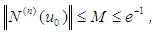
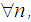 then the series
then the series 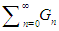 is absolutely convergent to
is absolutely convergent to 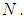
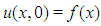 can be written equivalently as
can be written equivalently as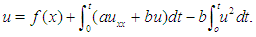
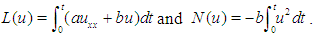
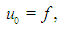
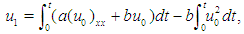
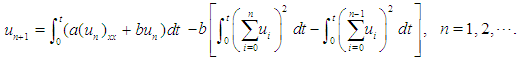
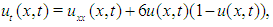 with
with 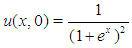
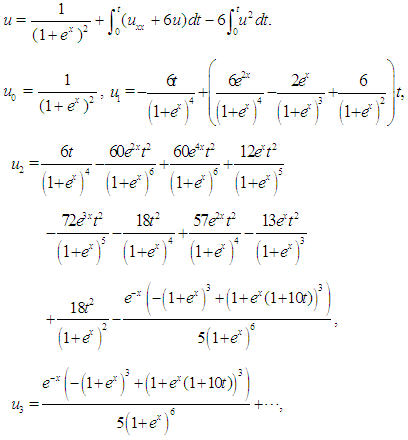
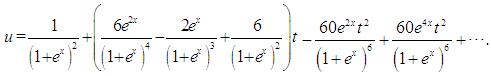 The exact solution of Eq.(14) is
The exact solution of Eq.(14) is 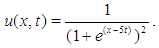
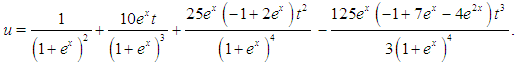


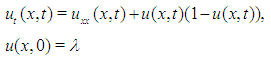
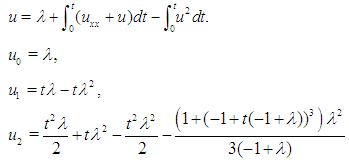
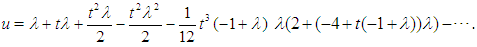 The exact solution of Eq.(17) is
The exact solution of Eq.(17) is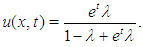 The Five-term ADM solution of Eq.(17) is described in [13] as
The Five-term ADM solution of Eq.(17) is described in [13] as 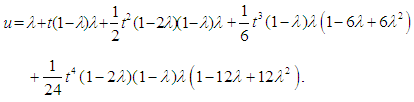


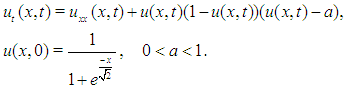
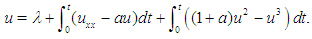


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML