-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(2): 118-122
doi:10.5923/j.ajcam.20160602.12

Comparative Notes on Banach Principle for Semifinite von Neumann Algebras (W* - Algebras) and JW-Algebras
Bassi I. G., Habu P. N., H. Ibrahim
Department of Mathematics, Federal University Lafia, Lafia, Nigeria
Correspondence to: Bassi I. G., Department of Mathematics, Federal University Lafia, Lafia, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The objective of the paper is to give a comparative survey notes on non-commutative extension of the Banach Principle for 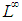 that was suggested in [3], [7], which extend the results in [8] to the case of JW-algebras without direct summand of the type
that was suggested in [3], [7], which extend the results in [8] to the case of JW-algebras without direct summand of the type 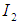 . We discuss relationships among the conditions
. We discuss relationships among the conditions 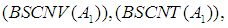 and
and 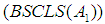 in JW-algebras as discussed in the case of the *-algebras. We introduced the notion of uniform equicontinuity for sequences of functions with values in the space of measurable operators and present a non – commutative version of the Banach Principle for
in JW-algebras as discussed in the case of the *-algebras. We introduced the notion of uniform equicontinuity for sequences of functions with values in the space of measurable operators and present a non – commutative version of the Banach Principle for 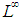 . We established the Banach Principle for semi-finite
. We established the Banach Principle for semi-finite 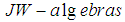 without direct summand of type I2, which was the extension of the results of Chilin and Litvinov on the Banach Principle for semi-finite von Neumann algebras. The results in this paper has shown how Banach Principle for semi-finite Von Neumann (W*-algebras) algebras was extended to the case of
without direct summand of type I2, which was the extension of the results of Chilin and Litvinov on the Banach Principle for semi-finite von Neumann algebras. The results in this paper has shown how Banach Principle for semi-finite Von Neumann (W*-algebras) algebras was extended to the case of 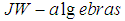 without direct summand of type I2.
without direct summand of type I2.
Keywords:
Von Neumann algebras, Measure topology, Jordan operator algebras, Almost uniform convergence, Banach Principle, *-algebra of 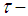 measurable operators affiliated to a semi-finite von Neumann algebra
measurable operators affiliated to a semi-finite von Neumann algebra
Cite this paper: Bassi I. G., Habu P. N., H. Ibrahim, Comparative Notes on Banach Principle for Semifinite von Neumann Algebras (W* - Algebras) and JW-Algebras, American Journal of Computational and Applied Mathematics , Vol. 6 No. 2, 2016, pp. 118-122. doi: 10.5923/j.ajcam.20160602.12.
Article Outline
1. Introduction
- Let
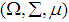 be a probability space. Denote by
be a probability space. Denote by 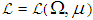 , the set of all (classes of) complex-valued measurable functions on
, the set of all (classes of) complex-valued measurable functions on 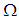 . Let
. Let 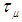 stand for the measure topology in . The classical Banach principle can be stated as follows:Classical Banach Principle. Let
stand for the measure topology in . The classical Banach principle can be stated as follows:Classical Banach Principle. Let 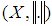 be a Banach space, and let
be a Banach space, and let 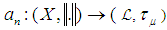 be a sequence of continuous linear maps. Consider the following properties:(i) the sequence
be a sequence of continuous linear maps. Consider the following properties:(i) the sequence 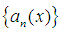 converges almost everywhere (a.e) for every
converges almost everywhere (a.e) for every 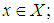 (ii)
(ii) 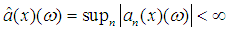 a.e for every
a.e for every 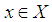 ;(iii) holds, and the maximal operator
;(iii) holds, and the maximal operator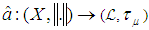 is continuous at 0;(iv) the set
is continuous at 0;(iv) the set 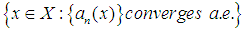 is closed in X.Then the implications
is closed in X.Then the implications 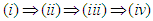 are always true. If in addition, there exists a dense subset
are always true. If in addition, there exists a dense subset 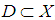 , such that the sequence
, such that the sequence 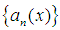 converges a.e. for every
converges a.e. for every 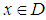 , then all the four conditions (i) – (iv) above are equivalent.The Banach Principle above was often applied in the case
, then all the four conditions (i) – (iv) above are equivalent.The Banach Principle above was often applied in the case 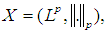 where
where 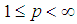 . However, in the case p =
. However, in the case p = 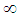 the uniform topology on
the uniform topology on 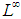 appears to be too strong for the classical Banach Principle to be effective in
appears to be too strong for the classical Banach Principle to be effective in 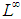 . For example, continuous functions are not uniformly dense
. For example, continuous functions are not uniformly dense 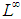 .Bellow and jones [3], using the fact that the unit ball
.Bellow and jones [3], using the fact that the unit ball 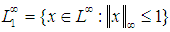 is complete in
is complete in 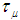 , suggested to consider the measure topology on
, suggested to consider the measure topology on 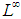 by replacing
by replacing 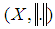 by
by 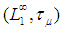 , since
, since 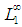 is not a linear space, however, some geometrical implications do occurred but was resolved by Bellow and Jones. A non-commutative version of the Banach Principle for
is not a linear space, however, some geometrical implications do occurred but was resolved by Bellow and Jones. A non-commutative version of the Banach Principle for 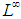 was proposed by Chilin and Litvinov, while the non-commutative notions of Banach Principle for measurable operators affiliated to a semi-finite von Neumann algebra (W*-algebra) were established by Goldstein, M; Litvinov, S and Litvinov, S; Mukhamedov, F. Then it was refined and applied in [5], [6], [13]. In [5] the notion of uniform equicontinuity of a sequence of functions into
was proposed by Chilin and Litvinov, while the non-commutative notions of Banach Principle for measurable operators affiliated to a semi-finite von Neumann algebra (W*-algebra) were established by Goldstein, M; Litvinov, S and Litvinov, S; Mukhamedov, F. Then it was refined and applied in [5], [6], [13]. In [5] the notion of uniform equicontinuity of a sequence of functions into 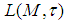 was introduced. The objective of the paper is to give a comparative survey notes on non-commutative extension of the Banach Principle for
was introduced. The objective of the paper is to give a comparative survey notes on non-commutative extension of the Banach Principle for 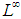 that was suggested in [3], [7], which extend the results in [8] to the case of JW-algebras without direct summand of the type
that was suggested in [3], [7], which extend the results in [8] to the case of JW-algebras without direct summand of the type 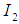 .
.2. Preliminaries
- Let
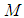 be a semi-finite von Neumann algebra of bounded operators acting on a complex Hilbert space
be a semi-finite von Neumann algebra of bounded operators acting on a complex Hilbert space 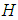 , and let
, and let 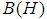 denote the algebra of all bounded linear operators on
denote the algebra of all bounded linear operators on 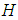 . A densely-defined closed operator
. A densely-defined closed operator 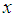 in
in 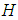 is said to be affiliated to
is said to be affiliated to 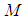 if
if 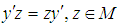 . We denote by
. We denote by 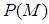 the complete lattice of projections in
the complete lattice of projections in 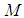 . Let
. Let 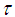 be a faithful normal semi-finite trace on
be a faithful normal semi-finite trace on 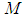 Denote by
Denote by 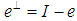 the orthogonal complemented projection for the projection
the orthogonal complemented projection for the projection 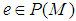 , where
, where 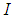 is the identity of
is the identity of 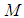 . An operator
. An operator 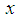 affiliated to
affiliated to 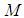 is called
is called 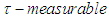 if for every
if for every 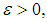 there exist a projection
there exist a projection 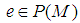 with
with 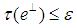 such that
such that 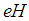 belongs to the domain of the operator
belongs to the domain of the operator  . Let
. Let 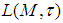 the set of all
the set of all 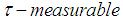 operator affiliated to
operator affiliated to 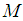 . Denote
. Denote 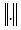 the uniform norm in
the uniform norm in 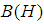 .If we set
.If we set 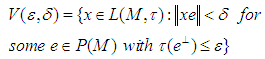 then, the topology
then, the topology 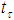 defined on
defined on 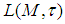 by the family
by the family 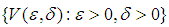 of neighborhoods of zero is called the measure topology ([14], [15])Theorem 1:
of neighborhoods of zero is called the measure topology ([14], [15])Theorem 1: 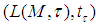 is a complete metrizable topological *-algebraProof: see ([14], [15]) for the details of the proof.Let
is a complete metrizable topological *-algebraProof: see ([14], [15]) for the details of the proof.Let 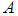 be a semifinite
be a semifinite 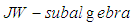 of
of 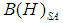 without a direct summand of type
without a direct summand of type 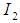 and
and 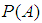 be the complete lattice of projections in
be the complete lattice of projections in 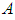 , and
, and 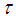 be a faithful normal semifinite trace on
be a faithful normal semifinite trace on 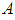 . Let
. Let 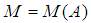 be the von Neumann enveloping algebra of the Jordan algebra
be the von Neumann enveloping algebra of the Jordan algebra 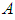 . Then
. Then 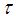 can be uniquely extended to a faithful normal semifinite trace on
can be uniquely extended to a faithful normal semifinite trace on 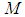 , for which we will use the same symbol
, for which we will use the same symbol 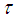 . A self adjoint operator
. A self adjoint operator 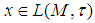 is called affiliated to a
is called affiliated to a 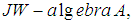 if all its spectral projections belong to
if all its spectral projections belong to 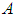 . An operator
. An operator 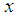 affiliated to
affiliated to 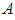 is called
is called 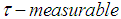 if for all
if for all 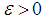 there exist
there exist 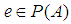 with
with 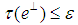 such that
such that 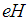 belongs to the domain of the operator
belongs to the domain of the operator 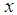 . Let
. Let 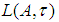 be the set of all
be the set of all 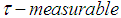 operators affiliated to
operators affiliated to 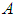 .Remark: A sequence
.Remark: A sequence 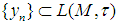 is said to converge almost uniformly (a.u) to
is said to converge almost uniformly (a.u) to 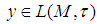 if for all
if for all 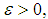 there exist
there exist 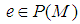 with
with 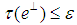 such that
such that 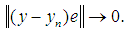 Proposition 1: For
Proposition 1: For 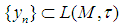 the following conditions are equivalent(i)
the following conditions are equivalent(i) 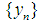 converges a.u. in
converges a.u. in 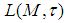 ;(ii) For all
;(ii) For all 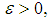 there exist
there exist 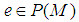 with
with 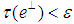 such that
such that 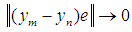 as
as 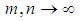 Proof: see [7] for detailsThe following theorem is a non-commutative notion of Riesz theorem. Theorem 2: If
Proof: see [7] for detailsThe following theorem is a non-commutative notion of Riesz theorem. Theorem 2: If 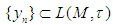 and
and 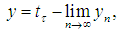 then
then 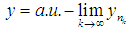 for some subsequence
for some subsequence 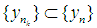 The proof of this theorem can be seen in [9] and [15].A sequence
The proof of this theorem can be seen in [9] and [15].A sequence 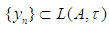 is said to converge bilaterally with square almost uniformly (b.s.a.u.) to
is said to converge bilaterally with square almost uniformly (b.s.a.u.) to 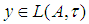 if given
if given 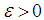 there is
there is 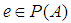 with
with 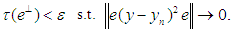 Then the following proposition holds;Proposition 2: For
Then the following proposition holds;Proposition 2: For 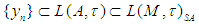 the following conditions are equivalent.(i)
the following conditions are equivalent.(i) 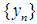 converges a.u. in
converges a.u. in 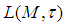 ;(ii) Given
;(ii) Given 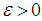 , there is
, there is 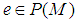 with
with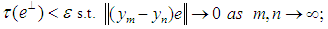 (iii)
(iii) 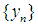 converges b.s.a.u.in
converges b.s.a.u.in 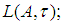 (iv) Given
(iv) Given 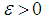 , there is
, there is 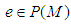 with
with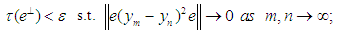 Proof: conditions (i)
Proof: conditions (i) 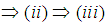 are trivial. For (iv) : From
are trivial. For (iv) : From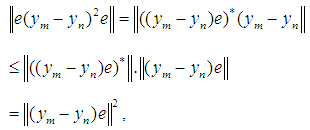 so we can see that b.s.a.u. fundamentalness of a sequence in a reversible JW-algebra is equivalent to a.u. fundamentalness of the same sequence in its von Neumann enveloping algebra M = M(A). Thus the statement follows from proposition 1 above and hence the proved. The Riesz theorem above will now take the following formTheorem 3: If
so we can see that b.s.a.u. fundamentalness of a sequence in a reversible JW-algebra is equivalent to a.u. fundamentalness of the same sequence in its von Neumann enveloping algebra M = M(A). Thus the statement follows from proposition 1 above and hence the proved. The Riesz theorem above will now take the following formTheorem 3: If 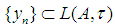 and
and 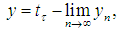 then
then 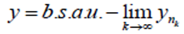 for some subsequence
for some subsequence 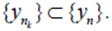 Proof: Directly from propositions 1 and 2 respectively.
Proof: Directly from propositions 1 and 2 respectively.3. Uniform Equicontinuity for Sequences of Maps into 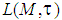
- Let E be any set. If
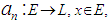 and
and 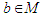 are such that
are such that 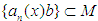 , then we denote
, then we denote 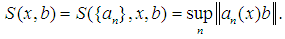 The following fact should be noted.Corollary: Let
The following fact should be noted.Corollary: Let 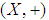 be a semigroup,
be a semigroup, 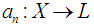 be sequence of additive maps. Assume that
be sequence of additive maps. Assume that 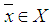 is such that for every
is such that for every 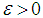 there exist a sequence
there exist a sequence 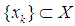 and a projection
and a projection 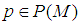 with
with 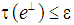 such that (i)
such that (i) 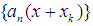 converges a.u. as
converges a.u. as 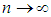 for every k;(ii)
for every k;(ii) 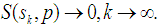 Then the sequence
Then the sequence 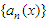 converges a.u. in L.Proof: Fix
converges a.u. in L.Proof: Fix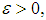 and let
and let 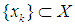 and
and 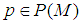 with
with 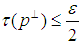 be such that the two conditions hold. Now pick
be such that the two conditions hold. Now pick 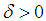 and let
and let 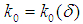 be such that
be such that 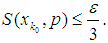 then by proposition 1, there is a projection
then by proposition 1, there is a projection 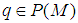 with
with 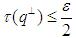 and a positive integer
and a positive integer 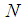 for which the inequality
for which the inequality 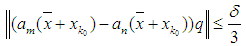 holds whenever
holds whenever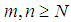 . If we define
. If we define 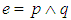 , then
, then 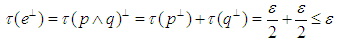 and
and 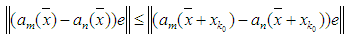
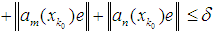 for all
for all 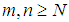 . Therefore by proposition 1, the sequence
. Therefore by proposition 1, the sequence 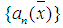 converges a.u. in L. The following definitions hold: Definition: A sequence
converges a.u. in L. The following definitions hold: Definition: A sequence 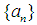 is said to be equicontinuous at
is said to be equicontinuous at 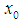 if, given
if, given 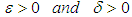 , there is a neighborhood U of
, there is a neighborhood U of 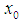 in (X,t) such that
in (X,t) such that 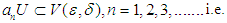 for every
for every 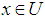 and every
and every 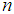 one can find a projection
one can find a projection 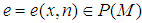 with
with 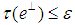 satisfying
satisfying 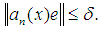 Now let
Now let 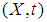 be a topological space, and let
be a topological space, and let 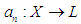 and
and 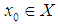 be such that
be such that 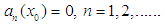 Definition: Let
Definition: Let 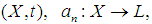 and
and 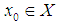 be as above. Let
be as above. Let 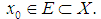 The sequence
The sequence 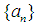 will be called uniformly equicontinuous at
will be called uniformly equicontinuous at 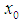 on E if, given
on E if, given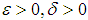 , there is a neighborhood U of
, there is a neighborhood U of 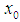 in
in 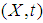 such that for every
such that for every 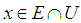 there exists a projection
there exists a projection 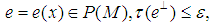 satisfying
satisfying 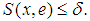
4. Bilateral with Square Uniform Equicontinuity for Sequences of Maps into 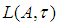
- Definition: Let
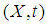 be a topological space,
be a topological space, 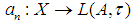 and
and 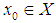 be such that
be such that 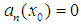 for
for 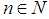 . A sequence
. A sequence 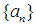 is called bilaterally with square equicontinuous at
is called bilaterally with square equicontinuous at 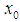 in
in 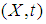 such that
such that 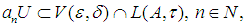 i.e. for all
i.e. for all 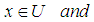 for all
for all 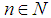 one can find a projection
one can find a projection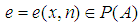 with
with 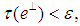 satisfying
satisfying 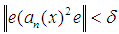 .Definition: Let
.Definition: Let 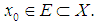 A sequence
A sequence 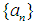 is called bilaterally with square uniformly equicontinuous at
is called bilaterally with square uniformly equicontinuous at 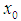 on E, if for all
on E, if for all 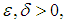 there is a neighborhood of
there is a neighborhood of 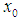 in
in 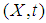 such that
such that 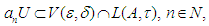 i.e. for all
i.e. for all 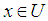 and for all
and for all 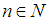 one can find a projection
one can find a projection 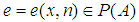 with
with 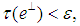 satisfying
satisfying 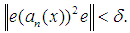 We can now define a bilaterally sequence with square uniformly equicontinuous as follows:Definition: Let
We can now define a bilaterally sequence with square uniformly equicontinuous as follows:Definition: Let 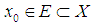 . A sequence
. A sequence 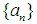 is called bilaterally with square uniformly equicontinuous at
is called bilaterally with square uniformly equicontinuous at 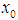 on E, if for all
on E, if for all 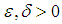 there is a neighborhood U of
there is a neighborhood U of 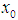 in
in 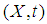 such that for all
such that for all 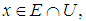 there is
there is 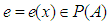 with
with 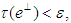 satisfying
satisfying 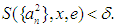 We then have the following resultProposition 3: Let the sequence
We then have the following resultProposition 3: Let the sequence 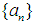 and
and 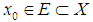 as in definition above. Then,(i)
as in definition above. Then,(i) 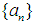 is equicontinuous at
is equicontinuous at 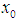 on E into
on E into 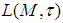 iff it is bilaterally with square equicontinuous at
iff it is bilaterally with square equicontinuous at 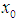 on E into
on E into 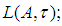 (ii)
(ii) 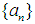 is uniformly equicontinuous at
is uniformly equicontinuous at 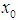 on E into
on E into 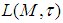 iff it is bilaterally with square uniformly equicontinuous at
iff it is bilaterally with square uniformly equicontinuous at 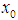 on E into
on E into 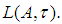 Proof: Directly follows from proposition 2 and arguments in [7]Also in [7] it has been established that for any
Proof: Directly follows from proposition 2 and arguments in [7]Also in [7] it has been established that for any 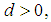 the sets
the sets 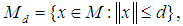 and
and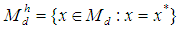 are
are 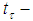 complete.Therefore,
complete.Therefore, 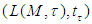 is a complete metrizable topological
is a complete metrizable topological 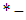 algebra, and
algebra, and 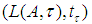 is a complete metrizable topological Jordan subalgebra of
is a complete metrizable topological Jordan subalgebra of 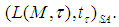 Hence, it is easy to see that the set
Hence, it is easy to see that the set 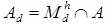 is
is 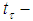 complete as well.
complete as well.5. Main Results
- In the
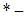 algebra, let’s consider the following conditions. Let
algebra, let’s consider the following conditions. Let 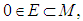 now for a sequence of function
now for a sequence of function 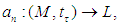 then(i)almost uniform convergence of
then(i)almost uniform convergence of 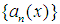 for every
for every 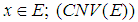 (ii) uniform equicontinuity at 0 on
(ii) uniform equicontinuity at 0 on 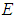 ;
;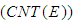 (iii) closedness in
(iii) closedness in 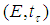 of the set
of the set 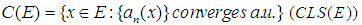 With these conditions, one can study relationships among the conditions
With these conditions, one can study relationships among the conditions 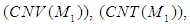 and
and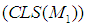 . Following the classical scheme, one more condition can be added, namely, a non-commutative version of the existence of the maximal operator as follows: given
. Following the classical scheme, one more condition can be added, namely, a non-commutative version of the existence of the maximal operator as follows: given 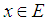 and
and 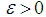 there is
there is 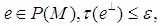 with
with 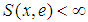 .
.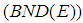 . This condition may be called a pointwise uniform boundedness of
. This condition may be called a pointwise uniform boundedness of 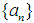 on . It can be easily verified that
on . It can be easily verified that 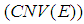 implies
implies 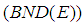 , but
, but 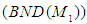 does not guarantee
does not guarantee 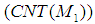 . However, if
. However, if 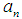 is additive for every
is additive for every 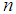 , then
, then 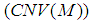 follows from
follows from 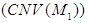 while if
while if 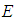 is closed in
is closed in 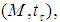 then
then 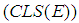 is equivalent to the closedness of
is equivalent to the closedness of 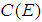 in
in 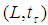 .In the JW-algebras, the above conditions can also be extended as follows: Let
.In the JW-algebras, the above conditions can also be extended as follows: Let 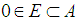 . For a sequence
. For a sequence 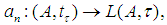 then(i) Bilateral with square almost uniform convergence of
then(i) Bilateral with square almost uniform convergence of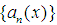 for every
for every 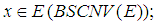 (ii) Bilateral with square uniform equicontinuity at 0 on
(ii) Bilateral with square uniform equicontinuity at 0 on 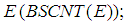 (iii) Closedness in
(iii) Closedness in 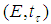 of the set
of the set 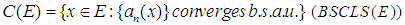 We can then discuss relationships among the conditions
We can then discuss relationships among the conditions 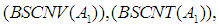 and
and 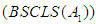 as discussed in the case of the *-algebras. These are summarized below in the following theorems and whose proofs are obtained directly in [7] and the arguments in this paper.Theorem 4: Let
as discussed in the case of the *-algebras. These are summarized below in the following theorems and whose proofs are obtained directly in [7] and the arguments in this paper.Theorem 4: Let 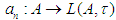 be a
be a 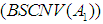 sequence of positive
sequence of positive 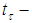 continuous linear maps with
continuous linear maps with 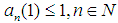 . Then the sequence
. Then the sequence 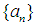 is also
is also 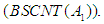 Theorem 5: A
Theorem 5: A 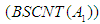 sequence of additive maps
sequence of additive maps 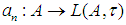 is as well
is as well 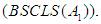 Theorem 6: Let
Theorem 6: Let 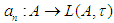 be a sequence of positive
be a sequence of positive 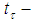 continuous linear maps such that
continuous linear maps such that 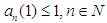 . If a sequence
. If a sequence 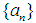 is
is 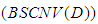
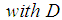 being
being 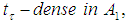 the conditions
the conditions 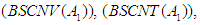
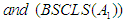 are equivalent.
are equivalent.6. Conclusions
- The results in this paper has shown how Banach Principle for semifinite Von Neumann (W*-algebras) algebras was extended to the case of
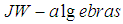 without direct summand of type I2. We can extend these results to the case of bilateral almost uniform convergence on semifinite von Neumann algebras and semifinite
without direct summand of type I2. We can extend these results to the case of bilateral almost uniform convergence on semifinite von Neumann algebras and semifinite 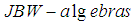 without direct summand of type I2. These results can further be extended to obtain Stochastic Banach Principle, and then apply it to obtain some new Ergodic type theorems for Jordan algebras.
without direct summand of type I2. These results can further be extended to obtain Stochastic Banach Principle, and then apply it to obtain some new Ergodic type theorems for Jordan algebras. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML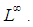 (English), Adv. Math., Vol. 36, 1996 155 – 172.
(English), Adv. Math., Vol. 36, 1996 155 – 172. measurable operators (English) Studia Math., Vol. 143, 2000, 33 – 41.
measurable operators (English) Studia Math., Vol. 143, 2000, 33 – 41.