1. Introduction

The analytical and numerical solutions of fractional differential equations (FDEs) attracted great attention and became a considerably interesting subject in mathematical physics. There are many methods for calculating the approximate solutions of FDEs such that the variational iterations method [1-5], Adomian decomposition method [6, 7] the homotopy perturbation method [8, 11] and the expansion-function method. [12-14]. The analytical solutions of FDEs are still of great interest. Li and He [15] introduced complex transform for reducing FDEs into ordinary differential equations (ODEs) [16, 17], so that all analytical methods for advanced calculus can be easily applied to fractional calculus. In the literature, there are many effective methods to treat analytical solutions of FDEs examples include the exponential function method, the fractional sub-equation method, the 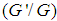-expansion method and the first integral method [18- 34].

The investigation of multi-wave solutions of the nonlinear partial differential equations (NLPDEs) and nonlinear FDEs plays an important role in the study of the corresponding physical phenomena. Zhang and Zhang [35] generalized the exp-function method for constructing multi-wave solutions of nonlinear differential difference equations by devising a rational ansätz of multiple exponential functions. Many authors [36-41] used the exp-function method to construct abundant types of exact solutions of PDEs. In [42] Abdel-Salam and Hassan improved generalized exp-function, also derived Multi-wave solutions of the space–time fractional Burgers and Sharma–Tasso–Olver equations. In this paper, the hierarchy of the space-time fractional (2+1) Burgers equation derived and the generalized exp-function method are used to obtain multi-wave solution of FDEs in a unified way. In addition, the single-kink wave, double-kink wave, three- kink wave, and four-kink wave solutions obtained for the (2+1) space-time fractional Burgers equation, the (2+1) space-time fractional Sharma–Tasso–Olver equation, the (2+1) space-time fractional fourth order Burgers equation and the (2+1) space-time fractional fifth order Burgers equation are studied.

The structure of this paper is as follows: some basic definitions of the fractional calculus and the description of the improved generalized exp-function method introduced in section 2. In section 3, the hierarchy of the integer order and fractional order of the (2+1) Burgers equation are investigated. In sections 4 -7, single- kink, double-kink, three-kink, and four-kink wave solutions are constructed for the (2+1) space-time fractional Burgers equation, the (2+1) space-time fractional Sharma–Tasso–Olver equation, the (2+1) space-time fractional fourth order Burgers equation and the (2+1) space-time fractional fifth order Burgers equation. In the last section, some conclusions are given.

2. Description of the Method

In this section we present the generalized exp-method to construct exact analytical solutions of nonlinear FDEs with the modified Riemann–Liouville derivative defined by Jumarie [43-50]

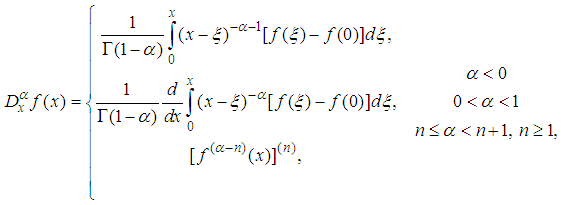(1)

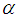which has merits over the original one, for example, the -order derivative of a constant is zero. Some properties of the Jumarie’s modified Riemann–Liouville derivative are

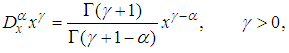(2)

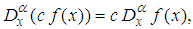(3)

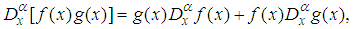(4)

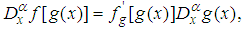(5)

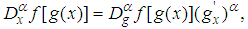(6)

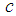where is constant. The formulas 4 - 6 follow from the fractional Leibniz rule and the fractional Barrow’s formula. That is direct results of the equality 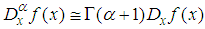, which holds for non-differentiable functions. We present the main steps of this method as follows:

Suppose that the nonlinear FDE, say in three variables 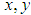and 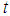, is given by:

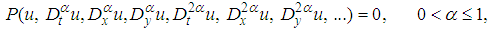(7)

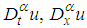where and 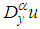are Jumarie’s modified Riemann–Liouville derivatives of 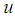, 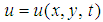is an unknown function, 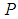is a polynomial in u and its various partial derivatives, other wise, a suitable transformation can transform equation (7) into such equation. The exp-function method for single-wave solution depend on the assumption that equation (7) has solution in the form

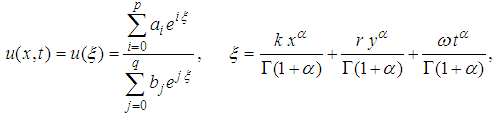(8)

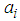where and 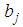are unknown constants to be determined, the value of 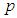and 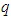can be determined by balancing the linear term of the highest order with the nonlinear term in equation (7).

In order to seek 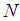-wave solution for arbitrary integer 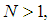we generalize equation (8) in the following form:

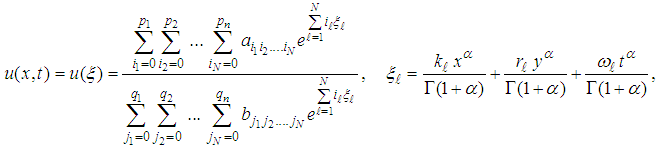(9)

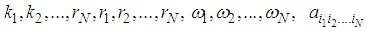where and 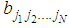are unknown constants to be determined later and 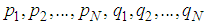are embedded integers.

When 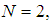equation (9) gives

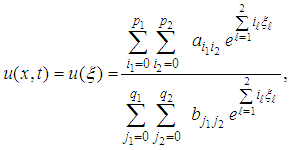(10)

which can be used to construct double-wave solution of equation (7).

When N = 3, equation (9) gives

(11)

which can be used to construct three-wave solution of equation (7).

Substituting equation (10) into the FDE (7), the left-hand side of equation (7) converted into a polynomial in exponential functions. Equating each coefficient of the exponential functions to zero gives system of algebraic equations. Solving the set of equations, we can obtain the double-wave solution. 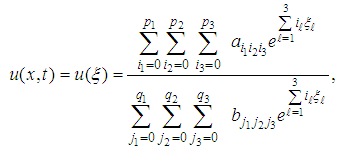In addition, we can obtain the three-wave and four- wave solutions by doing the same manner to equation (11).

3. Formulation of the (2+1) Space-Time Fractional Burgers Hierarchy

The space-time fractional Burgers hierarchy equation in (2+1)-dimension can be formulated as follows:

The Burgers hierarchy [51-54] in the (2+1)-dimension can be written in the form,

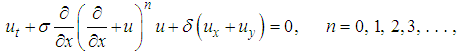(12)

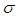where and 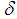are arbitrary constants. The first few elements of the hierarchy (12) are given by

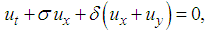(13)

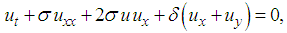(14)

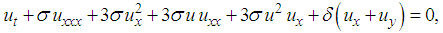(15)

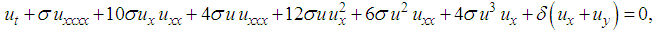(16)

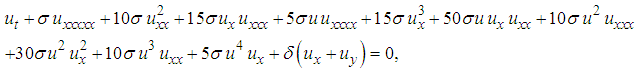(17)

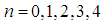obtained by substituting , respectively. The resulting PDEs are of first order, second order, third order, fourth order and fifth order (2+1)-Burgers equation, respectively. Equation (14) is the (2+1)-dimension Burgers equation. Moreover, equation (15) is the (2+1)-dimension Sharma–Tasso–Olver equation [52].

Similarly, the hierarchy of the (2+1) space-time fractional Burgers equation can be written in the form

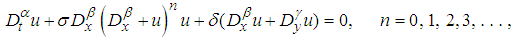(18)

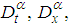where and 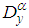are the fractional derivative of the modified Riemann–Liouville defined by equation (1). The first few elements of the space-time fractional hierarchy (18) are given by substituting 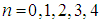, in equation (18), we have

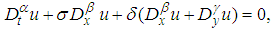(19)

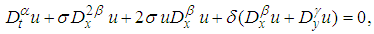(20)

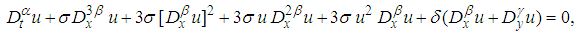(21)

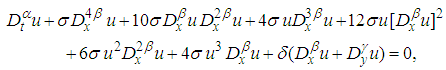(22)

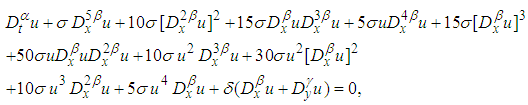(23)

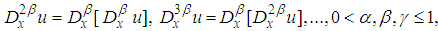where equations (19)- (23) are the first order, the second order, the third order, the fourth order and the fifth order (2+1)- space-time-fractional Burgers equation respectively.

4. The (2+1) Space-Time Fractional Burgers Equation

4.1. Single-Wave Solution

When 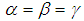, equation (20) becomes

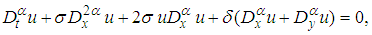(24)

which is called the space-time fractional (2+1) Burgers equation. For a single-wave solution, we assume that Equation (24) admits a solution of the form

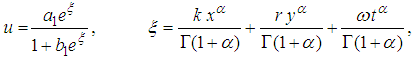(25)

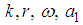where and 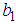are unknown constants to be determined. Based on the transformation above, for the terms in (24) containing fractional derivative, such as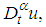 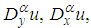and 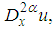using (3) and (5) one can obtain that

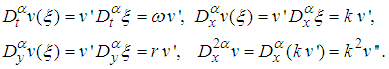(26)

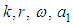Substituting (25) into equation (24) with (26), solving the resultant algebraic system for the unknowns and 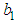, we obtain the solution set

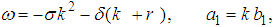(27)

which yields a single-wave solution to the (2+1) space-time fractional Burgers equation as

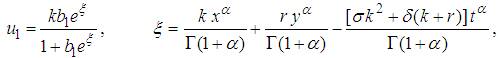(28)

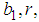where and 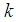are arbitrary constants. Equation (28) displays a single-kink wave solution of the (2+1) space-time fractional Burgers equation.

4.2. Double-Wave Solution

Suppose that equation (24) admits a solution of the form

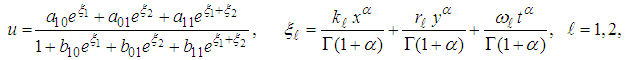(29)

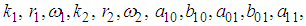where and 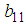are unknown constants to be determined. Substituting (29) into equation (24) with (26), solving the resultant algebraic system for the unknowns 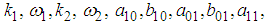and 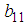, we obtain the solution set

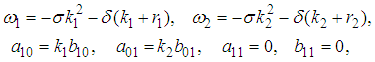(30)

which yields a double-wave solution to the (2+1) space-time fractional Burgers equation as

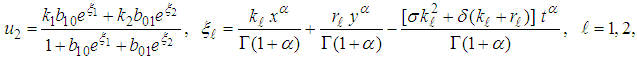(31)

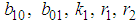where and 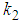are arbitrary constants. Equation (31) displays double-kink wave solution of the (2+1) space-time fractional Burgers equation.

4.3. Three-Wave Solution

Suppose that equation (24) admits a solution of the form

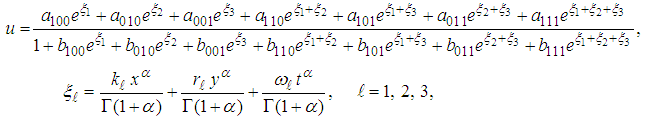(32)

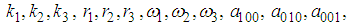
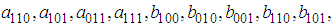
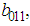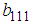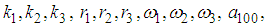
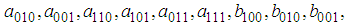
where and are unknown constants to be determined. Substituting (32) into equation (24) with (26), solving the resultant algebraic system for the unknowns 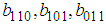and 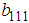, we obtain the solution set

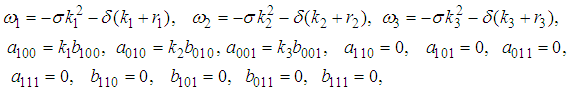(33)

which yields a three-wave solution to the (2+1) space-time fractional Burgers equation as

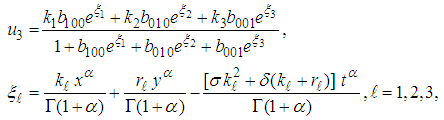(34)

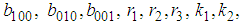where and 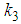are arbitrary constants. Equation (34) displays a three-kink wave solution of the (2+1) space-time fractional Burgers equation.

4.4. Four-Wave Solution

Suppose that equation (24) admits a solution of the form

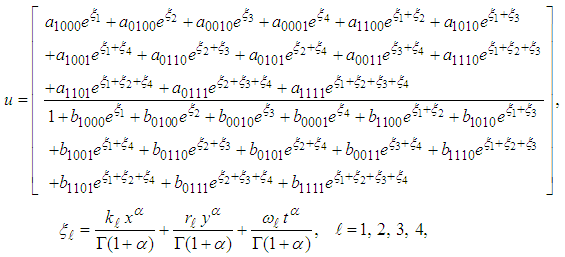(35)

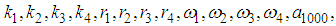
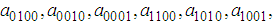
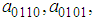
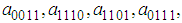
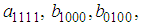
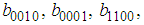
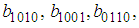
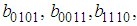
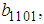
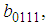where and 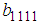are unknown constants to be determined. Substituting (35) into equation (24) with (26), we obtain a four-wave solution to the (2+1) space-time fractional Burgers equation as

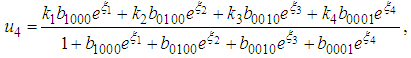(36)

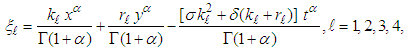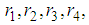
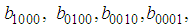
Where and 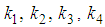are arbitrary constants. Equation (36) displays a four-kink wave solution of the space-time fractional (2+1) Burgers equation.

5. The Space-Time Fractional (2+1) Sharma–Tasso–Olver Equation

When 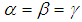, equation (21) becomes

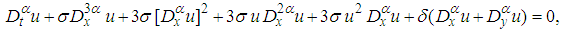(37)

which is called the (2+1) space-time fractional Sharma–Tasso–Olver equation. Doing the same manner, we obtain the single-wave solution as

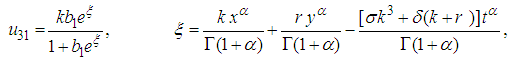(38)

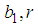where and 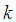are arbitrary constants. The double-wave solution of equation (37) takes the form

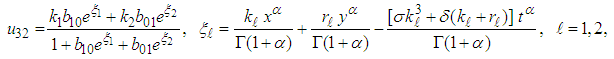(39)

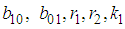where and 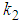are arbitrary constants. The three-wave solution is

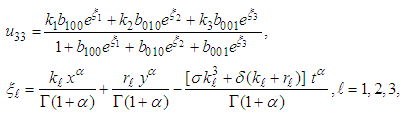(40)

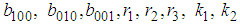where and 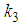are arbitrary constants. The four-wave solution of the space-time fractional Sharma–Tasso–Olver equation is

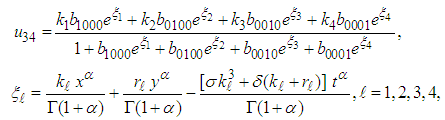(41)

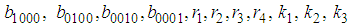where and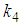 are arbitrary constants.

6. The (2+1) Space-Time Fractional Fourth Order Burgers Equation

When 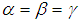, equation (22) becomes

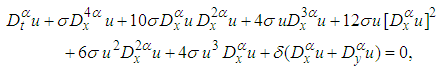(42)

which is called the (2+1) space-time fractional fourth order Burgers equation. The single-wave solution of equation (42) is

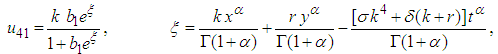(43)

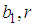where and 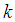are arbitrary constants. The double-wave solution to the (2+1) space-time fractional fourth order Burgers equation is

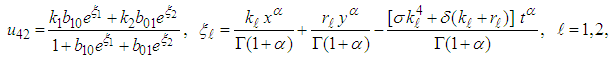(44)

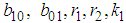where and 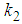are arbitrary constants. The three-wave solution to the (2+1) space-time fractional fourth order Burgers equation is

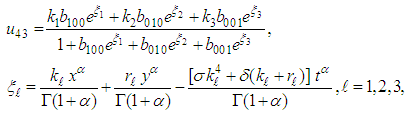(45)

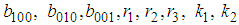where and 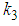are arbitrary constants. The four-wave solution of equation (45) is

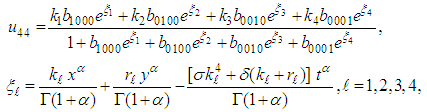(46)

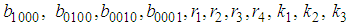where and 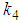are arbitrary constants.

7. The (2+1) Space-Time Fractional Fifth Order Burgers Equation

When 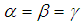, equation (23) becomes

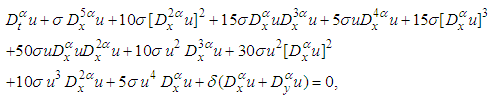(47)

which is called the (2+1) space-time fractional fifth order Burgers equation. Equation (47) admits a single-kink wave solution in the form

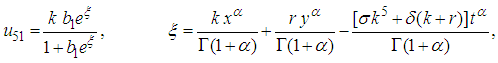(48)

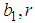where and 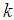are arbitrary constants. The double-kink wave solution of the (2+1) space-time fractional fifth order Burgers equation is

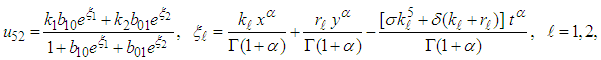(49)

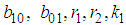where and 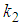are arbitrary constants. The three-kink wave solution of the (2+1) space-time fractional fifth order Burgers equation takes the form

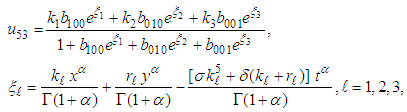(50)

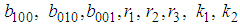where and 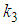are arbitrary constants. The four-kink wave solution of the (2+1) space-time fractional fifth order Burgers equation is

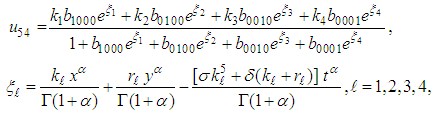(51)

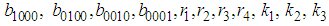where and 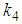are arbitrary constants.

Remark 1: When 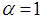, then the results are similar to those obtained by [54].

8. Conclusions and Discussions

In this paper, the hierarchy of the (2+1) space-time fractional Burgers equation is introduced. A direct and systematic solution procedure for constructing multi-wave solutions to nonlinear FDEs is proposed. The Exp-function method is extended to obtain multi-wave solution of the nonlinear FDEs successfully. As applications, new exact solutions for the (2+1) space-time fractional Burgers equation, the (2+1) space-time fractional Sharma-Tasso-Olver equation, the (2+1) space-time fractional fourth order Burgers equation and the (2+1) space-time fractional fifth order Burgers equation were obtained. In each of the cases the single-wave, the double-wave, the three-wave and the four-wave solutions were studied. This method can be applied to other FDEs.