Aiyesimi Y. M. 1, Jiya M. 1, Olayiwola R. O. 1, Wachin A. A. 2
1Department of Mathematics & Statistic, Federal University Technology, Minna, Nigeria
2Department of Mathematics & Computer, Ibrahim Badamasi Babangida University, Lapai, Nigeria
Correspondence to: Wachin A. A. , Department of Mathematics & Computer, Ibrahim Badamasi Babangida University, Lapai, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper presents magnetohydrodynamic (MHD) flow of unsteady convective third grade fluid in a cylindrical system. The non-linear governing equations were solved analytically using homotopy perturbation method (HPM). The influences of dimensionless parameters on magnetohydrodynamic (MHD) flow of a convective third grade fluid in a cylindrical system were investigated. Simulation results revealed that temperature and the velocity depend on the values of combination of magnetic field and porosity. The obtained results are presented graphically and discussed. It is observed that velocity decreases and increases with increasing magnetic field and porosity, temperature increases as magnetic field increases.
Keywords:
Magnetohydrodynamic, Perturbation, Convective Third grade fluid
Cite this paper: Aiyesimi Y. M. , Jiya M. , Olayiwola R. O. , Wachin A. A. , Mathematical Analysis of Convective Flow of an Unsteady Magnetohydrodynamic (MHD) Third Grade Fluid in a Cylindrical Channel, American Journal of Computational and Applied Mathematics , Vol. 6 No. 2, 2016, pp. 103-108. doi: 10.5923/j.ajcam.20160602.10.
1. Introduction
In most recent years, authors carried out investigation and problem dealing with the flow of non-Newtonian fluid in a cylindrical system. This interest is due to several important applications in engineering and industry such as reactive polymer flows in heterogeneous porous media, extraction of crude oil from the petroleum production, synthetic fibres and paper production (Schowaller 1978). Many practical situations we have deals with the natural convection of heat which play significant role in the behaviour of the flow.Convection problems associate will heat sources within fluid saturated porous media are of great practical signification, such as in geophysics and energy related problems (petroleum resources, geophysical flows, cooling of underground electric cable e.t.c). In generally terms, the difference between Non-Newtonian fluids and the single component Newtonian fluid in that, in the latter case the mathematical formulation is known but the macroscopic physical processes are complex and often not well understood, especially for turbulent flow conditions are for Non - Newtonian fluids even the appropriation governing equations and conditions at the boundaries are still not well understood. However, the flow of Non - Newtonian fluids plays an important role in many practical applications. Sajid et al (2008) discussed the effect of variable viscosity on the flow and heat transfer in a thin film flow for a third grade fluid. The thin film was considered on the outer side of an infinitely long vertical cylinder. The governing non-linear differential equation of momentum and energy were solved analytically by using homotopy analysis method (HAM). The study of MHD convection in a vertical channel, Aiyesimi et al. (2013) considered the MHD heat transfer in the flow between 2 concentric cylinders.Siddiqui et al (2012) carried out studies on two phase flow of a third grade fluid between parallel plates in three different cases. Makinde et al. (2010) studied MHD mixed convection from a vertical plate embedded in a porous medium with a convective boundary condition. Chamkha and Ahmad (2012) investigated unsteady MHD heat and mass transfer by mixed convection flow in the forward stagnation region of a rotating sphere at different wall conditions. Unsteady MHD convective heat and mass transfer in a boundary layer slip flow part a vertical permeable with thermal radiation and chemical reaction was examined by Dulal and Talukdar (2000). Singh and Pathak (2010) studied effect of slip condition on rotating vertical channel. Kandasamy et al. (2011) group theory transformation for Soret and Dufour effects on free convective heat and mass transfer with thermophoresis and chemical reaction over a porous stretching surface in the presence of heat source/sink. Rao et al. (2012) have found out the chemical effects on an unsteady MHD free convection fluid past a semi-infinite vertical plate embedded in a porous medium with heat absorption.In this paper, magnetohydrodynamics (MHD) flows of an unsteady convective third grade fluid in a cylindrical system were investigated. The governing equations arising from the unsteady flow are solved using homotopy perturbation method (HPM).
2. Model Formulation
The one-dimensional momentum and energy equations describing MHD flows of an unsteady convective third grade fluid in a cylindrical system are:Momentum equation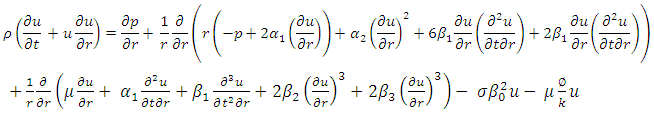 | (1) |
Energy equation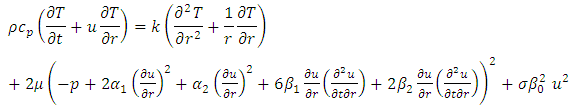 | (2) |
together with initial and boundary conditions 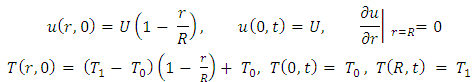 | (3) |
where u is velocity, p is pressure, k is the thermal conductivity, T is the temperature, 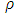 is the fluid
is the fluid 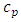 specific heat,
specific heat, 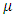 fluid viscosity,
fluid viscosity, 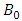 applied magnetic field, t is the non-dimensional time,
applied magnetic field, t is the non-dimensional time, 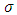 electrical conductivity.Here, equations (1) – (3) are transformed using the following coordinate transformations:
electrical conductivity.Here, equations (1) – (3) are transformed using the following coordinate transformations: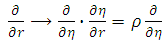 | (4) |
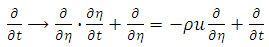 | (5) |
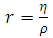 | (6) |
and we obtain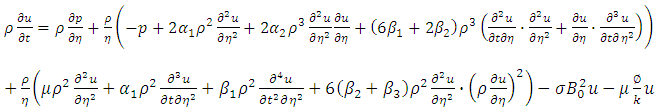 | (7) |
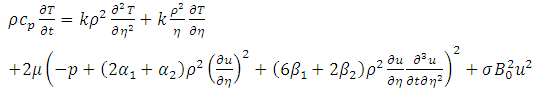 | (8) |
together with initial and boundary conditions;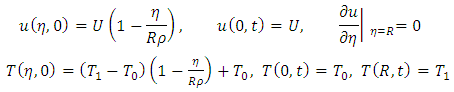 | (9) |
3. Method of Solution
3.1. Non-dimensionalization
Here, we let pressure p be constant and non-dimensionlised equations (7) – (9) using the following dimensionless variables, | (10) |
and obtain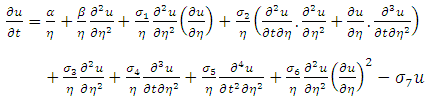 | (11) |
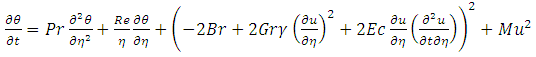 | (12) |
together with initial and boundary conditions: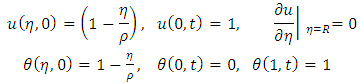 | (13) |
where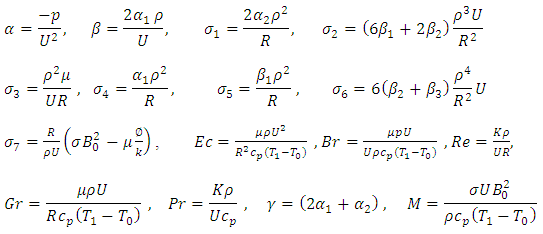
3.2. Existence and Uniqueness of Solution
Theorem 3.1: Let 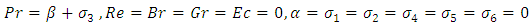 . Then, the equations (11) and (12) with initial and boundary conditions (13) has a unique solution for all
. Then, the equations (11) and (12) with initial and boundary conditions (13) has a unique solution for all  .Proof; Let
.Proof; Let 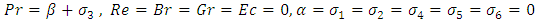 . In equations (11) and (12), we obtain
. In equations (11) and (12), we obtain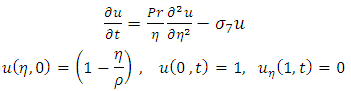 | (14) |
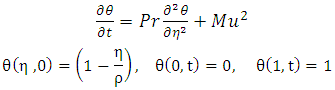 | (15) |
Using frobenius method, we obtain the solution of problem (14) as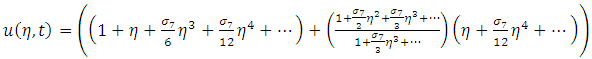 | (16) |
where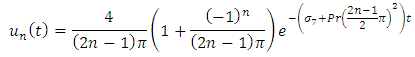 and using eigenfunction expansion method, the solution of problem as
and using eigenfunction expansion method, the solution of problem as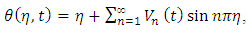 | (17) |
where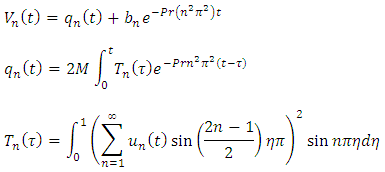 Hence, there exists a unique solution of problems (11) and (12). This completes the proof.
Hence, there exists a unique solution of problems (11) and (12). This completes the proof.
3.3. Analytical Solution
Applying homotopy perturbation method (HPM), we have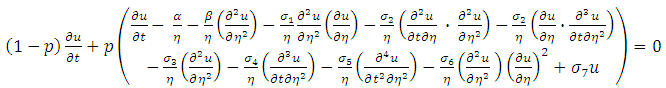 | (18) |
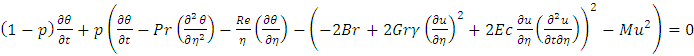 | (19) |
with initial and boundary condition 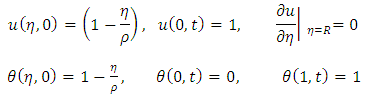 | (20) |
Therefore, we obtain the following at zero order:Momentum equation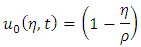 Energy equation
Energy equation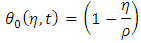 at first - order Problem, we haveMomentum equation:
at first - order Problem, we haveMomentum equation: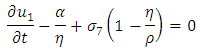
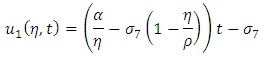 Energy equation:
Energy equation: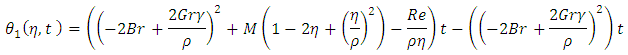 we let
we let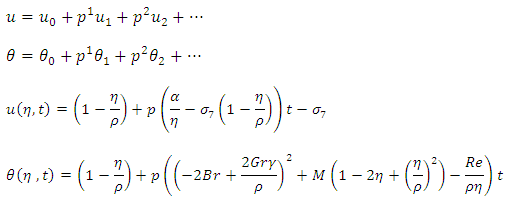 The computations were done using algebraic package MAPLE.
The computations were done using algebraic package MAPLE.
4. Results and Discussion
The analytical results obtained are shown through graphs which demonstrate the various parameter on the velocity and temperature of magnetohyrodynamic (MHD) flow of a convective third grade fluid in a cylindrical system by using homotopy perturbation method (HPM). We prove the existence and unigueness of solution by the actural method.
5. Discussion
The effect of 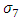 (combination of magnetic field and porosity) on velocity (u) for
(combination of magnetic field and porosity) on velocity (u) for 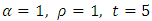 is shown in fig.1. It is observed that, velocity (u) decreases with combination of magnetic field and porosity increases. Fig.2, Shows the effect of
is shown in fig.1. It is observed that, velocity (u) decreases with combination of magnetic field and porosity increases. Fig.2, Shows the effect of 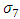 (combination of magnetic field and porosity) on velocity (u) for
(combination of magnetic field and porosity) on velocity (u) for 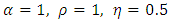 . We noted that, the velocity (u) increases with magnetic field and porosity increases.The effect of magnetic field (M) on temperature (T) for
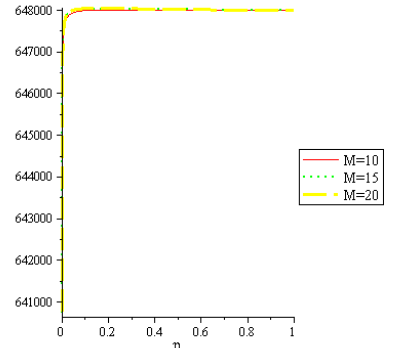
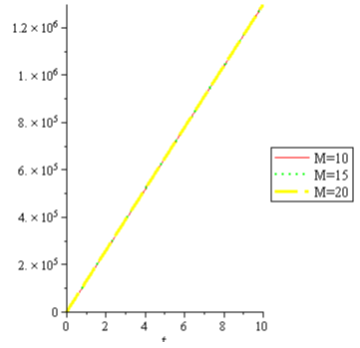
. We noted that, the velocity (u) increases with magnetic field and porosity increases.The effect of magnetic field (M) on temperature (T) for 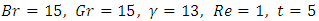 is shown in fig.3, it is observed that temperature (T) increases with magnetic field increases. It is also found that, in fig. 4 as temperature (T) increases, magnetic field increases for
is shown in fig.3, it is observed that temperature (T) increases with magnetic field increases. It is also found that, in fig. 4 as temperature (T) increases, magnetic field increases for 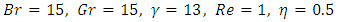 .
.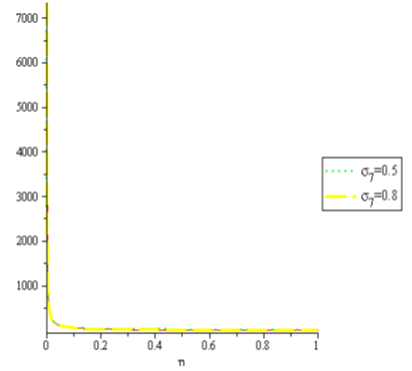 | Figure 1. |
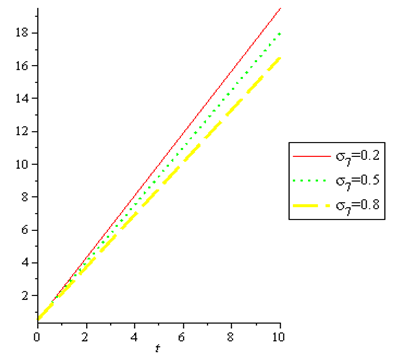 | Figure 2. |
 | Figure 3. |
 | Figure 4. |
6. Conclusions
The MHD flows of unsteady convective third grade fluid in cylindrical systems were examined. The resulting equations were solved using HPM and graphical results were obtained. The unsteady flow study were analysed through the effects of physical parameters such as Magnetic field on velocity and temperature distribution.
References
| [1] | Aiyesimi, Y. M, Okedayo, G.T. and Lawal, O. W. (2013). Unsteady MHD Thin Film Flow of a Third Grade Fluid With Heat Transfer and No Slip Boundary Conditions Down an Inclined Plane. International Journal of Scientific & Engineering Research, Volume 4(6), 420-438. |
| [2] | Chamkha, A. J. and Ahmed, S.E. (2012) “Unsteady MHD heat and mass transfer by mixed convection flow in the forward stagnation region of a rotating sphere at different wall conditions,” Chemical Engineering Communications, vol. 199, pp.122-141. |
| [3] | Kandasamy, R. Hayat, T. and Obaidat, S. (2011) “Group theory transformation for Soret and Dufour effects on free convective heat and mass transfer with thermophoresis and chemical reaction over a porous stretching surface in the presence of heat source/sink,” Nuclear Engineering and Design, vol. 241, pp. 2155-2161. |
| [4] | Makinde, O. D. And Aziz, A. (2010) “MHD mixed convection from a vertical plate embedded in a porous medium with a convective boundary condition,” International Journal of Thermal Sciences, vol. 49, pp. 1813-1820. |
| [5] | Pal, D. and Talukdar, B. (2000) “Perturbation analysis of unsteady magneto hydro dynamic convective heat and mass transfer in a boundary layer slip flow past a vertical permeable plate with thermal radiation and chemical reaction,” Communications in Nonlinear Science and Numerical Simulation, pp.1813-1830. |
| [6] | Rao, J.A. Sivaiah, S. and Raju, R. S. (2012) “Chemical effects on an unsteady MHD free convection fluid past a semi-infinite vertical plate embedded in a porous medium with heat absorption” JAFM, vol. 5(3), pp. 63-70. |
| [7] | Sajid M, Awals M, Nadeem S, and Hagat T. (2008). “The influence of slip condition on thin film flow of a fourth grade fluid by the homotopy analysis” comput Math Appl. 56, 2019 – 2026. |
| [8] | Siddiqui, A. M, Mitkova, M.K and Ansari, A. R. (2012). “Two – Phase Flow of a Third Grade Fluid between Parallel Plates. WSEAS Transactions on fluid mechanics. Issuue 4, volume 7, pp. 117- 128”. |
| [9] | Singh K. D. and Pathak, R. (2010) “An analysis of an oscillatory rotating MHD Poiseuille. Proc Nat Acad Sci India,” vol. 76 (4), pp. 201-207. |



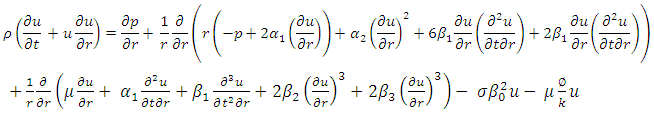
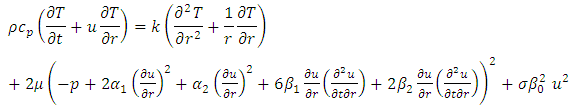
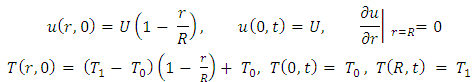
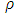 is the fluid
is the fluid 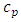 specific heat,
specific heat, 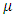 fluid viscosity,
fluid viscosity, 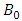 applied magnetic field, t is the non-dimensional time,
applied magnetic field, t is the non-dimensional time, 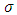 electrical conductivity.Here, equations (1) – (3) are transformed using the following coordinate transformations:
electrical conductivity.Here, equations (1) – (3) are transformed using the following coordinate transformations: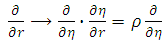
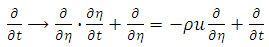
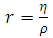
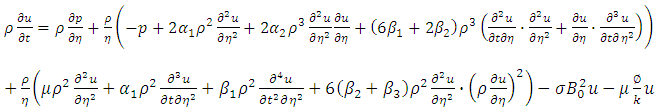
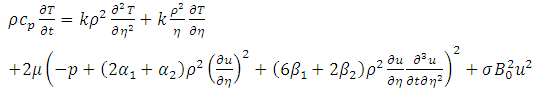
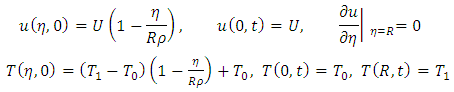

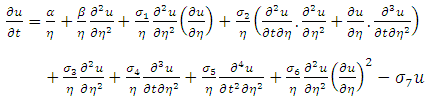
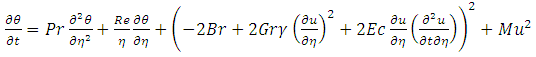
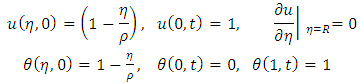
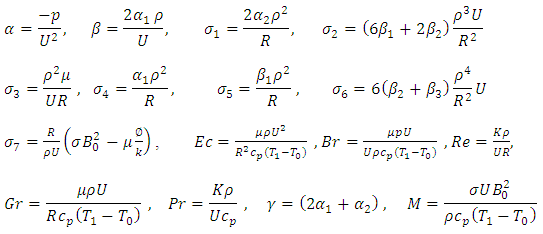
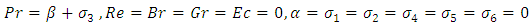 . Then, the equations (11) and (12) with initial and boundary conditions (13) has a unique solution for all
. Then, the equations (11) and (12) with initial and boundary conditions (13) has a unique solution for all 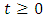 .Proof; Let
.Proof; Let 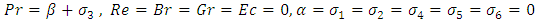 . In equations (11) and (12), we obtain
. In equations (11) and (12), we obtain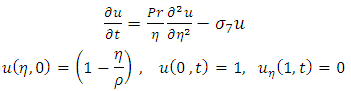
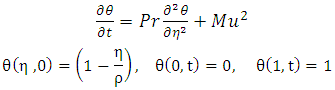
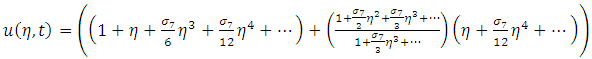
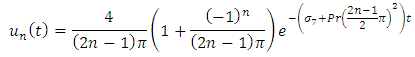 and using eigenfunction expansion method, the solution of problem as
and using eigenfunction expansion method, the solution of problem as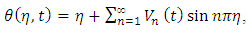
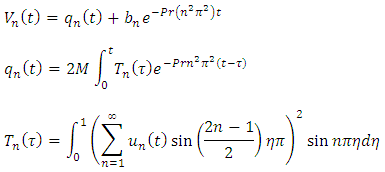 Hence, there exists a unique solution of problems (11) and (12). This completes the proof.
Hence, there exists a unique solution of problems (11) and (12). This completes the proof.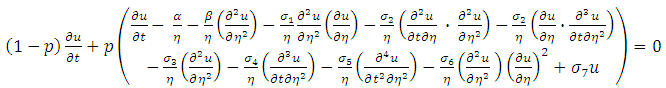
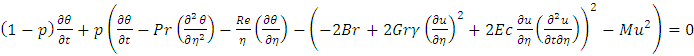
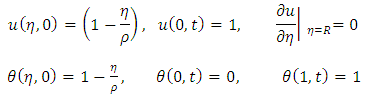
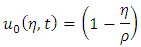 Energy equation
Energy equation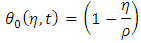 at first - order Problem, we haveMomentum equation:
at first - order Problem, we haveMomentum equation: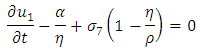
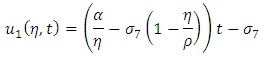 Energy equation:
Energy equation: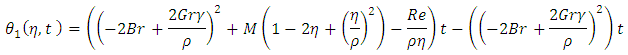 we let
we let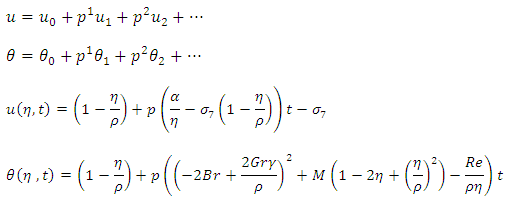 The computations were done using algebraic package MAPLE.
The computations were done using algebraic package MAPLE. (combination of magnetic field and porosity) on velocity (u) for
(combination of magnetic field and porosity) on velocity (u) for  is shown in fig.1. It is observed that, velocity (u) decreases with combination of magnetic field and porosity increases. Fig.2, Shows the effect of
is shown in fig.1. It is observed that, velocity (u) decreases with combination of magnetic field and porosity increases. Fig.2, Shows the effect of 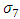 (combination of magnetic field and porosity) on velocity (u) for
(combination of magnetic field and porosity) on velocity (u) for 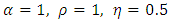 . We noted that, the velocity (u) increases with magnetic field and porosity increases.The effect of magnetic field (M) on temperature (T) for
. We noted that, the velocity (u) increases with magnetic field and porosity increases.The effect of magnetic field (M) on temperature (T) for 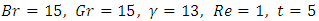 is shown in fig.3, it is observed that temperature (T) increases with magnetic field increases. It is also found that, in fig. 4 as temperature (T) increases, magnetic field increases for
is shown in fig.3, it is observed that temperature (T) increases with magnetic field increases. It is also found that, in fig. 4 as temperature (T) increases, magnetic field increases for 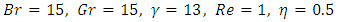 .
.



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML