-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(2): 65-73
doi:10.5923/j.ajcam.20160602.06

Dynamic Output Feedback Controller Design for a Class of Takagi-Sugeno Descriptor Systems
Boutayna Bentahra, Jalal Soulami, El mahfoud El Bouatmani, Abdellatif El Assoudi, El Hassane El Yaagoubi
ECPI, Department of Electrical Engineering, ENSEM, University Hassan II of Casablanca, Casablanca, Morocco
Correspondence to: Jalal Soulami, ECPI, Department of Electrical Engineering, ENSEM, University Hassan II of Casablanca, Casablanca, Morocco.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper considers the design problem of dynamic output feedback controller for a class of nonlinear descriptor systems described by Takagi-Sugeno (T-S) fuzzy models with measurable premise variables. The approach is based on the separation between dynamic and static relations in the descriptor model. The convergence of the closed-loop state system is studied by using the Lyapunov theory and the stability conditions are given in terms of linear matrix inequalities (LMIs). In practice, the computation of solutions of descriptor systems requires the combination of an ordinary differential equation (ODE) routine together with an optimization algorithm. The main result of this paper consists in showing that the dynamic output feedback controller problem for a class of T-S descriptor systems can be achieved by using a fuzzy controller based on an ODE structure only. Finally, simulation results are provided in order to show the validity of the proposed method.
Keywords: Fuzzy dynamic output feedback controller, Takagi-Sugeno descriptor systems, Measurable premise variables, Linear matrix inequality (LMI)
Cite this paper: Boutayna Bentahra, Jalal Soulami, El mahfoud El Bouatmani, Abdellatif El Assoudi, El Hassane El Yaagoubi, Dynamic Output Feedback Controller Design for a Class of Takagi-Sugeno Descriptor Systems, American Journal of Computational and Applied Mathematics , Vol. 6 No. 2, 2016, pp. 65-73. doi: 10.5923/j.ajcam.20160602.06.
Article Outline
1. Introduction
- In practice, in order to realize a feedback stabilization, we must know the state of the system. This state can be obtained by several ways. One way consists to design an observer. The theory which combines the couple (observer, controller system) is variously called separation principle, dynamic output feedback controller or observer-based controller. In this paper, we are concerned with the separation approach to the design of stabilizing output feedback control using T-S fuzzy observer.Recall that, T-S models [1] have been widely used for analysis and controller synthesis of nonlinear systems. The advantage of such approach relies on the fact that once the T-S fuzzy models are obtained, some analysis and design tools developed in the linear case can be used, which facilitates observer or/and controller synthesis for complex nonlinear systems see for example [2] and the references therein. However, many research on T-S fuzzy control and state observation for nonlinear systems described by ordinary differential equations (ODEs) exist in the literature. Indeed, the stability and the stabilization of such systems are mainly investigated through the direct Lyapunov method [3], [4]. Likewise, various works have been proposed to design observers [5-8]. The observer-based controller synthesis has been studied extensively with great success for such nonlinear systems. We may cite [9-13]. For nonlinear descriptor systems described by T-S models, the problems of control and observation design are mainly investigated in the literature, see for instance [14-17]. Notice that, generally an interesting way to solve the various problems raised previously (control and observation) is to write the convergence conditions on the LMI form.In this paper, we deal with descriptor nonlinear systems. In fact, many chemical and physical processes can be described by nonlinear systems of differential and algebraic equations [18-20]. These systems are variously called descriptor systems, singular systems, or differential algebraic equations (DAEs). This formulation includes both dynamic and static relations. The numerical simulation of such descriptor models usually combines an ODE numerical method together with an optimization algorithm.The main contribution of this paper is to give an observer-based controller design for a class of T-S descriptor models with measurable premise variables. A new design methodology through judicious use of the inequality of Young is proposed. The developed result is based on the separation between the dynamic and static relations in the descriptor model. The asymptotic stability of the closed-loop state system is studied by using the Lyapunov theory and the stability conditions are given in terms of LMIs. Besides, the proposed dynamic controller for a class of T-S descriptor systems can be synthesized by only an ODE structure.The outline of the paper is as follows. The class of the fuzzy T-S structure of nonlinear descriptor systems is introduced in Section 2. The main result about fuzzy observer-based controller design for a class of T-S descriptor models with measurable premise variables is stated in sections 3. The control and observer gains are found directly from LMI formulation. An illustrative application is given in Section 4 to show the efficiency of the proposed approach.In this paper, some notations used are fair standard. For example,
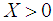 means the matrix
means the matrix 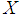 is symmetric and positive definite.
is symmetric and positive definite. 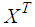 denotes the transpose of
denotes the transpose of 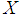 . The symbol
. The symbol 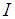 (or 0) represents the identity matrix (or zero matrix) with appropriate dimension, and
(or 0) represents the identity matrix (or zero matrix) with appropriate dimension, and 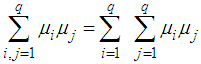 .
.2. System Description
- In this paper, the following class of T-S descriptor systems is considered:
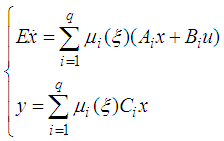 | (1) |
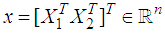 is the state vector with
is the state vector with 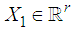 is the vector of differential variables,
is the vector of differential variables, 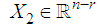 is the vector of algebraic variables,
is the vector of algebraic variables, 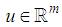 is the control input,
is the control input, 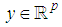 is the measured output.
is the measured output. 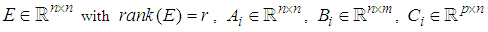 are real known constant matrices with:
are real known constant matrices with: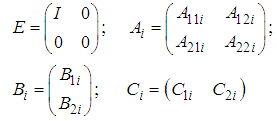 | (2) |
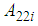 are supposed invertible
are supposed invertible 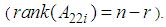 The premise variable
The premise variable 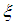 is supposed to be real-time accessible and depended only on
is supposed to be real-time accessible and depended only on 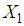 .
. 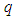 is the number of sub-models. The
is the number of sub-models. The 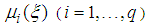 are the weighting functions that ensure the transition between the contribution of each sub model:
are the weighting functions that ensure the transition between the contribution of each sub model: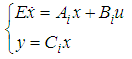 | (3) |
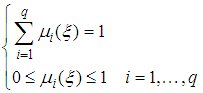 | (4) |
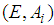 is regular, i.e.
is regular, i.e. 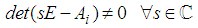 Assumption A2: All sub-models (3) are impulse controllable and stabilisable.Assumption A3: All sub-models (3) are impulse observable and detectable.The main objective of this work is to design an observer-based controller for system (1) which assures asymptotic convergence to zero of the closed-loop system. The approach is based on the separation between dynamic and static relations in each sub-model (3) and the global fuzzy model is obtained by aggregation of the resulting sub-models. So, using (2), system (3) can be rewritten as follows:
Assumption A2: All sub-models (3) are impulse controllable and stabilisable.Assumption A3: All sub-models (3) are impulse observable and detectable.The main objective of this work is to design an observer-based controller for system (1) which assures asymptotic convergence to zero of the closed-loop system. The approach is based on the separation between dynamic and static relations in each sub-model (3) and the global fuzzy model is obtained by aggregation of the resulting sub-models. So, using (2), system (3) can be rewritten as follows: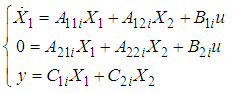 | (5) |
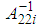 exist, the algebraic equations can be solved directly for algebraic variables, to obtain:
exist, the algebraic equations can be solved directly for algebraic variables, to obtain: 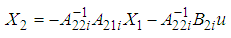 | (6) |
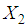 (equation (6) in equation (5) yields the following model:
(equation (6) in equation (5) yields the following model: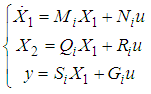 | (7) |
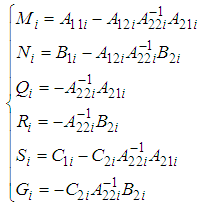 | (8) |
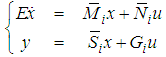 | (9) |
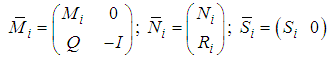 | (10) |
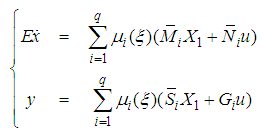 | (11) |
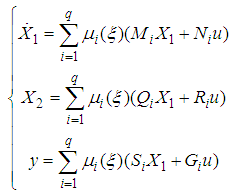 | (12) |
3. Main Results
- The objective is to design an observer-based controller for the T-S descriptor system (1). Therefore, first a new feedback controller design method is proposed. Secondly, an observer design approach permitting to estimate the unknown state is given.
3.1. Feedback Controller Design
- In this section, the goal is to determine the gains
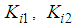 of the following control law:
of the following control law: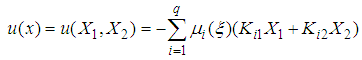 | (13) |
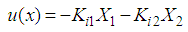 | (14) |
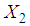 giving in (7) by:
giving in (7) by: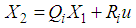 | (15) |
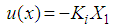 | (16) |
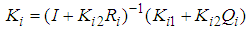 | (17) |
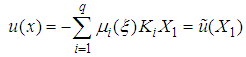 | (18) |
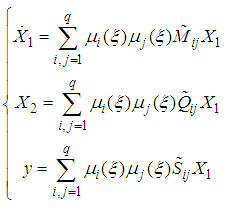 | (19) |
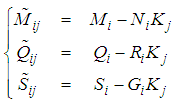 | (20) |
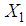 converges toward zero. Then, the following result can be stated.Theorem 1.: The closed-loop system described by (19) is globally exponentially stable if there exist matrices
converges toward zero. Then, the following result can be stated.Theorem 1.: The closed-loop system described by (19) is globally exponentially stable if there exist matrices 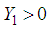 ,
, 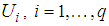 verifying the following LMIs:
verifying the following LMIs: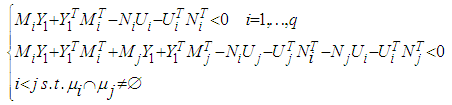 | (21) |
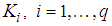 are given by:
are given by: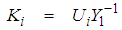 | (22) |
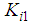 and
and 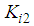 given in (13), according to the expression of
given in (13), according to the expression of 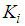 given in (17), it is clear that we have:
given in (17), it is clear that we have: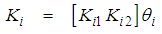 | (23) |
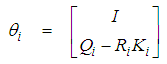 | (24) |
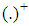 is given by:
is given by: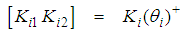 | (25) |
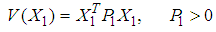 | (26) |
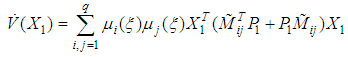 | (27) |
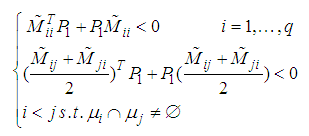 | (28) |
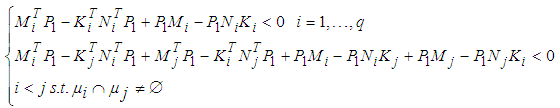 | (29) |
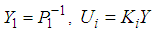 . Premultiply and postmultiply (29) by
. Premultiply and postmultiply (29) by  , to obtain the LMI conditions given in (21). From the Lypunov stability theory, if the LMI conditions (21) are satisfied, the closed-loop system (19) is exponentially asymptotically stable. This completes the proof of Theorem 1.
, to obtain the LMI conditions given in (21). From the Lypunov stability theory, if the LMI conditions (21) are satisfied, the closed-loop system (19) is exponentially asymptotically stable. This completes the proof of Theorem 1.3.2. Observer Design
- As it was mentioned before, to apply state feedback control it is necessary to know all the states of the system. In real application, not all the states are available to be measured, thus the necessity to use an observer arises. Therefore, in this section, we propose an observer design for a class of T-S descriptor systems (1). Based on the form (12), the proposed observer takes the following form:
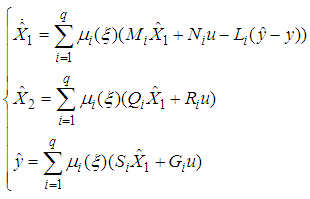 | (30) |
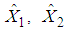 and
and 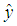 denote the estimated state vector and output vector respectively. The activation functions are the same than those used in the T-S model (15).
denote the estimated state vector and output vector respectively. The activation functions are the same than those used in the T-S model (15). 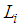 are the gains of observer witch are to determined such that
are the gains of observer witch are to determined such that 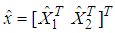 asymptotically converges to
asymptotically converges to 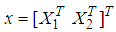 .Denoting the state estimation error by:
.Denoting the state estimation error by: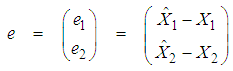 | (31) |
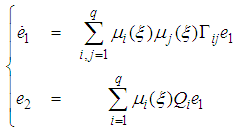 | (32) |
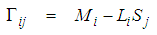 | (33) |
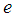 toward zero, it suffices to prove from (32), that
toward zero, it suffices to prove from (32), that 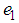 converges toward zero. The result is stated in the following theorem.Theorem 2.: There exists an observer (30) for (1) if there exist matrices
converges toward zero. The result is stated in the following theorem.Theorem 2.: There exists an observer (30) for (1) if there exist matrices 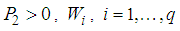 verifying the following LMIs:
verifying the following LMIs: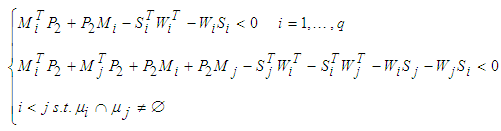 | (34) |
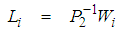 | (35) |
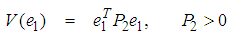 | (36) |
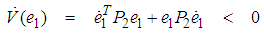 | (37) |
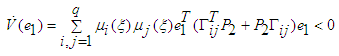 | (38) |
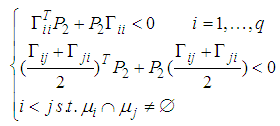 | (39) |
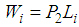 , it follows that (39) is equivalent to (34). From the Lypunov stability theory, if the LMI conditions (34) are satisfied, the estimated error equation (32) is exponentially asymptotically stable.
, it follows that (39) is equivalent to (34). From the Lypunov stability theory, if the LMI conditions (34) are satisfied, the estimated error equation (32) is exponentially asymptotically stable.3.3. Dynamic Output Feedback Controller Design
- In this section, we propose a novel approach for the separation principle theory of a class of T-S descriptor systems (1). A fuzzy dynamic output feedback controller for T-S descriptor system (1) is defined by:
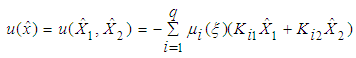 | (40) |
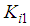 and
and 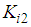 are the control gains to be determined.As in subsection 3.1, in order to be able to state the result in the form of LMIs, the key idea lies in the use of the equivalent control law of (40) given by:
are the control gains to be determined.As in subsection 3.1, in order to be able to state the result in the form of LMIs, the key idea lies in the use of the equivalent control law of (40) given by: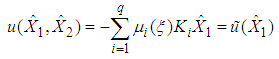 | (41) |
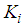 is defined in (17) which can be determined by Theorem 3 below and the control gains
is defined in (17) which can be determined by Theorem 3 below and the control gains 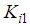 and
and 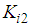 used in (40) can be determined by equation (25).Let
used in (40) can be determined by equation (25).Let 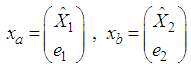 | (42) |
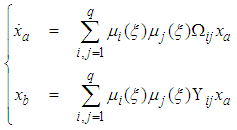 | (43) |
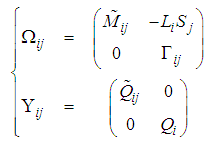 | (44) |
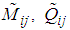 and
and 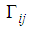 are defined in (20) and (33) respectively.The following theorem provides the main result of this paper.Theorem 3.: The closed-loop T-S model described by (43) is globally asymptotically stable if for a fixed scalar
are defined in (20) and (33) respectively.The following theorem provides the main result of this paper.Theorem 3.: The closed-loop T-S model described by (43) is globally asymptotically stable if for a fixed scalar 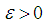 , there exist matrices
, there exist matrices 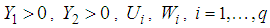 verifying the following LMIs:
verifying the following LMIs: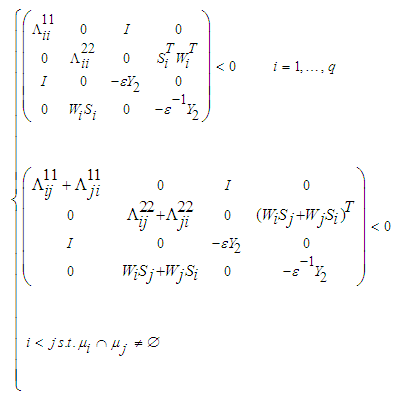 | (45) |
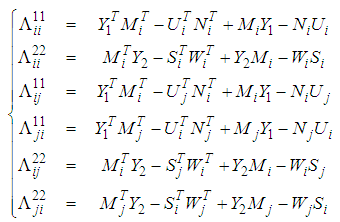 | (46) |
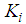 and
and 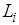 are given by:
are given by: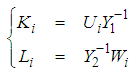 | (47) |
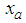 converges toward zero. Thus, let us consider the candidate Lyapunov function as follows:
converges toward zero. Thus, let us consider the candidate Lyapunov function as follows: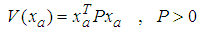 | (48) |
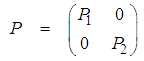 | (49) |
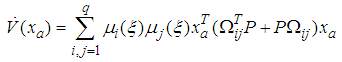 | (50) |
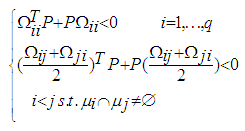 | (51) |
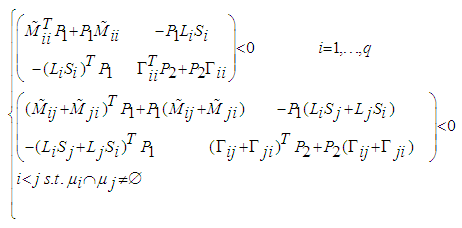 | (52) |
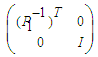 and
and 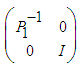 respectively and defining new variables
respectively and defining new variables 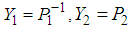 we obtain:
we obtain: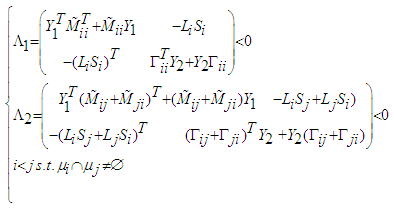 | (53) |
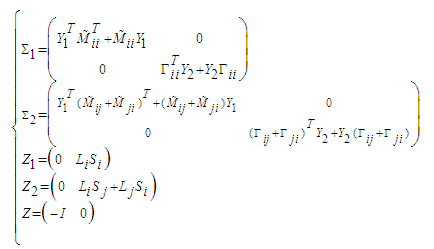 | (54) |
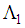 and
and 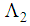 can be rewritten again as:
can be rewritten again as: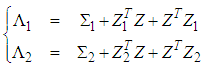 | (55) |
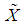 and
and 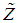 with appropriate dimensions, the following property holds for any invertible matrix
with appropriate dimensions, the following property holds for any invertible matrix 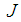 and scalar
and scalar 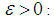
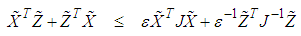 | (56) |
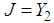 , (55) becomes:
, (55) becomes: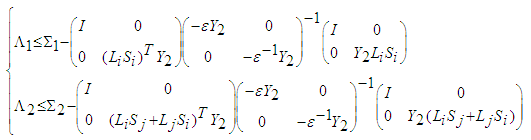 | (57) |
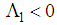 and
and 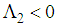 hold if the following two matrix inequalities are satisfied.
hold if the following two matrix inequalities are satisfied.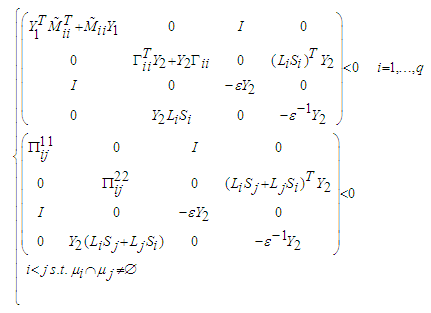 | (58) |
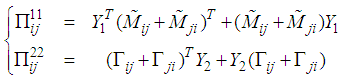 | (59) |
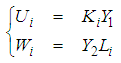 | (60) |
4. Application to an Inverted Pendulum System
- To illustrate the effectiveness of the proposed method, we consider a nonlinear inverted pendulum system controlled by a separately excited direct-current (DC) motor [22]. Using the procedure of fuzzy model construction given in [23], the following T-S descriptor model with measurable premise variables can be derived:
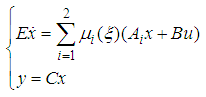 | (61) |
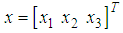 is the state vector,
is the state vector, 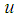 denotes the control input voltage,
denotes the control input voltage, 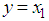 is the measured output.
is the measured output. 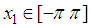 is the angle of the pendulum,
is the angle of the pendulum, 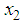 is the angular velocity,
is the angular velocity, 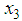 is the current of the motor.
is the current of the motor.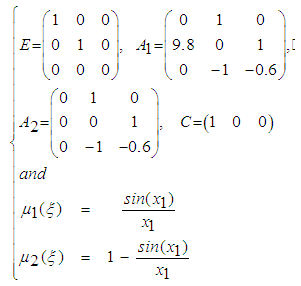 | (62) |
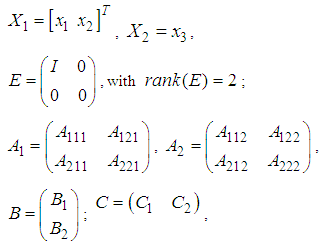 With:
With: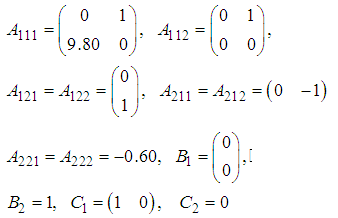 This show that the model (61) is a particular case of the system (1). Then, the fuzzy descriptor system (61) can be rewritten in the following equivalent form:
This show that the model (61) is a particular case of the system (1). Then, the fuzzy descriptor system (61) can be rewritten in the following equivalent form: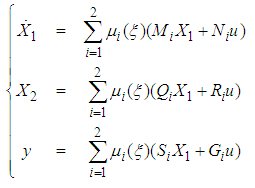 | (63) |
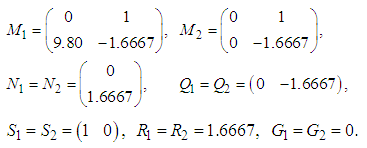 Consequently, using Theorem with , the following dynamic controller gains
Consequently, using Theorem with , the following dynamic controller gains 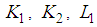 and
and 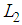 were obtained:
were obtained: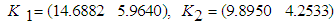 | (64) |
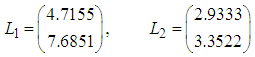 | (65) |
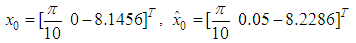 are presented in Figures 1, 2 and 3. These simulation results show the performance of the proposed observer-based controller designed with the parameters
are presented in Figures 1, 2 and 3. These simulation results show the performance of the proposed observer-based controller designed with the parameters 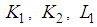 ,
, 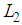 given by (64) - (65). They show that the global asymptotic stability of the closed loop T-S system with the control law is satisfied. Moreover, Figures 2 and 3 show that the observer gives a good estimation of angular velocity and current of the motor.
given by (64) - (65). They show that the global asymptotic stability of the closed loop T-S system with the control law is satisfied. Moreover, Figures 2 and 3 show that the observer gives a good estimation of angular velocity and current of the motor.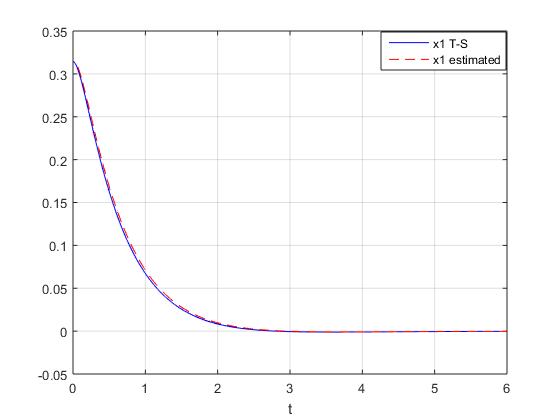 | Figure 1. 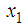 and and 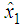 with fuzzy observer-based controller with fuzzy observer-based controller |
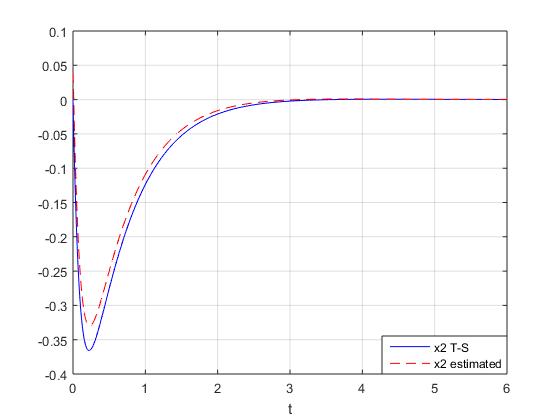 | Figure 2. 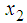 and and 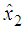 with fuzzy observer-based controller with fuzzy observer-based controller |
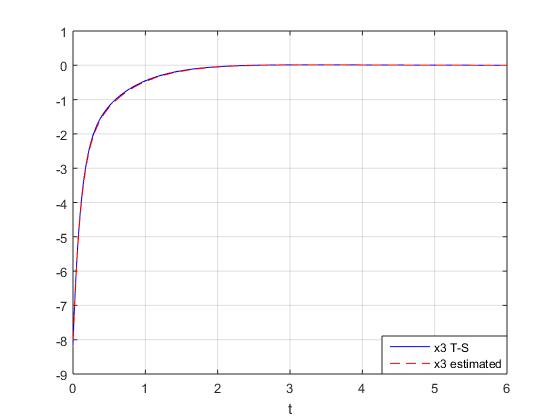 | Figure 3. 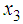 and and 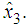 with fuzzy observer-based controller with fuzzy observer-based controller |
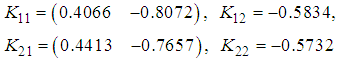 Notice that with these numerical values of
Notice that with these numerical values of 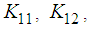
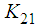 and
and 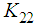 , we obtain exactly the same simulation results given in Figures 1, 2 and 3.
, we obtain exactly the same simulation results given in Figures 1, 2 and 3.5. Conclusions
- An observer-based fuzzy controller design approach for a class of T-S descriptor systems with measurable premise variables is proposed in this paper. The approach is based on the separation between dynamic and static relations in the descriptor model. The convergence of the closed-loop system is studied by using the Lyapunov theory and the stability conditions are given in terms of LMIs. Simulation results are given and demonstrate the good performance of the proposed dynamic controller.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML fuzzy output feedback control design for nonlinear dynamic systems: an LMI approach”, IEEE Transactions on Fuzzy Systems, 8(3), 249-265, June 2000.
fuzzy output feedback control design for nonlinear dynamic systems: an LMI approach”, IEEE Transactions on Fuzzy Systems, 8(3), 249-265, June 2000. approach”, Proceedings of the 17th world congress, the international federation of automatic control. Seoul, Korea, July 6-11, 2008.
approach”, Proceedings of the 17th world congress, the international federation of automatic control. Seoul, Korea, July 6-11, 2008.