Yusuf A.1, Aiyesimi Y. M.1, Jiya M.1, Okedayo G. T.2
1Department of Mathematics and Statistics, Federal University of Technology, Minna, Nigeria
2Department of Mathematics, Ondo State University of Science and Technology, Okiti-Pupa, Nigeria
Correspondence to: Yusuf A., Department of Mathematics and Statistics, Federal University of Technology, Minna, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The solution to the problem of laminar fluid flow in an inclined parallel walls resulting from the movement of the lower wall while the upper wall remain stationary (Coette flow) in a nanofluid with thermal convection, Soret and Dufour effects with radiation has been obtained using the Modified Adomian Decomposition Method for the first time. The model used for the nanofluid was presented in its rectangular coordinate system and incorporates the effect of Brownian motion, and thermophoresis parameter. A similarity solution is presented which depends on the Prandtl number 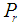 , Lewis number
, Lewis number 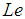 , Brownian motion
, Brownian motion 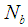 , thermophoresis number
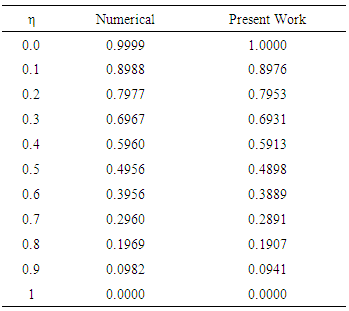
, thermophoresis number 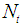 , Soret (Sr) number, Dufour (DU) number, and Grashof numbers GrT, Grc. It is found that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. A comparative analysis of present study was carried out with the numerical on Table 1, and it was observed the two method are in good agreement.
, Soret (Sr) number, Dufour (DU) number, and Grashof numbers GrT, Grc. It is found that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. A comparative analysis of present study was carried out with the numerical on Table 1, and it was observed the two method are in good agreement.
Keywords:
Adomian Decomposition Method, Nanofluid, Nanopaticles, Thermophoresis, Boundary layer, Convection, Radiation Channel flow, Soret number, Dufour number
Cite this paper: Yusuf A., Aiyesimi Y. M., Jiya M., Okedayo G. T., Analysis of Couette Flow of a Nanofluid in an Inclined Channel with Soret and Dufour Effects, American Journal of Computational and Applied Mathematics , Vol. 6 No. 2, 2016, pp. 57-64. doi: 10.5923/j.ajcam.20160602.05.
1. Introduction
From energy saving perspective, improvement of heat transfer performance in systems is very necessary. Low thermal conductivity of conventional heat transfer fluids such as water and oils is a primary limitation in enhancing the performance and the compactness of systems. Solids typically have a higher thermal conductivity than liquids. For example, copper (Cu) has a thermal conductivity 700 times greater than water and 3000 times greater than engine oil. An innovative and novel technique to enhance heat transfer is to use solid particles in the base fluid (i.e. nanofluids) in the range of sizes 10–50 nm. Abu-Nada et al. [1] investigated natural convection heat transfer enhancement in horizontal concentric annuli field by nanofluid. They found that for low Rayleigh numbers, nanoparticles with higher thermal conductivity produce more enhancements in heat transfer. Ellahi [2] studied magnetohydrodynamic (MHD) flow of non-Newtonian nanofluid in a pipe and observed that the MHD parameter decreases the fluid motion and the velocity profile is larger than that of the temperature profile even in the presence of variable viscosities. Free convection heat transfer in a concentric annulus between a cold square and heated elliptic cylinders in the presence of a magnetic field was investigated by Sheikholeslami et al. [3]. They found that enhancement in heat transfer increases as the Hartmann number increases but it decreases with increase of Rayleigh number. Rashidi et al. [4] considered the analysis of the second law of thermodynamics applied to an electrically conducting incompressible nanofluid fluid flowing over a porous rotating disk. They concluded that magnetic rotating disk drives have important applications in heat transfer enhancement in renewable energy systems. Sheikholeslami et al. [5] used heatline analysis to simulate two phase simulation of nanofluid flow and heat transfer. Their results indicated that the average Nusselt number decreases as the buoyancy ratio number increases until it reaches a minimum value and then starts increasing. Sheikholeslami et al. [6] studied the magnetic field effect on CuO–water nanofluid flow and heat transfer in an enclosure which is heated from below. They found that effect of Hartmann number and heat source length is more pronounced at high Rayleigh number. Effect of nanofluid on heat transfer enhancement has been investigated by different authors [7]. Aiyesimi et al [8] considers Hydromagnetic Boudary-Layer Flow of a Nanofluid Past a Stretching Sheet Embedded in a Darcian Porous Medium with Radiation and it was found out that at lower values of Prandtl number, heat able to diffuse more rapidly out of the system.In a recent paper Aiyesimi et al [9] extended the model of Khan and Pop [10] to analyse and investigate the convective boundary-layer flow of a nanofluid past a stretching sheet with radiation. It was observed that thermal buoyancy and nanofraction buoyancy enhances the fluid velocity, temperature, and nanofraction. It is appropriate to channelize the work of Aiyesimi et al [10] over an inclined channel with Soret and Dufour effects and use the Adomian Decomposition Method (ADM) to obtain the analytical solution of the model. This work is a new development in the literature in which an analytical solution of a convective boundary-layer flow of a nanofluid past a stretching channel with Soret and Dufour effects is proposed using the Adomian Decomposition Method.
2. Problem Formulation
A steady, two dimensional boundary layer flow of a nanofluid in an inclined channel at angle 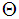 is considered. It is assumed that the wall located at
is considered. It is assumed that the wall located at 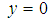 stretches with a velocity
stretches with a velocity 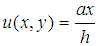 (couette flow), while the other wall at
(couette flow), while the other wall at 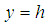 (h = is the width of the channel) remain stationary throughout the flow, where a is constant and
(h = is the width of the channel) remain stationary throughout the flow, where a is constant and 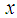 is the coordinate measured along the stretching wall. The temperature
is the coordinate measured along the stretching wall. The temperature 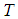 and the nanoparticle fraction
and the nanoparticle fraction 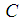 have constants values
have constants values 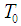 and
and 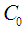 at
at 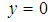 and
and 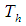 and
and 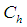 at
at 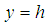 respectively. For this application, we will adopt the natural convection with Soret, Dufour, and Radiation effects for the formulation of Khan and Pop [10] and it is governed by the following equations:Continuity equation:
respectively. For this application, we will adopt the natural convection with Soret, Dufour, and Radiation effects for the formulation of Khan and Pop [10] and it is governed by the following equations:Continuity equation: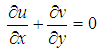 | (1) |
Momentum equation: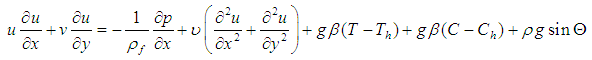 | (2) |
Energy equation:- 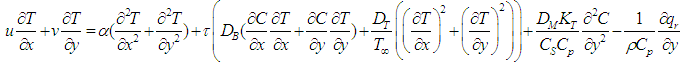 | (3) |
Nanofraction equation:-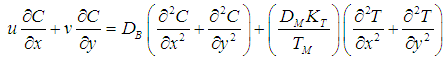 | (4) |
Subject to the boundary conditions: 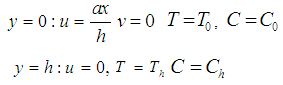 | (5) |
where 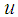 and
and 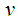 are the velocity components along the
are the velocity components along the 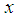 and
and 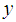 axes respectively,
axes respectively, 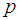 is the fluid pressure,
is the fluid pressure, 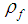 is the density of the base fluid,
is the density of the base fluid, 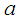 is the thermal diffusivity,
is the thermal diffusivity, 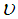 is the kinematic viscousity,
is the kinematic viscousity, 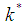 is the thermal conductivity,
is the thermal conductivity, 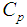 is the specific heat capacity at constant pressure,
is the specific heat capacity at constant pressure, 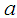 is a positive constant,
is a positive constant, 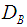 is the Brownian diffusion coefficient,
is the Brownian diffusion coefficient, 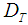 is the thermopheric diffusion coefficient and
is the thermopheric diffusion coefficient and 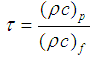 is the ratio between the effective heat capacity of the fluid with
is the ratio between the effective heat capacity of the fluid with 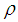 being the density,
being the density, 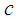 is the volumetric volume expansion coefficient and
is the volumetric volume expansion coefficient and 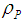 is the density of the particles g is the acceleration due to gravity,
is the density of the particles g is the acceleration due to gravity, 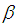 is the volumetric coefficient of thermal expansion,
is the volumetric coefficient of thermal expansion, 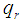 is the radiative heat flux
is the radiative heat flux 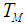 is the mean fluid temperature,
is the mean fluid temperature, 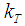 is the thermal diffusion ratio,
is the thermal diffusion ratio, 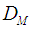 is the diffusion ratio,
is the diffusion ratio, 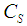 is concentration susceptibility.Following Roseland approximation we have
is concentration susceptibility.Following Roseland approximation we have 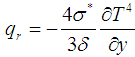 , where
, where 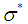 and
and 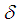 are the Stefan-Boltzmann constant and the mean absorption coefficient respectively. The temperature differences within the fluid is assumed sufficiently small such that
are the Stefan-Boltzmann constant and the mean absorption coefficient respectively. The temperature differences within the fluid is assumed sufficiently small such that 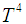 may be expressed as a linear function of Temperature. Expanding
may be expressed as a linear function of Temperature. Expanding 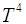 in Taylor’s series about
in Taylor’s series about 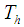 and neglecting higher order terms, we get
and neglecting higher order terms, we get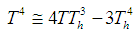 | (6) |
therefore, 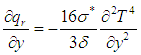 , Defining the dimensional stream function
, Defining the dimensional stream function 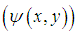 in the usual way such that
in the usual way such that 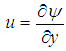 and
and 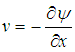 and following the work of Sheikholeslami [11] :-
and following the work of Sheikholeslami [11] :-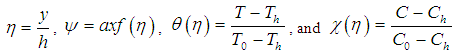 | (7) |
where 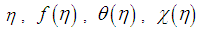 are the dimensionless fluid distance, velocity profile, temperature profile, and nanoparticle concentration.Neglecting the pressure gradient equations (1) to (6) reduces to the following local similarity solution:-
are the dimensionless fluid distance, velocity profile, temperature profile, and nanoparticle concentration.Neglecting the pressure gradient equations (1) to (6) reduces to the following local similarity solution:- 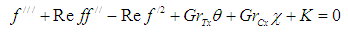 | (8) |
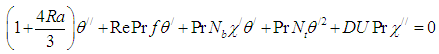 | (9) |
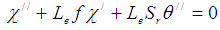 | (10) |
with corresponding boundary conditions: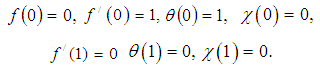 | (11) |
in which: 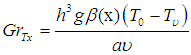 ,
, 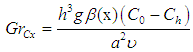 ,
, 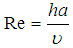 ,
, 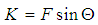
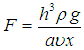 ,
, 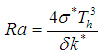 ,
, 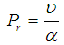
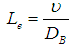 ,
, 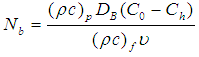
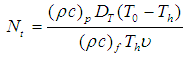
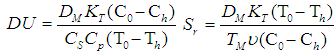 are the local Thermal Grashof number, local concentration Grashof number, Renold number, Gravitational parameter, Radiation, Prandtl number, Lewis number, Brownian motion parameter, thermophoresis parameter, Dufour number, Soret number, and Schmidt number, respectively. For the momentum equation to have a similarity solution, the parameters
are the local Thermal Grashof number, local concentration Grashof number, Renold number, Gravitational parameter, Radiation, Prandtl number, Lewis number, Brownian motion parameter, thermophoresis parameter, Dufour number, Soret number, and Schmidt number, respectively. For the momentum equation to have a similarity solution, the parameters 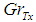 and
and 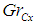 most be constant and not functions of
most be constant and not functions of 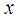 . This can be met if volumetric coefficient of thermal expansion
. This can be met if volumetric coefficient of thermal expansion 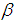 is proportional to
is proportional to 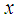 . We therefore assume
. We therefore assume 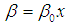 | (12) |
The nonlinear coupled differential equations in (8) to (10) with boundary conditions in (11) was solved using the Modified Adomian Decomposition as described by Ebaid and Al-Armani [12].
3. Results and Discussion
The nonlinear coupled differential equations (8) to (10) with boundary conditions (11) are solved using the Modfied Adomian Decomposition Methods. In order to assess the accuracy of the present method, we have compared our solution for 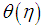 for different values of
for different values of 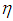 at
at 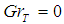 and
and 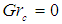 with the Numerical method as shown in Table 1. It was observed that the present method is in good agreement with the Numerical-Method.
with the Numerical method as shown in Table 1. It was observed that the present method is in good agreement with the Numerical-Method.Table 1. Comparison of Result for
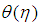 with the present work for with the present work for
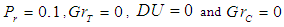
 |
| |
|
Figures 2 to 4 shows the effect of thermal Grashof number 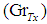 on the velocity profile, temperature and concentration profile and nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile and the nanofraction profile while the temperature profile reduces as the thermal Grashof number increases.
on the velocity profile, temperature and concentration profile and nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile and the nanofraction profile while the temperature profile reduces as the thermal Grashof number increases. 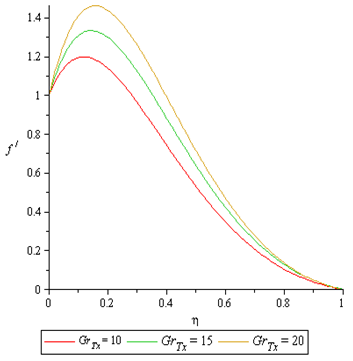 | Figure 2. Effect of 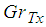 on Velocity Profile on Velocity Profile |
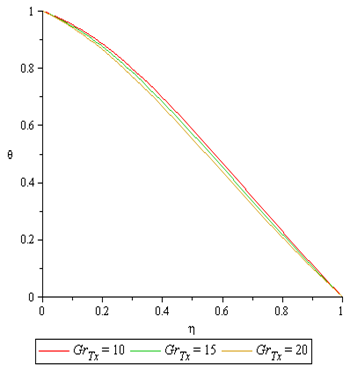 | Figure 3. Effect of 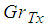 on Temperature Profile on Temperature Profile |
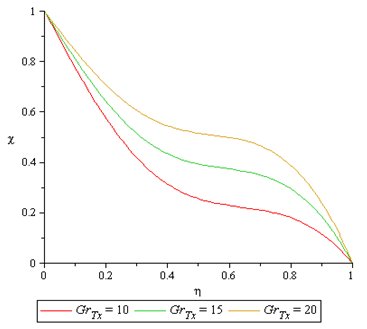 | Figure 4. Effect of 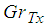 on Nanofraction Profile on Nanofraction Profile |
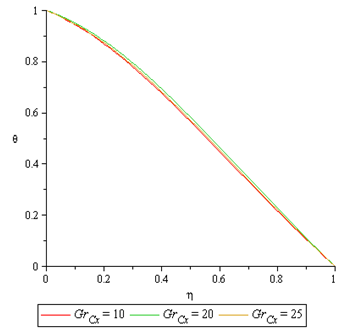
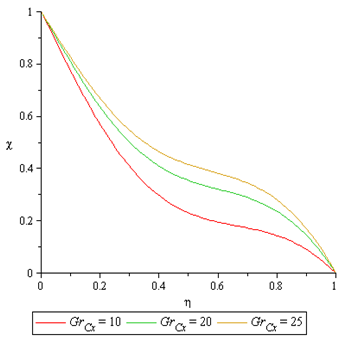
Figure 5 to 7 presents the effect of Concentration Grashof number 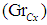 . On the velocity profile, temperature and Nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile at the lower wall (moving wall), where the fluid velocity is maximum and decreases the velocity profile faster for higher values of Concentration profile at the upper wall (stationary wall), where the flow velocity is minimum. The temperature profile and the nanofraction profiles are enhanced. This leads to increase in the boundary layers as shown in the graph.
. On the velocity profile, temperature and Nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile at the lower wall (moving wall), where the fluid velocity is maximum and decreases the velocity profile faster for higher values of Concentration profile at the upper wall (stationary wall), where the flow velocity is minimum. The temperature profile and the nanofraction profiles are enhanced. This leads to increase in the boundary layers as shown in the graph.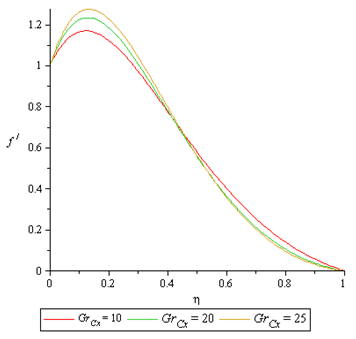 | Figure 5. Effect of 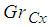 on Velocity Profile on Velocity Profile |
 | Figure 6. Effect of 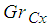 on Temperature Profile on Temperature Profile |
 | Figure 7. Effect of  on Nanofraction Profile on Nanofraction Profile |
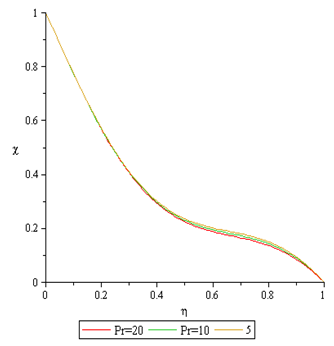
Figures 8 to 9 displays the effect of Prandtl number (Pr) on the temperature profile and the concentration profile. The thermal boundary thickness decreases for both temperature and concentration profile as the Prandtl number decreases. The reason is that higher values of Prandtl number are equivalent to increase in the thermal conductivity of the fluid and therefore heat is able to diffuse away from the heated surface more rapidly for lower values of Prandtl number. Hence there is a reduction in temperature with decrease in the Prandtl number.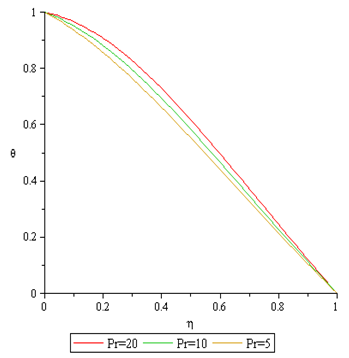 | Figure 8. Effect of Pr number on Temperature Profile |
 | Figure 9. Effect of Pr number on Nanofraction Profile |
Figures 10 to 11 depict the effect of Dufour number on temperature and concentration profiles. It is observed that increase in the Dufour number leads to increase in the thermal boundary layer and the concentration boundary layer thickness. 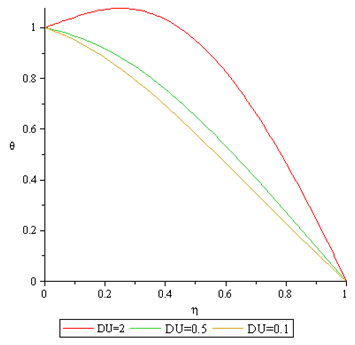 | Figure 10. Effect of DU on Temperature Profile |
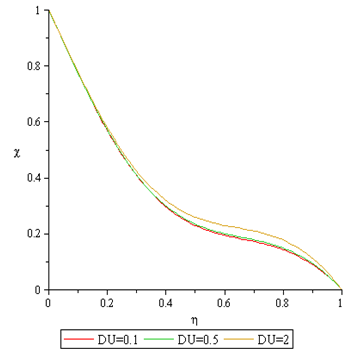 | Figure 11. Effect of DU on Nanofraction Profile |
Figures 12 to 13 show that the fluid temperature and concentration respectively attains their maximum value at the moving plate surface and decreases monotonically to free stream zero value away from the plate satisfying the boundary conditions. It is observe that increase in radiation (Ra) causes both the temperature and concentration profiles to increase. 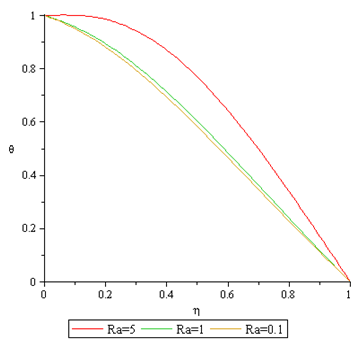 | Figure 12. Effect of Ra on Temperature Profile |
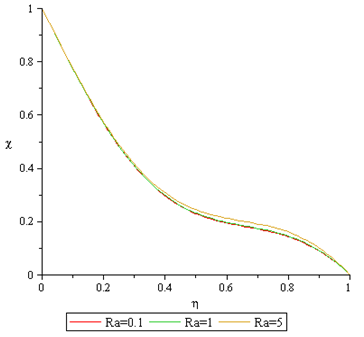 | Figure 13. Effect of Ra on Nanofraction Profile |
Figures 14 to 15 present the effect of Lewis number (Le) on both the temperature and the concentration profiles respectively. It is observe that increase in Lewis number causes the both the temperature and concentration profiles to reduce.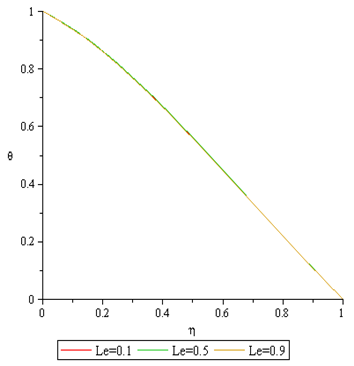 | Figure 14. Effect of Le on Temperature Profile |
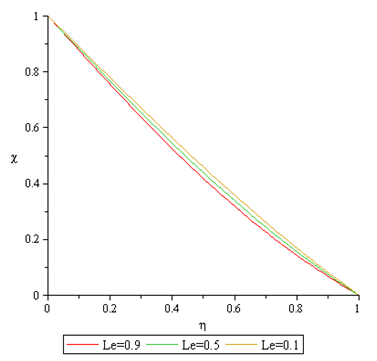 | Figure 15. Effect of Le on Nanofraction Profile |
Figures 16 to 17 display the effect of Soret number (Sr), and it is observe that, increase in the Soret number causes the temperature and nanofraction boundary thickness to reduce.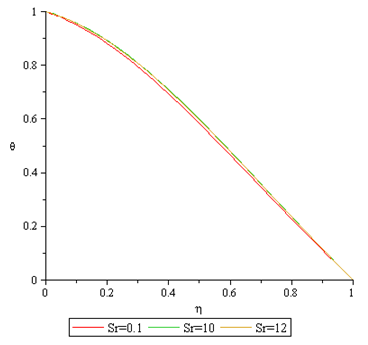 | Figure 16. Effect of the Sr on Temperature Profile |
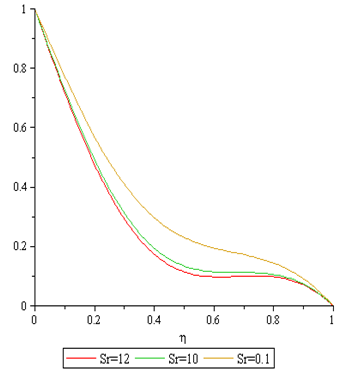 | Figure 17. Effect of the Sr on Nanofraction Profile |
Figures 18 to 19 shows that Brownian motion 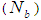 causes the temperature profile and the nanofraction profile to be enhance.
causes the temperature profile and the nanofraction profile to be enhance.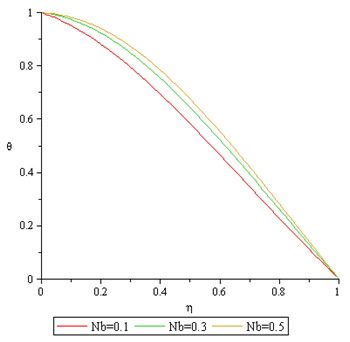 | Figure 18. Effect of Nb on Temperature Profile |
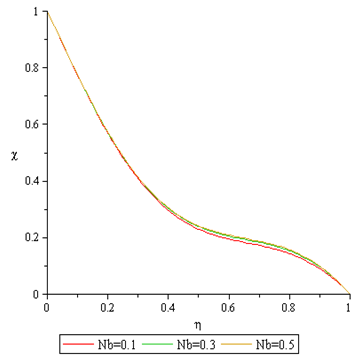 | Figure 19. Effect of Nb on Nanofraction Profile |
Figures 20 to 21 shows that increase in Thermophoresis parameter 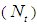 causes the temperature profile to be enhance while the concentration profile reduces.
causes the temperature profile to be enhance while the concentration profile reduces.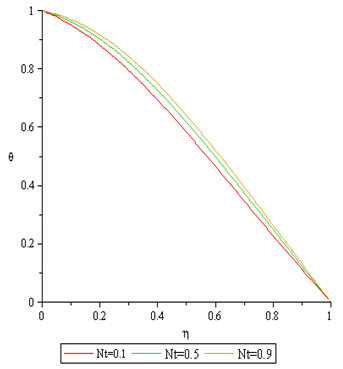 | Figure 20. Effect of Nt on Temperature Profile |
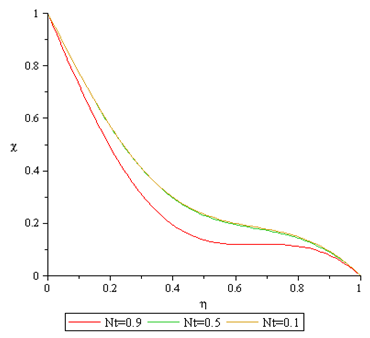 | Figure 21. Effect of Nt on Nanofraction Profile |
4. Conclusions
The solution to the problem of laminar fluid flow in an inclined parallel walls resulting from the movement of the lower wall while the upper wall remain stationary (Coette flow) in a nanofluid with thermal convection, Soret and Dufour effects with radiation has been obtained using the Modified Adomian Decomposition Method for the first time. The model used for the nanofluid was presented in its rectangular coordinate system and incorporates the effect of Brownian motion, and thermophoresis parameter. A similarity solution was presented which depends on the Prandtl number 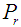 , Lewis number
, Lewis number 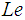 , Brownian motion
, Brownian motion 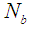 , thermophoresis number
, thermophoresis number 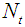 , Soret (Sr) number, Dufour (DU) number, Schimidt number
, Soret (Sr) number, Dufour (DU) number, Schimidt number 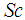 , and Grashof numbers GrT, Grc . It was found that:- 1. All the graphs presented in this work satisfy the boundary conditions.2. It is an established that Soret and Dufour are opposite of one another and this work shows that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. 3. The results obtained in this work are in good agreement with the Numerical Methods as shown in Table 1 which proves the efficiency of the method. 4. Larger values of Prandtl number are equivalent to increase in the thermal conductivity of the fluid and therefore heat is able to diffuse away from the heated surface more rapidly for smaller values of Prandtl number. Hence there is a reduction in temperature with decrease in the Prandtl number.5. It is generally observed from the graphs, that the velocity, temperature and nanofraction profile are at the maximum on the lower channel (moving wall) while they are at minimum on the upper channel (stationary wall). These clearly represent the idea of the authors from the model formulation (realistic). 6. It is also observed in Figure 5 that the higher the Nanofraction Grashof number, the higher the velocity of the fluid at the lower channel; But falls quickly to zero as it approaches the upper wall than for smaller values of nanofraction Grashof number. 7. It should be noted that as a particular quantity is varied, all others are kept constant.
, and Grashof numbers GrT, Grc . It was found that:- 1. All the graphs presented in this work satisfy the boundary conditions.2. It is an established that Soret and Dufour are opposite of one another and this work shows that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. 3. The results obtained in this work are in good agreement with the Numerical Methods as shown in Table 1 which proves the efficiency of the method. 4. Larger values of Prandtl number are equivalent to increase in the thermal conductivity of the fluid and therefore heat is able to diffuse away from the heated surface more rapidly for smaller values of Prandtl number. Hence there is a reduction in temperature with decrease in the Prandtl number.5. It is generally observed from the graphs, that the velocity, temperature and nanofraction profile are at the maximum on the lower channel (moving wall) while they are at minimum on the upper channel (stationary wall). These clearly represent the idea of the authors from the model formulation (realistic). 6. It is also observed in Figure 5 that the higher the Nanofraction Grashof number, the higher the velocity of the fluid at the lower channel; But falls quickly to zero as it approaches the upper wall than for smaller values of nanofraction Grashof number. 7. It should be noted that as a particular quantity is varied, all others are kept constant.
References
| [1] | E. Abu-Nada, Z. Masoud, A. Hijazi (2008). Natural convection heat transfer enhancement in horizontal concentric annuli using nanofluids, Int. Commun. Heat Mass Transfer 35, 657–665. |
| [2] | R. Ellahi (2013). The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: analytical solutions, Appl. Math. Modell. 37 (3), 1451–1467. |
| [3] | M. Sheikholeslami, M. Gorji-Bandpy, D.D. Ganji (2013). Numerical investigation of MHD effects on Al2O3–water nanofluid flow and heat transfer in a semiannulus enclosure using LBM, Energy 60 501–510. |
| [4] | M.M. Rashidi, S. Abelman, N. Freidooni Mehr (2013). Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid, Int. J. Heat Mass Transfer 62, 515–525. |
| [5] | M. Sheikholeslami, M. Gorji-Bandpy, S. Soleimani (2013). Two phase simulation of nanofluid flow and heat transfer using heatline analysis, Int. Commun. Heat Mass Transfer 47, 73–81. |
| [6] | M. Sheikholeslami, M. Gorji-Bandpy, R. Ellahi, A. Zeeshan (2014). Simulation of MHD CuO–water nanofluid flow and convective heat transfer considering Lorentz forces, J. Mag. Magn. Mater. 369, 69–80. |
| [7] | A.Sh. Kherbeet, H.A. Mohammed, B.H. Salman (2012). The effect of nanofluids flow on mixed convection heat transfer over microscale backward-facing step, Int. J. Heat Mass Transfer 55, 5870–5881. |
| [8] | Aiyesimi, Y.M., Yusuf, A., Jiya, M. (2015). Hydromagnetic Boudary-Layer Flow of a Nanofluid Past a Stretching Sheet Embedded in a Darcian Porous Medium with Radiation. Nigerian Journal of Mathematics and Applications, 24, 13-29. |
| [9] | Aiyesimi, Y.M. Yusuf, A. & Jiya, M. (2015). An Analytic Investigation Of Convective Boundary-Layer Flow Of A Nanofluid Past A Stretching Sheet With Radiation. Journal of Nigerian Association of Mathematical Physics. 29 (1), 477-490. |
| [10] | Khan, W.A., Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet, Int. J. Heat Mass Transf. 53, 2477-2483 (2010). S. M. Metev and V. P. Veiko, Laser Assisted Microtechnology, 2nd ed., R. M. Osgood, Jr., Ed. Berlin, Germany: Springer-Verlag, 1998. |
| [11] | Sheikholeslami, M., Abelman, S., Ganji, D. D. (2014). Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. International Journal of Heat and Mass Transfer 79, 212–222. |
| [12] | Ebaid, A. & Al-Armani, N. (2013). A new Approach for a Class of the Blasius Problem via a Transformation and Adomian’s Method. Abstract and Applied Analysis, the Scientific World Journal, 2013. |


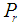 , Lewis number
, Lewis number 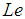 , Brownian motion
, Brownian motion 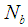 , thermophoresis number
, thermophoresis number 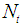 , Soret (Sr) number, Dufour (DU) number, and Grashof numbers GrT, Grc. It is found that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. A comparative analysis of present study was carried out with the numerical on Table 1, and it was observed the two method are in good agreement.
, Soret (Sr) number, Dufour (DU) number, and Grashof numbers GrT, Grc. It is found that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. A comparative analysis of present study was carried out with the numerical on Table 1, and it was observed the two method are in good agreement.
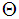 is considered. It is assumed that the wall located at
is considered. It is assumed that the wall located at 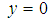 stretches with a velocity
stretches with a velocity 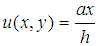 (couette flow), while the other wall at
(couette flow), while the other wall at 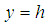 (h = is the width of the channel) remain stationary throughout the flow, where a is constant and
(h = is the width of the channel) remain stationary throughout the flow, where a is constant and 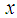 is the coordinate measured along the stretching wall. The temperature
is the coordinate measured along the stretching wall. The temperature 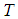 and the nanoparticle fraction
and the nanoparticle fraction 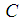 have constants values
have constants values 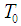 and
and 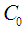 at
at 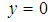 and
and 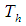 and
and 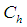 at
at 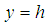 respectively. For this application, we will adopt the natural convection with Soret, Dufour, and Radiation effects for the formulation of Khan and Pop [10] and it is governed by the following equations:Continuity equation:
respectively. For this application, we will adopt the natural convection with Soret, Dufour, and Radiation effects for the formulation of Khan and Pop [10] and it is governed by the following equations:Continuity equation: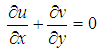
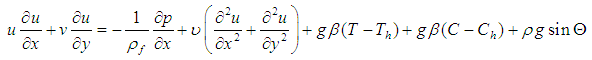
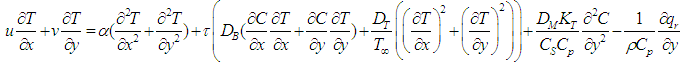
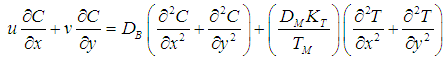
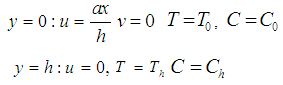
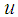 and
and 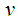 are the velocity components along the
are the velocity components along the 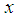 and
and 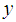 axes respectively,
axes respectively, 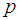 is the fluid pressure,
is the fluid pressure, 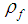 is the density of the base fluid,
is the density of the base fluid, 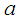 is the thermal diffusivity,
is the thermal diffusivity, 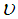 is the kinematic viscousity,
is the kinematic viscousity, 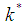 is the thermal conductivity,
is the thermal conductivity, 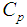 is the specific heat capacity at constant pressure,
is the specific heat capacity at constant pressure, 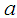 is a positive constant,
is a positive constant, 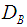 is the Brownian diffusion coefficient,
is the Brownian diffusion coefficient, 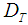 is the thermopheric diffusion coefficient and
is the thermopheric diffusion coefficient and 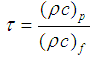 is the ratio between the effective heat capacity of the fluid with
is the ratio between the effective heat capacity of the fluid with 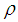 being the density,
being the density, 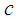 is the volumetric volume expansion coefficient and
is the volumetric volume expansion coefficient and 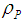 is the density of the particles g is the acceleration due to gravity,
is the density of the particles g is the acceleration due to gravity, 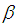 is the volumetric coefficient of thermal expansion,
is the volumetric coefficient of thermal expansion, 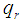 is the radiative heat flux
is the radiative heat flux 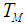 is the mean fluid temperature,
is the mean fluid temperature, 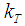 is the thermal diffusion ratio,
is the thermal diffusion ratio, 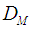 is the diffusion ratio,
is the diffusion ratio, 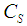 is concentration susceptibility.Following Roseland approximation we have
is concentration susceptibility.Following Roseland approximation we have 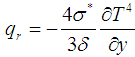 , where
, where 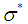 and
and 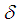 are the Stefan-Boltzmann constant and the mean absorption coefficient respectively. The temperature differences within the fluid is assumed sufficiently small such that
are the Stefan-Boltzmann constant and the mean absorption coefficient respectively. The temperature differences within the fluid is assumed sufficiently small such that 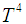 may be expressed as a linear function of Temperature. Expanding
may be expressed as a linear function of Temperature. Expanding 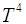 in Taylor’s series about
in Taylor’s series about 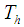 and neglecting higher order terms, we get
and neglecting higher order terms, we get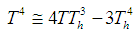
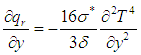 , Defining the dimensional stream function
, Defining the dimensional stream function 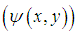 in the usual way such that
in the usual way such that 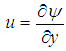 and
and 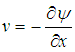 and following the work of Sheikholeslami [11] :-
and following the work of Sheikholeslami [11] :-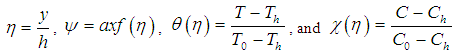
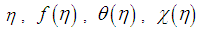 are the dimensionless fluid distance, velocity profile, temperature profile, and nanoparticle concentration.Neglecting the pressure gradient equations (1) to (6) reduces to the following local similarity solution:-
are the dimensionless fluid distance, velocity profile, temperature profile, and nanoparticle concentration.Neglecting the pressure gradient equations (1) to (6) reduces to the following local similarity solution:- 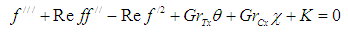
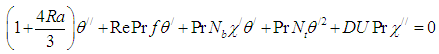
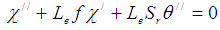
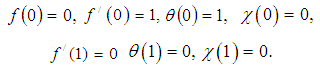
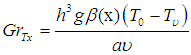 ,
, 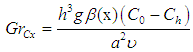 ,
, 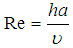 ,
, 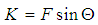
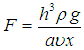 ,
, 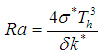 ,
, 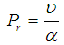
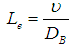 ,
, 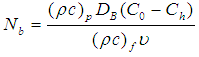
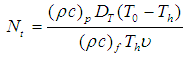
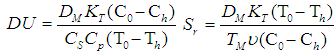 are the local Thermal Grashof number, local concentration Grashof number, Renold number, Gravitational parameter, Radiation, Prandtl number, Lewis number, Brownian motion parameter, thermophoresis parameter, Dufour number, Soret number, and Schmidt number, respectively. For the momentum equation to have a similarity solution, the parameters
are the local Thermal Grashof number, local concentration Grashof number, Renold number, Gravitational parameter, Radiation, Prandtl number, Lewis number, Brownian motion parameter, thermophoresis parameter, Dufour number, Soret number, and Schmidt number, respectively. For the momentum equation to have a similarity solution, the parameters 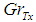 and
and 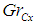 most be constant and not functions of
most be constant and not functions of 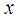 . This can be met if volumetric coefficient of thermal expansion
. This can be met if volumetric coefficient of thermal expansion 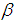 is proportional to
is proportional to 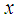 . We therefore assume
. We therefore assume 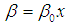
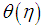 for different values of
for different values of 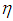 at
at 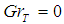 and
and 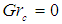 with the Numerical method as shown in Table 1. It was observed that the present method is in good agreement with the Numerical-Method.
with the Numerical method as shown in Table 1. It was observed that the present method is in good agreement with the Numerical-Method.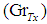 on the velocity profile, temperature and concentration profile and nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile and the nanofraction profile while the temperature profile reduces as the thermal Grashof number increases.
on the velocity profile, temperature and concentration profile and nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile and the nanofraction profile while the temperature profile reduces as the thermal Grashof number increases. 
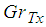 on Velocity Profile
on Velocity Profile
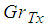 on Temperature Profile
on Temperature Profile
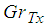 on Nanofraction Profile
on Nanofraction Profile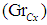 . On the velocity profile, temperature and Nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile at the lower wall (moving wall), where the fluid velocity is maximum and decreases the velocity profile faster for higher values of Concentration profile at the upper wall (stationary wall), where the flow velocity is minimum. The temperature profile and the nanofraction profiles are enhanced. This leads to increase in the boundary layers as shown in the graph.
. On the velocity profile, temperature and Nanofraction profile. It is observed that the thermal Grashof number enhances the velocity profile at the lower wall (moving wall), where the fluid velocity is maximum and decreases the velocity profile faster for higher values of Concentration profile at the upper wall (stationary wall), where the flow velocity is minimum. The temperature profile and the nanofraction profiles are enhanced. This leads to increase in the boundary layers as shown in the graph.
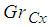 on Velocity Profile
on Velocity Profile
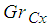 on Temperature Profile
on Temperature Profile
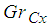 on Nanofraction Profile
on Nanofraction Profile









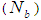 causes the temperature profile and the nanofraction profile to be enhance.
causes the temperature profile and the nanofraction profile to be enhance.

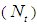 causes the temperature profile to be enhance while the concentration profile reduces.
causes the temperature profile to be enhance while the concentration profile reduces.

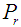 , Lewis number
, Lewis number 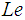 , Brownian motion
, Brownian motion 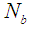 , thermophoresis number
, thermophoresis number 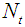 , Soret (Sr) number, Dufour (DU) number, Schimidt number
, Soret (Sr) number, Dufour (DU) number, Schimidt number 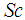 , and Grashof numbers GrT, Grc . It was found that:- 1. All the graphs presented in this work satisfy the boundary conditions.2. It is an established that Soret and Dufour are opposite of one another and this work shows that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. 3. The results obtained in this work are in good agreement with the Numerical Methods as shown in Table 1 which proves the efficiency of the method. 4. Larger values of Prandtl number are equivalent to increase in the thermal conductivity of the fluid and therefore heat is able to diffuse away from the heated surface more rapidly for smaller values of Prandtl number. Hence there is a reduction in temperature with decrease in the Prandtl number.5. It is generally observed from the graphs, that the velocity, temperature and nanofraction profile are at the maximum on the lower channel (moving wall) while they are at minimum on the upper channel (stationary wall). These clearly represent the idea of the authors from the model formulation (realistic). 6. It is also observed in Figure 5 that the higher the Nanofraction Grashof number, the higher the velocity of the fluid at the lower channel; But falls quickly to zero as it approaches the upper wall than for smaller values of nanofraction Grashof number. 7. It should be noted that as a particular quantity is varied, all others are kept constant.
, and Grashof numbers GrT, Grc . It was found that:- 1. All the graphs presented in this work satisfy the boundary conditions.2. It is an established that Soret and Dufour are opposite of one another and this work shows that increase in Soret number leads to reduction in temperature and nanofraction profiles while increase in Dufour number enhances the temperature and nanofracion profiles. 3. The results obtained in this work are in good agreement with the Numerical Methods as shown in Table 1 which proves the efficiency of the method. 4. Larger values of Prandtl number are equivalent to increase in the thermal conductivity of the fluid and therefore heat is able to diffuse away from the heated surface more rapidly for smaller values of Prandtl number. Hence there is a reduction in temperature with decrease in the Prandtl number.5. It is generally observed from the graphs, that the velocity, temperature and nanofraction profile are at the maximum on the lower channel (moving wall) while they are at minimum on the upper channel (stationary wall). These clearly represent the idea of the authors from the model formulation (realistic). 6. It is also observed in Figure 5 that the higher the Nanofraction Grashof number, the higher the velocity of the fluid at the lower channel; But falls quickly to zero as it approaches the upper wall than for smaller values of nanofraction Grashof number. 7. It should be noted that as a particular quantity is varied, all others are kept constant.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML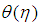 with the present work for
with the present work for