Hajji Tarik
Université Privée de Fès, Lotissement Qaraouiyine, Route d’Ain Chkef, Fès, Maroc
Correspondence to: Hajji Tarik, Université Privée de Fès, Lotissement Qaraouiyine, Route d’Ain Chkef, Fès, Maroc.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Signing digital images is a crucial operation in protecting the integrity of information in a digital image. In this work, we will show how we can use ANN as a agreeable hash function to the digital signature digital image. We will also give a description of an approach to develop a system of signing and verification for digital images using ANN. The objective of this work is not only to demonstrate the use of neural networks for signature but also to look for possible relationships between the rate of similarities images and to derive conditions of use for not collusion identical signatures. The advantages of this new approach are numerous; the shape of the standard signature is of fixed size for all documents, signature did not have kidney with formant data signed image and the signing operation is independent of any key signature. We will start with an introduction to the presentation of the state of the art on this topic. Then we will explain the methodology used to produce the signature system presenting the unsupervised learning algorithm and then we'll figurative results found, interpret and demonstrate this approach and finally we will conclude this study by all the conclusions and prospects for this work.
Keywords:
ANN, Digital Image, Digital Signature, Hashes function
Cite this paper: Hajji Tarik, Signing Digital Images by ANN, American Journal of Computational and Applied Mathematics , Vol. 6 No. 2, 2016, pp. 50-56. doi: 10.5923/j.ajcam.20160602.04.
1. Introduction
The digital signature is an operation that ensures all the documents signed. In other words, the mechanism protects the document against tampering operations and modification at the time of transmission of such documents. We can distinguish between two types of signatures:The digital signature is an operation that ensures all the documents signed. In other words, the mechanism protects the document against falsification and the operations to change the documents at the time of transmission of this document. We can distinguish between two types of signatures:1. The first type is exhibited in the RSA cryptographic scheme [1]. In this method, the signature of a document is another document comparable with the document signed (in this case, you must send two documents: the signed document and the signature of the document). The size of the document signature is a function of the size of the signed document. As we have a characteristic property of such signature is that only subjects can verify the signature because it is them that they have the verification keys.2. The second type of signature is the classical notion of signature, when we have a public signing algorithm (eg a hash function) accessible by everyone. This type does not depend on a key signature, even for the size of the signature is in general independent of the size of the document and the signature is not more than a reduced information amount compared to the signed information.The concept of integrity is a well known concept in security. Its definition is based on a binary decision ensures that the data received are strictly identical to those issued. This definition is applicable to any type of digital documents; however, in practice it turns out to be too strict and inadequate for multimedia documents. Indeed, the interpretation that we have an image depends mainly on the constituent elements rather than the numerical values of pixels or resolution. In other words, the problem of the integrity of images arises primarily in terms of semantic content; that is to say, the detection of document changes can cause discomfort in the viewing and / or erred in its interpretation (modification of the legend, loss of face, etc...). In order to ensure proper integrity service for images, it is important to distinguish malicious manipulations of diverting the original image content; manipulations associated with its use or are stored in digital form (format conversion, compression, resembling, filtering, etc.) made by content providers or users themselves. Unfortunately, this distinction is not always easy for a computer science point of view depends partly on the type of image and its use. For example, in the case of medical imaging, innocuous manipulations, such as simple compression or the tattooing process itself, can cause the disappearance of certain visible signs of pathology while distorting the doctor's diagnosis. In the following non-exhaustive list of the protocols most famous signing is indicated: ü Protocol of signature private keyü Protocol public key signatureü Protocol datingü Protocol public key signature and hash functionA digital image is a function of discrete and bounded support, and discrete values. The support is multidimensional, usually 2D or 3D. Values can be scalar or vector. Gem of possible values varies depending on the type of images considered.
1.1. Hash Functions
A hash function is a quick function to compute but whose inverse image is the class of computationally difficult problems (NP class). It transforms a message of arbitrary length into a hash code or message authentication of fixed size, typically 160 bits currently. For safety reasons there is a tendency to increase the size of the fingerprint. The scheme for calculating a signature using a hash function is as follows: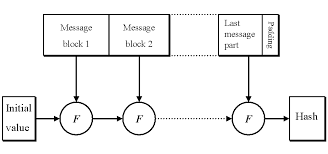 | Figure 1. Operating principle of hash functions |
In reality a hash function takes a message x smaller than N set it into a cavity of size 160 bits (or 256 or 384 or 51. The hash function must be carefully constructed so that it does not weaken the Protocol of Signature. Since a hash function is not injective obviously, there are pairs of messages and x0 x such that h (x0) = h (x). Among the strengths that must verify a hash function is that it must resist the attack anniversaries. The ANN was calculated units not necessarily linear able to build relationships between a field input information reassemble or less than another field output information. This feature allows us to turn off the use of ANN as functions of powerful hashes. The strengths of this use is that ANN are resistible to deferent attack as the attack birthdays or as we demonstrate in the interpretation part. On more than this, we can always fix the size of the output, this property enables us to calculate the probability of collusion on the ANN used as a hash function.
1.2. ANN
The ANN is inspired by biological neural system. It is composed of several interconnected elements to solve a collection of varied problems. The brain is composed of billions of neurons and trillions of connections between them. The nerve impulse travels through the dendrites and axons, and then treated in the neurons through synapses. This results in the field of ANN in several interconnected elements or belonging to one of the three marks neurons, input, output or hidden. Neurons belonging to layer n are considered an automatic threshold. In addition, to be activated, it must receive a signal above this threshold, the output of the neuron after taking into account the weight parameters, supplying all the elements belonging to the layer n+1. As biological neural system, neural networks have the ability to learn, which makes them useful.The ANN are units of troubleshooting, capable of handling fuzzy information in parallel and come out with one or more results representing the postulated solution. The basic unit of a neural network is a non-linear combinational function called artificial neurons. An artificial neuron represents a computer simulation of a biological neuron human brain. Each artificial neuron is characterized by an information vector which is present at the input of the neuron and a non-linear mathematical operator capable of calculating an output on this vector. The following figure shows an artificial neuron [20]: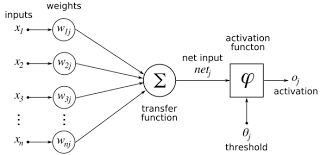 | Figure 2. Artificial neural |
The synapses are Wij (weights) of the J neural; they are real numbers between 0 and 1. The function is a summation of combinations between active synapses associated with the same neuron. The activation function is a non-linear operator to return a true value or rounded in the range [0 1]. In our case we use the sigmoid function [21]: 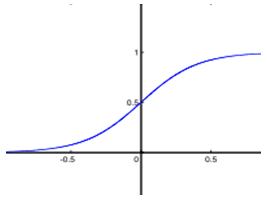 | Figure 3. Sigmoid function |
An ANN is composed by a collection of artificial neurons interconnected among them to form a neuronal system able to learn and to understand the mechanisms. Each ANN is characterized by its specific architecture; this architecture is denoted by the number of neurons of the input layer, the number of hidden layers, the number of neurons in each hidden layer and the neurons number in the output layer. A layer of neurons in a neural network is a group of artificial neurons, with the same level of importance, as is shown in the following figure [22]: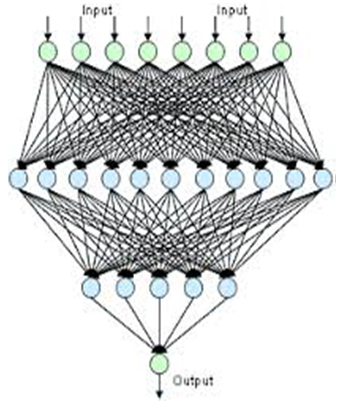 | Figure 4. ANN |
The operating principle of ANN is similar to the human brain; first, it must necessarily pass on the learning phase to record knowledge in the memory of the ANN. The storage of knowledge is the principle of reputation and compensation to a collection of data that forms the basis of learning. We have several algorithms that can teach an ANN as backpropagation. The backpropagation is a method of calculating the weight for network supervised learning is to minimize the squared error output. It involves correcting errors according to the importance of the elements involved in fact the realization of these errors: the synaptic weights that help to generate a significant error will be changed more significantly than the weights that led to a marginal error. In the neural network, weights are, first, initialized with random values. It then considers a set of data that will be used for learning.
1.3. Digital Image Signing Methods
We have a very large collection of methods invented to do the signature of digital images and we can be further subdivided into two types: External signatures provide an alternative to conventional watermarking techniques under service integrity check in the pictures. Unlike image watermarking techniques, the trade mark is not inserted in the image itself, but transmitted with it in an encrypted form. The technique of "row-column hash function" is to calculate a hash value for each row and each column of the original image. When it is desired to check the integrity of an image, it recalculates the hash values of the rows and columns of the image to be tested and compared with those of the original image. Another algorithm also uses hash functions; it is the function Hash Block-Based (BBH). The principle is similar to that described above, except that it no longer operates on the rows or columns of the image, but on blocks. Thus when there are differences in the hash values, simply refer to the relevant blocks to locate areas of the image that has been manipulated [3, 13]. Unlike techniques using hash functions for generating a fingerprint image, some authors, such as Lin and Chang or Queluz offer to extract the intrinsic characteristics of the image, such as edges, and encrypting using an asymmetric encryption algorithm to transmit simultaneously image [15, 16]. In 2014 we established in our laboratory for research in computer Lari, a new approach in an article entitled "Digital Signature images by tattooing and ANN." The principle of this method is to tattoo the image you want to sign the compressed image with an ANN for supervised learning. The advantage of this method is that it provides a very simple and immediate verification mechanism.
2. Methodologie
The aid of this method is to make a simulation between the uses of hash functions for digital signing digital images and ANN. We will work on a test database composed of 1000 images of Linda, each one is slightly modified compared to the others. Bute is to prove experimentally that this system that uses ANN as a method of digital signature images is resistible for months of 1,000 infinitely small changes on a test image. The first step in this process is the creation of a network of artificial neurons characterized by the architecture (64.0, 4). Designates the architecture of a neural network the number of neurons in the input layer, the number of hidden, the number of neurons in each hidden layer and the number of neurons in the output layer of layers. Thus, architecture (64, 0, 4) denotes an ANN 64 characterized by artificial neurons in the input layer in the form of a square matrix of size 8 * 8, and not hidden layer neurons in 4 the output layer form a matrix of size 2 * 2. After the creation and instantiation of this ANN, proceed to the preparation of a collection of images to form the basis of tests of the system signature. This base is formed by 1,000 carefully selected images. As a first step, we will use the neural network directly without learning to the digital signature. Then we will repeat the signing of these images with an ANN previously taught to the signature. The purpose of this database test is not only to demonstrate the use of ANN for the digital signature image but also calculate the probability of collusion: In a space of K images, what is the probability of finding two images with the same signature with ANN.
2.1. Signature Algorithm with ANN
For a digital image gives M; Must subdivide the image into M blocks Mij size 64 = 8 * 8 (a block Mij is a square matrix of size 8 * 8). We near the block size in this case equal to 64 what we have a neural network composed of an input layer formed by 8 * 8 = 64 neurons entries.After, we will propagate the signals for each Mij forward block in the ANN. The forward propagation in the network is done using the following formula Si = sigmoide (sum (Mij(i,j) * Wij); with: Wij have the synaptic weight of the output neuron number i in the ANN. It should be noted that the synaptic weights are initialized randomly at the time of the creation of ANN (one can make a further study for a set of the initialization condition in the synaptic weights for minimizing the response time of the ANN in the case of learning and also to minimize the likelihood of having collusion) Mij is the value of the matrix element of the power input associated with synaptic weight Wij. Thus we have for each image block to sign; it will generate another output block size of 2 * 2. After passing through all the blocks of the image to sign there will be a single output block composed by the output blocks for each block of the image. If this final block is greater than 64 * 64, must repeat the same procedure on the block as the image signature. The final result of the signature is an array of 16 * 16 elements. Example of digital signature for image Linda with ANN without learning: | Figure 5. Image of Linda has signed with ANN |
The following matrix represents an extract of the image signature:  The signature of the image is in the form of a square matrix of 256 real numbers. The implementation of the algorithm in Java can be made by the following recursive function:
The signature of the image is in the form of a square matrix of 256 real numbers. The implementation of the algorithm in Java can be made by the following recursive function:  The following code shows an example of using this function:
The following code shows an example of using this function: We developed TaritementDeImag class to group all the functions that can be done on a digital image such as the extraction of blocks of the image. We used mainly two types of ANN: a- The first layer I (no hidden layer) composed solely by the input layer with 64 artificial neural and with an output layer of 4 artificial neural.
We developed TaritementDeImag class to group all the functions that can be done on a digital image such as the extraction of blocks of the image. We used mainly two types of ANN: a- The first layer I (no hidden layer) composed solely by the input layer with 64 artificial neural and with an output layer of 4 artificial neural. 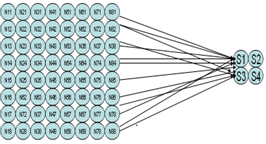 | Figure 6. ANN (64, 4) |
b- The second is a multi layer, it is composed of an input layer always composed by 64 artificial neural, a hidden layer composed by 16 artificial neural and an output layer consisting of 4 artificial neural: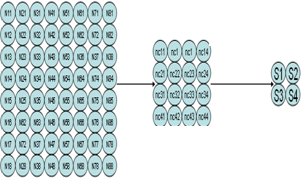 | Figure 7. ANN architecture (64, 16, 4) |
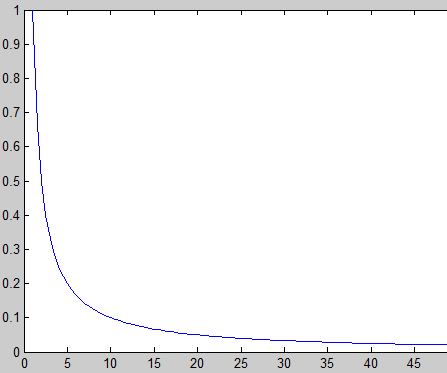 | Figure 8. Convergence of the ANN based on the number of iteration |
We used this last ANN in two modes; no first and second learning with unsupervised learning. The goal of learning in this case is to have a rate of similarity of signatures for a very low rate of similarity of strong images. The idea of the algorithm is to use the principle of correcting the square error of the artificial neural component ANN based on the rate of similarity signatures and images. For example; for an image A, AC SA signed by the ANN with a simple spread of reports of network layers are calculated. Then again calculates the SB signature for another image B such that the degree of similarity of A and B is very strong. After calculating the rate of similarity AND SA and SB and a comparison is made between the rate of the minimum similarity accepted signing SC. If ST < SC then you must correct the error of the neural network with a simple retro propagation of signals back, then the weights of neural network was put openwork. Otherwise we go to treat other images in the training set. The algorithm stop after checking this condition: (ST > SC). The following graph shows the evolution of the convergence of the ANN based on the number of iteration algorithm:
3. Results
Before presenting the results found by the two ANN defined above, we will define all Abor a new concept that will appoint rate of similarity of two images:
3.1. The Rate of Similarity of Two Images
The rate of similarity of two images is no breaking of sizes, but the rate of similarity of two images of the same size is defined by the following relationship: equal number of pixels between the two images divided by the total number of pixels of an image. It may be noted, for example, the rate of similarity between the two images and M1 M2 T (M1, M2). We have the following two statements: T (M1, M2) = 0 è M1 # M2 (the reverse is not true) T (M1, M2) = 1 è M1 = M2: If we consider the following two images M1 and M2: | Figure 9. Image M1 |
 | Figure 10. Image M2 |
(M2 is nothing other than the M1 image with 15 * 15 * 4 pixels of deference)We have in this example, the size of M1 is equal to the size of M2. And we also have 15 * 15 pixels and deferent M2 M1 M1 M2 and size is 225 * 225, where the rate of similarity between M1 and M2: T (M1, M2) = [(225 * 255) - (15 * 15 * 4)] / 225 * 225 = 49725/50625 = 98.2%.
3.2. The Rate of Similarity of Two Signatures
The shape of the signature of a generated by the ANN digital image is a square matrix of size 64 * 64, it is composed by 256 real numbers. The purpose of this choice is to minimize the likelihood of collusion signatures. We can define the rate of similarity of two signatures of the same manuaire the rate of similarity of the images by the relationship changed following: sum (mij - I ij) * (mij - I ij) / 256. The following table contains the results of operations of digital signatures for images in the rate of similarity between these images with an ANN architecture mono layer (64, 4):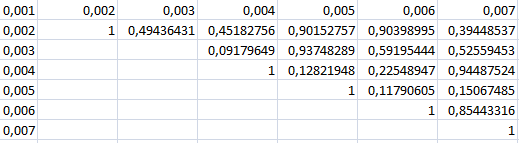 | Figure 11. Results of operations of digital signatures for images in the rate of similarity with a neural network architecture mono layer (64, 4) |
The value of a cell in the table represents the rate of similarity between two corresponding line images and column. This table or that an extract of the results matrix composed by 100 and 1000 lines stick. It should be noted that the construction of this matrix is an automatic manuaire using a java program that takes as input the folder that contains the test images. They put the pair in each cell (T_R_I, T_R_S) respectively to mention (the rate of similarity of images, the rate of similarity signatures). The T_R_I and T_R_S defined both the relations between two images. The following graph shows the relationship between the similarity rates based on signatures similarity rate digital images: | Figure 12. Relationship between the rate of similarity of signatures and the rate of similarity of digital images |
This graph is almost random and it is not linear although the rate of similarity between images is unrigging 0001. The following table contains the results of operations of digital signatures for images in the rate of similarity between these images with an ANN multilayer architecture (64, 16, 4) with an unsupervised learning: | Figure 13. Results of operations of digital signatures for images in the rate of similarity with a ANN multi-layer architecture (64, 16, 4) with an unsupervised learning |
The following graph shows the relationship between the similarity rates based on signatures similarity rate digital images: | Figure 14. Relationship between signing similarity rate and images similarity rate |
The immediate conclusion we can conclude from this figure is that there is no relationship between the rate of similarity of images and signatures.
4. Discussion and Conclusions
In the case of using a network of artificial neurons my layer, in general we have no relationship between the image and signature similarity rate. The conclusion one can have is that the ANN monolayer gives vas signatures very similar images. In the case of using an ANN with multi-layer unsupervised learning we also have different signatures for very similar pictures and in addition we have a very high level of deference that the use of a single layer neural network without learning. The use of ANN as hash functions for the digital signature images offer a new approach to protect the integrity of images. Also this function is a hash function of one-way and high collusion difficult. Among the advantages of this approach that uses ANN; the signature of an image is encoded in a space of fixed size (matrix size 64). The signing process is independent of any key signature; it is fair to master to hasten the network of artificial neurons used to. As a first perspective of this work, we will try to sign the compressed image generated by an ANN, instead of reacting directly on the original image. And among the prospect of work, we will seek the possibility of breaking this method use learning another ANN deferring to that used for the signature. As postulated to make a comparative study of the structures of ANN and the rate of similarity of signatures.
References
| [1] | C. Rey & J.-L. Dugelay. Blind Detection of Malicious Alterations On Still Images Using Robust Watermarks. IEE Secure Images and Image Authentication colloquium, London, UK, Apr. 2000. |
| [2] | M. Kutter, S. Voloshynocskiy and A. Herrigel. The Watermark Copy Attack. In Proceedings of SPIE Security and Watermarking of Multimedia Content II , vol. 3971, San Jose, USA, Jan. 2000. |
| [3] | J. Fridrich, M. Goljan & N. Memon. Further Attacks on Yeung-Minzer Fragile Watermarking Scheme. SPIE International Conf. on Security and Watermarking of Multimedia Contents II , vol. 3971, No13, San Jose, USA, Jan. 2000. |
| [4] | Julien Chable. Emmanuel Robles Programmation Android, de la conception au déploiement avec le SDK Google Android, New York, France, 2009. |
| [5] | S. Bhattacharjee and M. Kutter. Compression Tolerant Image Authentication. IEEE International Conf. on Image Processing (ICIP’98), Chicago, USA, Oct. 1998. |
| [6] | J.-L. Dugelay & S. Roche. Introduction au tatouage d’images. Annales des Télécommunications, 54, no 9-10, pp. 427-437, 1999. |
| [7] | J.-L. Dugelay. Procédé de dissimulation d'informations dans une image numérique. Brevet INPI FR 98-04083 (EURECOM 09-FR), March 1998. |
| [8] | J.-L. Dugelay & S. Roche. Process for marking a multimedia document, such an image, by generating a mark. Pending patent EP 99480075.3 (EURECOM 11/12 EP), July 1999. |
| [9] | J. Fridrich. Robust Bit Extraction From Images. ICMCS’99, Florence, Italy, june 1999. |
| [10] | J. Fridrich and M. Goljan. Protection of Digital Images using Self Embedding. The Symposium on Content Security and Data Hiding in Digital Media, New Jersey Institute of Technology, Mar. 1999. |
| [11] | J. Fridrich. Image Watermarking for Tamper Detection. Proceedings IEEE Int. Conf. on Image Processing (ICIP’98), Chicago, USA, Oct. 1998. |
| [12] | J. Fridrich. Methods for detecting changes in digital images. Proceedings IEEE Int. Conf. On Image Processing (ICIP’98), Chicago, USA, Oct. 1998. |
| [13] | Kodak. Understanding and Intergrating KODAK Picture Authentication Cameras. http://www.kodak.com/US/en/digital/software/imageAuthentication/. |
| [14] | D. Kundur and D. Hatzinakos. Towards a Telltale Watermarking Technique for Tamper-Proofing. IEEE International Conf. on Image Processing (ICIP’98), Chicago, USA, Oct. 1998. |








 The signature of the image is in the form of a square matrix of 256 real numbers. The implementation of the algorithm in Java can be made by the following recursive function:
The signature of the image is in the form of a square matrix of 256 real numbers. The implementation of the algorithm in Java can be made by the following recursive function:  The following code shows an example of using this function:
The following code shows an example of using this function: We developed TaritementDeImag class to group all the functions that can be done on a digital image such as the extraction of blocks of the image. We used mainly two types of ANN: a- The first layer I (no hidden layer) composed solely by the input layer with 64 artificial neural and with an output layer of 4 artificial neural.
We developed TaritementDeImag class to group all the functions that can be done on a digital image such as the extraction of blocks of the image. We used mainly two types of ANN: a- The first layer I (no hidden layer) composed solely by the input layer with 64 artificial neural and with an output layer of 4 artificial neural. 








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML