Olabode B. T., Momoh A. L.
Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria
Correspondence to: Olabode B. T., Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This article proposed continuous hybrid multistep methods with Legendre polynomial as basis functions for the direct solution of system of second order ordinary differential equations. This was achieved by constructing a continuous representation of hybrid multistep schemes via interpolation of the approximate solution and collocation of derivative function with Legendre polynomial as basis functions. The discrete schemes were obtained from the continuous scheme as a by-product and applied in block form as simultaneous numerical integrators to solve initial value problems (IVPs). The resultant schemes are self-starting, do not need the development of separate predictors, consistent, zero-stable and convergent. The performance of the methods was demonstrated on some numerical examples to show accuracy and efficiency advantages. The numerical results compared favourably with existing method.
Keywords:
Continuous, Hybrid, Multistep method, Legendre polynomial, Stiff equations, Initial Value Problems (IVPs), Ordinary Differential Equations (ODEs)
Cite this paper: Olabode B. T., Momoh A. L., Continuous Hybrid Multistep Methods with Legendre Basis Function for Direct Treatment of Second Order Stiff ODEs, American Journal of Computational and Applied Mathematics , Vol. 6 No. 2, 2016, pp. 38-49. doi: 10.5923/j.ajcam.20160602.03.
1. Introduction
The mathematical modeling of physical phenomena in science and engineering field especially in mechanical systems with several springs attached in series or dissipation, control theory, celestial mechanics, series circuits lead to a system of differential equations (see Landau and Lifshitz (1965), Liboff (1980)). Realistically, the analytical solutions of most differential equations are not easily obtainable. This necessitated the need for approximate solution by the application of numerical techniques. The techniques for the derivation of continuous linear multistep methods (LMMs) for direct solution of initial value problems in ordinary differential equations have been discussed in literature over the years and these include, among others collocation, interpolation, integration and interpolation polynomials. Basis functions such as, power series, Chebyshev polynomials, trigonometric functions, the monomials 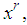 the canonical polynomial
the canonical polynomial 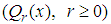 of the Lanczos Tau method in a perturbed collocation approach have been employed for this purpose (see Abualnaja (2015); Adeyefa et al., (2014); Awoyemi and Idowu (2005); Lambert (1991)).Moreover, power series has also being extensively used in literature for the same purpose. Sirisena et al., (2004) proposed a new Butcher type two-step block hybrid multistep method for accurate and efficient parallel solution of order ordinary differential equations. Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third order ordinary differential equations with power series as the basis functions and were implemented in predictor –corrector mode. Ehigie et al., (2010) worked on generalized two-step continuous linear multistep method of hybrid type for the direct integration of second order ordinary differential equations. Fudzial et al., (2009) constructed the explicit and implicit 3-point-1- block (I3P1B) for solving special second order ordinary equations directly. Awari (2013) considered the derivation and application of six-point linear multistep numerical method for the solution of second order initial value problems which was implemented in block mode. Yusuph and Onumanyi (2002) demonstrated a successful application of multiple finite difference methods through multistep collocation for the second order ordinary differential equations. Furthermore, Abualnaja (2015) constructed a block procedure with linear multistep methods using Legendre polynomial for solving first order ordinary differential equations. The method depends on the perturbed collocation approximation with Legendre as perturbation term for the solution of first order ordinary differential equations. In the work of Yakusak et al., (2015), uniform order Legendre approach for continuous hybrid block methods were proposed for the solution of first order ordinary differential equations. In this paper, we propose the choice of Legendre polynomial without perturbation as basis functions for the construction of continuous schemes, which simultaneously generate solution of (1). They are self-starting and do not need any predictors. PreliminariesA central notion in this work concerns the choice of Legendre polynomial as basis functions in the derivation of the continuous schemes, the implementation strategies employed (in block mode) and the stability analysis of the methods. For convenience of the reader, we recall the definitions as follows:Definition 1.1: The block method is said to be zero-stable if the roots
of the Lanczos Tau method in a perturbed collocation approach have been employed for this purpose (see Abualnaja (2015); Adeyefa et al., (2014); Awoyemi and Idowu (2005); Lambert (1991)).Moreover, power series has also being extensively used in literature for the same purpose. Sirisena et al., (2004) proposed a new Butcher type two-step block hybrid multistep method for accurate and efficient parallel solution of order ordinary differential equations. Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third order ordinary differential equations with power series as the basis functions and were implemented in predictor –corrector mode. Ehigie et al., (2010) worked on generalized two-step continuous linear multistep method of hybrid type for the direct integration of second order ordinary differential equations. Fudzial et al., (2009) constructed the explicit and implicit 3-point-1- block (I3P1B) for solving special second order ordinary equations directly. Awari (2013) considered the derivation and application of six-point linear multistep numerical method for the solution of second order initial value problems which was implemented in block mode. Yusuph and Onumanyi (2002) demonstrated a successful application of multiple finite difference methods through multistep collocation for the second order ordinary differential equations. Furthermore, Abualnaja (2015) constructed a block procedure with linear multistep methods using Legendre polynomial for solving first order ordinary differential equations. The method depends on the perturbed collocation approximation with Legendre as perturbation term for the solution of first order ordinary differential equations. In the work of Yakusak et al., (2015), uniform order Legendre approach for continuous hybrid block methods were proposed for the solution of first order ordinary differential equations. In this paper, we propose the choice of Legendre polynomial without perturbation as basis functions for the construction of continuous schemes, which simultaneously generate solution of (1). They are self-starting and do not need any predictors. PreliminariesA central notion in this work concerns the choice of Legendre polynomial as basis functions in the derivation of the continuous schemes, the implementation strategies employed (in block mode) and the stability analysis of the methods. For convenience of the reader, we recall the definitions as follows:Definition 1.1: The block method is said to be zero-stable if the roots 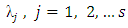 of the characteristic polynomial
of the characteristic polynomial 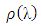 defined by
defined by 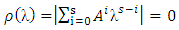 satisfies
satisfies 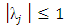 and for those roots with
and for those roots with 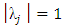 , the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals
, the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals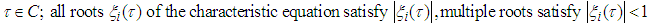 is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition: 1.3 (Widlund (1967))A method is said to be A(α)-stable if the sector
is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition: 1.3 (Widlund (1967))A method is said to be A(α)-stable if the sector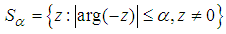 is contained in the stability region.Definition 1.4 (Ehle (1969)): A method is called L-stable if it is A-stable and if in addition
is contained in the stability region.Definition 1.4 (Ehle (1969)): A method is called L-stable if it is A-stable and if in addition 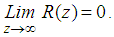 Definition 1.5 (Olagunju et al., (2012)): Legendre polynomial is special case of the Legendre function which satisfy the differential equation
Definition 1.5 (Olagunju et al., (2012)): Legendre polynomial is special case of the Legendre function which satisfy the differential equation 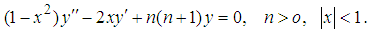 The general solution can be expressed as:
The general solution can be expressed as: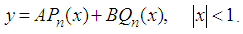
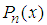 and
and 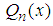 are respectively the Legendre functions of the first-and second-kind of the order n. The nth order polynomial
are respectively the Legendre functions of the first-and second-kind of the order n. The nth order polynomial 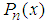 is generally given by the following equation:
is generally given by the following equation: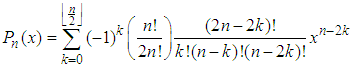 where n is the order of the Legendre polynomials,
where n is the order of the Legendre polynomials, 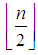 signifies the integer part of
signifies the integer part of 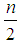 . Legendre polynomials are orthogonal to each other with respect to weight function w(x) = 1 on [-1,1]. The first two polynomials are always the same in all cases but the higher orders are created with recursive formula:
. Legendre polynomials are orthogonal to each other with respect to weight function w(x) = 1 on [-1,1]. The first two polynomials are always the same in all cases but the higher orders are created with recursive formula: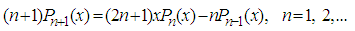 with initial conditions:
with initial conditions: 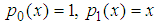 . The first four terms of the polynomial are;
. The first four terms of the polynomial are; 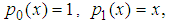
 The paper is organized as follows. Section 1 is of an introductory nature. The materials and methods are described in Section 2. Stability analysis of the methods is discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.
The paper is organized as follows. Section 1 is of an introductory nature. The materials and methods are described in Section 2. Stability analysis of the methods is discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.
2. Mathematical Formulation
Consider the second-order initial value problem: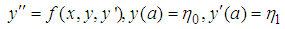 | (1) |
where 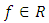 is sufficiently differentiable and satisfies a Lipschitz condition, sufficiently smooth,
is sufficiently differentiable and satisfies a Lipschitz condition, sufficiently smooth, 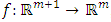 , y is an m-dimensional vector and
, y is an m-dimensional vector and 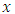 is a scalar variable and a set of equally spaced points on the integration interval also given by
is a scalar variable and a set of equally spaced points on the integration interval also given by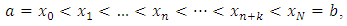 | (2) |
with a specified positive integer step number k greater than zero, h can be variable or constant step-size given by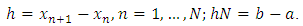 Assuming an approximate solution to (1) by taking the partial sum of Legendre polynomial of the form:
Assuming an approximate solution to (1) by taking the partial sum of Legendre polynomial of the form: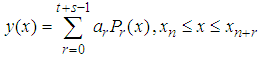 | (3) |
where can be used only after certain transformation. The second derivative of (3) gives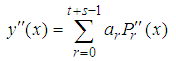 | (4) |
Substituting (4) into (1) gives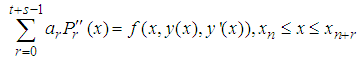 | (5) |
where 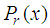 is the Legendre polynomial of degree
is the Legendre polynomial of degree 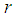 , valid in
, valid in 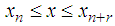 and
and 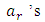 are real unknown parameters to be determined and
are real unknown parameters to be determined and 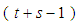 is the sum number of collocation and interpolation points. The well-known Legendre polynomials are defined on the interval [-1,1].
is the sum number of collocation and interpolation points. The well-known Legendre polynomials are defined on the interval [-1,1].
2.1. Derivation of the Continuous Hybrid Multistep Methods
Our objective here is to construct a continuous formulation of the general linear multistep method 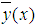 of degree
of degree 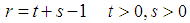 . Two cases were considered one-step and two-step methods.CASE 1: One-Step Continuous Hybrid Multistep Method (OSCHMM).Collocating (5) at points, and interpolating (3) at points
. Two cases were considered one-step and two-step methods.CASE 1: One-Step Continuous Hybrid Multistep Method (OSCHMM).Collocating (5) at points, and interpolating (3) at points 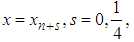 respectively lead to a system of equations expressed in matrix form:
respectively lead to a system of equations expressed in matrix form: 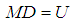 | (6) |
where,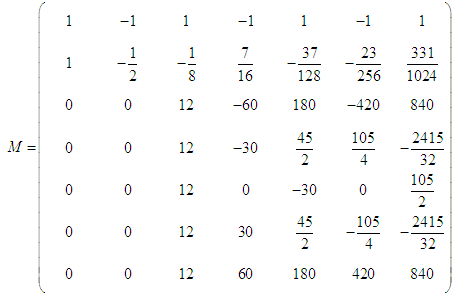
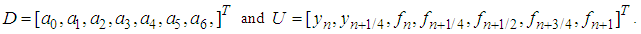 Solving (6) using Gaussian Elimination method in Maple soft environment produces the following values of
Solving (6) using Gaussian Elimination method in Maple soft environment produces the following values of 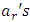 :
: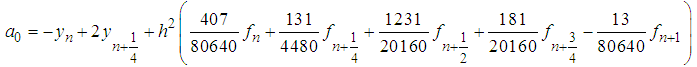 | (7) |
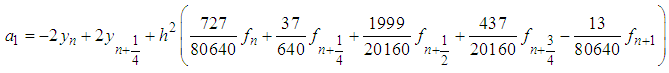 | (8) |
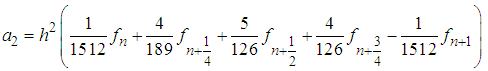 | (9) |
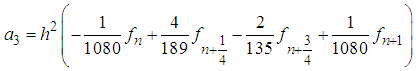 | (10) |
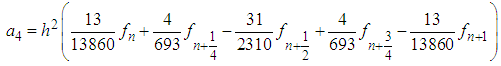 | (11) |
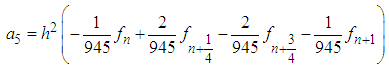 | (12) |
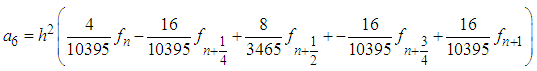 | (13) |
Substituting (7)-(13) into equation (3) and after some manipulation gives the continuous scheme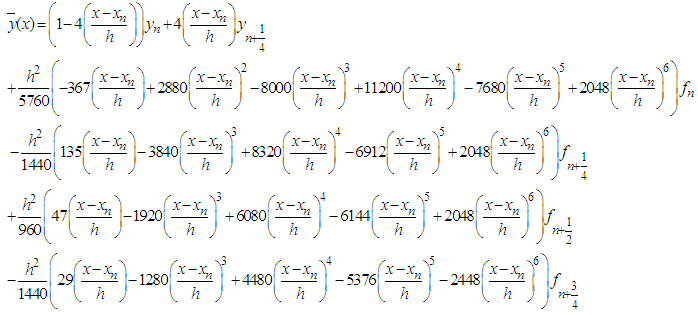 | (14) |
Evaluating (14) at 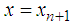 gives the discrete scheme
gives the discrete scheme 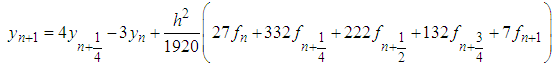 | (15) |
The discrete scheme (15) is consistent, zero-stable and of order 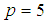 with error constant
with error constant 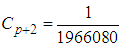 .Here, it is our intention to get additional discrete schemes, so, we evaluated (14) at the points
.Here, it is our intention to get additional discrete schemes, so, we evaluated (14) at the points 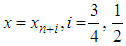 to obtain:
to obtain: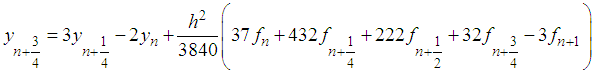 | (16) |
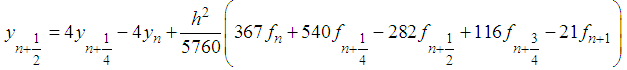 | (17) |
The first derivative of (14) is found and evaluated at points 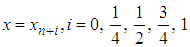 yields the following derivative schemes:
yields the following derivative schemes: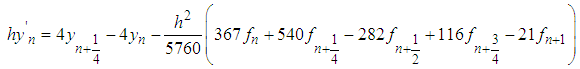 | (18) |
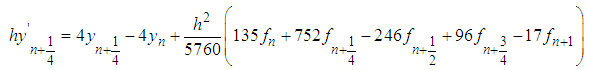 | (19) |
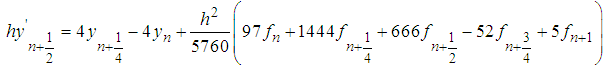 | (20) |
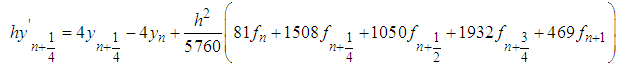 | (21) |
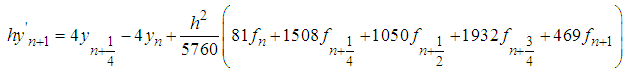 | (22) |
2.2. Implementation of the One-Step Continuous Hybrid Multistep Method (OSCHMM).
In this section, the implementation strategy of this work is discussed. Following Fatunla (1991, 1994), the general discrete block formula is given as: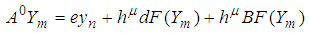 | (23) |
where e, d are vectors, B are RxR matrix and 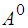 identity matrix, µ is the order of differential equation. Expressing equations (20) - (23) and (24) in form of (23) and solving with matrix inversion method gives:
identity matrix, µ is the order of differential equation. Expressing equations (20) - (23) and (24) in form of (23) and solving with matrix inversion method gives: 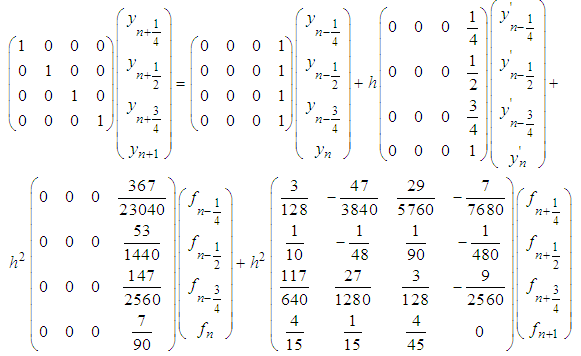 | (24) |
Writing (24) explicitly 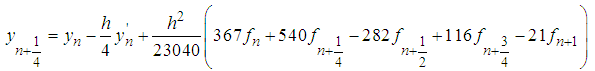 | (25) |
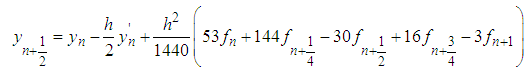 | (26) |
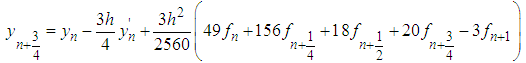 | (27) |
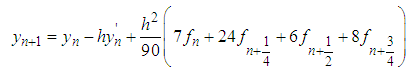 | (28) |
The block method is of uniform order 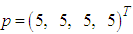 with error constant
with error constant 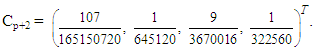 Substituting (25) into (19)-(22) yields
Substituting (25) into (19)-(22) yields 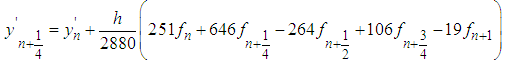 | (29) |
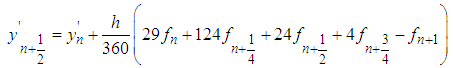 | (30) |
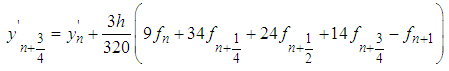 | (31) |
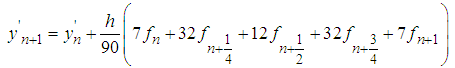 | (32) |
Equations (25)-(32) are then applied in block form as simultaneous numerical integrators to solve (1). CASE 2: Two-Step Continuous Hybrid Multistep Method (TSCHMM).Similarly, collocating (5) at points, and interpolating (3) at points 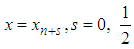 lead to a system of equations of form (6) where,
lead to a system of equations of form (6) where,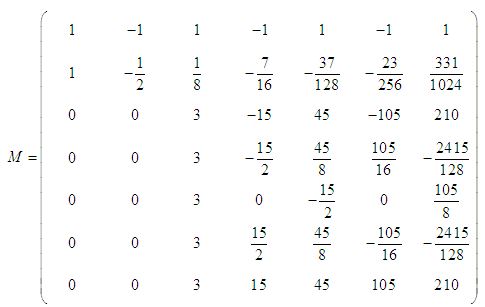
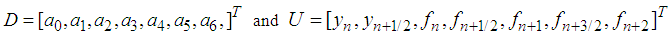 . The continuous scheme is as follows :
. The continuous scheme is as follows :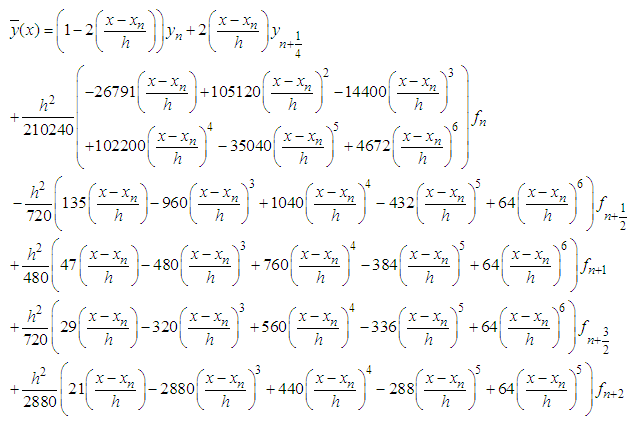 | (33) |
The discrete scheme is obtained as: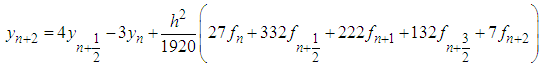 | (34) |
The discrete scheme (34) is consistent, zero-stable and of order 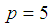 , with the error constant
, with the error constant 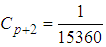 .Evaluating (33) at the points
.Evaluating (33) at the points 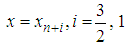 , we obtained the following discrete schemes:
, we obtained the following discrete schemes: 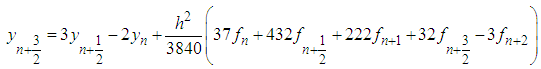 | (35) |
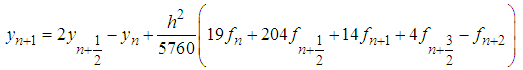 | (36) |
The first derivative of (33) is found and evaluated at points 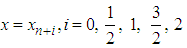 yield the following derivative schemes:
yield the following derivative schemes: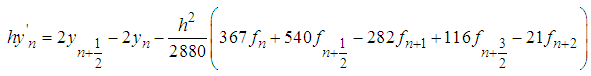 | (37) |
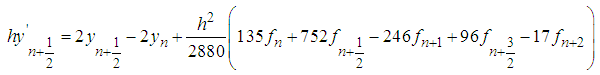 | (38) |
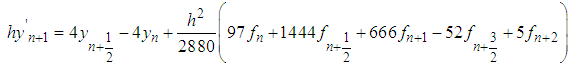 | (39) |
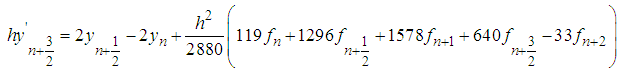 | (40) |
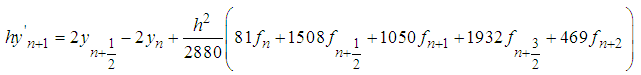 | (41) |
The implementation of Two-Step Continuous Hybrid Multistep Method (TSCHMM) is as follows:Combining (34), (35), (36), (37) and solving by using matrix inversion method gives: | (42) |
The above block method is of uniform order 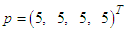 with the error constant
with the error constant 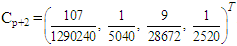 . Equations (38) -(41) with (42) are applied in block form as simultaneous numerical integrators to solve (1).
. Equations (38) -(41) with (42) are applied in block form as simultaneous numerical integrators to solve (1).
3. Stability Analysis
In the spirit of Sommeijer et al., (1992), the linear stability of block method can be investigated by applying the method to the test equation 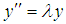 . This leads to a recursion of the form:
. This leads to a recursion of the form: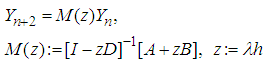 M is called the amplification matrix and its eigenvalues the amplification factors. By requiring the elements of the diagonal matrix D to be positive, the matrix
M is called the amplification matrix and its eigenvalues the amplification factors. By requiring the elements of the diagonal matrix D to be positive, the matrix 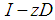 is nonsingular for all z on the negative real axis. Therefore, in the sequel, we assume that the (diagonal) elements of D are positive. We shall use the result on the power of a matrix N (Varga 1962),
is nonsingular for all z on the negative real axis. Therefore, in the sequel, we assume that the (diagonal) elements of D are positive. We shall use the result on the power of a matrix N (Varga 1962), 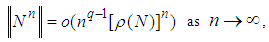 where and
where and 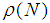 are the spectra norm and the radius of N and where all diagonal sub-matrices of the Jordan normal form of N which have spectral radius
are the spectra norm and the radius of N and where all diagonal sub-matrices of the Jordan normal form of N which have spectral radius 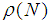 are at most qxq. If the spectra radius
are at most qxq. If the spectra radius 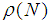 < 1, then N is called power bounded. The region where the amplification matrix M(z) is power bounded is called the stability region of the block method. If the stability region contains the origin, then the method is called the zero-stable. Below are the graphical representations of stability of OSCHMM and TSCHMM respectively.
< 1, then N is called power bounded. The region where the amplification matrix M(z) is power bounded is called the stability region of the block method. If the stability region contains the origin, then the method is called the zero-stable. Below are the graphical representations of stability of OSCHMM and TSCHMM respectively.
4. Numerical Experiments and Results
In this section, we applied the new methods to some problems: the first is Undamped Duffing’s equation of Fang and Wu (2008), two body problem of Fatunla (1990), stiff problem, linear second order initial value problem, Stiefel and Bettis problem and Implicit 3-point 1-block (I3P1B) of Fadzial (2009).Problem 1: The Undamped Duffing’s equation: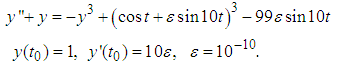 The exact solution
The exact solution 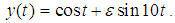 It describes a periodic motion of low frequency with a small perturbation of high frequency. The numerical results are shown on tables 1and 2 below.
It describes a periodic motion of low frequency with a small perturbation of high frequency. The numerical results are shown on tables 1and 2 below.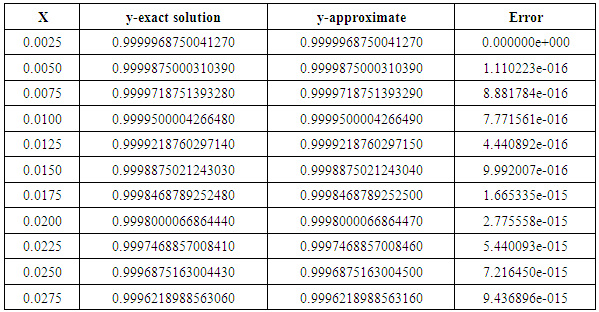 | Table 1. One-step method for problem 1 Undamped Duffing's Equation |
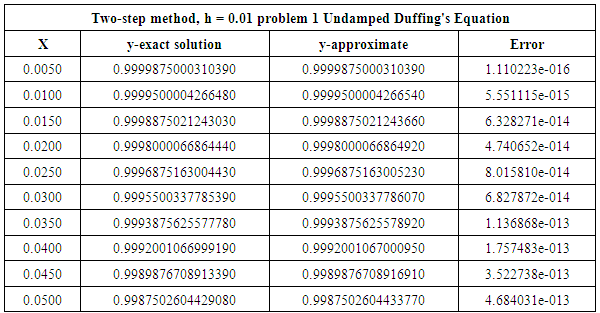 | Table 2. The y-exact, y-approximate and error of TSCHMM for problem 1 |
Problem 2: Consider the given two-body problem 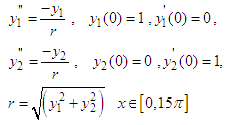 Theoretical solution:
Theoretical solution: 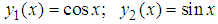 Problem 3: Consider the stiff problem
Problem 3: Consider the stiff problem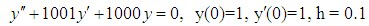 Theoretical solution:
Theoretical solution: 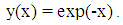 Problem 4:
Problem 4: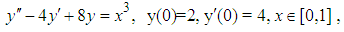 Theoretical solution:
Theoretical solution: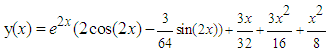 Problem 5: Consider the system of equations of Stiefel and Bettis problem:
Problem 5: Consider the system of equations of Stiefel and Bettis problem: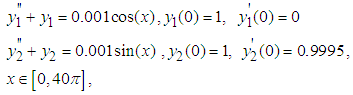 The exact solutions are given as:
The exact solutions are given as: 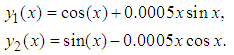 On tables 3 and 4, y-exact, y-computed and error of OSCHMM and TSCHMM for problem 2 are shown while the y-exact, y-computed and error of TSCHMM for problem 3 is shown on table 5. On table 6, it is observed that the maximum absolute error of the TSCHMM is 7.14260896951E-08 is (smaller) more accurate than 5.10704 E-06 of Jator & Li (2009) for problem 4.
On tables 3 and 4, y-exact, y-computed and error of OSCHMM and TSCHMM for problem 2 are shown while the y-exact, y-computed and error of TSCHMM for problem 3 is shown on table 5. On table 6, it is observed that the maximum absolute error of the TSCHMM is 7.14260896951E-08 is (smaller) more accurate than 5.10704 E-06 of Jator & Li (2009) for problem 4. 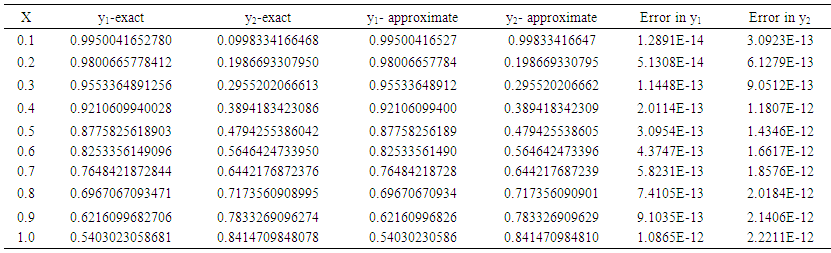 | Table 3. The y-exact, y-approximate and error of OSCHMM for problem 2Table 4: The y-exact, y-approximate and error of TSCHMM for problem 2 |
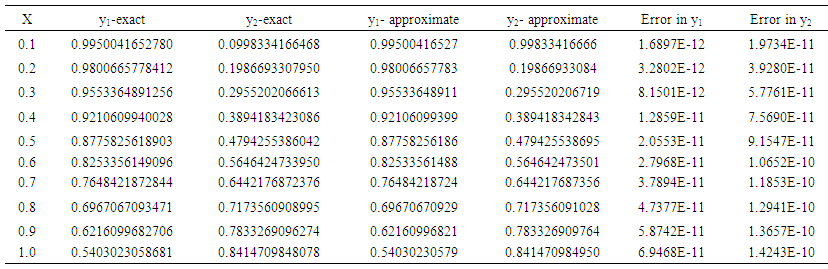 | Table 4. The y-exact, y-approximate and error of TSCHMM for problem 2 |
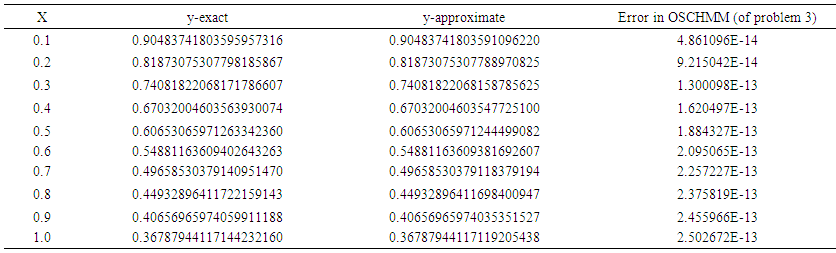 | Table 5. The y-exact, y-approximate and error of OSCHMM for problem 3 |
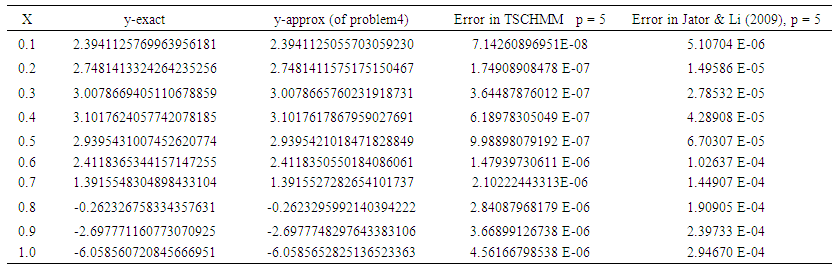 | Table 6. Accuracy Comparison of TSCHMM for Problem 4 |
The accuracy comparison of the new methods and I31PB are shown on table 7. The new One-step method (OSCHMM) and Two-step method (TSCHMM) are substantially more accurate than the numerical solution of initial-value problems (IVPs) using I3P1B, as the maximum absolute error is smaller with variable h is 9.115552(-10) while that the maximum absolute error of TSCHMM is 7.294766(-9) which is smaller than 2.14918(-8) of I3P1B for h = 0.01.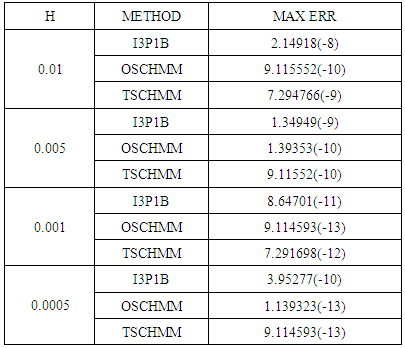 | Table 7. Accuracy Comparison of OSCHMM and TSCHMM with Implicit 3-point-1 block (13PIB) |
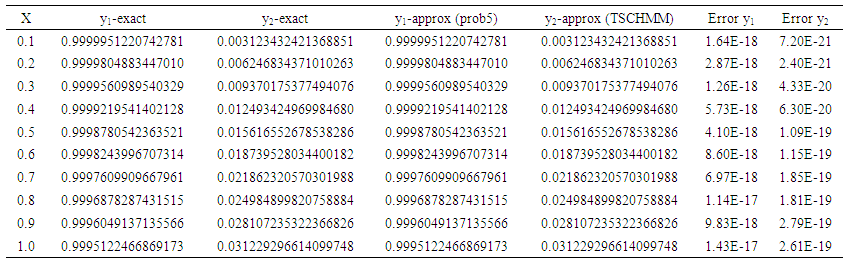 | Table 8. y-exact, y-approximate and error in TSCHMM for problem 5 |
5. Conclusions
We have presented continuous hybrid multistep methods with Legendre polynomial as basis function for the direct solution of system of second order ODEs. The derived methods were implemented in block mode which have the advantages of being self-starting, uniformly of the same order of accuracy and do not need predictors, having good accuracy as shown on table 7. It should be noted that accuracy and efficiency rate of a method is dependent on the implementation strategies. If economical computation is required, then the new methods are the better choice. The new methods are therefore recommended for general purposed use. Finally, the region of absolute stability of the block methods of One-step and Two-step methods were presented in figures 1 and 2. Maple and Matlab software package were employed to generate the schemes and results.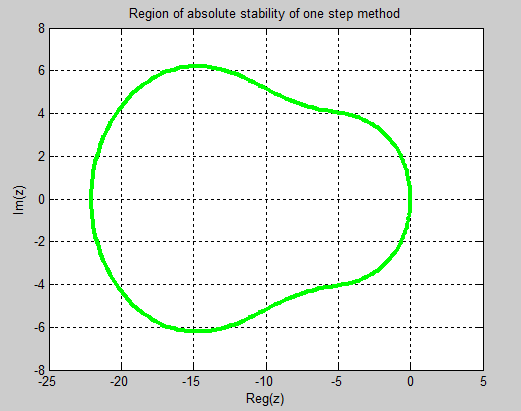 | Figure 1. Stability Domain of Block of OSCHMM which is A(α)-stable by Definition 1.3 |
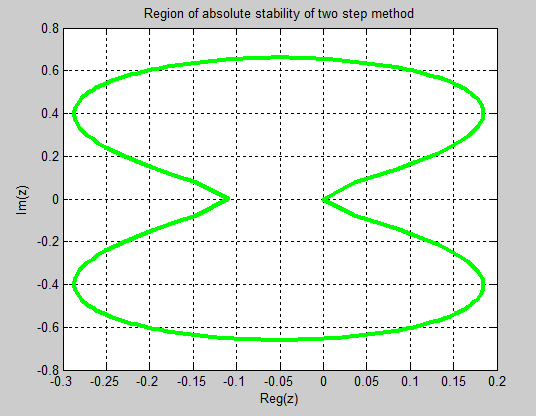 | Figure 2. Stability Domain of Block TSCHMM which is L(α)-stable by definition 1.3 and 1.4 |
References
| [1] | Abualnaja, K. M (2015) A Block Procedure with Linear Multistep Methods using Legendre Polynomial for Solving ODEs. Applied Mathematics SciRes, 6, pp717-723 http://dx.doi.org/10.4236/am.2015.64067. |
| [2] | Adeyefa, E. O. Folaranmi O. R. and A. F Adebisi, (2014), A Self-Starting First Order Initial Value Solver, In. J. Pure Appl. Sc. Technol., 25(1), 8-13. |
| [3] | Awari (2013) Derivation and Application of Six-Point Linear Multistep Numerical Method for the Solution of Second Order Initial Value Problems. IOSR Journal of Mathematics, e-ISSN: 2278-5728, p-ISSN 2319-765X, vol. 7, Issue 2, PP 23-29. |
| [4] | Awoyemi D. O and Idowu, O. M (2005) A Class of Hybrid Collocation Methods for Third Order Ordinary Differential Equations. International Journal of Computer Mathematics vol.82, No 00.pp1-7. |
| [5] | Ehigie, J.O (2010) On Generalized 2-Step Continuous Linear Multistep Method of Hybrid Type For The integration of Second Order Ordinary Differential Equations, Arch. Appl. Sci. Res., 2010,2(6):362-372. |
| [6] | Ehle, B. L. (1969): On Pade Approximations to the Exponential Junction and A-stable Methods for the Numerical Solution of Initial Value Problems. Research Report CSRR 2010, Dept. AACS, Univ. of Waterloo, Ontario, Canada. IV.5. |
| [7] | Fang, Y. L; Songa, Y and Wu, X. Y (2008) A Robust Trigonometrically Fitted Embedded Pair For Perturbed Oscillators. Journal of Computational and Applied Mathematics 225 (2009) 347-355. |
| [8] | Fatunla, S. O (1990) Block Method For Second Order ODEs. Inter. J. Compter Maths, 41(1990), pp55-63. |
| [9] | Fudzial, I ;Yap Lee Ken and Mohamad Othman (2009) Explicit and Implicit 3-Point Block Methods for Solving Special Second Order Ordinary Differential Equations Directly. Int. Journal of Math. Analysis, Vol. 3. No5, 239-254, pp239-253. |
| [10] | Hairer, E and Wanner, G (1996) Solving Ordinary Differential Equations II, Stiff and Differential –Algebraic Problems second revised edition ISBN3-540-60452-9 Springer-Verlag Berlin Heidelberg New York. pp 241. |
| [11] | Jator S. N and Li (2009) A Self-Starting Linear Multistep Method for the Direct Solution of General Second Order Initial Value Problem. International Journal of Computer Math. 86(5), 817-836. |
| [12] | Lambert, J. D. (1991) Numerical Solution for Ordinary Differential Systems, New York John Wiley, 1991. |
| [13] | Landau, L. D and Lifshitz, F. M. (1965) Quantum Mechanics, Pergamon, New York. |
| [14] | Liboff, R. L (1980) Introductory Quantum Mechanics, Addison-Wiley, Reading M. A 1980. |
| [15] | Olagunju, A.S; Joseph, F. L and Raji, M. T (2012) Comparative Study of The Effect of Different Collocation Point on Ledendre Collocation Methods of Solving Second Order Boundry Value Problems, IOSR Journal of Mathematics vol.7(2) pp 35-41. |
| [16] | Onumanyi, P; Oladele, J. O; Adeniyi, R. B and Awoyemi, D. O. (1993) Derivation of Finite Difference Methods by Collocation, Abacus, 23(2), 72-83. |
| [17] | Sirisena, U. W; Kumleng, G. M and Yahaya, Y.A (2004) A New Butcher Type Two-Step Block Hybrid Multistep Method For Accurate and Efficient Parallel Solution of ODEs. ABACUS Journal of Mathematical Association of Nigeria. Volume 31, Number 2A Mathematics series NR-ISSN0001-3099 pp1-7. |
| [18] | Sommeijer, B. P; Couzy, W. and Van De Houwen (1992) A-Stable Parallel Block Methods for Ordinary and Integro-Differential Equations, Applied Numerical Mathematics 9(1992) 267-281 North-Holland. |
| [19] | Yusuph Y and Onumanyi, P (2002) New Multiple FDMS Through Multistep Collocation for y″= f (x,y). Abacus vol. 29 No 2 Mathematics series. The Journal of Mathematical Association of Nigeria pp 92-100. |
| [20] | Varga, R. S (1962) Martix Iterative Analysis. Prentice-Hall, Englewood Cliffs, NJ, pp 65. |
| [21] | Widlund, O. B (1967): A note on unconditionally stable linear multistep methods. BIT, vol. 7, pp. 65-70. |



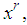 the canonical polynomial
the canonical polynomial 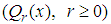 of the Lanczos Tau method in a perturbed collocation approach have been employed for this purpose (see Abualnaja (2015); Adeyefa et al., (2014); Awoyemi and Idowu (2005); Lambert (1991)).Moreover, power series has also being extensively used in literature for the same purpose. Sirisena et al., (2004) proposed a new Butcher type two-step block hybrid multistep method for accurate and efficient parallel solution of order ordinary differential equations. Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third order ordinary differential equations with power series as the basis functions and were implemented in predictor –corrector mode. Ehigie et al., (2010) worked on generalized two-step continuous linear multistep method of hybrid type for the direct integration of second order ordinary differential equations. Fudzial et al., (2009) constructed the explicit and implicit 3-point-1- block (I3P1B) for solving special second order ordinary equations directly. Awari (2013) considered the derivation and application of six-point linear multistep numerical method for the solution of second order initial value problems which was implemented in block mode. Yusuph and Onumanyi (2002) demonstrated a successful application of multiple finite difference methods through multistep collocation for the second order ordinary differential equations. Furthermore, Abualnaja (2015) constructed a block procedure with linear multistep methods using Legendre polynomial for solving first order ordinary differential equations. The method depends on the perturbed collocation approximation with Legendre as perturbation term for the solution of first order ordinary differential equations. In the work of Yakusak et al., (2015), uniform order Legendre approach for continuous hybrid block methods were proposed for the solution of first order ordinary differential equations. In this paper, we propose the choice of Legendre polynomial without perturbation as basis functions for the construction of continuous schemes, which simultaneously generate solution of (1). They are self-starting and do not need any predictors. PreliminariesA central notion in this work concerns the choice of Legendre polynomial as basis functions in the derivation of the continuous schemes, the implementation strategies employed (in block mode) and the stability analysis of the methods. For convenience of the reader, we recall the definitions as follows:Definition 1.1: The block method is said to be zero-stable if the roots
of the Lanczos Tau method in a perturbed collocation approach have been employed for this purpose (see Abualnaja (2015); Adeyefa et al., (2014); Awoyemi and Idowu (2005); Lambert (1991)).Moreover, power series has also being extensively used in literature for the same purpose. Sirisena et al., (2004) proposed a new Butcher type two-step block hybrid multistep method for accurate and efficient parallel solution of order ordinary differential equations. Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third order ordinary differential equations with power series as the basis functions and were implemented in predictor –corrector mode. Ehigie et al., (2010) worked on generalized two-step continuous linear multistep method of hybrid type for the direct integration of second order ordinary differential equations. Fudzial et al., (2009) constructed the explicit and implicit 3-point-1- block (I3P1B) for solving special second order ordinary equations directly. Awari (2013) considered the derivation and application of six-point linear multistep numerical method for the solution of second order initial value problems which was implemented in block mode. Yusuph and Onumanyi (2002) demonstrated a successful application of multiple finite difference methods through multistep collocation for the second order ordinary differential equations. Furthermore, Abualnaja (2015) constructed a block procedure with linear multistep methods using Legendre polynomial for solving first order ordinary differential equations. The method depends on the perturbed collocation approximation with Legendre as perturbation term for the solution of first order ordinary differential equations. In the work of Yakusak et al., (2015), uniform order Legendre approach for continuous hybrid block methods were proposed for the solution of first order ordinary differential equations. In this paper, we propose the choice of Legendre polynomial without perturbation as basis functions for the construction of continuous schemes, which simultaneously generate solution of (1). They are self-starting and do not need any predictors. PreliminariesA central notion in this work concerns the choice of Legendre polynomial as basis functions in the derivation of the continuous schemes, the implementation strategies employed (in block mode) and the stability analysis of the methods. For convenience of the reader, we recall the definitions as follows:Definition 1.1: The block method is said to be zero-stable if the roots 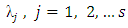 of the characteristic polynomial
of the characteristic polynomial 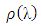 defined by
defined by 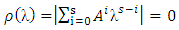 satisfies
satisfies 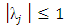 and for those roots with
and for those roots with 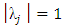 , the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals
, the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals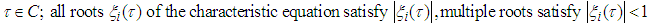 is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition: 1.3 (Widlund (1967))A method is said to be A(α)-stable if the sector
is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition: 1.3 (Widlund (1967))A method is said to be A(α)-stable if the sector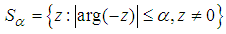 is contained in the stability region.Definition 1.4 (Ehle (1969)): A method is called L-stable if it is A-stable and if in addition
is contained in the stability region.Definition 1.4 (Ehle (1969)): A method is called L-stable if it is A-stable and if in addition 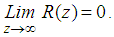 Definition 1.5 (Olagunju et al., (2012)): Legendre polynomial is special case of the Legendre function which satisfy the differential equation
Definition 1.5 (Olagunju et al., (2012)): Legendre polynomial is special case of the Legendre function which satisfy the differential equation 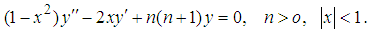 The general solution can be expressed as:
The general solution can be expressed as: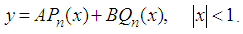
 and
and  are respectively the Legendre functions of the first-and second-kind of the order n. The nth order polynomial
are respectively the Legendre functions of the first-and second-kind of the order n. The nth order polynomial 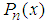 is generally given by the following equation:
is generally given by the following equation: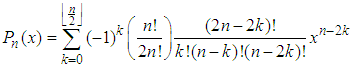 where n is the order of the Legendre polynomials,
where n is the order of the Legendre polynomials, 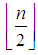 signifies the integer part of
signifies the integer part of 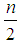 . Legendre polynomials are orthogonal to each other with respect to weight function w(x) = 1 on [-1,1]. The first two polynomials are always the same in all cases but the higher orders are created with recursive formula:
. Legendre polynomials are orthogonal to each other with respect to weight function w(x) = 1 on [-1,1]. The first two polynomials are always the same in all cases but the higher orders are created with recursive formula: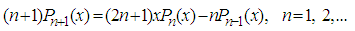 with initial conditions:
with initial conditions: 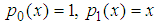 . The first four terms of the polynomial are;
. The first four terms of the polynomial are; 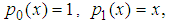
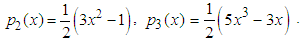 The paper is organized as follows. Section 1 is of an introductory nature. The materials and methods are described in Section 2. Stability analysis of the methods is discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.
The paper is organized as follows. Section 1 is of an introductory nature. The materials and methods are described in Section 2. Stability analysis of the methods is discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.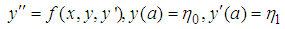
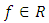 is sufficiently differentiable and satisfies a Lipschitz condition, sufficiently smooth,
is sufficiently differentiable and satisfies a Lipschitz condition, sufficiently smooth, 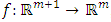 , y is an m-dimensional vector and
, y is an m-dimensional vector and 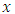 is a scalar variable and a set of equally spaced points on the integration interval also given by
is a scalar variable and a set of equally spaced points on the integration interval also given by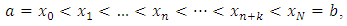
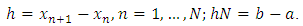 Assuming an approximate solution to (1) by taking the partial sum of Legendre polynomial of the form:
Assuming an approximate solution to (1) by taking the partial sum of Legendre polynomial of the form: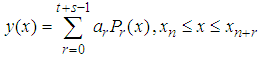
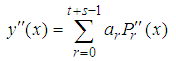
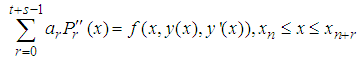
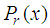 is the Legendre polynomial of degree
is the Legendre polynomial of degree 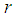 , valid in
, valid in 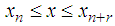 and
and 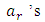 are real unknown parameters to be determined and
are real unknown parameters to be determined and 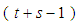 is the sum number of collocation and interpolation points. The well-known Legendre polynomials are defined on the interval [-1,1].
is the sum number of collocation and interpolation points. The well-known Legendre polynomials are defined on the interval [-1,1].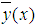 of degree
of degree 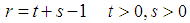 . Two cases were considered one-step and two-step methods.CASE 1: One-Step Continuous Hybrid Multistep Method (OSCHMM).Collocating (5) at points, and interpolating (3) at points
. Two cases were considered one-step and two-step methods.CASE 1: One-Step Continuous Hybrid Multistep Method (OSCHMM).Collocating (5) at points, and interpolating (3) at points 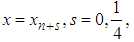 respectively lead to a system of equations expressed in matrix form:
respectively lead to a system of equations expressed in matrix form: 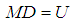
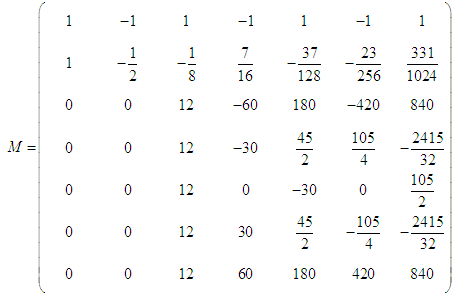
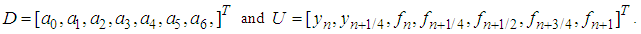 Solving (6) using Gaussian Elimination method in Maple soft environment produces the following values of
Solving (6) using Gaussian Elimination method in Maple soft environment produces the following values of 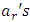 :
: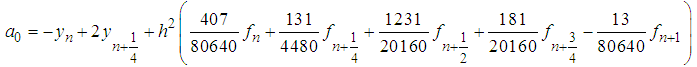
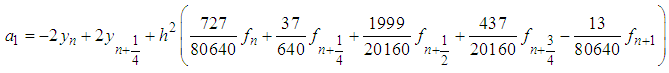
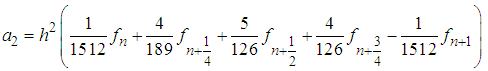
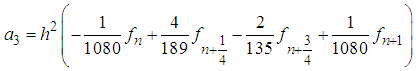
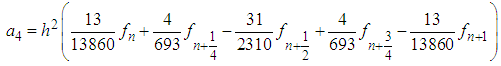
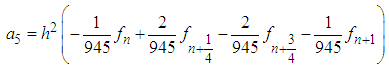
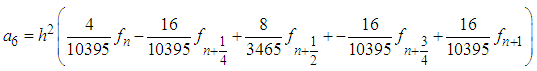
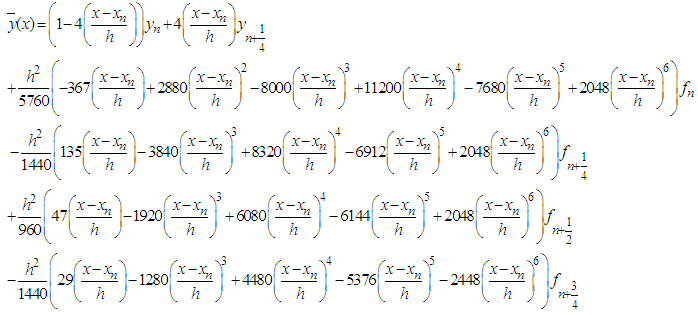
 gives the discrete scheme
gives the discrete scheme 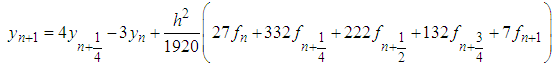
 with error constant
with error constant 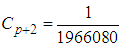 .Here, it is our intention to get additional discrete schemes, so, we evaluated (14) at the points
.Here, it is our intention to get additional discrete schemes, so, we evaluated (14) at the points 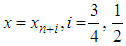 to obtain:
to obtain: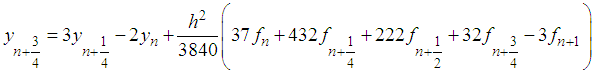
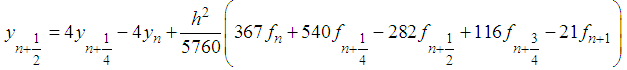
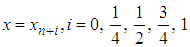 yields the following derivative schemes:
yields the following derivative schemes: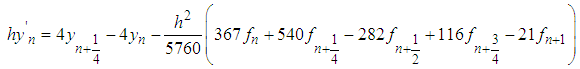
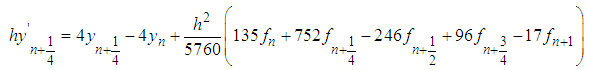
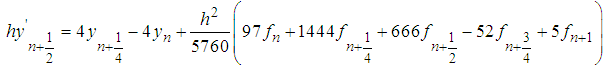
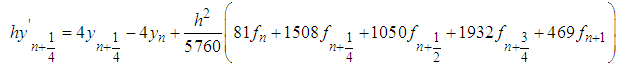
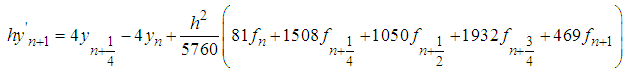
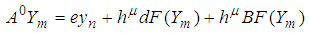
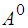 identity matrix, µ is the order of differential equation. Expressing equations (20) - (23) and (24) in form of (23) and solving with matrix inversion method gives:
identity matrix, µ is the order of differential equation. Expressing equations (20) - (23) and (24) in form of (23) and solving with matrix inversion method gives: 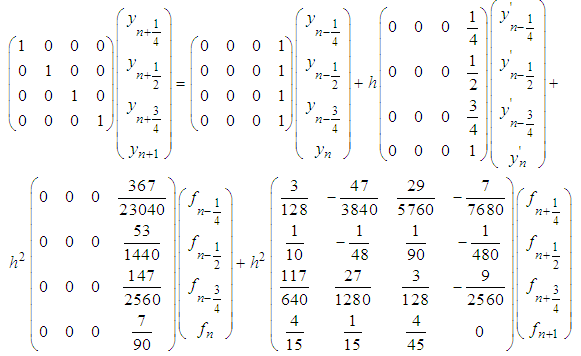
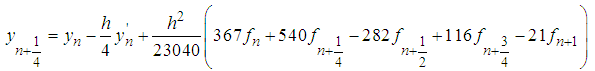
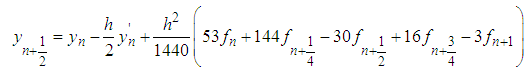
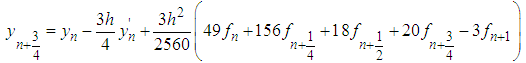
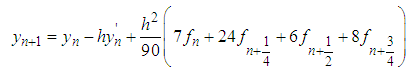
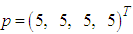 with error constant
with error constant 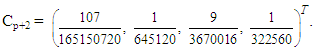 Substituting (25) into (19)-(22) yields
Substituting (25) into (19)-(22) yields 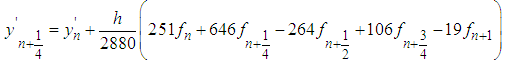
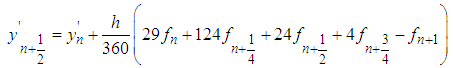
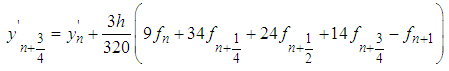
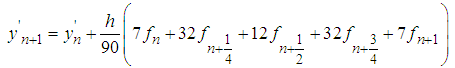
 lead to a system of equations of form (6) where,
lead to a system of equations of form (6) where,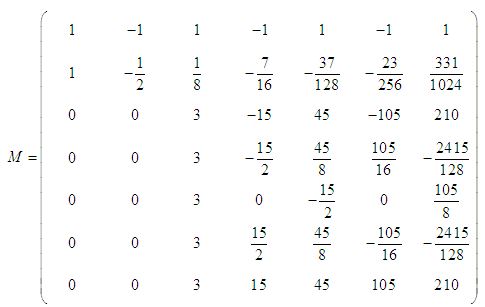
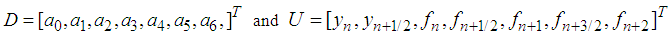 . The continuous scheme is as follows :
. The continuous scheme is as follows :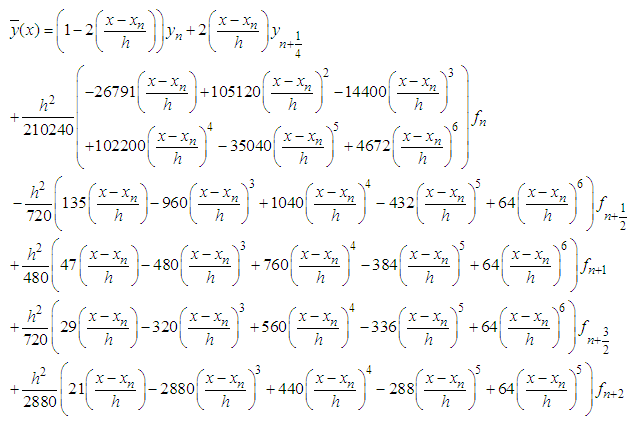
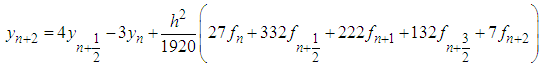
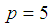 , with the error constant
, with the error constant 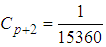 .Evaluating (33) at the points
.Evaluating (33) at the points 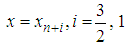 , we obtained the following discrete schemes:
, we obtained the following discrete schemes: 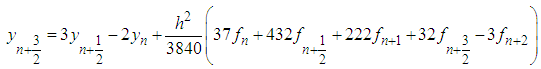
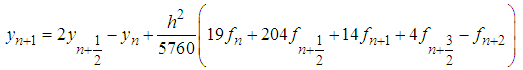
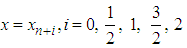 yield the following derivative schemes:
yield the following derivative schemes: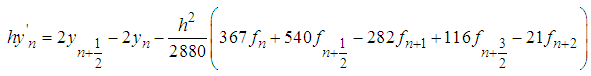
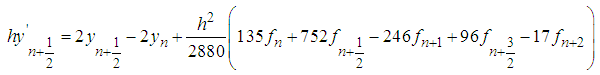
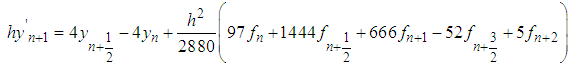
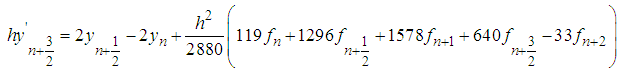
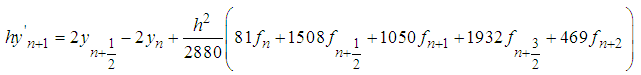

 with the error constant
with the error constant 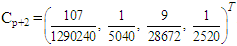 . Equations (38) -(41) with (42) are applied in block form as simultaneous numerical integrators to solve (1).
. Equations (38) -(41) with (42) are applied in block form as simultaneous numerical integrators to solve (1).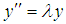 . This leads to a recursion of the form:
. This leads to a recursion of the form: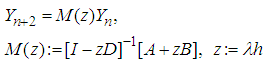 M is called the amplification matrix and its eigenvalues the amplification factors. By requiring the elements of the diagonal matrix D to be positive, the matrix
M is called the amplification matrix and its eigenvalues the amplification factors. By requiring the elements of the diagonal matrix D to be positive, the matrix 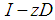 is nonsingular for all z on the negative real axis. Therefore, in the sequel, we assume that the (diagonal) elements of D are positive. We shall use the result on the power of a matrix N (Varga 1962),
is nonsingular for all z on the negative real axis. Therefore, in the sequel, we assume that the (diagonal) elements of D are positive. We shall use the result on the power of a matrix N (Varga 1962), 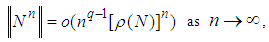 where and
where and 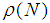 are the spectra norm and the radius of N and where all diagonal sub-matrices of the Jordan normal form of N which have spectral radius
are the spectra norm and the radius of N and where all diagonal sub-matrices of the Jordan normal form of N which have spectral radius 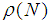 are at most qxq. If the spectra radius
are at most qxq. If the spectra radius 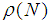 < 1, then N is called power bounded. The region where the amplification matrix M(z) is power bounded is called the stability region of the block method. If the stability region contains the origin, then the method is called the zero-stable. Below are the graphical representations of stability of OSCHMM and TSCHMM respectively.
< 1, then N is called power bounded. The region where the amplification matrix M(z) is power bounded is called the stability region of the block method. If the stability region contains the origin, then the method is called the zero-stable. Below are the graphical representations of stability of OSCHMM and TSCHMM respectively.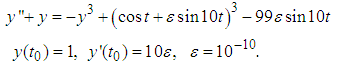 The exact solution
The exact solution 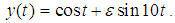 It describes a periodic motion of low frequency with a small perturbation of high frequency. The numerical results are shown on tables 1and 2 below.
It describes a periodic motion of low frequency with a small perturbation of high frequency. The numerical results are shown on tables 1and 2 below.

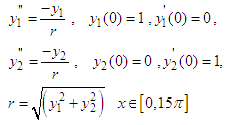 Theoretical solution:
Theoretical solution: 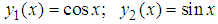 Problem 3: Consider the stiff problem
Problem 3: Consider the stiff problem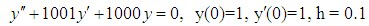 Theoretical solution:
Theoretical solution: 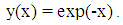 Problem 4:
Problem 4: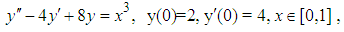 Theoretical solution:
Theoretical solution: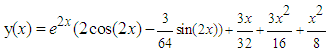 Problem 5: Consider the system of equations of Stiefel and Bettis problem:
Problem 5: Consider the system of equations of Stiefel and Bettis problem: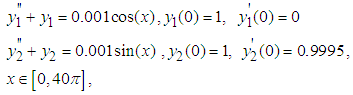 The exact solutions are given as:
The exact solutions are given as: 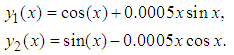 On tables 3 and 4, y-exact, y-computed and error of OSCHMM and TSCHMM for problem 2 are shown while the y-exact, y-computed and error of TSCHMM for problem 3 is shown on table 5. On table 6, it is observed that the maximum absolute error of the TSCHMM is 7.14260896951E-08 is (smaller) more accurate than 5.10704 E-06 of Jator & Li (2009) for problem 4.
On tables 3 and 4, y-exact, y-computed and error of OSCHMM and TSCHMM for problem 2 are shown while the y-exact, y-computed and error of TSCHMM for problem 3 is shown on table 5. On table 6, it is observed that the maximum absolute error of the TSCHMM is 7.14260896951E-08 is (smaller) more accurate than 5.10704 E-06 of Jator & Li (2009) for problem 4. 







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML