-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2016; 6(1): 1-6
doi:10.5923/j.ajcam.20160601.01

On a Certain Subclass of Harmonic Multivalent Functions
Waggas Galib Atshan 1, Enaam Hadi Abd 2, 3
1Department of Mathematics, College of Computer Science and Mathematics, University of Al-Qadisiya, Diwaniya, Iraq
2Department of Computer, College of Science, University of Kerbala, Kerbala, Iraq
3Department of Mathematics, College of Science, University of Baghdad, Baghdad, Iraq
Correspondence to: Waggas Galib Atshan , Department of Mathematics, College of Computer Science and Mathematics, University of Al-Qadisiya, Diwaniya, Iraq.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, we introduce a certain subclass of harmonic multivalent functions in the unit disk 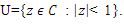 We obtain some interesting properties, like, coefficient conditions, convex set, distortion theorems, weighted mean.
We obtain some interesting properties, like, coefficient conditions, convex set, distortion theorems, weighted mean.
Keywords: Harmonic multivalent functions, Distortion theorem, Convex set
Cite this paper: Waggas Galib Atshan , Enaam Hadi Abd , On a Certain Subclass of Harmonic Multivalent Functions, American Journal of Computational and Applied Mathematics , Vol. 6 No. 1, 2016, pp. 1-6. doi: 10.5923/j.ajcam.20160601.01.
Article Outline
1. Introduction
- A continuous function
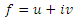 is a complex-valued harmonic function in a domain
is a complex-valued harmonic function in a domain 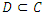 if both u and v are real harmonic in D. In any simply connected domain
if both u and v are real harmonic in D. In any simply connected domain 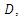 we can write
we can write 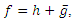 where h and g are analytic in D. We call h the analytic part and g the co-analytic part of f. The harmonic function
where h and g are analytic in D. We call h the analytic part and g the co-analytic part of f. The harmonic function 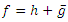 is sense-preserving and locally one-to-one in D if
is sense-preserving and locally one-to-one in D if  in D. See Clunie and Sheil-Small [3].For
in D. See Clunie and Sheil-Small [3].For  denote by
denote by  the class of functions
the class of functions 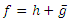 that are harmonic multivalent and sense-preserving in the unit disk
that are harmonic multivalent and sense-preserving in the unit disk 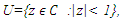 where
where 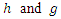 are defined by
are defined by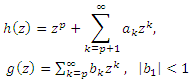 | (1) |
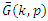 subclass of
subclass of 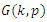 consisting of harmonic functions
consisting of harmonic functions 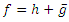 where
where 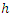 and
and 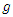 are of the form
are of the form 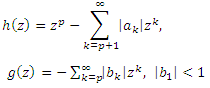 | (2) |
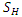 and as well as its geometric subclasses and obtained some coefficient bounds. Since then, there have been several related papers on
and as well as its geometric subclasses and obtained some coefficient bounds. Since then, there have been several related papers on  and its subclasses. For more basic results one may refer to the following standard introductory text book by Duren [4], see also Ahuja [1], Jahangiri et al. [5] and Ponnusamy and Rasila ([6], [7]).The convolution of two functions of form
and its subclasses. For more basic results one may refer to the following standard introductory text book by Duren [4], see also Ahuja [1], Jahangiri et al. [5] and Ponnusamy and Rasila ([6], [7]).The convolution of two functions of form 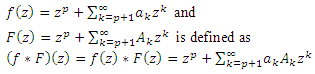 | (3) |
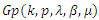 denote the subclass of
denote the subclass of 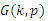 consisting of functions
consisting of functions 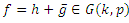 that satisfy the condition
that satisfy the condition 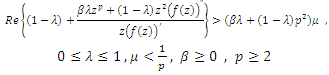 | (4) |
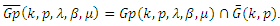 Lemma (1) [2]: Let
Lemma (1) [2]: Let 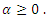 Then
Then 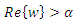 if and only if
if and only if 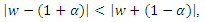 where w be any complex number.
where w be any complex number.2. Coefficient Estimates
- We begin with a sufficient condition for the function in
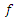 to be the class
to be the class 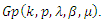 Theorem (2.1): Let
Theorem (2.1): Let 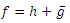 defined in (1). If
defined in (1). If 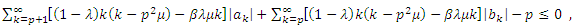 | (5) |
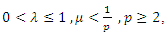 then
then 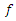 is harmonic Multivalent sense-preserving in U and
is harmonic Multivalent sense-preserving in U and 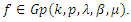 Proof: Let
Proof: Let 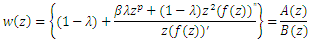 By lemma (1), we must show that (4) holds true. It suffices to show that
By lemma (1), we must show that (4) holds true. It suffices to show that 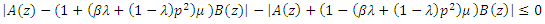 Substituting for w and resorting to simple calculation, we find
Substituting for w and resorting to simple calculation, we find Theorem (2.2): Let
Theorem (2.2): Let 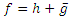 with h and g given by (2). Then
with h and g given by (2). Then 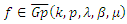 if and only if
if and only if 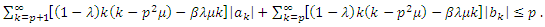 | (6) |
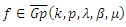 using (4), we get
using (4), we get 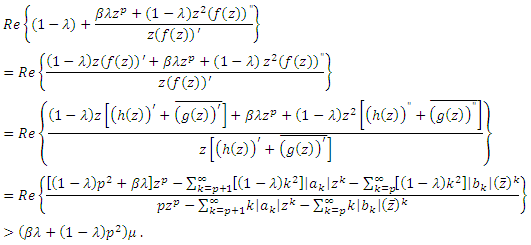 If we choose z to be real and let
If we choose z to be real and let 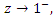 we obtain the condition (6) and the proof is complete.
we obtain the condition (6) and the proof is complete.3. Convex Set
- Theorem (3.1): The class
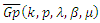 is convex set.Proof: Let the function
is convex set.Proof: Let the function 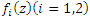 be in the class
be in the class 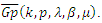 It is sufficient to show that the function
It is sufficient to show that the function  defined by:
defined by: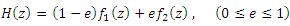 | (7) |
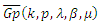 we have
we have 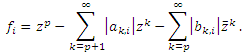 Since for
Since for 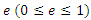
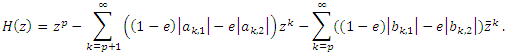 In view of Theorem (2.1), we have
In view of Theorem (2.1), we have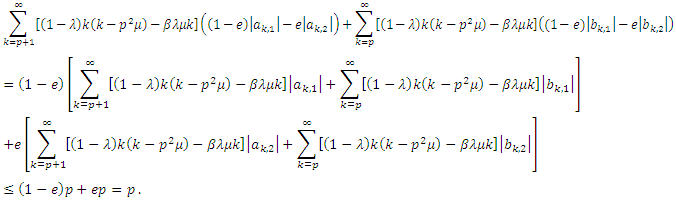 Hence,
Hence, 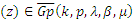 . This completes the proof.
. This completes the proof.4. Distortion and Covering
- The next Theorem is on the distortion and covering bounds for functions in the class
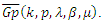 Theorem (4.1): If
Theorem (4.1): If 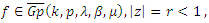 then
then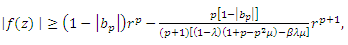 | (8) |
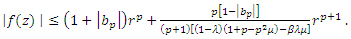 | (9) |
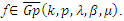 Then by Theorem (2.2), we obtain
Then by Theorem (2.2), we obtain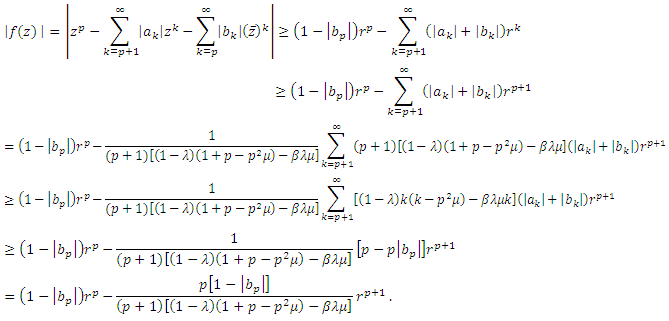 Relation (9) can be proved by using the similar statements. The covering result given in corollary (4.2) follows from the inequality (9) of this Theorem.Corollary(4.2): If
Relation (9) can be proved by using the similar statements. The covering result given in corollary (4.2) follows from the inequality (9) of this Theorem.Corollary(4.2): If 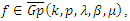 then
then 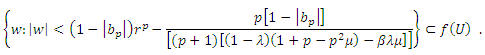
5. Weighted Mean
- Definition (5.1): Let
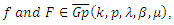 where
where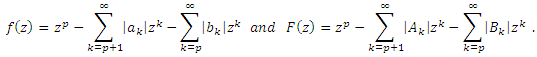 Then the weighted mean
Then the weighted mean 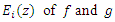 is given by
is given by 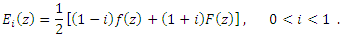 In the theorem below, we will show the weighted mean for this class:Theorem (5.2): If
In the theorem below, we will show the weighted mean for this class:Theorem (5.2): If 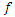 and
and 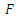 be in the class
be in the class 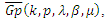 then the weighted mean of
then the weighted mean of 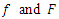 is also in the class
is also in the class 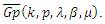 Proof: By Definition (5.1), we have
Proof: By Definition (5.1), we have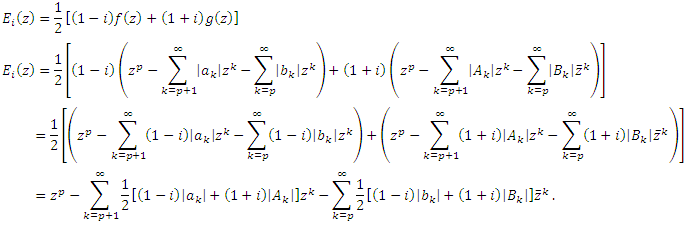 Since
Since 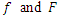 are in the class
are in the class 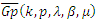 so by Theorem (2.2), we get
so by Theorem (2.2), we get 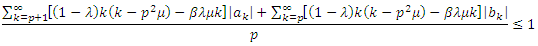 and
and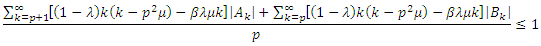 Then
Then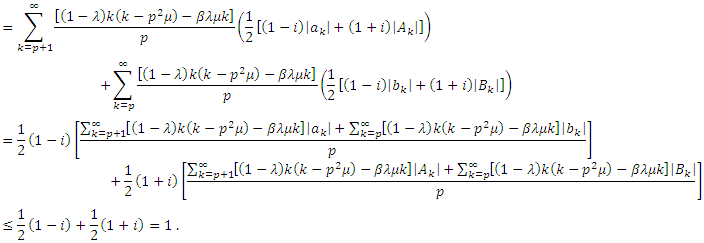
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML