-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2015; 5(6): 182-188
doi:10.5923/j.ajcam.20150506.05

Nth Order Pulse Solitary Wave Solution and Modulational Instability in the Boussinesq Equation
Jean Roger Bogning
Department of Physics, Higher Teacher Training College, University of Bamenda, Bamenda, Cameroon
Correspondence to: Jean Roger Bogning, Department of Physics, Higher Teacher Training College, University of Bamenda, Bamenda, Cameroon.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We look for the nth order exact pulse solitary wave solutions of the Boussinesq equation. For this reason, we define and find out all the solutions of the generalized Boussinesq equation. We later on deduce the solutions of classical Boussinesq equation. The modulational instability of the pulse solitary wave solutions obtained is also investigated in detail by using the Bogning- Djeumen Tchaho- Kofané method.
Keywords: Generalized Boussinesq equation, Solitary waves, Modulational Instability
Cite this paper: Jean Roger Bogning, Nth Order Pulse Solitary Wave Solution and Modulational Instability in the Boussinesq Equation, American Journal of Computational and Applied Mathematics , Vol. 5 No. 6, 2015, pp. 182-188. doi: 10.5923/j.ajcam.20150506.05.
Article Outline
1. Introduction
- The French physicist Joseph Boussinesq appears among many precursors of the nonlinear physics to the 19th century. His talent allowed him to do many works in the domain of the soil mechanics and especially of the fluid mechanics. He succeeded in modeled a nonlinear partial differential equation that describes the dynamics of propagation of the waves in little deep waters. This equation that carries his name is an equation that is going to revolutionize the domain of the hydrodynamics [1-7]. So, Apart from Korteweg – de Vries (KdV) equation, one of the equations that better describes the dynamics of shallow water waves in the oceanography context is the Boussinesq equation. If the KdV equation is definitely well known through its solitary wave solution, the Boussinesq equation continues to reveal the supplementary information according to approximations, it can be suggested. As all other nonlinear partial differential equation, there exist various methods of analysis the Boussinesq equation. Some of the commonly used techniques are the variational iteration method, the semi- inverse variational principle, the
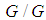 - expansion method, the exp-function method, the F-expansion methods and many others [8-15]. Beyond several methods that can contribute to solving the nonlinear partial differential equations of this order, many authors made different analyses on the Boussinesq equations [16-18]. Our work in this article is to determine the nth order solitary wave solutions of the form
- expansion method, the exp-function method, the F-expansion methods and many others [8-15]. Beyond several methods that can contribute to solving the nonlinear partial differential equations of this order, many authors made different analyses on the Boussinesq equations [16-18]. Our work in this article is to determine the nth order solitary wave solutions of the form 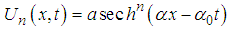 of the Boussinesq equation with cubic non linearity and establish their modulational instability criteria with the help of Bogning – Djeumen Tchaho – Kofané method (BDkm) [18-23]. Thus, this work is organized as follow: In section two, we define the generalized Boussinesq equation and obtain the range equations of coefficients. Section three analyses and proposes different solutions of the generalized and classical Boussinesq equation. In section four we study the modulational instability of the obtained solitary wave solution in the generalized Boussinesq equation and in the classical Boussinesq equation. Finally, we end the work by a general conclusion.
of the Boussinesq equation with cubic non linearity and establish their modulational instability criteria with the help of Bogning – Djeumen Tchaho – Kofané method (BDkm) [18-23]. Thus, this work is organized as follow: In section two, we define the generalized Boussinesq equation and obtain the range equations of coefficients. Section three analyses and proposes different solutions of the generalized and classical Boussinesq equation. In section four we study the modulational instability of the obtained solitary wave solution in the generalized Boussinesq equation and in the classical Boussinesq equation. Finally, we end the work by a general conclusion.2. Method and Range Equations Deriving from the Boussinesq Equation
- Boussinesq equation in its classical form is given by
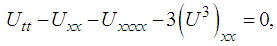 | (1) |
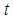 and the subscript
and the subscript 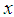 stand respectively for the derivative with respect to time and space. But in our analysis, we are going to consider Boussinesq equation under its generalized form
stand respectively for the derivative with respect to time and space. But in our analysis, we are going to consider Boussinesq equation under its generalized form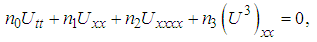 | (2) |
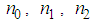 and
and  are the real numbers to be determined. Thus, looking for the solution of equation (2) in the form
are the real numbers to be determined. Thus, looking for the solution of equation (2) in the form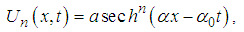 | (3) |
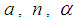 and
and 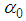 are real to be determined, we obtain via the transformations of reference [19, 20, 24], the following equation
are real to be determined, we obtain via the transformations of reference [19, 20, 24], the following equation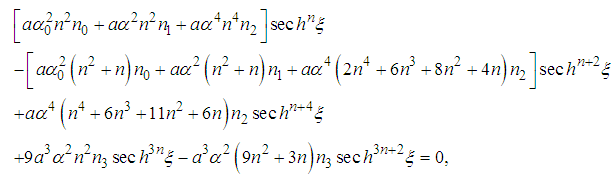 | (4) |
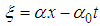 . Equation (4) is called general range equations of coefficients for any n. This equation is the main equation which will determined all the possibilities to obtain the solutions of equation (2).
. Equation (4) is called general range equations of coefficients for any n. This equation is the main equation which will determined all the possibilities to obtain the solutions of equation (2).3. Analysis of Equation (4) and Results
- Equation (4) obtained to the following analysis: we check the values of
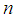 for which the terms in
for which the terms in 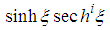 with
with 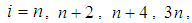 and
and 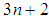 are identical. The terms in
are identical. The terms in 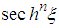 and
and 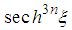 are identical for
are identical for 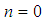 , the terms in
, the terms in 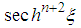 and
and 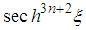 for
for 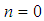 ; the terms in
; the terms in 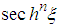 and
and 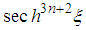 are identical for
are identical for 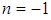 ; the terms in
; the terms in 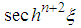 and
and 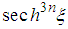 are identical for
are identical for 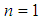 , the terms in
, the terms in 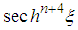 and
and 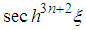 are identical for
are identical for 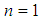 ; the terms in
; the terms in 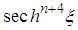 and
and 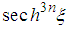 are identical for . These values are obtained just by equalizing different values of
are identical for . These values are obtained just by equalizing different values of 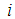 (for example
(for example 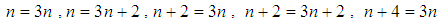 and
and 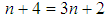 ). So for
). So for 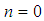 ,
, 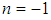 and , equation(4) admits only the trivial solutions. The acceptable solutions of equation (4) are obtained only for
and , equation(4) admits only the trivial solutions. The acceptable solutions of equation (4) are obtained only for 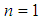 , equation (4) becomes.
, equation (4) becomes. 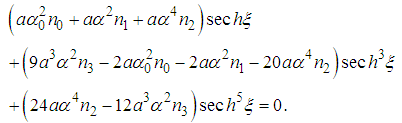 | (5) |
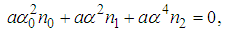 | (6) |
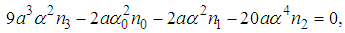 | (7) |
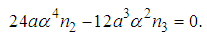 | (8) |
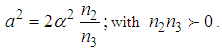 | (9) |
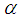 . Taking into account the fact that the equation (2) must be of the Boussinesq form such that
. Taking into account the fact that the equation (2) must be of the Boussinesq form such that 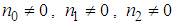 and
and 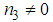 with
with 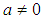 , the discriminant is
, the discriminant is 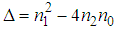 ; According to the values of
; According to the values of  , we look for the different solutions of equation (6).- For
, we look for the different solutions of equation (6).- For 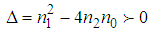 , we obtain
, we obtain 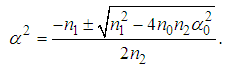 | (10) |
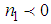 ,
, 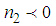 and
and 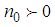
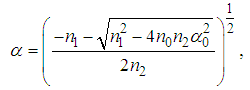 | (11) |
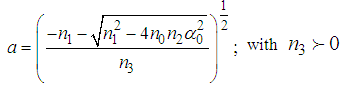 | (12) |
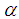 and
and 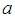 by their respective expression given by equations (11) and (12) in the ansatz (3), we obtain
by their respective expression given by equations (11) and (12) in the ansatz (3), we obtain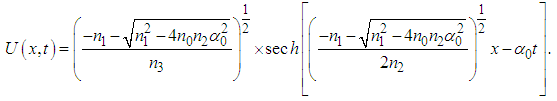 | (13) |
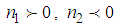 and
and 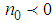 , from equation (10), we deduce the expression of
, from equation (10), we deduce the expression of 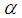 as
as 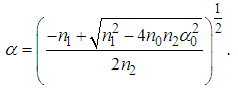 | (14) |
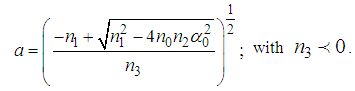 | (15) |
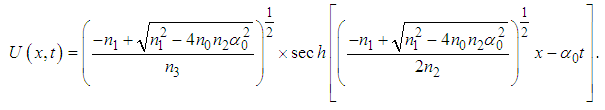 | (16) |
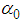 must be chosen such that these solutions are possible.- For
must be chosen such that these solutions are possible.- For 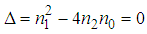 , we obtain
, we obtain 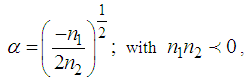 | (17) |
 | (18) |
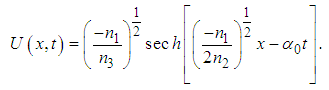 | (19) |
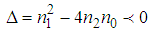 , we obtain from equation (6)
, we obtain from equation (6)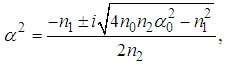 | (20) |
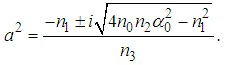 | (21) |
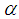 and
and 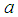 are complexes and we can also deduce the series of solutions linked.From the above analyses, we deduce the analytical solution of the classical Boussinesq equation (1) by setting
are complexes and we can also deduce the series of solutions linked.From the above analyses, we deduce the analytical solution of the classical Boussinesq equation (1) by setting 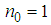 ,
, 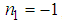 ,
, 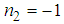 and
and 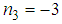 . Thus, from equation (13) we obtain
. Thus, from equation (13) we obtain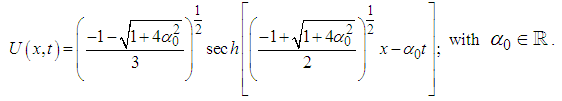 | (22) |
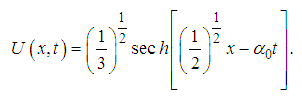 | (23) |
4. Modulational Instability of Bright Solitary Wave in Boussinesq Equation
- We analyse the modulational instability of the generalized Boussinesq equation (2), by looking for its solution in the form
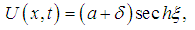 | (24) |
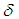 is the smallest term of perturbation which varies as a function of time and space. The solution here is chosen in the form given by equation (24) because we have verified in the preceeding section that the generalized Boussinesq equation admits the
is the smallest term of perturbation which varies as a function of time and space. The solution here is chosen in the form given by equation (24) because we have verified in the preceeding section that the generalized Boussinesq equation admits the 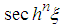 -solution only in the case where
-solution only in the case where 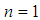 . Thus, inserting equation (24) in equation (2), we obtain
. Thus, inserting equation (24) in equation (2), we obtain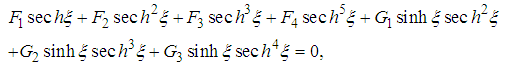 | (25) |
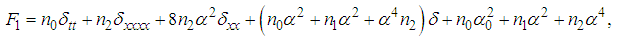 | (26) |
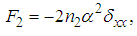 | (27) |
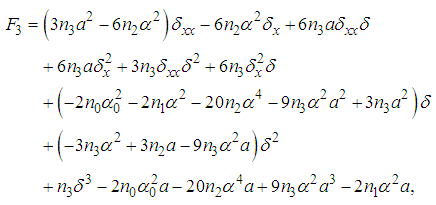 | (28) |
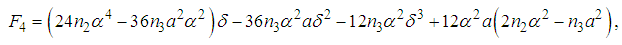 | (29) |
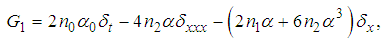 | (30) |
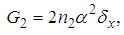 | (31) |
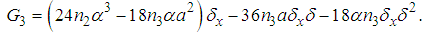 | (32) |
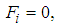 for
for 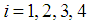 and
and 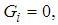 for
for 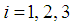 . According to the analysis made in references [19, 20, 24], the equation which is susceptible to express better the perturbation is given by the term in
. According to the analysis made in references [19, 20, 24], the equation which is susceptible to express better the perturbation is given by the term in 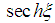 , but we also take into account that
, but we also take into account that 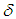 is a very small parameter. So the term in
is a very small parameter. So the term in 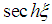 leads to
leads to 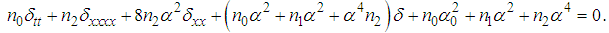 | (33) |
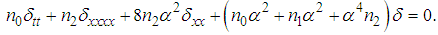 | (34) |
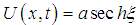 . If we suppose that the term of perturbation is given by
. If we suppose that the term of perturbation is given by 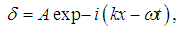 | (35) |
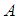 is an arbitrary constant, equation (34) leads to
is an arbitrary constant, equation (34) leads to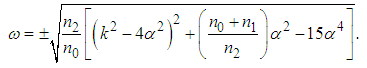 | (36) |
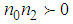 and
and 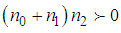 , the dispersion relation (36) is valid for
, the dispersion relation (36) is valid for 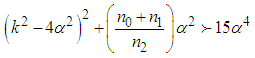 such that for
such that for 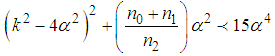 the dispersion relation is not valid and the modulational instability occurs. In this condition, equation (36) is written
the dispersion relation is not valid and the modulational instability occurs. In this condition, equation (36) is written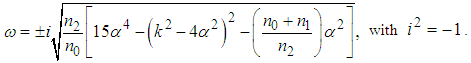 | (37) |
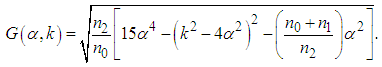 | (38) |
 and
and 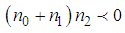 , the dispersion relation (36) is valid for
, the dispersion relation (36) is valid for 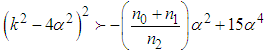 such that for
such that for 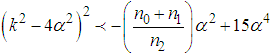 the dispersion relation is not valid and the modulational instability occurs. In this condition, equation (36) is written
the dispersion relation is not valid and the modulational instability occurs. In this condition, equation (36) is written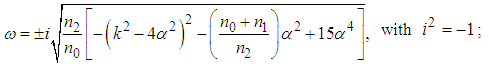 | (39) |
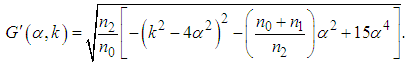 | (40) |
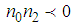 , equation (36) becomes equation (39) and vice versa.
, equation (36) becomes equation (39) and vice versa. 5. Conclusions
- Our aim was to construct solutions of shape
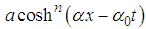 of Boussinesq equation and to study the modulational instability of these solutions By the Bogning – Djeumen Tchaho Kofané method. To attain our objective, we define the generalized Boussinesq equation by changing the knowing coefficients by the unknown coefficients such that the equation can be written
of Boussinesq equation and to study the modulational instability of these solutions By the Bogning – Djeumen Tchaho Kofané method. To attain our objective, we define the generalized Boussinesq equation by changing the knowing coefficients by the unknown coefficients such that the equation can be written 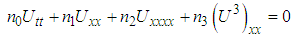 . This equation will call the generalized Boussinesq equation. So looking for the general solution of the generalized Boussinesq equation as indicated previously, we see that this type of solution exists only for and according to the values of coefficients
. This equation will call the generalized Boussinesq equation. So looking for the general solution of the generalized Boussinesq equation as indicated previously, we see that this type of solution exists only for and according to the values of coefficients 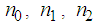 and
and 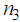 . After the general resolution of the generalized Boussinesq equation, we deduce from the resulting solutions the solution of the classical Boussinesq equation by setting
. After the general resolution of the generalized Boussinesq equation, we deduce from the resulting solutions the solution of the classical Boussinesq equation by setting 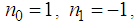
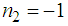 and
and 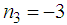 . The report we make is that we can obtain many modified Boussinesq equations which admit the solution of the type
. The report we make is that we can obtain many modified Boussinesq equations which admit the solution of the type 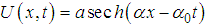 by choosing adequately the values of
by choosing adequately the values of 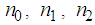 and
and 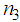 . We also investigate the modulational instability of such solitary wave solution in the generalized Boussinesq equation. We found out the general condition for which this modulational instability is possible. Finally, we deduce from the general criteria the criteria of modulational instability in the classical Boussinesq equation as given by equation (1).
. We also investigate the modulational instability of such solitary wave solution in the generalized Boussinesq equation. We found out the general condition for which this modulational instability is possible. Finally, we deduce from the general criteria the criteria of modulational instability in the classical Boussinesq equation as given by equation (1).ACKNOWLEDGEMENTS
- I acknowledge support from the ministry of Higher Education of Cameroon through its program of support to Research, which enabled me to carry out this work.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML