-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2015; 5(6): 174-177
doi:10.5923/j.ajcam.20150506.03

Computing the Atom Bond Connectivity and Geometric-Arithmetic Indices of V-Phenylenic Nanotubes and Nanotori
Mohammad Reza Farahani1, M. R. Rajesh Kanna2
1Department of Applied Mathematics of Iran University of Science and Technology (IUST), Narmak, Tehran, Iran
2Post Graduate Department of Mathematics, Maharani's Science College for Women, Mysore, India
Correspondence to: Mohammad Reza Farahani, Department of Applied Mathematics of Iran University of Science and Technology (IUST), Narmak, Tehran, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Let G be a simple connected graph and e=uv be an edge bond of G in chemical graph theory. The Geometric-arithmetic GA index is 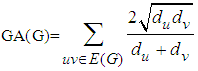 and the Atom-bond connectivity ABC index is defined as
and the Atom-bond connectivity ABC index is defined as 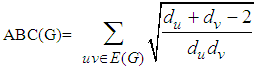 in which degree of a vertex v denoted by dv. In this present study, we compute some results about these connectivity topological indices of V-phenylenic Nanotubes and Nanotori.
in which degree of a vertex v denoted by dv. In this present study, we compute some results about these connectivity topological indices of V-phenylenic Nanotubes and Nanotori.
Keywords: Nanotubes, Molecular graph, Geometric-Arithmetic index, Atom-Bond connectivity index
Cite this paper: Mohammad Reza Farahani, M. R. Rajesh Kanna, Computing the Atom Bond Connectivity and Geometric-Arithmetic Indices of V-Phenylenic Nanotubes and Nanotori, American Journal of Computational and Applied Mathematics , Vol. 5 No. 6, 2015, pp. 174-177. doi: 10.5923/j.ajcam.20150506.03.
1. Introduction
- Let G be a simple connected graph and e=uv be an edge of G in graph theory. A graph is a collection of points and lines connecting a subset of them. The points and lines of a graph also called vertices and edges of the graph, respectively. Also in chemical graph theory, the vertices and edges of a graph also correspond to the atoms and bonds of the molecular graph, respectively. If e is an edge/bond of G, connecting the vertices/atoms u and v, then we write e=uv and say "u and v are adjacent".Chemical graph theory is an important branch of graph theory and Mathematical chemistry, which applies graph theory to mathematical modeling of chemical phenomena [1-6]. A chemical topological index is a numeric quantity from the structural graph of a molecule and is invariant on the automorphism of the graph. One of the important topological connectivity index in chemical graph theory is the Geometric-Arithmetic index GA considered by D. Vukičević and B. Furtula [7] as
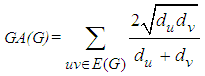 where du and dv are the degrees of the vertices u and v, respectively.Another important connectivity index is the Atom-Bond Connectivity index ABC and was introduced by B. Furtula et al [8] and is defined as follows:
where du and dv are the degrees of the vertices u and v, respectively.Another important connectivity index is the Atom-Bond Connectivity index ABC and was introduced by B. Furtula et al [8] and is defined as follows: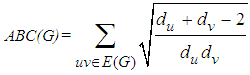 For a comprehensive survey of the mathematical properties and chemical properties of these indices see papers series and books [9-33].In this paper, we focus on the Atom-Bond Connectivity index ABC and the Geometric-Arithmetic index GA and compute some results about these connectivity topological indices for two kind of Nano-structures “V-Phenylenic Nanotubes G=VPHX[m,n] and V-Phenylenic Nanotorus H=VPHY[m,n]”.
For a comprehensive survey of the mathematical properties and chemical properties of these indices see papers series and books [9-33].In this paper, we focus on the Atom-Bond Connectivity index ABC and the Geometric-Arithmetic index GA and compute some results about these connectivity topological indices for two kind of Nano-structures “V-Phenylenic Nanotubes G=VPHX[m,n] and V-Phenylenic Nanotorus H=VPHY[m,n]”.2. Main Results
- The goal of this section is to compute the Atom-Bond Connectivity ABC and the Geometric-Arithmetic GA indices of two carbon Nano-structures. The structure of these two carbon Nano-structures “V-Phenylenic Nanotubes and Nanotorus” are consist of cycles with length four (C4), six (C6) and eight (C8). In other words, in the structure of these nanotubes a C4C6C8 net is a trivalent decoration made by alternating C4, C6 and C8. These can cover either a cylinder or a torus. In Figure 1 and Figure 2, a 2-Dimensional lattice of V-Phenylenic Nanotubes G=VPHX[m,n] and V-Phenylenic Nanotorus H=VPHY[m,n] are shown (∀m,n>1). Let we denote the number of hexagon in the first row of the 2D-lattice of V-Phenylenic G and H by m and alternatively we denote the number of hexagon in the first column by n. From Figures 1 and 2, we see that in each period, there are 6 vertices and we have mn repetition. Thus the number of vertices in V-Phenylenic G and H is equal to |V(VPHX[m,n])|=|V(VPHY[m,n])|=6mn. Since there are m vertices with degree two in the first row and m vertices with degree two in the last row, too and other vertices have degree three, then the number of edges in V-Phenylenic Nanotubes G=VPHX[m,n] (∀m,n>1) is equal to
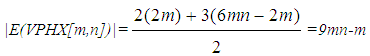 On other hands, since all vertices in V-Phenylenic Nanotorus H=VPHY[m,n] (∀m,n>1), have degree three, thus, |E(VPHY[m,n])|=½×3(6mn)=9mn.For a review, historical details and further bibliography see references [33-42]. Now we compute the ABC and GA indices of the V-Phenylenic Nanotubes and V-Phenylenic Nanotorus by G=VPHX[m,n] and H=VPHY[m,n] (∀m, n∈ℕ-{1}),Theorem 1. Let G be the V-Phenylenic Nanotubes VPHX[m,n] and H be the V-Phenylenic Nanotorus VPHY[m,n] for every m,n∈ℕ-{1}, then• Geometric-Arithmetic index of G is equal to
On other hands, since all vertices in V-Phenylenic Nanotorus H=VPHY[m,n] (∀m,n>1), have degree three, thus, |E(VPHY[m,n])|=½×3(6mn)=9mn.For a review, historical details and further bibliography see references [33-42]. Now we compute the ABC and GA indices of the V-Phenylenic Nanotubes and V-Phenylenic Nanotorus by G=VPHX[m,n] and H=VPHY[m,n] (∀m, n∈ℕ-{1}),Theorem 1. Let G be the V-Phenylenic Nanotubes VPHX[m,n] and H be the V-Phenylenic Nanotorus VPHY[m,n] for every m,n∈ℕ-{1}, then• Geometric-Arithmetic index of G is equal to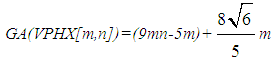 • Atom-Bond Connectivity index of G is equal to
• Atom-Bond Connectivity index of G is equal to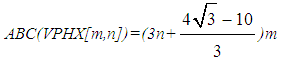 • Geometric-Arithmetic index of H is equal toGA(H)=|E(VPHY[m,n])|=9mn• Atom-Bond Connectivity index of H is equal toABC(H)=|V(VPHY[m,n])|=6mnBefore prove the main results in Theorem 1, let us introduce following definition.Definition 1. [32] For a connected graph G=(V(G),E(G)) with the minimum and maximum of degrees δ=Min{dv|v∈V(G)} and Δ=Max{dv|v∈V(G)}, respectively, there exist vertex.atom and edge/bond partitions as follow∀k: δ≤k≤Δ, Vk={v∈V(G)| dv=k}∀i: 2δ≤i≤2Δ, Ei={e=uv∈E(G)|du+dv=i}∀j: δ2≤j≤Δ2, Ej*={uv∈E(G)|du×dv=j}.Thus, the edge set of V-Phenylenic Nanotubes G=VPHX[m,n] can be dividing to two partitions, e.g. E5 and E6, as follow:• For every e=uv belong to E6, du=dv=3 or E5=E6*={uv∈E(VPHX[m,n])|du+dv=5 & du×dv=6}• For every e=uv belong to E5, then du=2 and dv=3 orE6=E9*={uv∈E(VPHX[m,n])|du+dv=6 & du×dv=9}.Also, all member in edge set of V-Phenylenic Nanotorus VPHY[m,n] exist in a following partition E6 or E9* since all vertices/atoms have degree three.E6=E9*={uv∈E(VPHY[m,n])|du+dv=6& du×dv=9}=E(VPHY[m,n])
• Geometric-Arithmetic index of H is equal toGA(H)=|E(VPHY[m,n])|=9mn• Atom-Bond Connectivity index of H is equal toABC(H)=|V(VPHY[m,n])|=6mnBefore prove the main results in Theorem 1, let us introduce following definition.Definition 1. [32] For a connected graph G=(V(G),E(G)) with the minimum and maximum of degrees δ=Min{dv|v∈V(G)} and Δ=Max{dv|v∈V(G)}, respectively, there exist vertex.atom and edge/bond partitions as follow∀k: δ≤k≤Δ, Vk={v∈V(G)| dv=k}∀i: 2δ≤i≤2Δ, Ei={e=uv∈E(G)|du+dv=i}∀j: δ2≤j≤Δ2, Ej*={uv∈E(G)|du×dv=j}.Thus, the edge set of V-Phenylenic Nanotubes G=VPHX[m,n] can be dividing to two partitions, e.g. E5 and E6, as follow:• For every e=uv belong to E6, du=dv=3 or E5=E6*={uv∈E(VPHX[m,n])|du+dv=5 & du×dv=6}• For every e=uv belong to E5, then du=2 and dv=3 orE6=E9*={uv∈E(VPHX[m,n])|du+dv=6 & du×dv=9}.Also, all member in edge set of V-Phenylenic Nanotorus VPHY[m,n] exist in a following partition E6 or E9* since all vertices/atoms have degree three.E6=E9*={uv∈E(VPHY[m,n])|du+dv=6& du×dv=9}=E(VPHY[m,n])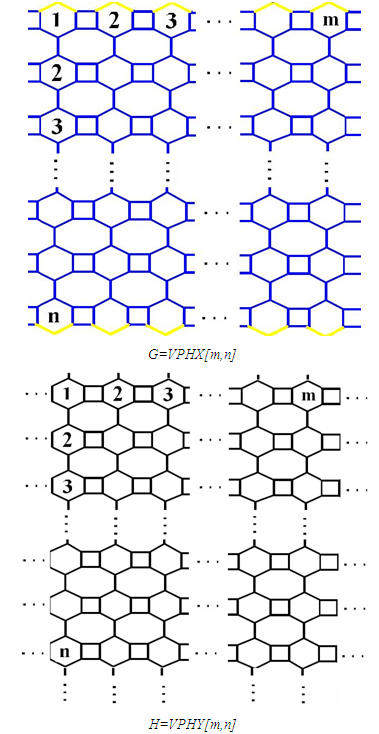 | Figure 1. The 2-Dimensional lattice of V-Phenylenic Nanotubes G=VPHX[m,n] and V-Phenylenic Nanotorus H=VPHY[m,n] |
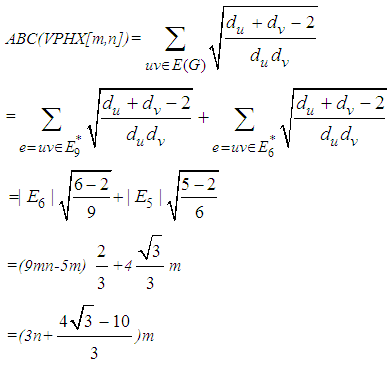
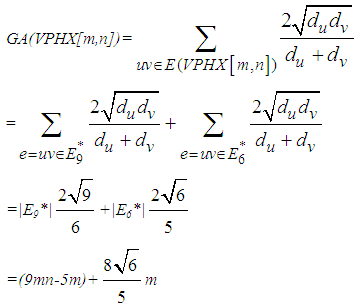 Finally, Consider V-Phenylenic Nanotorus H=VPHY[m,n] with 6mn vertices and 9mn edges. And by according to the 2-Dimensional lattice of H in Figure1, we see that all member of single edge partition E6 (or E9*) are mwrked by black color, such that in H=VPHY[m,n] (∀m,n∈ℕ-{1}), |E6|=|E9*|=9mn=|E(VPHY[m,n])|. Therefore the Atom-Bond Connectivity index ABC and the Geometric-Arithmetic index GA of V-Phenylenic Nanotorus H=VPHY[m,n] are equal to:
Finally, Consider V-Phenylenic Nanotorus H=VPHY[m,n] with 6mn vertices and 9mn edges. And by according to the 2-Dimensional lattice of H in Figure1, we see that all member of single edge partition E6 (or E9*) are mwrked by black color, such that in H=VPHY[m,n] (∀m,n∈ℕ-{1}), |E6|=|E9*|=9mn=|E(VPHY[m,n])|. Therefore the Atom-Bond Connectivity index ABC and the Geometric-Arithmetic index GA of V-Phenylenic Nanotorus H=VPHY[m,n] are equal to: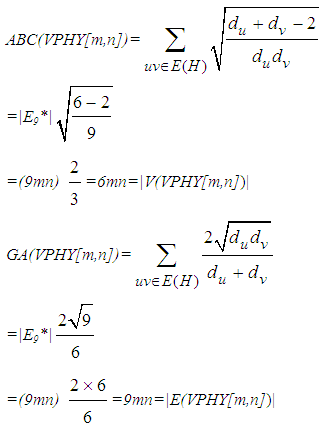 And these completed the proof of theorem.
And these completed the proof of theorem.ACKNOWLEDGEMENTS
- Authors are also thankful to the University Grants Commission, Government of India, for the financial support under the Grant MRP(S)-0535/13-14/KAMY004/ UGC-SWRO.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML