-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2015; 5(6): 164-173
doi:10.5923/j.ajcam.20150506.02

Constitutive Relations of Stress and Strain in Stochastic Finite Element Method
Drakos Stefanos
International Centre for Computational Engineering, Rhodes, Greece
Correspondence to: Drakos Stefanos, International Centre for Computational Engineering, Rhodes, Greece.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The analysis and design in structural and geotechnical engineering problems requires the calculation of stress and strain which is generally a difficult task because of the uncertainty and spatial variability of the properties of soil materials. This paper presents a procedure of conducting Stochastic Finite Element Analysis using Polynomial Chaos in order to propagate the uncertainties of input to constitutive relation of stress and strain. The problem is dominated by highly non linearity. Among other methods the procedure leads to an efficient computational cost for real practical problems. This is achieved by polynomial chaos expansion displacement field, stress and strain also. An example of a plane-strain strip load on a semi-infinite elastic foundation is presented and the results of settlement are compared to those obtained from the closed form solution method. A close matching of the two is observed. The constitutive relation of stress and strain is presented as result of the Polynomial Chaos expansion and Monte Carlo method. A close matching of the two method is observed also.
Keywords: Stochastic Finite Element Method, Constitutive Relations, Polynomial Chaos, Quantification of Uncertainty
Cite this paper: Drakos Stefanos, Constitutive Relations of Stress and Strain in Stochastic Finite Element Method, American Journal of Computational and Applied Mathematics , Vol. 5 No. 6, 2015, pp. 164-173. doi: 10.5923/j.ajcam.20150506.02.
Article Outline
1. Introduction
- The analysis and design in structural and geotechnical engineering problems requires the calculation of stress and strain which is generally a difficult task because of the uncertainty and spatial variability of the materials’s properties. Various forms of uncertainties arise which depend on the nature of geological formation or construction method, the site investigation, the type and the accuracy of design calculations etc. In recent years there has been considerable interest amongst engineers and researchers in the issues related to quantification of uncertainty as it affects safety, design as well as the cost of projects. A number of approaches using statistical concepts have been proposed in engineering in the past 25 years or so. These include the Stochastic Finite Element Method (SFEM) [1-3], and the Random Finite Element Method (RFEM) [4-8]. The RFEM involves generating a random field of soil or structure properties with controlled mean, standard deviation and spatial correlation length, which is then mapped onto a finite element mesh. However the number of works on the stochastic stress and strain calculation and their statistical moments are limited. An essential paper on the field is presented by Ghosh & Farhat [9] where the constitutive relation of stress and strain calculated by different approaches.In the past SFEM has been developed using different expansions of stochastic variables. In this paper we present SFEM [11-13] using the method of Generalized Polynomial Chaos (GPC) [14]. To descretise the stochastic process of material the Karhunen-Loeve Expansion was used and it is presented. The constitutive relation of stress and strain calculated using the Generalized Polynomial Chaos and verified against Monte Carlo simulation which is treated as the exact solution based on a series of computational experiment.A numerical example of foundation settlement given in the last part of the paper and the results of settlement compared with those arises from closed form solution. The two methods of stress and strains constitutive relation compared also and the results are presented.
2. Problem Description and Model Formulation
- Let us consider a general boundary value problem of computation of probable deformation of a body of arbitrary shape having randomly varying material properties caused by the application of a randomly varying load as shown in Fig. 1.
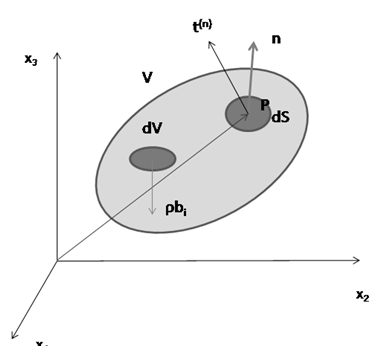 | Figure 1. Body of arbitrary shape |
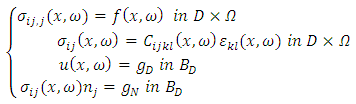 | (1) |
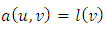 | (2) |
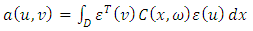 | (3) |
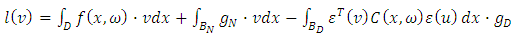 | (4) |
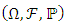 where
where 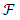 is the σ-algebra and is considered to contain all the information that is available,
is the σ-algebra and is considered to contain all the information that is available, 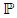 is the probability measure and the spatial domain of the soil or the structure is
is the probability measure and the spatial domain of the soil or the structure is 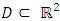 . The Elasticity modulus
. The Elasticity modulus 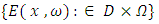 and the external load
and the external load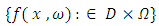 considered as second order random fields and their functions are determined
considered as second order random fields and their functions are determined 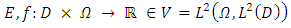 and characterized by specific distribution where in our case as lognormal. Considering as
and characterized by specific distribution where in our case as lognormal. Considering as 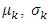 and
and 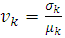 the mean value the standard deviation and the coefficient of variation of Elasticity modulus, the lognormal distribution is given [8]:
the mean value the standard deviation and the coefficient of variation of Elasticity modulus, the lognormal distribution is given [8]: 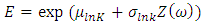 | (5) |
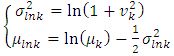 | (6) |
 To separate the deterministic part from the stochastic part of the formulation the Karhunen-Loeve expansion has been used. It is considered as the most efficient method for the discretization of a random field, requiring the smallest number of random variables to represent the field within a given level of accuracy. Based on that the stochastic process of Young modulus over the spatial domain with a known mean value
To separate the deterministic part from the stochastic part of the formulation the Karhunen-Loeve expansion has been used. It is considered as the most efficient method for the discretization of a random field, requiring the smallest number of random variables to represent the field within a given level of accuracy. Based on that the stochastic process of Young modulus over the spatial domain with a known mean value  and covariance matrix
and covariance matrix  assuming lognormal distribution is given by:
assuming lognormal distribution is given by: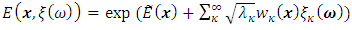 | (7) |
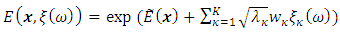 | (8) |
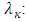 are the eingenvalues of the covariance function
are the eingenvalues of the covariance function 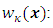 are the eingenfunctions of the covariance function
are the eingenfunctions of the covariance function 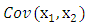
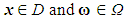
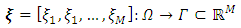 and
and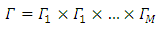 The pairs of eingenvalues and eingenfunctions arised by the equation:
The pairs of eingenvalues and eingenfunctions arised by the equation: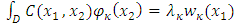 | (9) |
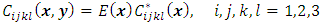 | (10) |
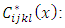 is expressed in terms of (deterministic) Poisson's ratio as
is expressed in terms of (deterministic) Poisson's ratio as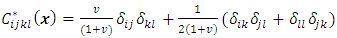 | (11) |
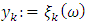 and
and 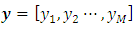 [10]. If the random variables are independent and
[10]. If the random variables are independent and 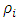 denote the density of
denote the density of 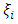 then the joint density is given by:
then the joint density is given by: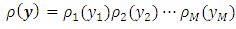 | (12) |
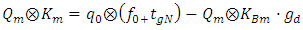 | (13) |
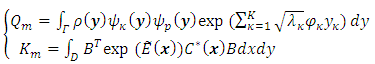 | (14) |
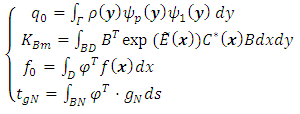 | (15) |
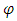 is the hat function.
is the hat function. 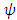 is the Polynomial Chaos
is the Polynomial Chaos3. Constitutive Relations of Stress and Strain
- The calculation of the constitutive relation of stress and strain in the case of stochastic problems is quite complicated especially when the invariant of them are needed where the equations become highly nonlinear. In [9] several numerical integration schemes to evaluate the statistical moments of strains and stresses in a random system is presented. In the current work the propagation of the input uncertainty to the stress and strain relation is modelled by the polynomial Chaos expansion and verified against Monte Carlo simulation which is treated as the exact solution of the problems. The computational implementation of the Monte Carlo Method leads to the random field generation and the requested function
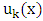 gets a new value for each realization. At the end of all simulations the statistical moment are calculated. The expected value and the variance are given by:
gets a new value for each realization. At the end of all simulations the statistical moment are calculated. The expected value and the variance are given by: 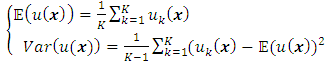 | (16) |
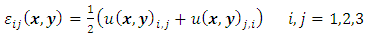 | (17) |
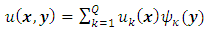 | (18) |
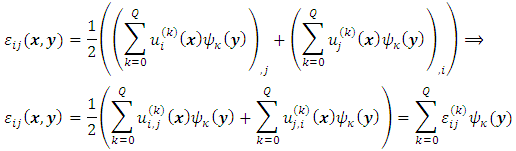 | (19) |
3.1. Expected Value of Strains
- According to the polynomial chaos expansion of strains the expected value can be evaluated by the following:
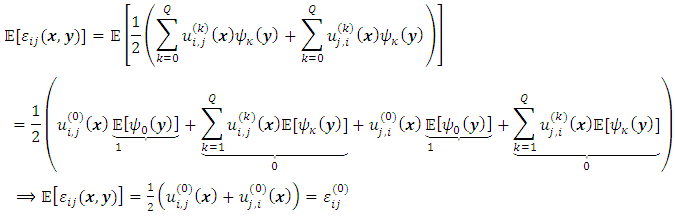 | (20) |
3.2. Variance of Strains
- Respected to the expected value evaluation and the Chaos Polynomial characteristics the variance of the strain tensor can be calculated as:
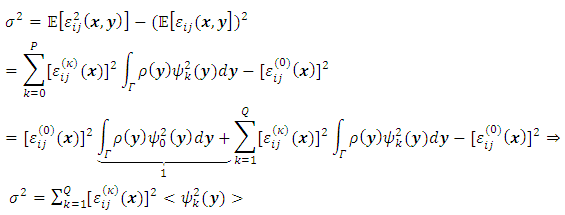 | (21) |
3.3. Expected Value of Stress Tensor
- The constitutive relation of stress and strain given by the well known equation of Hooke’s law equation:
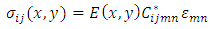 | (22) |
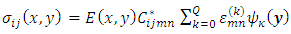 | (23) |
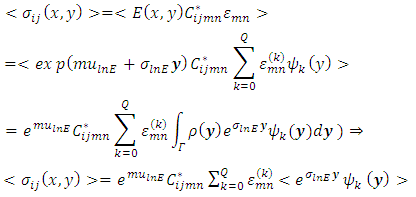 | (24) |
3.4. Variance of Stress Tensor
- Having calculated the expected value of stress tensor and knowing its stochastic equation of by the Hook’s law constitutive relation, the variance of stress tensor can be calculated as:
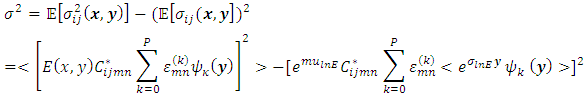 Given the elasticity modulus distribution the variance of stress tensor is equal to:
Given the elasticity modulus distribution the variance of stress tensor is equal to: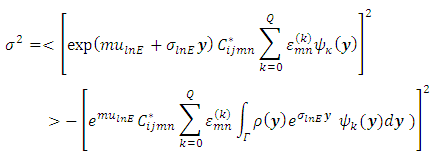 | (25) |
3.5. Pore Pressure Calculation
- A major issue in a wide range of geotechnical and geomechanics problem is the estimation of the excess pore pressure in the ground. Using the Chaos Polynomial expansion the statistical moments of pore pressure can be evaluated as following. The pore pressure is given by the following equation:
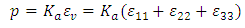 | (25) |
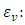 is the volumetric strain
is the volumetric strain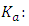 is shown [15] as
is shown [15] as 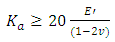 | (26) |
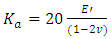
3.5.1. Expected Value of Pore Pressure
- The expected value of pore pressure is the result of the summation of the expected value of the strain’s Chaos expansion multiplied by the stochastic fluid modulus:
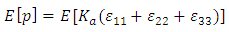 | (27) |
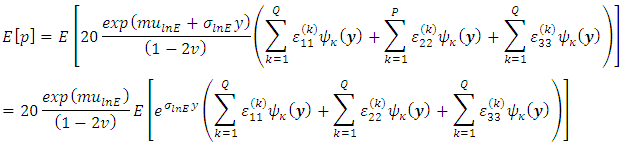 And finally
And finally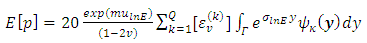 | (28) |
3.5.2. Variance of Pore Pressure
- Using the outcome of the pore pressure expected value its variance is given by:
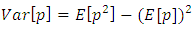 Where:
Where: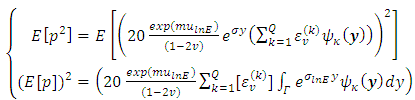 | (29) |
3.6. Invariants of Stress Tensor
- It is well known that to solve engineering problem the model itself should be defined independent of the coordinate system attached to the material. Thus, it is necessary to define the model in terms of stress invariants which are, by definition, independent of the coordinate system selected. The physical content of a stress tensor is reflected exclusively in the stress invariants
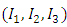 .Where:
.Where: | (30) |
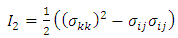 | (31) |
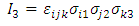 | (32) |
3.6.1. Expected value of I1
- According to the linearity of the excepted value of
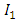 can be calculated:
can be calculated: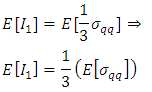 Where:
Where: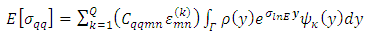 | (33) |
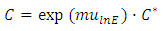 | (34) |
3.6.2. Variance of I1
- Knowing the mean value of
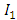 the variance is:
the variance is: But due to linearity:
But due to linearity: Where:
Where: | (35) |
3.6.3. Expected Value of I2
- As shown before:
 This gives
This gives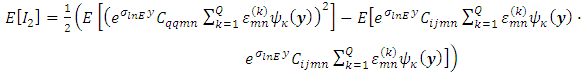 | (36) |
3.6.4. Variance of I2
- The variance of
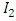 due to the stress product on its equation become highly nonlinear. Thus
due to the stress product on its equation become highly nonlinear. Thus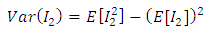 Where:
Where: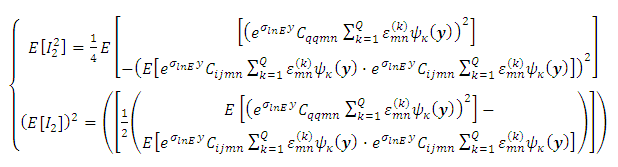 | (37) |
3.6.5. Expected Value of I3
- The high non linearity presented also in the statistical moments of
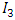 .
.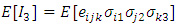 This leads to:
This leads to: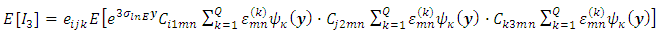 | (38) |
3.6.6. Variance of I3
- Similarly as documented above the variance of
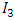 is equal to:
is equal to: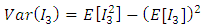 Where:
Where: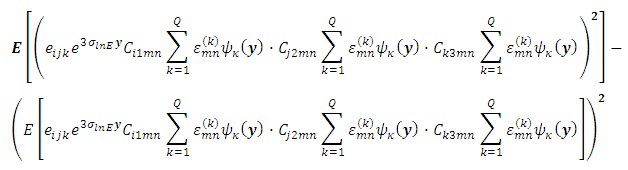 | (39) |
4. Numerical Example
- A shallow foundation problem for various values of variation’s coefficient
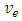 is solved taken to account the randomness of the ground. To estimate the statistical moments of the soil deformation the numerical algorithm of SFEM using the Generalized Polynomial Chaos as described in the previous paragraphs is applied and the results are compared to those obtained by the closed form solution. To avoid the negative values of the elastic modulus assumed to have lognormal. It is known that the settlement beneath a foundation with uniform but random elastic modulus is given by the equation [8]:
is solved taken to account the randomness of the ground. To estimate the statistical moments of the soil deformation the numerical algorithm of SFEM using the Generalized Polynomial Chaos as described in the previous paragraphs is applied and the results are compared to those obtained by the closed form solution. To avoid the negative values of the elastic modulus assumed to have lognormal. It is known that the settlement beneath a foundation with uniform but random elastic modulus is given by the equation [8]: 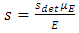 | (40) |
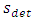 is the deterministic value of settlement with
is the deterministic value of settlement with 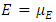 everywhere.Assuming lognormal distribution for the settlements the mean values is equal to
everywhere.Assuming lognormal distribution for the settlements the mean values is equal to 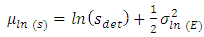 | (41) |
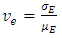 of the elastic modulus with a minimum value of 0.1 and then with step 0.1 to a maximum value equal to 1. The randomness of Elasticity modulus in Fig. 3 is shown. For SFEM one dimensional Hermite GPC with order 5 [14] were used. In the Fig. B1 the results of SFEM method comparatively with the closed form solution are shown and they present great accuracy. It is observed that for of ve = 0.5 the error is equal to 0.8%. In the figures B2-B13 the strains and stress components, the pore pressure and the stress tensor invariants are presented as resulted by the Chaos Polynomial expansion and compared with those raised by the Monte Carlo Method. Simulations of 1000-5000 samples were carried and the convergence of the outcomes decreases as the number of Monte Carlo simulations increases.
of the elastic modulus with a minimum value of 0.1 and then with step 0.1 to a maximum value equal to 1. The randomness of Elasticity modulus in Fig. 3 is shown. For SFEM one dimensional Hermite GPC with order 5 [14] were used. In the Fig. B1 the results of SFEM method comparatively with the closed form solution are shown and they present great accuracy. It is observed that for of ve = 0.5 the error is equal to 0.8%. In the figures B2-B13 the strains and stress components, the pore pressure and the stress tensor invariants are presented as resulted by the Chaos Polynomial expansion and compared with those raised by the Monte Carlo Method. Simulations of 1000-5000 samples were carried and the convergence of the outcomes decreases as the number of Monte Carlo simulations increases. 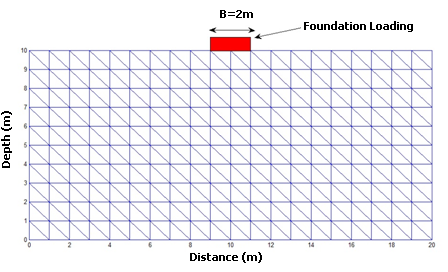 | Figure 2. Finite element mesh |
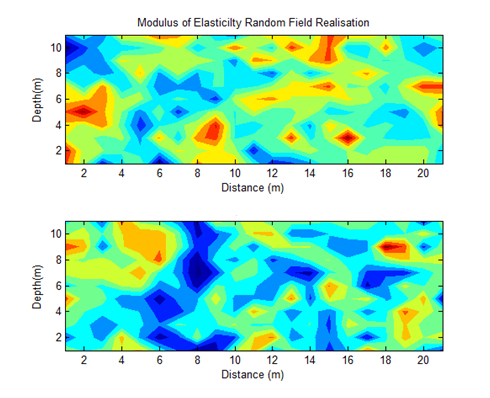 | Figure 3. Modulus of Random Elasticity of two different realizations |
5. Conclusions
- To propagate the uncertainties of input parameters to constitutive relations of strain and stress where arises due to spatial variability of mechanical parameters of soil/rock in geotechnical and geomechanics problems, a procedure of conducting a Stochastic Finite Element Analysis has been presented. An algorithm of Stochastic Finite Element using Polynomial Chaos has been developed. An analysis of settlement of a plane strain strip load on an elastic foundation has been given as an example of the proposed approach. It is shown that the results of SFEM using polynomial chaos compare well with those obtained from closed form solution. The stress and strain constitutive relation the pore pressure and the stress invariants are modeled by the polynomial Chaos expansion and verified against Monte Carlo simulation which is treated as the exact solution of the problems. The main advantage in using the proposed methodology is that a large number of realizations which have to be made for (Random Finite Element Method) avoided, thus making the procedure viable for realistic practical problems.
Appendix A
- Galerkin approximation and Generalized Polynomial of chaos In order to solve the problem 1 we have to create the new space
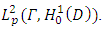 For that reason the subspace
For that reason the subspace 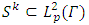 is considered as [10].
is considered as [10].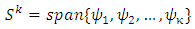 | (A.1) |
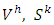 the space
the space 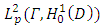 created. Thus
created. Thus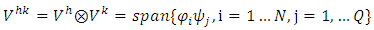 | (A.2) |
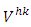 has dimension QN and regards the test function v. In the case where exists
has dimension QN and regards the test function v. In the case where exists 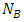 finite element supported by boundaries condition then the subspace of solution belongs is:
finite element supported by boundaries condition then the subspace of solution belongs is: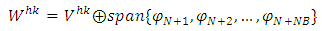 | (A.3) |
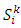 represents a space of univariate orthonormal polynomial of variable
represents a space of univariate orthonormal polynomial of variable 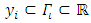 with order k or lower and:
with order k or lower and: 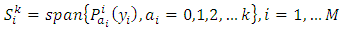 | (A.4) |
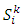 subspace results the space of the Generalized Polynomial Chaos:
subspace results the space of the Generalized Polynomial Chaos: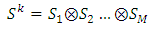 | (A.5) |
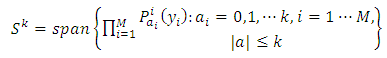 | (A.6) |
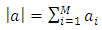 And
And 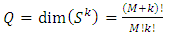 | (A.7) |
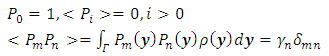 | (A.8) |
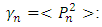 are the normalization factors,
are the normalization factors, 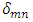 is the Kronecker delta
is the Kronecker delta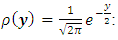 is the density function and
is the density function and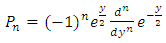 | (A.9) |
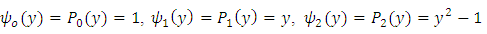
Appendix B
- Results of Numerical Example
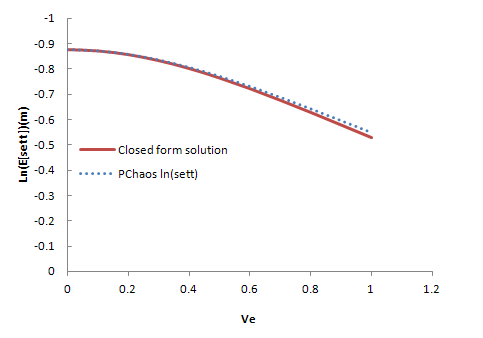 | Figure B1. Closed form solution and SFEM results |
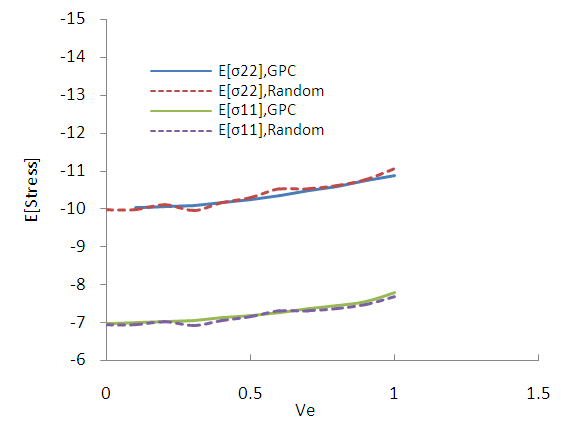 | Figure B2. Expected value of stress tensor complements (MC 1000 samples) |
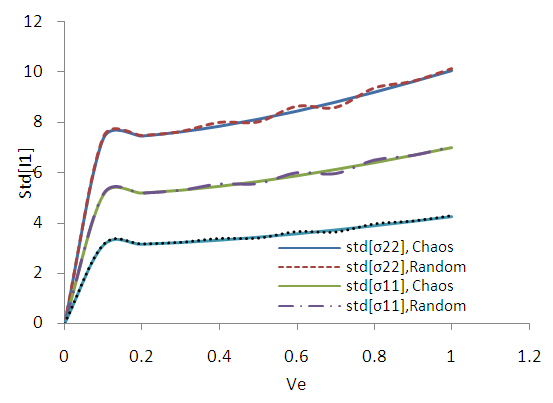 | Figure B3. Standard deviation of stress tensor complements. (MC 1000 samples) |
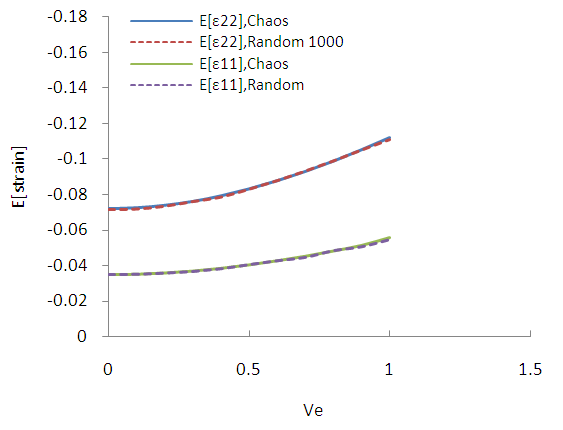 | Figure B4. Expected value of strain tensor complements. (MC 1000 samples) |
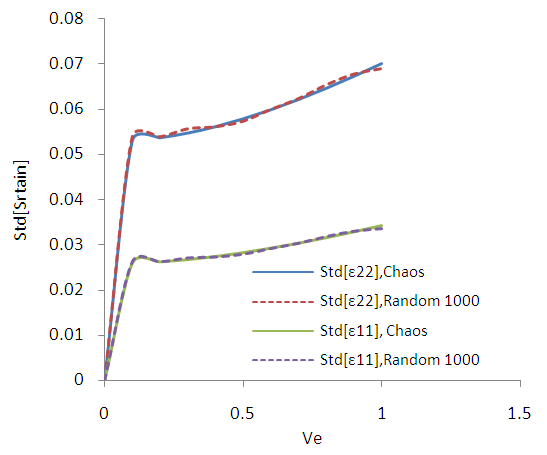 | Figure B5. Standard deviation of strain tensor complements. (MC 1000 samples) |
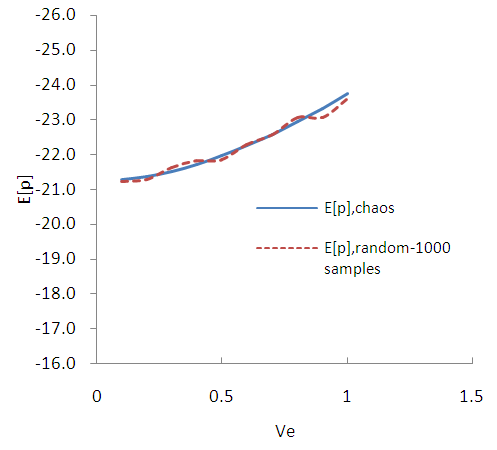 | Figure B6. Expected value of pore pressure. (MC 1000 samples) |
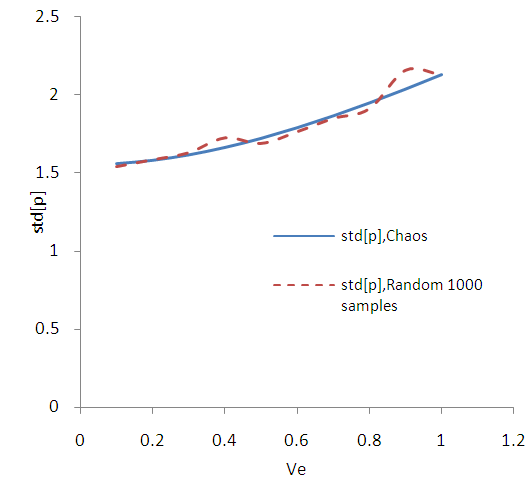 | Figure B7. Standard deviation of pore pressure. (MC 1000 samples) |
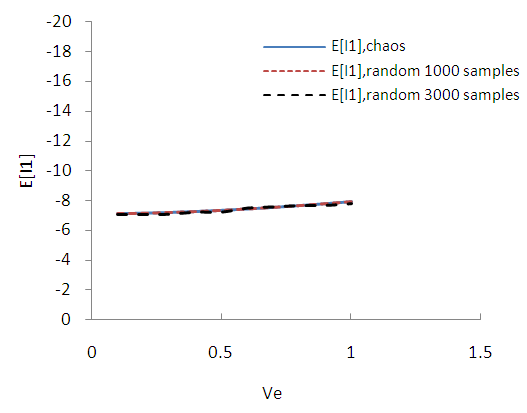 | Figure B8. Expected value of stress tensor invariant I1. (MC 1000, 3000 samples) |
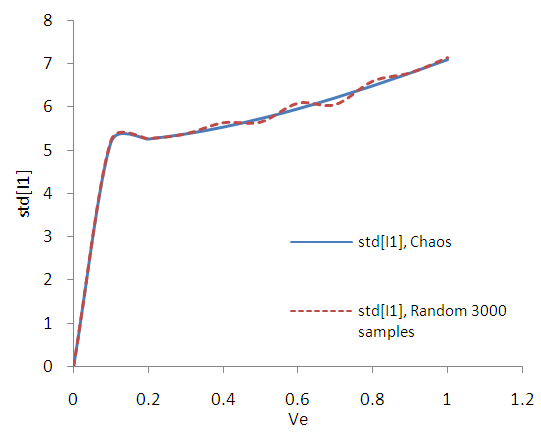 | Figure B9. Standard deviation of stress tensor invariant I1. (MC 3000 samples) |
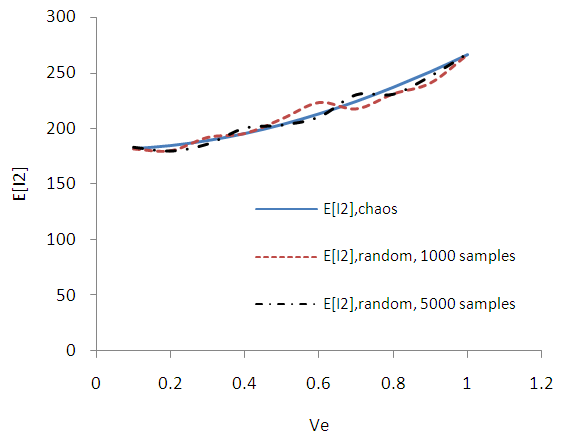 | Figure B10. Expected value of stress tensor invariant I2. (MC 1000, 5000 samples) |
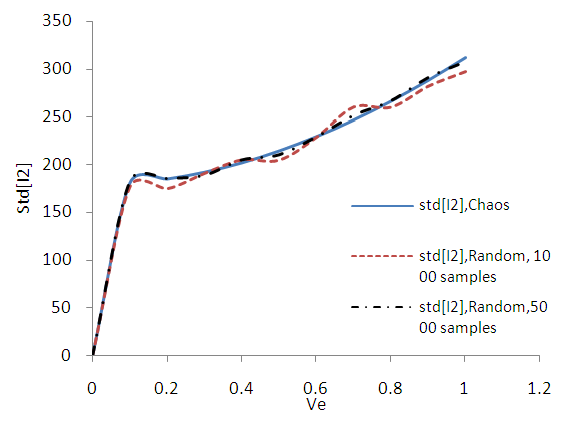 | Figure B11. Standard deviation of stress tensor invariant I2. (MC 1000, 5000 samples) |
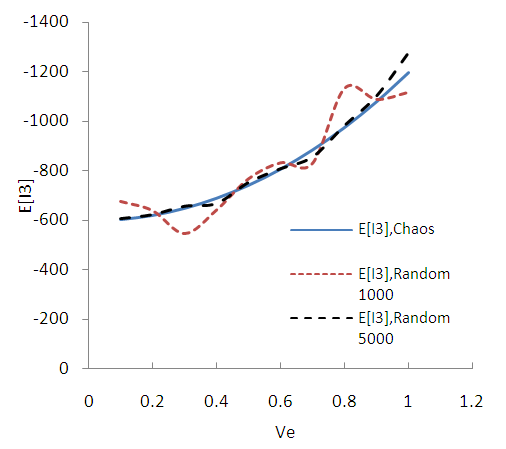 | Figure B12. Expected value of stress tensor invariant I3. (MC 1000, 5000 samples) |
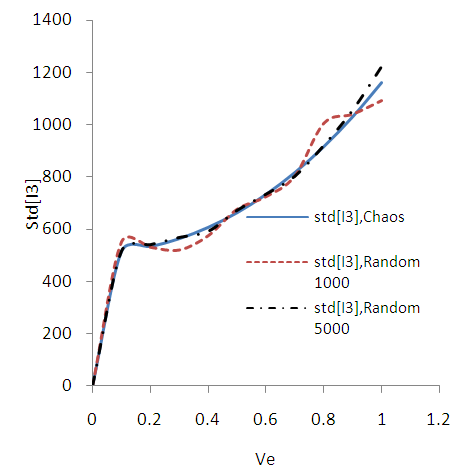 | Figure B13. Standard deviation of stress tensor invariant I3. (MC 1000, 5000 samples) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML