B. Menin
Mechanical & Refrigeration Consultant Expert
Correspondence to: B. Menin, Mechanical & Refrigeration Consultant Expert.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The methodology and exact mathematical calculations of the comparative error of physical-mathematical model that caused only due to finite amount of recorded variables are introduced. This approach allows to reduce time for research and development and to decrease cost of design. The developed concept introduces in the first time a specific metric to estimate the a-priori achievable error for any chosen model before starting computational modeling. Examples of practical application of the considered concept for heat- and mass-transfer processes, measurement of fundamental physical constants and thermal energy storage systems are discussed.
Keywords:
Error Analysis, Fundamental Physical Constants, Heat- and Mass-transfer, Information Theory, Theory of Similarity, Thermal Energy Storage
Cite this paper: B. Menin, Estimation of Required Complexity for Physical-Mathematical Model: Universal Method, American Journal of Computational and Applied Mathematics , Vol. 5 No. 6, 2015, pp. 159-163. doi: 10.5923/j.ajcam.20150506.01.
1. Introduction
Usually, in most scientific publications, it is presupposed that the achievement of high-precision measurements and “low value” of discrepancy between computer results and experimental data testifies the correctness of the proposed physical-mathematical model (PMM). The eligibility choice of PMM is confirmed, in terms of researcher/observer, if the theoretical calculated results coincide with the experimental data within the reached known error of measurements.Nevertheless, errors occur not only during the measurements, but also in a stage of the model synthesis. There are significant errors that arise when developing physical model, mathematical model, in the computer analysis/numerical computations, associated with a finite amount of digits of variables in calculations and, etc.It should me mentioned that the issue of error existing because of a limited number of recorded variables into PMM is generally ignored in the theory of measurements. It covers only a-posteriori error aspects of the measuring procedure and data analysis for the value of the main variable, which describes the observed phenomenon.The well-known and already common in the scientific community point of view is that computer simulations give only the impression of precision, but they are founded on a raft of assumptions, simplifications, and outright errors.All the above mentioned efforts are based on usage of System of Primary Variables (SPV). It is a peculiar channel (generalizing carrier of information) between material object (MO) and conscious observer due to which information is transmitted to researcher or she/he extracts information quantity about the studied phenomena from SPV. As an example of SPV, SI (International system of units), or CGS may be offered.Here we try to introduce the methodology and exact mathematical calculations of the comparative error of PMM that caused only due to limited numbers of observed variables. The applying of the suggested approach can significantly reduce the duration of the research and design phase and thus reduce the cost of the project.
2. The Main Idea
General knowledge about the world is significantly depended on the choice of SPV. It is a set of primary and, designed on their basis, secondary variables [1], which are necessary and sufficient to describe the known nature laws, as in physical content and quantitatively. SPV contains elements as a finite number of physical dimensional (DL) variables which have a potency to characterize the world’s physical properties and, in particular, observed MO qualitatively and quantitatively. So, an observation of MO and the process of modeling are framed by SPV.In turn, SPV includes the primary and secondary variables used for descriptions of different classes of phenomena (COP). In other words, the limits of the description of the studied MO are caused due to the choice of COP and the number of secondary parameters taken into account in the mathematical model [2]. For example, in mechanics SI uses the basis {L– length, M– weight, Т– time}. Basis accounting electromagnetism here adds the strength of electric current I. Thermodynamics requires the inclusion of thermodynamic temperature Θ. For photometry it needs to add J– force of light. The latter basic value of SI is a quantity of substance F. Establishment of a specific SPV (like, for example, SI) means that we are talking about trying to restrict the set of possible variables by a smaller number of basic variables and the corresponding units. Then all the other required variables can be found or determined based on the basic variables.How many different SPV can be built? To answer this question it is necessary to clear what the general properties may be inherent in each SPV. It turns out, that following provisions/ axioms can be formulated [3]. Let the different types of variables (dimensions) are denoted by A, B, C. Then the following relations are realized: a. From A and B a new type of value is built C = A · B (multiplicative relationship); b. There are unnamed numbers, denoted by (1) = (A°), which when multiplied by A do not change the dimensions of this type of variables. A · (1) = A (single item);c. Any type of variables corresponds to the return type of variables 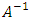 for which
for which 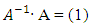 ; d. The relation between the different types of variables is subordinated by: Associativity: A · (B · C) = (A · B) · C, Commutativity: A · B = (B · A); e. For all A ≠ (1) and m∈ N\0 the expression
; d. The relation between the different types of variables is subordinated by: Associativity: A · (B · C) = (A · B) · C, Commutativity: A · B = (B · A); e. For all A ≠ (1) and m∈ N\0 the expression 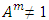 is right;f. The complete set consisting of an infinite number of types of variables has a finite generating system. This means that there is a finite number of elements C1, C2… CH, through which any type of q variable can be represented as
is right;f. The complete set consisting of an infinite number of types of variables has a finite generating system. This means that there is a finite number of elements C1, C2… CH, through which any type of q variable can be represented as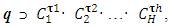 | (1) |
where the badge ﬤ – means "corresponds to dimension"; τi – integer coefficients, 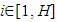 , τi Z, Z is the set of integers.The uniqueness of such representation is not expected in advance.Axioms “a-f” form a complete system of axioms of Abelian group. By taking into account the basic equations of the theory of electricity, magnetism, gravity and thermodynamics, they remain unchanged.Now we use the theorem that is holds for Abelian group: among H elements of the generating system C1, C2… CH there is a subset
, τi Z, Z is the set of integers.The uniqueness of such representation is not expected in advance.Axioms “a-f” form a complete system of axioms of Abelian group. By taking into account the basic equations of the theory of electricity, magnetism, gravity and thermodynamics, they remain unchanged.Now we use the theorem that is holds for Abelian group: among H elements of the generating system C1, C2… CH there is a subset 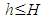 of elements B1, B2… Bh, with the property that each element can be uniquely represented in the form
of elements B1, B2… Bh, with the property that each element can be uniquely represented in the form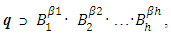 | (2) |
where 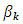 – integers,
– integers, 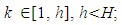 elements
elements 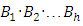 are called the basis of the group, and
are called the basis of the group, and 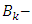 the basic types of variables.
the basic types of variables. 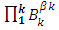 is the product of the dimensions of the main types of variables
is the product of the dimensions of the main types of variables 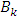 .For the above stated conditions the following statement is fine: the group, which satisfies axioms a-f, has, at least, one basis
.For the above stated conditions the following statement is fine: the group, which satisfies axioms a-f, has, at least, one basis 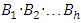 . In the case h> 2, there are infinitely many equal bases. How to determine the number of elements of a basis? In order to answer on this question, let’s apply the approach formulated in [3] for SI. The entire above mentioned can be represented as follows: 1. There are ξ = 7 primary variables: L– length, M– weight, Т– time, I– powered by electric current, Θ– thermodynamic temperature, J– force of light, F– the number of substances [4];2. The dimension of any secondary variable q can only express a unique combination of dimensions of main primary variables in different degrees [1]:
. In the case h> 2, there are infinitely many equal bases. How to determine the number of elements of a basis? In order to answer on this question, let’s apply the approach formulated in [3] for SI. The entire above mentioned can be represented as follows: 1. There are ξ = 7 primary variables: L– length, M– weight, Т– time, I– powered by electric current, Θ– thermodynamic temperature, J– force of light, F– the number of substances [4];2. The dimension of any secondary variable q can only express a unique combination of dimensions of main primary variables in different degrees [1]: 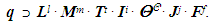 | (3) |
3. l, m... f – integers, the range of each has maximum and minimum value; according to [5] integers are the following: 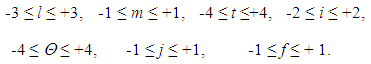 | (4) |
4. The amount of elements of each integer according to (4) is the following: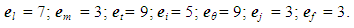 | (5) |
5. The total number of dimension options of physical variables equals 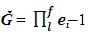
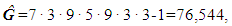 | (6) |
where "-1" corresponds to the occasion when all integers of primary variables in the formula (3) are treated to zero dimension. 6. According to the axiom c, the value 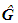 includes both required, and backward variables (for example, L¹ – length, L-1 – running length), so the number of options of dimensions may be reduced in ω = 2 times. It means that the total number of dimension options of physical variables without backward variables equals
includes both required, and backward variables (for example, L¹ – length, L-1 – running length), so the number of options of dimensions may be reduced in ω = 2 times. It means that the total number of dimension options of physical variables without backward variables equals 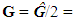
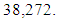 7. According to π-theorem [6], the number
7. According to π-theorem [6], the number 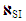 of possible dimensionless (DS) complexes (criteria) with ξ = 7 main dimensional (DL) variables will be
of possible dimensionless (DS) complexes (criteria) with ξ = 7 main dimensional (DL) variables will be 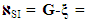
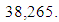 The transition from DL physical quantities to the complex DS variables, which are composed of the same quantities, allows reducing of the number of variables. In addition, it is caused by the desire to generalize obtained results in the future for the different areas of physical applications. The numerical value of
The transition from DL physical quantities to the complex DS variables, which are composed of the same quantities, allows reducing of the number of variables. In addition, it is caused by the desire to generalize obtained results in the future for the different areas of physical applications. The numerical value of 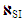 can only increase with the deepening of knowledge about the material world. It should be mentioned that set of DS variables
can only increase with the deepening of knowledge about the material world. It should be mentioned that set of DS variables 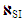 is a fictitious system, since it does not exist in the physical reality. At the same time, the actually existing MO may be expressed by this set.The relationships (3) - (6) are obtained on the basis of the axioms set forth in [3], and the principles of the theory of groups. The present results provide a basis for use of information theory in application to thermodynamic with a view to formulating precise mathematical relationships to assess the minimum comparative error of PMM that describes the studied physical phenomenon or process.
is a fictitious system, since it does not exist in the physical reality. At the same time, the actually existing MO may be expressed by this set.The relationships (3) - (6) are obtained on the basis of the axioms set forth in [3], and the principles of the theory of groups. The present results provide a basis for use of information theory in application to thermodynamic with a view to formulating precise mathematical relationships to assess the minimum comparative error of PMM that describes the studied physical phenomenon or process.
3. Applied Tools
We suppose that the observed/recorded variables are random in terms of information complexity in SPV and each recorded variable is considered as a kind of readout [7]. This allows the conscious observer to get a certain amount of information about the studied MO in the frame of the chosen SPV (in our case, SI). The total number of variables/readouts can be calculated 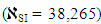 , and it corresponds to the maximum amount of information contained in the SPV. It should be taken into account that the appearance (registration) of readouts is equiprobably. In addition, in the frame work of the suggested approach the human evaluation of information is completely ignored. Based on these assumptions, the lowest DS error
, and it corresponds to the maximum amount of information contained in the SPV. It should be taken into account that the appearance (registration) of readouts is equiprobably. In addition, in the frame work of the suggested approach the human evaluation of information is completely ignored. Based on these assumptions, the lowest DS error 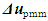 of PMM caused by the finite number of recorded variables can be obtained [8]
of PMM caused by the finite number of recorded variables can be obtained [8]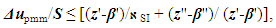 | (7) |
where 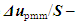 comparative error [7];S - DS interval of observation/supervision of DS variable u;z' – the number of physical DL variables in the selected COP;β' – the number of primary physical DL variables in the selected COP;z" – the number of physical DL variables recorded in physical-mathematical model (PMM); β" – the number of primary physical DL variables of the total number of variables recorded in PMM.The Equation (7) is correct for DL variable U as
comparative error [7];S - DS interval of observation/supervision of DS variable u;z' – the number of physical DL variables in the selected COP;β' – the number of primary physical DL variables in the selected COP;z" – the number of physical DL variables recorded in physical-mathematical model (PMM); β" – the number of primary physical DL variables of the total number of variables recorded in PMM.The Equation (7) is correct for DL variable U as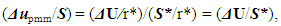 | (8) |
where 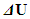 – error in determining the DL variable U; S*- DL range of values in which the DL variable U is measured/changed; r* - DL scale parameter with the same dimension that U and S* have.Factually, Equation (8) can be introduced as an uncertainty principle for the process of PMM formulation. Namely, any change in the level of detailed description of
– error in determining the DL variable U; S*- DL range of values in which the DL variable U is measured/changed; r* - DL scale parameter with the same dimension that U and S* have.Factually, Equation (8) can be introduced as an uncertainty principle for the process of PMM formulation. Namely, any change in the level of detailed description of 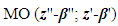 causes a change in the comparative error of
causes a change in the comparative error of 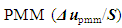 , and in the accuracy calculation of each main variable characterizing the features of the internal structure of MO or the interaction of MO with the environment.
, and in the accuracy calculation of each main variable characterizing the features of the internal structure of MO or the interaction of MO with the environment.
4. Application Studies
In a lot of scientific publications the sufficient basic data needed for the calculation and verification of the results obtained by the equation (7) are not provided.In most cases, there is not factually and simultaneously provided the information about the value of the resulting total uncertainty and about the changes range of the main variable characterizing the studied MO. At this moment, here we attempt to analyze the known results and compare them with the data obtained according to the introduced approach.
4.1. Heat- and Mass-Transfer
The heat transfer to a thin layer of paste and minced-shaped material that is frozen on a moving cooled cylindrical wall is researched [9]. Due to analyzing of recorded variables dimensions, PMM is classified with COP 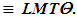 Based on (4) and (5), we find
Based on (4) and (5), we find 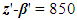 . For this COP and following (4) – (6), the lowest comparative error can be reached at 19 DS variables.There were recorded 18 (z*) input DL parameters and 5 (β*) primary physical variables, then there are z*- β* = 18-5 = 13 DS criteria. The study of the developed PMM by computer experiment [10] realized with usage of random balance method [11] was conducted. As the objective function, the final DS temperature of the outer surface of the material
. For this COP and following (4) – (6), the lowest comparative error can be reached at 19 DS variables.There were recorded 18 (z*) input DL parameters and 5 (β*) primary physical variables, then there are z*- β* = 18-5 = 13 DS criteria. The study of the developed PMM by computer experiment [10] realized with usage of random balance method [11] was conducted. As the objective function, the final DS temperature of the outer surface of the material 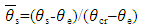 was selected, where
was selected, where 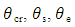 are the DL temperatures, respectively, of freezing of a material, outer surface of a material layer and evaporating of the refrigerant.
are the DL temperatures, respectively, of freezing of a material, outer surface of a material layer and evaporating of the refrigerant. 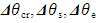 are the DL errors of measurement of these temperatures. Then, one considers
are the DL errors of measurement of these temperatures. Then, one considers 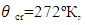
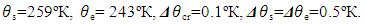 The achieved discrepancy between the experimental and computational data in the range of admissible values of the similarity criteria and dimensionless conversion factors did not exceed 8%.There was taken into account that the direct measurement errors are much smaller than the measured values, accounting for a few percent or less of them. The error can be considered formally as small increments of a measured variable. In practice, finite differences are used, rather than the differentials. So, in order to find the value of an absolute DS error
The achieved discrepancy between the experimental and computational data in the range of admissible values of the similarity criteria and dimensionless conversion factors did not exceed 8%.There was taken into account that the direct measurement errors are much smaller than the measured values, accounting for a few percent or less of them. The error can be considered formally as small increments of a measured variable. In practice, finite differences are used, rather than the differentials. So, in order to find the value of an absolute DS error 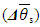 , the mathematical apparatus of differential calculus was applied [12]:
, the mathematical apparatus of differential calculus was applied [12]: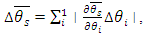 | (9) |
where 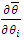 – partial derivatives of the function
– partial derivatives of the function 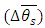 with respect to one of the several variables
with respect to one of the several variables 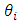 that affect
that affect 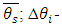 the uncertainty or error.For the present example, according to Equation (9), one can find an absolute total DS error of the indirect measurement
the uncertainty or error.For the present example, according to Equation (9), one can find an absolute total DS error of the indirect measurement 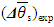 , reached in the experiment:
, reached in the experiment: 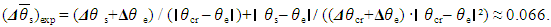 | (10) |
From Equation (7), using calculated values 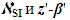 , one gets a DS error value
, one gets a DS error value 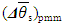 for the chosen PMM:
for the chosen PMM: 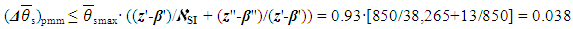 | (11) |
where 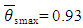 is a given range of changes of the DS final temperature [9] allowed by the chosen PMM. From (10) and (11), we get
is a given range of changes of the DS final temperature [9] allowed by the chosen PMM. From (10) and (11), we get 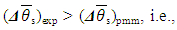 an actual error in the experiment is 1.7 times (0.066/0.038) more than the possible minimum. It means, at the chosen number of DS criteria the existing accuracy of DL variable’s measurement is not enough. In addition, the number of the recorded DS variables z*-β*=13 is less than the recommended ≈19 that corresponds to the lowest comparative error. For further experimental work it is required to use devices of a higher class of accuracy sufficient to confirm/clarify a new PMM designed with lots of DS variables.In this example there is introduced a full explanation of the required steps in order to analyze experimental data and to compare it with results obtained by computer realization of PMM.
an actual error in the experiment is 1.7 times (0.066/0.038) more than the possible minimum. It means, at the chosen number of DS criteria the existing accuracy of DL variable’s measurement is not enough. In addition, the number of the recorded DS variables z*-β*=13 is less than the recommended ≈19 that corresponds to the lowest comparative error. For further experimental work it is required to use devices of a higher class of accuracy sufficient to confirm/clarify a new PMM designed with lots of DS variables.In this example there is introduced a full explanation of the required steps in order to analyze experimental data and to compare it with results obtained by computer realization of PMM.
4.2. Fine Structure Constant
4.2.1. In [13] authors reported a new experimental scheme which combines atom interferometry with Bloch oscillations that leading to a new determination of the fine structure constant 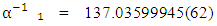 with a relative uncertainty r₁ of
with a relative uncertainty r₁ of 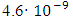 . It means that absolute uncertainty is
. It means that absolute uncertainty is 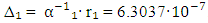 . The declared range S₁ of
. The declared range S₁ of 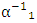 variations is
variations is 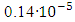 (see Fig. 4, [13]). Research is organized into the frame of COPSI ≡ LMТ. One can calculate the achieved comparative error
(see Fig. 4, [13]). Research is organized into the frame of COPSI ≡ LMТ. One can calculate the achieved comparative error 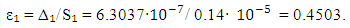 | (12) |
For the mechanics processes (COPSI ≡ LMТ), taking into account [8], the lowest comparative error can be reached at the following conditions: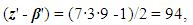 | (13) |
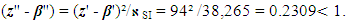 | (14) |
And it equals 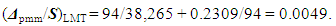 | (15) |
The obtained comparative error ε₁ = 0.4503 is much higher than the recommended (see Equation (15)) according to the discussed approach. So, the above mentioned method and apparatus need to verify the fine structure constant value with a better accuracy.4.2.2. There are a recoil-velocity measurement of Rubidium and new determination of the fine structure constant 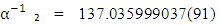 with a relative uncertainty
with a relative uncertainty 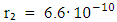 [14]. It means that absolute uncertainty is
[14]. It means that absolute uncertainty is 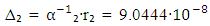 . Following the description of the experimental unit and methods, COPSI ≡ LMТ. According to Equation (15), the lowest comparative error equals 0.0049. The range of variations S₂ of
. Following the description of the experimental unit and methods, COPSI ≡ LMТ. According to Equation (15), the lowest comparative error equals 0.0049. The range of variations S₂ of 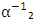 is
is 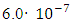 (see Fig.1, [14]). In this case, the comparative error of the experimental method will be
(see Fig.1, [14]). In this case, the comparative error of the experimental method will be 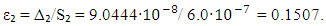 | (16) |
This value is larger than the lowest comparative error for COPSI ≡ LMТ calculated according to Equation (15). That is the reason the research team knows the limit value of the achievable accuracy and can try to find more perspective method for reaching the best results.Two above-stated studies differ from each other by the design of experimental facilities and methods of measurement. However, in the framework of the suggested approach it can be argued that a greater accuracy in the measurement of the fine structure constant was achieved in [14]. This conclusion is possible due the comparison of the value of the comparative errors made in these studies, with the comparative error that was chosen in accordance with the recommended approach and is calculated for the particular class of phenomena COPSI ≡ LMТ.
4.3. Thermal Energy Storage Systems
The similarity theory was applied for three types of energy storage systems [15]. The generalized governing equations and charts bearing curves for energy storage effectiveness against 4 (four) DS criteria were introduced. Total amount of DL variables is 45 including geometric, fluid and thermal storage material properties, as well as the operational conditions. Total amount of DS criteria and numbers used for analyzing working modes was 18. According to the modeler’s allegations, the built charts can help to design and calibrate the size of thermal storage tanks and operational conditions. At the same time, any validation or verification procedures and the comparison with experimental data were absent. By analyzing of dimensions of recorded variables, COP ≡ LMTΘ. According to Equations (4), (5) and (7), for SI and the chosen COPSI ≡ LMTΘ, a lowest comparative error can be reached at 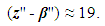 | (17) |
This value is closed to the number of DS criteria used in the reviewed article. It allows supposing that the constructed charts are reliable. More, than this if the spread of the experimental data in comparison with the results of computer simulation is in the range allowed by the researchers, it can be assumed that the selected PMM adequately describes the observed process.So, the introduced approach allows to conscious observer to find, during several minutes, the lowest value of the required/achievable experimental error in order to confirm the expediency of the chosen PMM. This error will correspond to the error inherent in the model and caused only by its finiteness (limited amount of recorded variables).
5. Conclusions
1. To the best knowledge of author, none of the studies or procedures, known to scientific community, sufficiently defines recommendations in order to achieve the highest accuracy or lowest discrepancy between the formulated physical-mathematical model and observed phenomena. Nonetheless, the developed concept allows for the first time to introduce a specific metric to estimate the a-priori achievable error for each formulated physical-mathematical model before starting computational modeling. Factually, this error is the "firstborn" uncertainty inherent to PMM after the choosing of recorded variables by the conscious observer.2. For the user of the methodology developed in this research, we are proposing a method of defining the uncertainty limits for each given particular case.3. Once the conscious observer selects his/her preferences and requirements for the chosen model, a recommendation on what level accuracy of the measurement equipment to monitor, can be provided.4. During carrying out numerical experiments using the theory of planning experiment on computers, the error Δpmm calculated according to the described approach, can also be used. The feasibility of this approach is dictated by the need to calculate the reproducibility dispersion and the Fisher criterion. In turn, the Fisher criterion determines the times of cessation of screening influencing factors, which are important in the study.5. The research approach discussed in this paper can be further refined by analyzing more datasets from actual physical and technological areas and of additional types of physical-mathematical models. The numerous other physical phenomena and industrial cases were not investigated in this research and could form a potential study for the future. 6. Within the proposed approach, the most attractive model describing a material object, on one hand, has the lowest comparative error that is calculated according to (7), on another hand, as possible, retains the details that are necessary to approach the specific goal function by which model is designed to examine.
References
| [1] | A.A. Guhman, Introduction in the Theory of Similarity. Moscow, Russia: High School, 1973, in Russian. |
| [2] | L. I. Sedov, Similarity and Dimensional Methods in Mechanic. 10th ed., USA: CRC Press, 1993. |
| [3] | R. Fleischmann, Einführung in die Physik. Germany: Verlag Chemie GmbH, Physik Verlag, 1973, in German. |
| [4] | IST Special Publication 330 (SP330), the International System of Units (SI), 2008. Available:http://goo.gl/4mcVwX. |
| [5] | B. M. Javorskij and A. A. Detlaf, Reference Book of the Physics. Moscow, Russia: Nauka, 1977, in Russian. |
| [6] | L. Yarin, The Pi-Theorem, Experimental Fluid Mechanics. Berlin Heidelberg, Germany: Springer-Verlag, 2012. Available: https://goo.gl/dtNq3D. |
| [7] | L. Brillouin, Science and Information Theory. New York, USA: USA Dover, 2004. |
| [8] | B. M. Menin, 2014, Comparative error of the phenomena model, International Referred Journal of Engineering and Science, 3(11), 68-76. Available: http://goo.gl/zMtMAU. |
| [9] | B. M. Menin, Drum Freezers: Computer simulation and applications. Germany: Lambert Academic Publishing, 2014. |
| [10] | K. Hartman, E. Letsky, and V. Schaefer, Planning experiment in the study of processes. Moscow, Russia: Mir, 1977, in Russian. |
| [11] | V. Nalimov and N. A. Chernova, Statistical methods for planning of extreme experiments. Moscow, Russia: Nauka, 1965, in Russian. |
| [12] | J. Taylor, An Introduction to Error Analysis, 2nd ed., California, USA: University Science Books, 1982. Available: http://goo.gl/EWbb2r. |
| [13] | M. Cadoret, E. Mirandes, P. Clade, S. Gurlatti-Khelifa, C. Schwob, F. Nez, L. Julien, and F. Biraben F., 2008, Combination of Bloch oscillations with a Ramsey-Borde interferometer: new determination of the fine structure constant, Phys. Rev. Lett., 101, 230801. Available: http://goo.gl/sMF4tg. |
| [14] | R. Bouchendira, P. Clade, S. Gurlatti-Khelifa, F. Nez, and F. Biraben, 2011, New determination of the fine structure constant and test of the quantum electrodynamics, Phys. Rev. Lett., 106, 080801. Available: http://goo.gl/mKatGo. |
| [15] | P. Li, J. Lew, C. Chan, W. Karaki, J. Stephens, and J. O’brien, 2012, Similarity and generalized analysis of efficiencies of thermal energy storage systems, Renewable Energy, 39, 388-402. Available: https://goo.gl/70hM55. |


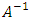 for which
for which 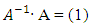 ; d. The relation between the different types of variables is subordinated by: Associativity: A · (B · C) = (A · B) · C, Commutativity: A · B = (B · A); e. For all A ≠ (1) and m∈ N\0 the expression
; d. The relation between the different types of variables is subordinated by: Associativity: A · (B · C) = (A · B) · C, Commutativity: A · B = (B · A); e. For all A ≠ (1) and m∈ N\0 the expression 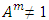 is right;f. The complete set consisting of an infinite number of types of variables has a finite generating system. This means that there is a finite number of elements C1, C2… CH, through which any type of q variable can be represented as
is right;f. The complete set consisting of an infinite number of types of variables has a finite generating system. This means that there is a finite number of elements C1, C2… CH, through which any type of q variable can be represented as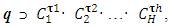
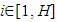 , τi Z, Z is the set of integers.The uniqueness of such representation is not expected in advance.Axioms “a-f” form a complete system of axioms of Abelian group. By taking into account the basic equations of the theory of electricity, magnetism, gravity and thermodynamics, they remain unchanged.Now we use the theorem that is holds for Abelian group: among H elements of the generating system C1, C2… CH there is a subset
, τi Z, Z is the set of integers.The uniqueness of such representation is not expected in advance.Axioms “a-f” form a complete system of axioms of Abelian group. By taking into account the basic equations of the theory of electricity, magnetism, gravity and thermodynamics, they remain unchanged.Now we use the theorem that is holds for Abelian group: among H elements of the generating system C1, C2… CH there is a subset 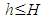 of elements B1, B2… Bh, with the property that each element can be uniquely represented in the form
of elements B1, B2… Bh, with the property that each element can be uniquely represented in the form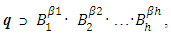
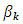 – integers,
– integers, 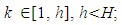 elements
elements 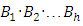 are called the basis of the group, and
are called the basis of the group, and 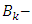 the basic types of variables.
the basic types of variables. 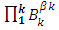 is the product of the dimensions of the main types of variables
is the product of the dimensions of the main types of variables 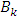 .For the above stated conditions the following statement is fine: the group, which satisfies axioms a-f, has, at least, one basis
.For the above stated conditions the following statement is fine: the group, which satisfies axioms a-f, has, at least, one basis 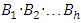 . In the case h> 2, there are infinitely many equal bases. How to determine the number of elements of a basis? In order to answer on this question, let’s apply the approach formulated in [3] for SI. The entire above mentioned can be represented as follows: 1. There are ξ = 7 primary variables: L– length, M– weight, Т– time, I– powered by electric current, Θ– thermodynamic temperature, J– force of light, F– the number of substances [4];2. The dimension of any secondary variable q can only express a unique combination of dimensions of main primary variables in different degrees [1]:
. In the case h> 2, there are infinitely many equal bases. How to determine the number of elements of a basis? In order to answer on this question, let’s apply the approach formulated in [3] for SI. The entire above mentioned can be represented as follows: 1. There are ξ = 7 primary variables: L– length, M– weight, Т– time, I– powered by electric current, Θ– thermodynamic temperature, J– force of light, F– the number of substances [4];2. The dimension of any secondary variable q can only express a unique combination of dimensions of main primary variables in different degrees [1]: 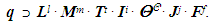
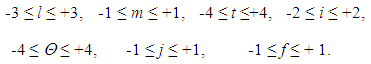
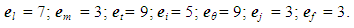
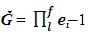
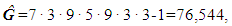
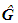 includes both required, and backward variables (for example, L¹ – length, L-1 – running length), so the number of options of dimensions may be reduced in ω = 2 times. It means that the total number of dimension options of physical variables without backward variables equals
includes both required, and backward variables (for example, L¹ – length, L-1 – running length), so the number of options of dimensions may be reduced in ω = 2 times. It means that the total number of dimension options of physical variables without backward variables equals 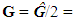
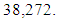 7. According to π-theorem [6], the number
7. According to π-theorem [6], the number 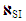 of possible dimensionless (DS) complexes (criteria) with ξ = 7 main dimensional (DL) variables will be
of possible dimensionless (DS) complexes (criteria) with ξ = 7 main dimensional (DL) variables will be 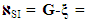
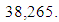 The transition from DL physical quantities to the complex DS variables, which are composed of the same quantities, allows reducing of the number of variables. In addition, it is caused by the desire to generalize obtained results in the future for the different areas of physical applications. The numerical value of
The transition from DL physical quantities to the complex DS variables, which are composed of the same quantities, allows reducing of the number of variables. In addition, it is caused by the desire to generalize obtained results in the future for the different areas of physical applications. The numerical value of 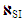 can only increase with the deepening of knowledge about the material world. It should be mentioned that set of DS variables
can only increase with the deepening of knowledge about the material world. It should be mentioned that set of DS variables 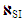 is a fictitious system, since it does not exist in the physical reality. At the same time, the actually existing MO may be expressed by this set.The relationships (3) - (6) are obtained on the basis of the axioms set forth in [3], and the principles of the theory of groups. The present results provide a basis for use of information theory in application to thermodynamic with a view to formulating precise mathematical relationships to assess the minimum comparative error of PMM that describes the studied physical phenomenon or process.
is a fictitious system, since it does not exist in the physical reality. At the same time, the actually existing MO may be expressed by this set.The relationships (3) - (6) are obtained on the basis of the axioms set forth in [3], and the principles of the theory of groups. The present results provide a basis for use of information theory in application to thermodynamic with a view to formulating precise mathematical relationships to assess the minimum comparative error of PMM that describes the studied physical phenomenon or process. 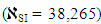 , and it corresponds to the maximum amount of information contained in the SPV. It should be taken into account that the appearance (registration) of readouts is equiprobably. In addition, in the frame work of the suggested approach the human evaluation of information is completely ignored. Based on these assumptions, the lowest DS error
, and it corresponds to the maximum amount of information contained in the SPV. It should be taken into account that the appearance (registration) of readouts is equiprobably. In addition, in the frame work of the suggested approach the human evaluation of information is completely ignored. Based on these assumptions, the lowest DS error 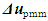 of PMM caused by the finite number of recorded variables can be obtained [8]
of PMM caused by the finite number of recorded variables can be obtained [8]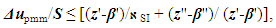
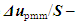 comparative error [7];S - DS interval of observation/supervision of DS variable u;z' – the number of physical DL variables in the selected COP;β' – the number of primary physical DL variables in the selected COP;z" – the number of physical DL variables recorded in physical-mathematical model (PMM); β" – the number of primary physical DL variables of the total number of variables recorded in PMM.The Equation (7) is correct for DL variable U as
comparative error [7];S - DS interval of observation/supervision of DS variable u;z' – the number of physical DL variables in the selected COP;β' – the number of primary physical DL variables in the selected COP;z" – the number of physical DL variables recorded in physical-mathematical model (PMM); β" – the number of primary physical DL variables of the total number of variables recorded in PMM.The Equation (7) is correct for DL variable U as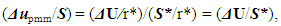
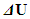 – error in determining the DL variable U; S*- DL range of values in which the DL variable U is measured/changed; r* - DL scale parameter with the same dimension that U and S* have.Factually, Equation (8) can be introduced as an uncertainty principle for the process of PMM formulation. Namely, any change in the level of detailed description of
– error in determining the DL variable U; S*- DL range of values in which the DL variable U is measured/changed; r* - DL scale parameter with the same dimension that U and S* have.Factually, Equation (8) can be introduced as an uncertainty principle for the process of PMM formulation. Namely, any change in the level of detailed description of 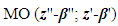 causes a change in the comparative error of
causes a change in the comparative error of 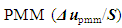 , and in the accuracy calculation of each main variable characterizing the features of the internal structure of MO or the interaction of MO with the environment.
, and in the accuracy calculation of each main variable characterizing the features of the internal structure of MO or the interaction of MO with the environment. 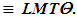 Based on (4) and (5), we find
Based on (4) and (5), we find 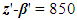 . For this COP and following (4) – (6), the lowest comparative error can be reached at 19 DS variables.There were recorded 18 (z*) input DL parameters and 5 (β*) primary physical variables, then there are z*- β* = 18-5 = 13 DS criteria. The study of the developed PMM by computer experiment [10] realized with usage of random balance method [11] was conducted. As the objective function, the final DS temperature of the outer surface of the material
. For this COP and following (4) – (6), the lowest comparative error can be reached at 19 DS variables.There were recorded 18 (z*) input DL parameters and 5 (β*) primary physical variables, then there are z*- β* = 18-5 = 13 DS criteria. The study of the developed PMM by computer experiment [10] realized with usage of random balance method [11] was conducted. As the objective function, the final DS temperature of the outer surface of the material 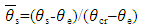 was selected, where
was selected, where 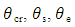 are the DL temperatures, respectively, of freezing of a material, outer surface of a material layer and evaporating of the refrigerant.
are the DL temperatures, respectively, of freezing of a material, outer surface of a material layer and evaporating of the refrigerant. 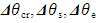 are the DL errors of measurement of these temperatures. Then, one considers
are the DL errors of measurement of these temperatures. Then, one considers 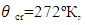
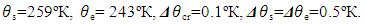 The achieved discrepancy between the experimental and computational data in the range of admissible values of the similarity criteria and dimensionless conversion factors did not exceed 8%.There was taken into account that the direct measurement errors are much smaller than the measured values, accounting for a few percent or less of them. The error can be considered formally as small increments of a measured variable. In practice, finite differences are used, rather than the differentials. So, in order to find the value of an absolute DS error
The achieved discrepancy between the experimental and computational data in the range of admissible values of the similarity criteria and dimensionless conversion factors did not exceed 8%.There was taken into account that the direct measurement errors are much smaller than the measured values, accounting for a few percent or less of them. The error can be considered formally as small increments of a measured variable. In practice, finite differences are used, rather than the differentials. So, in order to find the value of an absolute DS error 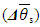 , the mathematical apparatus of differential calculus was applied [12]:
, the mathematical apparatus of differential calculus was applied [12]: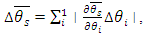
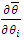 – partial derivatives of the function
– partial derivatives of the function 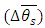 with respect to one of the several variables
with respect to one of the several variables 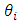 that affect
that affect 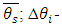 the uncertainty or error.For the present example, according to Equation (9), one can find an absolute total DS error of the indirect measurement
the uncertainty or error.For the present example, according to Equation (9), one can find an absolute total DS error of the indirect measurement 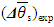 , reached in the experiment:
, reached in the experiment: 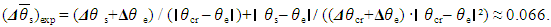
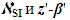 , one gets a DS error value
, one gets a DS error value 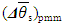 for the chosen PMM:
for the chosen PMM: 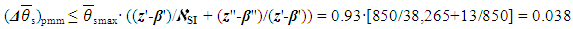
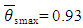 is a given range of changes of the DS final temperature [9] allowed by the chosen PMM. From (10) and (11), we get
is a given range of changes of the DS final temperature [9] allowed by the chosen PMM. From (10) and (11), we get 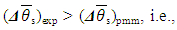 an actual error in the experiment is 1.7 times (0.066/0.038) more than the possible minimum. It means, at the chosen number of DS criteria the existing accuracy of DL variable’s measurement is not enough. In addition, the number of the recorded DS variables z*-β*=13 is less than the recommended ≈19 that corresponds to the lowest comparative error. For further experimental work it is required to use devices of a higher class of accuracy sufficient to confirm/clarify a new PMM designed with lots of DS variables.In this example there is introduced a full explanation of the required steps in order to analyze experimental data and to compare it with results obtained by computer realization of PMM.
an actual error in the experiment is 1.7 times (0.066/0.038) more than the possible minimum. It means, at the chosen number of DS criteria the existing accuracy of DL variable’s measurement is not enough. In addition, the number of the recorded DS variables z*-β*=13 is less than the recommended ≈19 that corresponds to the lowest comparative error. For further experimental work it is required to use devices of a higher class of accuracy sufficient to confirm/clarify a new PMM designed with lots of DS variables.In this example there is introduced a full explanation of the required steps in order to analyze experimental data and to compare it with results obtained by computer realization of PMM. 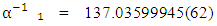 with a relative uncertainty r₁ of
with a relative uncertainty r₁ of 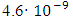 . It means that absolute uncertainty is
. It means that absolute uncertainty is 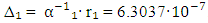 . The declared range S₁ of
. The declared range S₁ of 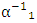 variations is
variations is 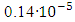 (see Fig. 4, [13]). Research is organized into the frame of COPSI ≡ LMТ. One can calculate the achieved comparative error
(see Fig. 4, [13]). Research is organized into the frame of COPSI ≡ LMТ. One can calculate the achieved comparative error 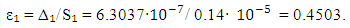
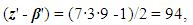
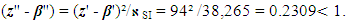
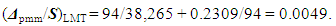
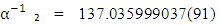 with a relative uncertainty
with a relative uncertainty 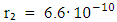 [14]. It means that absolute uncertainty is
[14]. It means that absolute uncertainty is 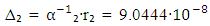 . Following the description of the experimental unit and methods, COPSI ≡ LMТ. According to Equation (15), the lowest comparative error equals 0.0049. The range of variations S₂ of
. Following the description of the experimental unit and methods, COPSI ≡ LMТ. According to Equation (15), the lowest comparative error equals 0.0049. The range of variations S₂ of 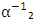 is
is 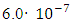 (see Fig.1, [14]). In this case, the comparative error of the experimental method will be
(see Fig.1, [14]). In this case, the comparative error of the experimental method will be 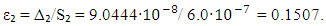
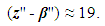
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML