-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2015; 5(5): 154-158
doi:10.5923/j.ajcam.20150505.04
Assessment of Human Skills Using Trapezoidal Fuzzy Numbers (Part II)
Michael Gr. Voskoglou
Department of Mathematical Sciences, School of Technological Applications, Graduate Technological Educational Institute (T. E. I.) of Western Greece, Patras, Greece
Correspondence to: Michael Gr. Voskoglou, Department of Mathematical Sciences, School of Technological Applications, Graduate Technological Educational Institute (T. E. I.) of Western Greece, Patras, Greece.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In an earlier work, recently published in this journal, we have used the Trapezoidal Fuzzy Numbers (TpFNs) as an assessment tool of human skills. This approach led to an approximate linguistic characterization of the corresponding group’s overall performance, but it was not proved to be always sufficient for comparing the performance of two different human groups, since two TpFNs are not always comparable. In this paper we complete the above fuzzy assessment approach by presenting a defuzzification method of TpFNS based on the Center of Gravity (COG) technique, which enables the required comparison of the performance of two (or more) groups.
Keywords: Human Assessment, Fuzzy Logic, Fuzzy Numbers (FNs), Triangular (TFNs) and Trapezoidal (TpFNs) Fuzzy Numbers, Center of Gravity (COG) Defuzzification Technique
Cite this paper: Michael Gr. Voskoglou, Assessment of Human Skills Using Trapezoidal Fuzzy Numbers (Part II), American Journal of Computational and Applied Mathematics , Vol. 5 No. 5, 2015, pp. 154-158. doi: 10.5923/j.ajcam.20150505.04.
Article Outline
1. Introduction
- The social demand of classifying humans according to their qualifications makes the assessment of human skills a very important task. Fuzzy logic, due to its nature of characterizing an ambiguous case with multiple values, offers rich resources for the assessment purposes. This gave us several times in past the impulse to apply principles of fuzzy logic for assessing human skills using as tools the corresponding system’s uncertainty (e.g. see [8] and its relevant references, Section 3 of [9], etc), the COG defuzzification technique (e.g. see [5], Section 3 of [9], etc), as well as two recently developed variations of the COG technique, i.e. the Triangular (TFAM) and Trapezoidal (TpFAM) Fuzzy Assessment Models (e.g. see [6] and [11] respectively, etc). It is of worth to notice that the TFAM and TpFAM, which are equivalent to each other since they obtain exactly the same results, treat better than the COG technique the ambiguous assessment cases being at the boundaries between two successive assessment grades. The use of the COG technique for assessment purposes, as well as the above mentioned two variations of it were initiated by Igor Subbotin, Professor of Mathematics at State University in Los Angeles and Voskoglou’s coauthor in many publications (e.g. [6], [11], etc). In a recently published paper [12] we have extend our above researches by using the Trapezoidal Fuzzy Numbers (TpFNs) as an assessment tool of human skills. This approach, while it is better than our older fuzzy methods for the individual assessment [10], in case of group assessment led (in [12]) to an approximate characterization of the group’s overall performance and it was not proved to be always sufficient for comparing the performance of two different groups (for more details see below Example 1 of Section 4). In this paper we complete the above fuzzy assessment approach by presenting a defuzzification method of TpFNS based on the Center of Gravity (COG) technique, which enables the required comparison of the performance of two (or more) groups. The rest of the paper is organized as follows: In Section 2 we recall in brief some definitions presented in [12], which are necessary for the understanding of the present paper. In Section 3 we present the defuzzification method for TpFNs based on the COG technique. In Section 4 we reconsider and we extend an example originally presented in [12] and we apply our defuzzification method on the outputs (TpFNs) of the extended example for comparing the performance of two basket-ball teams. Finally, Section 5 is devoted to our conclusion and a brief discussion on the perspectives of future research on the subject.
2. Introductory Definitions
- In this Section we recall in brief some definitions presented in [12], which are necessary for the understanding of the present paper. For general facts on fuzzy sets we refer to the book of Klir and Folger [4].We start with the definition of a fuzzy number:Definition 1: A Fuzzy Number is a normal (i.e. there exists x in R, such that m(x) = 1) and convex (i.e. its x-cuts1 Ax are ordinary closed real intervals, for all x in [0, 1]) fuzzy set A on the set R of real numbers with a piecewise continuous membership function y = m(x).The following statement defines a partial order on the set of all FNs:Definition 2: Given the FNs A and B we write A≤B (or
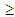 ) if, and only if,
) if, and only if, 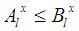 and
and 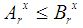 (or
(or ) for all x in [0, 1]. Two FNs for which the above relation holds are called comparable, otherwise they are called non comparable.FNs play a fundamental role in fuzzy mathematics, analogous to the role played by the ordinary numbers in classical mathematics. For general facts on FNs we refer to Chapter 3 of the book [7], which is written in Greek language, and also to the classical on the subject book [3].
) for all x in [0, 1]. Two FNs for which the above relation holds are called comparable, otherwise they are called non comparable.FNs play a fundamental role in fuzzy mathematics, analogous to the role played by the ordinary numbers in classical mathematics. For general facts on FNs we refer to Chapter 3 of the book [7], which is written in Greek language, and also to the classical on the subject book [3].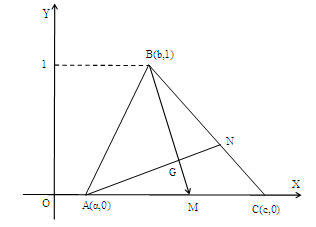 | Figure 1. Graph and COG of the TFN (a, b, c) |
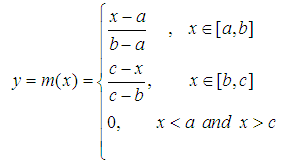 Obviously we have that m(b)=1, while b need not be in the “middle” of a and c.
Obviously we have that m(b)=1, while b need not be in the “middle” of a and c.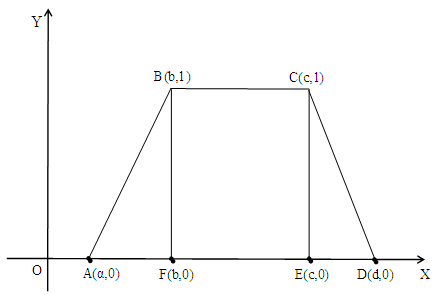 | Figure 2. Graph of the TpFN (a, b, c, d) |
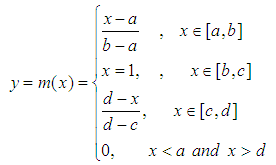 Obviously the TpFNs are generalizations of TFNs. In fact, the TFN (a, b, d) can be considered as a special case of the TpFN (a, b, c, d) with b=c.It can be shown that the two well known general methods for performing operations between FNs (e.g. see Section 3 of [12]) lead to the following simple rules for the addition and subtraction of TpFNs:Definition 5: Let A = (a1, a2, a3, a4) and B = (b1, b2, b3, b4) be two TFNs. Then● The sum A + B = (a1+b1, a2+b2, a3+b3, a4+b4).● The difference A - B = A + (-B) = (a1-b4, a2-b3, a3-b2, a4-b1), where –B = (-b4, -b3, -b2, -b1) is defined to be the opposite of B.In other words, the opposite of a TpFN, as well as the sum and the difference of two TpFNs are also TpFNs. On the contrary, the product and the quotient of two TFNs, although they are FNs, they are not always TpFNs, apart from some special cases, or in terms of suitable approximating formulas (for more details see [2]).Definition 6: We define the following two scalar operations:● k + A= (k+a1, k+a2, k+a3, k+a4), k
Obviously the TpFNs are generalizations of TFNs. In fact, the TFN (a, b, d) can be considered as a special case of the TpFN (a, b, c, d) with b=c.It can be shown that the two well known general methods for performing operations between FNs (e.g. see Section 3 of [12]) lead to the following simple rules for the addition and subtraction of TpFNs:Definition 5: Let A = (a1, a2, a3, a4) and B = (b1, b2, b3, b4) be two TFNs. Then● The sum A + B = (a1+b1, a2+b2, a3+b3, a4+b4).● The difference A - B = A + (-B) = (a1-b4, a2-b3, a3-b2, a4-b1), where –B = (-b4, -b3, -b2, -b1) is defined to be the opposite of B.In other words, the opposite of a TpFN, as well as the sum and the difference of two TpFNs are also TpFNs. On the contrary, the product and the quotient of two TFNs, although they are FNs, they are not always TpFNs, apart from some special cases, or in terms of suitable approximating formulas (for more details see [2]).Definition 6: We define the following two scalar operations:● k + A= (k+a1, k+a2, k+a3, k+a4), k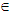 R● kA = (ka1, ka2, ka3, ka4), if k>0 and kA = (ka4, ka3, ka2, ka1), if k<0.We close this section with the following definition, which will be used Section 4 for assessing the overall performance of a human group with the help of TpFNs:Definition 7: Let Ai = (a1i, a2i, a3i, a4i), i = 1, 2,…, n be TpFNs, where n is a non negative integer, n
R● kA = (ka1, ka2, ka3, ka4), if k>0 and kA = (ka4, ka3, ka2, ka1), if k<0.We close this section with the following definition, which will be used Section 4 for assessing the overall performance of a human group with the help of TpFNs:Definition 7: Let Ai = (a1i, a2i, a3i, a4i), i = 1, 2,…, n be TpFNs, where n is a non negative integer, n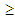 2. Then we define the mean value of the above TpFNs to be the TpFN: A =
2. Then we define the mean value of the above TpFNs to be the TpFN: A = 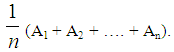
3. Defuzzification of TFNs/TpFNs
- In this section we shall use the COG technique for defuzzifying a given TFN/TpFN. We start with the case of TFNs:Proposition 1: The coordinates (X, Y) of the COG of the graph of the TFN (a, b, c) are calculated by the formulas X =
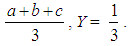 Proof: The graph of the TFN (a, b, c) is the triangle ABC of Figure 1, where A (a, 0), B (b, 1) and C (c, 0). Then, the COG, say G, of ABC is the intersection point of its medians AN and BM, where N
Proof: The graph of the TFN (a, b, c) is the triangle ABC of Figure 1, where A (a, 0), B (b, 1) and C (c, 0). Then, the COG, say G, of ABC is the intersection point of its medians AN and BM, where N 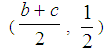 and
and 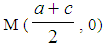 . Therefore the equation of the straight line on which AN lies is
. Therefore the equation of the straight line on which AN lies is 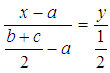 , or
, or 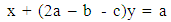 | (1) |
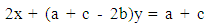 | (2) |
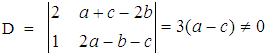 , the linear system of (1) and (2) has a unique solution with the respect to the variables x and y determining the coordinates of the triangle’s COG.The proof of the Proposition is completed by observing that
, the linear system of (1) and (2) has a unique solution with the respect to the variables x and y determining the coordinates of the triangle’s COG.The proof of the Proposition is completed by observing that 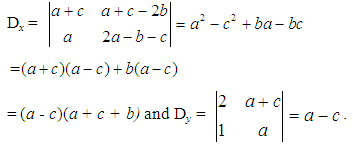 Next, Proposition 1 will be used as a Lemma for the defuzzification of TpFNs. The corresponding result is the following:Proposition 2: The coordinates (X, Y) of the COG of the graph of the TpFN (a, b, c, d) are calculated by the formulas
Next, Proposition 1 will be used as a Lemma for the defuzzification of TpFNs. The corresponding result is the following:Proposition 2: The coordinates (X, Y) of the COG of the graph of the TpFN (a, b, c, d) are calculated by the formulas 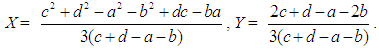 Proof: We divide the trapezoid forming the graph of the TpFN (a, b, c, d) in three parts, two triangles and one rectangle (Figure 2). The coordinates of the three vertices of the triangle ABE are (a, 0), (b, 1) and (b, 0) respectively, therefore by Proposition 1 the COG of this triangle is the point
Proof: We divide the trapezoid forming the graph of the TpFN (a, b, c, d) in three parts, two triangles and one rectangle (Figure 2). The coordinates of the three vertices of the triangle ABE are (a, 0), (b, 1) and (b, 0) respectively, therefore by Proposition 1 the COG of this triangle is the point 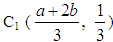 . Similarly one finds that the COG of the triangle FCD is the point
. Similarly one finds that the COG of the triangle FCD is the point 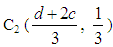 . Also, it is easy to check that the COG of the rectangle BCFE is the point C3
. Also, it is easy to check that the COG of the rectangle BCFE is the point C3 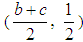 . Further, the areas of the two triangles are equal to
. Further, the areas of the two triangles are equal to 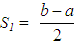 and S2 =
and S2 = 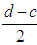 respectively, while the area of the rectangle is equal to S3 = c- b. It is well known then (e.g. see [35]) that the coordinates of the COG of the trapezoid, being the resultant of the COGs Ci (xi, yi), for i=1, 2, 3, are calculated by the formulas X =
respectively, while the area of the rectangle is equal to S3 = c- b. It is well known then (e.g. see [35]) that the coordinates of the COG of the trapezoid, being the resultant of the COGs Ci (xi, yi), for i=1, 2, 3, are calculated by the formulas X = 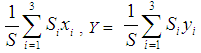 (3), where S = S1 + S2 + S3 =
(3), where S = S1 + S2 + S3 = 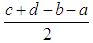 is the area of the trapezoid.The proof of the Proposition is completed by replacing the above found values of S, Si, xi and yi, i = 1, 2, 3, in formulas (3) and by performing the corresponding operations.
is the area of the trapezoid.The proof of the Proposition is completed by replacing the above found values of S, Si, xi and yi, i = 1, 2, 3, in formulas (3) and by performing the corresponding operations.4. Use of the TpFNs for Assessing Human Skills
- We reconsider first the following example originally presented in [12]:Example 1: The performance of the five players of a basket-ball team who started a game was individually assessed by six different athletic journalists using a scale from 0 to 100 as follows: P1 (player 1): 43, 48, 49, 49, 50, 52, P2: 81, 83. 85, 88, 91, 95, P3: 76, 82, 89, 95, 95, 98, P4: 86, 86, 87, 87, 87, 88 and P5: 35, 40, 44, 52, 59, 62.The players’ performance is characterized by the fuzzy linguistic labels (grades) A, B, C, D and F corresponding to the above scores as follows: A (85-100) = excellent, B (84-75) = very good, C (74-60) = good, D (59-50) = fair and F (<50) = unsatisfactory. How one can assess their individual and overall performances in this game? For this, in [12] we have assigned to each basket-ball player Pi a TpFN (denoted, for simplicity, by the same letter) as follows: P1 = (0, 43, 52, 59), P2 = (75, 81, 95, 100), P3 = (75, 76, 98, 100), P4 = (85, 86, 88, 100) and P5 = (0, 35, 62, 74). Each of the above TpFNs characterizes the individual performance of the corresponding player in the form (a, b, c, d), where a and d are the lower and upper bounds respectively of his performance with respect to the scores assigned to the linguistic grades A, B, C, D and F, while b and c are the lower and higher scores respectively assigned to the corresponding player by the athletic journalists. Further, for assessing the overall performance of the above five players, we have calculated in [12] the mean value of the TpFNs Pi , i =1, 2, 3, 4, 5 (see Definition 7), which is equal to
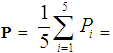 (47, 64.2, 79, 86.6). The value of P gives the information that the five players’ performance fluctuates from unsatisfactory (a = 47) to excellent (d = 86.6), while their overall performance lies in the interval [b, c] = [64.2, 79], i.e. it can be characterized from good (C) to very good (B). Further, in [12] we have noticed that this approach is not always appropriate to be used alone when one wants to compare the overall performance of two or more groups of players, because two (or more) TpFNs are not always comparable (see Definition 2). However, under the light of Proposition 2, we are now in position to overcome this difficulty by defuzzifying the corresponding TpFNs. In order to illustrate this in practice we extend Example 1 as follows:Example 2: Reconsider Example 1 and assume that the same six journalits assessed also the performance of the five players of the opponent team who started the same basket-ball game. Assume further that the overall performance of the first five players of the second team was assessed as in Example 1 using TpFNs and that the mean value of the corresponding TpFNs was found to be equal to P΄ = (47.8, 65.3, 78.1, 85.9). How one can compare the overall performance of the two teams?For this, applying Proposition 2 one finds that the x-coordinate of the COC of the trapezoid constituting the graph of the TpFN P is equal to
(47, 64.2, 79, 86.6). The value of P gives the information that the five players’ performance fluctuates from unsatisfactory (a = 47) to excellent (d = 86.6), while their overall performance lies in the interval [b, c] = [64.2, 79], i.e. it can be characterized from good (C) to very good (B). Further, in [12] we have noticed that this approach is not always appropriate to be used alone when one wants to compare the overall performance of two or more groups of players, because two (or more) TpFNs are not always comparable (see Definition 2). However, under the light of Proposition 2, we are now in position to overcome this difficulty by defuzzifying the corresponding TpFNs. In order to illustrate this in practice we extend Example 1 as follows:Example 2: Reconsider Example 1 and assume that the same six journalits assessed also the performance of the five players of the opponent team who started the same basket-ball game. Assume further that the overall performance of the first five players of the second team was assessed as in Example 1 using TpFNs and that the mean value of the corresponding TpFNs was found to be equal to P΄ = (47.8, 65.3, 78.1, 85.9). How one can compare the overall performance of the two teams?For this, applying Proposition 2 one finds that the x-coordinate of the COC of the trapezoid constituting the graph of the TpFN P is equal to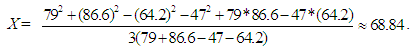 In the same way one finds that the x-coordinate X ‘of the graph of P΄ is approximately equal to 68.13. Observe now that the GOGs of the graphs of P and P΄ lie in a rectangle with sides of length 100 units on the X-axis (player scores from 0 to 100) and one unit on the Y-axis (normal fuzzy sets). Therefore, the nearer the x-coordinate of the COG to 100, the better the corresponding team’s performance, Thus, since X > X’, the first team demonstrates a better overall performance than the second one.Remark: In the same way as in Example 2 one can defuzzify the TpFNs Pi, i=1, 2, 3, 4, 5 of Example 1 corresponding to the five players of the first basket-ball team. In this way it becomes possible to compare the individual performance of any two players, in contrast to our method presented in [10] and the equivalent to it method of A. Jones [1] that define a partial order only on the individual performances.
In the same way one finds that the x-coordinate X ‘of the graph of P΄ is approximately equal to 68.13. Observe now that the GOGs of the graphs of P and P΄ lie in a rectangle with sides of length 100 units on the X-axis (player scores from 0 to 100) and one unit on the Y-axis (normal fuzzy sets). Therefore, the nearer the x-coordinate of the COG to 100, the better the corresponding team’s performance, Thus, since X > X’, the first team demonstrates a better overall performance than the second one.Remark: In the same way as in Example 2 one can defuzzify the TpFNs Pi, i=1, 2, 3, 4, 5 of Example 1 corresponding to the five players of the first basket-ball team. In this way it becomes possible to compare the individual performance of any two players, in contrast to our method presented in [10] and the equivalent to it method of A. Jones [1] that define a partial order only on the individual performances.5. Conclusions
- In the present paper we used the TpFNs as a tool for assessing human skills. The main advantage of this approach is that in case of individual assessment it is sufficient for comparing the performances of all students, in contrast to the alternative fuzzy assessment methods applied in earlier works, which define a partial order only on the individual performances. However, in case of group assessment the TpFNs approach initially leads to an approximate characterization of the group’s overall performance, which is not always sufficient for comparing the performances of two different groups, as our fuzzy assessment methods applied in earlier works do. This is due to the fact that the inequality between TpFNs defines on them a relation of partial order only. Therefore, in cases where our fuzzy outputs are not comparable, some extra calculations are needed in order to obtain the required comparison by defuzzifying these outputs. This could be considered as a disadvantage of this approach, although the extra calculations needed are very simple.Further, our new method of using TpFNs for the assessment of human skills is of general character, which means that it could be utilized for assessing a great variety of human (or machine; e.g. CBR systems [11]) activities. This is one of the main targets of our future research on the subject.
ACKNOWLEDGEMENTS
- The author wishes to thank his colleagues Prof. J. Theodorou, Graduate Technological Educational Institute of Central Greece and Prof. I. Subbotin, State University, Los Angeles, for their helpful ideas about FNs.
Note
- 1. Let x be a real number of the interval [0, 1]. We recall then that the x-cut of a fuzzy set A on U, denoted by Ax, is defined to be the crisp set Ax = {y
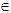 U: m(y)
U: m(y) 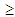 x}.
x}. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML