Olabode B. T., Omole Ezekiel O.
Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria
Correspondence to: Olabode B. T., Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This article proposes a new class of Implicit Hybrid Block Numerov- type methods for the direct solution of fourth order initial value problems of ordinary differential equations. This was achieved by constructing a continuous representation of Implicit hybrid Numerov-type schemes via interpolation and collocation of the approximate and derivative function respectively. The main discrete scheme was generated and new additional schemes were evaluated, which are combined and applied in block form as simultaneous numerical integrators. Of great interest are the basic properties of the new method such as, convergence, order, error constant and zero-stability. These basic properties were investigated. The performances of the methods were demonstrated on some numerical examples to show accuracy and efficiency advantages. The results compare favourably with the results when the same schemes are implemented in predictor-corrector mode.
Keywords:
Numerov-type methods,Implicit Hybrid Scheme, Ordinary Differential Equations (ODEs), Initial Value Problems (IVPs)
Cite this paper: Olabode B. T., Omole Ezekiel O., Implicit Hybrid Block Numerov-Type Method for the Direct Solution of Fourth-Order Ordinary Differential Equations, American Journal of Computational and Applied Mathematics , Vol. 5 No. 5, 2015, pp. 129-139. doi: 10.5923/j.ajcam.20150505.01.
1. Introduction
Consider the nth-order initial value problem of ordinary differential equation of the form;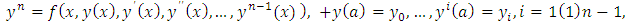 | (1) |
where 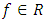 is sufficiently differentiable and satisfies a Lipschitz condition. This class of problems has a wide variety of applications in science and engineering field especially in mechanical systems without dissipation, control theory and celestial mechanics (see Laudau and Liftshitz (1989); Liboff (1980)). However, only a limited number of analytical methods are available for solving (1) directly without reducing it to a first order system of differential equations. There exists an extensive literature on numerical methods for the solution of ordinary differential equations (see, for example Lambert (1973, 1976, 1991), Adee et al., (2005), Awoyemi and Idowu (2005), Twizell and Khaliq (1984) and Sirisena et al., (2004)). In particular, Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third–order ordinary differential equations. Sirisena et al., (2004)) constructed a Butcher- type two-step hybrid multistep method for accurate and efficient parallel solution of ordinary differential equations.Hybrid methods were first proposed to overcome the Dahlquist (1956) barrier theorem whereby the conventional linear multistep method was modified to incorporating off-step points of derivation process (see Lambert (1973) and Gear (1965)). They utilize data at other points, other than the step points
is sufficiently differentiable and satisfies a Lipschitz condition. This class of problems has a wide variety of applications in science and engineering field especially in mechanical systems without dissipation, control theory and celestial mechanics (see Laudau and Liftshitz (1989); Liboff (1980)). However, only a limited number of analytical methods are available for solving (1) directly without reducing it to a first order system of differential equations. There exists an extensive literature on numerical methods for the solution of ordinary differential equations (see, for example Lambert (1973, 1976, 1991), Adee et al., (2005), Awoyemi and Idowu (2005), Twizell and Khaliq (1984) and Sirisena et al., (2004)). In particular, Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third–order ordinary differential equations. Sirisena et al., (2004)) constructed a Butcher- type two-step hybrid multistep method for accurate and efficient parallel solution of ordinary differential equations.Hybrid methods were first proposed to overcome the Dahlquist (1956) barrier theorem whereby the conventional linear multistep method was modified to incorporating off-step points of derivation process (see Lambert (1973) and Gear (1965)). They utilize data at other points, other than the step points 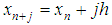 . Hybrid methods increase the order of the method while preserving good stability properties. Thompson and Gonzalez (1997) described Numerov’s method as an efficient and one of the most widely used algorithms for solving special second order linear ordinary differential equations of the form
. Hybrid methods increase the order of the method while preserving good stability properties. Thompson and Gonzalez (1997) described Numerov’s method as an efficient and one of the most widely used algorithms for solving special second order linear ordinary differential equations of the form 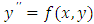 . He gave the following examples; one-dimensional time- independent
. He gave the following examples; one-dimensional time- independent 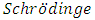 equation, the equation of motion of an undamped forced harmonic oscillator and Poisson’s equations.Moreover, according to Vigo-Aguiar and Ramos (2005), different authors have dealt with
equation, the equation of motion of an undamped forced harmonic oscillator and Poisson’s equations.Moreover, according to Vigo-Aguiar and Ramos (2005), different authors have dealt with 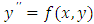 in providing different approaches to solving it, but the pioneer work was probably due to
in providing different approaches to solving it, but the pioneer work was probably due to 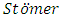 (Lambert (1973)), who developed his method in connection with numerical calculations concerning the aurora borealis. The k-step
(Lambert (1973)), who developed his method in connection with numerical calculations concerning the aurora borealis. The k-step 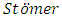 method may be derived similarly to the Adams method, by twice integrating the differential equation and then replacing f by the interpolating polynomial passing through the points
method may be derived similarly to the Adams method, by twice integrating the differential equation and then replacing f by the interpolating polynomial passing through the points 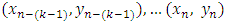 , where the
, where the 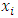 are equally spaced. However, to obtain more accurate formulas, it is possible used the interpolation polynomial passing through the additional points
are equally spaced. However, to obtain more accurate formulas, it is possible used the interpolation polynomial passing through the additional points 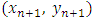 in which implicit
in which implicit 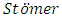 method was obtained (also known in certain contexts as the Cowell method or the Numerov method) (Vigo-Aguiar and Ramos (2005)). In Hans Van de Vyver (2007), an explicit Numerov-type method for second-order differential equations with oscillating solution was proposed. All authors mentioned above independently developed Numerov’s methods for the solution of special second order ordinary differential equations but little discussion was devoted to the modification of Numerov’s method to handle general higher order ordinary differential equations.In the research work of Awari et al., (2013), the application of two-step continuous hybrid Butcher’s method in block form for the solution of first order initial value problem was considered. Akinfenwa et al., (2011) derived implicit two step continuous hybrid block methods with four off-steps points for solving stiff ordinary differential equation. Therefore, this article proposes a class of continuous implicit hybrid block Numerov- type method for the direct solution of fourth order ordinary differential equations directly without reducing to system of first-order ordinary differential equations. The block methods can be seen as a set of linear multistep methods simultaneously applied to (1) and then combined to yield an approximation with better accuracy, better stability, better efficiency in parallel computing. λDefinition 1.1: The block method is said to be zero-stable if the roots
method was obtained (also known in certain contexts as the Cowell method or the Numerov method) (Vigo-Aguiar and Ramos (2005)). In Hans Van de Vyver (2007), an explicit Numerov-type method for second-order differential equations with oscillating solution was proposed. All authors mentioned above independently developed Numerov’s methods for the solution of special second order ordinary differential equations but little discussion was devoted to the modification of Numerov’s method to handle general higher order ordinary differential equations.In the research work of Awari et al., (2013), the application of two-step continuous hybrid Butcher’s method in block form for the solution of first order initial value problem was considered. Akinfenwa et al., (2011) derived implicit two step continuous hybrid block methods with four off-steps points for solving stiff ordinary differential equation. Therefore, this article proposes a class of continuous implicit hybrid block Numerov- type method for the direct solution of fourth order ordinary differential equations directly without reducing to system of first-order ordinary differential equations. The block methods can be seen as a set of linear multistep methods simultaneously applied to (1) and then combined to yield an approximation with better accuracy, better stability, better efficiency in parallel computing. λDefinition 1.1: The block method is said to be zero-stable if the roots 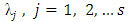 of the characteristic polynomial
of the characteristic polynomial 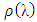 defined by
defined by 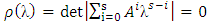 satisfies
satisfies 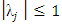 and for those roots with
and for those roots with 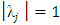 , the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals
, the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals 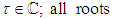
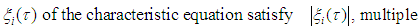
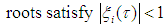 is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition 1.3: The LMM is said to be consistent if it has order
is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition 1.3: The LMM is said to be consistent if it has order 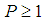 .The paper is organized as follows. Section 1 is of an introductory nature. The construction and implementation of the implicit hybrid block Numerov -type methods were described in Section 2. Stability analysis of the new methods was discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.
.The paper is organized as follows. Section 1 is of an introductory nature. The construction and implementation of the implicit hybrid block Numerov -type methods were described in Section 2. Stability analysis of the new methods was discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.
2. Construction of the Implicit Hybrid Block Numerov-Type Methods
Consider the fourth-order initial value problem: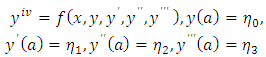 | (2) |
where f is sufficiently smooth, 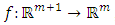 , y is an m-dimensional vector and
, y is an m-dimensional vector and  is a scalar variable and a set of equally spaced points on the integration interval also given by
is a scalar variable and a set of equally spaced points on the integration interval also given by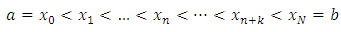 with a specified positive integer step number k greater than zero. In this work, h is assumed to be a constant step-size given by
with a specified positive integer step number k greater than zero. In this work, h is assumed to be a constant step-size given by 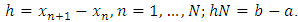 Assuming an approximate solution to (2) in form
Assuming an approximate solution to (2) in form 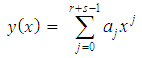 | (3) |
where 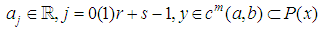 , r is the interpolation points and s is the collocation points. The highest derivative of (3) is given as:
, r is the interpolation points and s is the collocation points. The highest derivative of (3) is given as: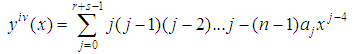 | (4) |
From (2) and (4), one obtains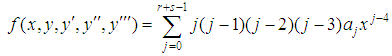 | (5) |
For one-step method 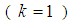 , we collocate (5) at
, we collocate (5) at 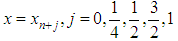 and interpolate (3) at
and interpolate (3) at 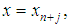
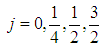 lead to system of equations with parameters
lead to system of equations with parameters 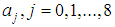 . Solving for these parameters and substituting into (3) using Maple software package, yields a linear multistep method with continuous coefficients of the form:
. Solving for these parameters and substituting into (3) using Maple software package, yields a linear multistep method with continuous coefficients of the form: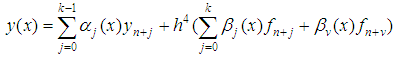 | (6) |
Using the transformation 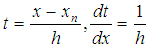 . The coefficients of
. The coefficients of 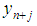 and
and 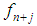 are obtained as:
are obtained as: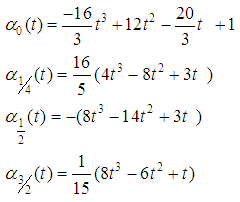
 | (7) |
Evaluating (6) at 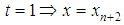 gives the discrete scheme:
gives the discrete scheme: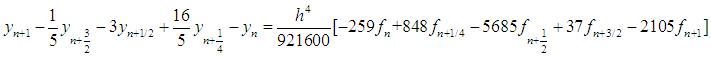 | (8) |
The discrete scheme (8) is consistent and of order 5 with error constant 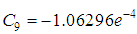 . The first, second and third derivatives of the continuous scheme (7) are found and evaluated at
. The first, second and third derivatives of the continuous scheme (7) are found and evaluated at 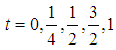 .Express explicitly as:
.Express explicitly as: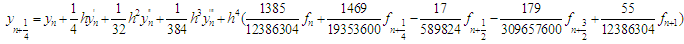 | (9) |
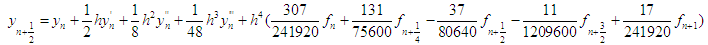 | (10) |
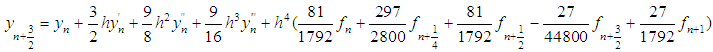 | (11) |
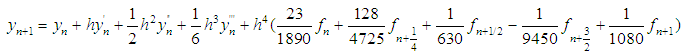 | (12) |
The implementation of this work was done in block mode in which the main method is constructed and additional schemes were evaluated, which are combined as a block and applied simultaneously process to solve (2). However, following Fatunla (1991, 1994), the general discrete block formula is given as: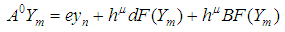 | (13) |
where e, d are vectors, B are RxR matrix and 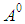 identity matrix, µ is the order of differential equation and
identity matrix, µ is the order of differential equation and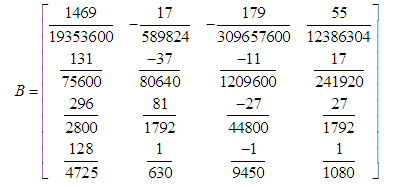 | (14) |
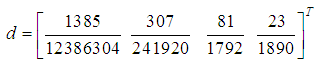 | (15) |
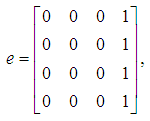 | (16) |
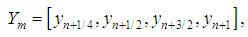 | (17) |
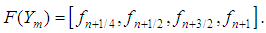 | (18) |
They are uniformly of order [5, 5, 5, 5]T with error constant 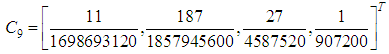 | (19) |
Comment: It is worth mentioning that all the discrete schemes arising from a single continuous formula and its derivatives functions when evaluate at 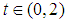 are independent and infinite are of uniform order of accuracy.Similarly, for two-step method (
are independent and infinite are of uniform order of accuracy.Similarly, for two-step method (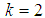 ), equation (5) is collocated at
), equation (5) is collocated at 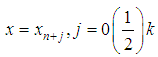 and equation (3) is interpolated at
and equation (3) is interpolated at 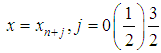 leads to a system of equations which after some manipulations yields the continuous method expressed in the form:
leads to a system of equations which after some manipulations yields the continuous method expressed in the form: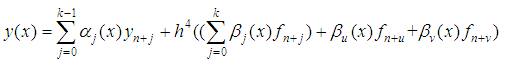 | (20) |
where 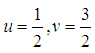 .The coefficients
.The coefficients 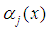 and
and 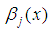 are expressed as functions of t .
are expressed as functions of t .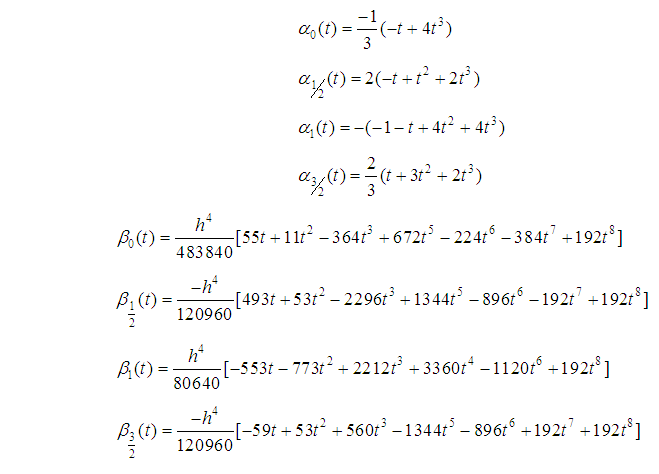
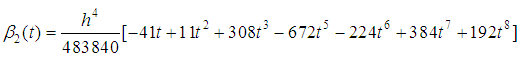 | (21) |
Evaluating (21) at 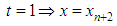 gives the discrete scheme
gives the discrete scheme 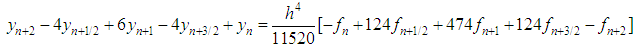 | (22) |
The discrete scheme (22) is consistent and of order 6 with error constant 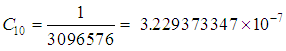 . The first, second and third derivatives of the continuous scheme (21) are found and evaluated at
. The first, second and third derivatives of the continuous scheme (21) are found and evaluated at 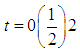 and after some manipulations gives the explicit discrete block schemes:
and after some manipulations gives the explicit discrete block schemes: 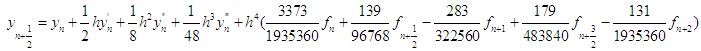 | (23) |
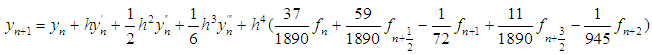 | (24) |
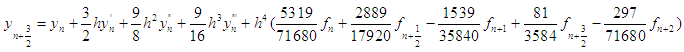 | (25) |
 | (26) |
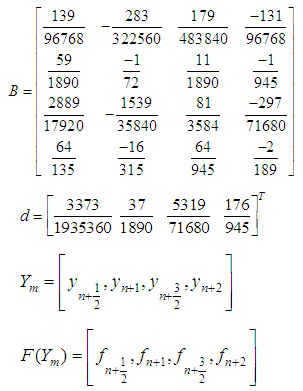 | (27) |
The block discrete schemes are uniformly of order six that is [6,6,6,6]T with error constant 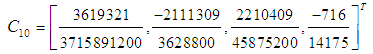 | (31) |
In the case three-step method 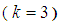 , collocation is done at
, collocation is done at 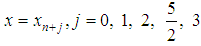 and interpolation is done at
and interpolation is done at 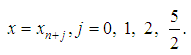 The continuous linear multistep method is given in the form:
The continuous linear multistep method is given in the form: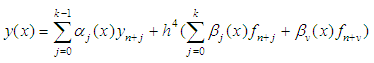 | (32) |
where 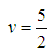 and the coefficients
and the coefficients 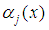 and
and 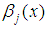 are expressed as.
are expressed as. 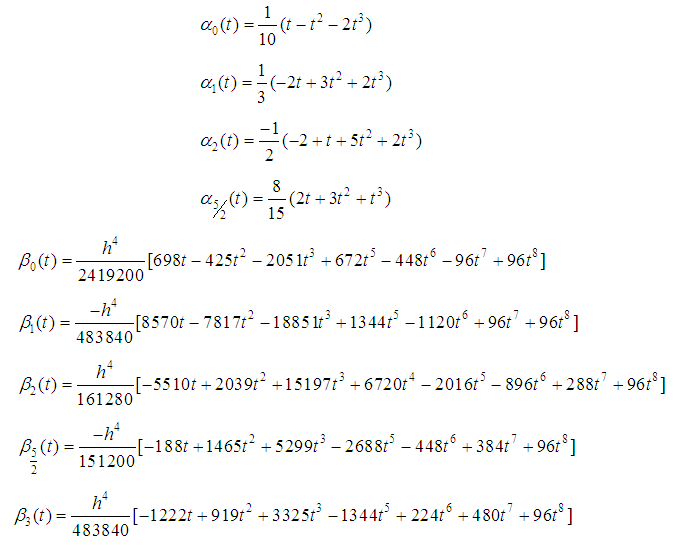 | (33) |
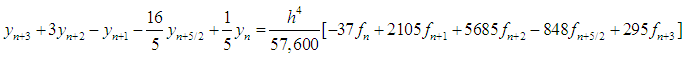 | (34) |
The discrete scheme is of order 7 with error constant 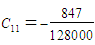 . The main discrete scheme and the additional schemes obtained are writing explicitly as:
. The main discrete scheme and the additional schemes obtained are writing explicitly as: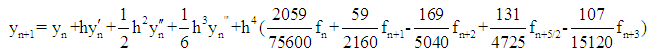 | (35) |
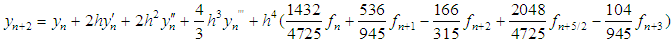 | (36) |
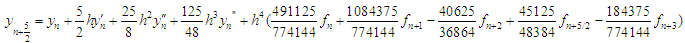 | (37) |
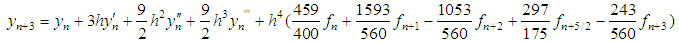 | (38) |
Express in block form of (13) where 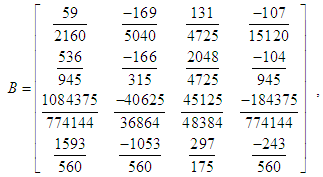 | (39) |
 | (40) |
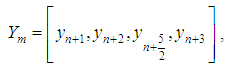 | (41) |
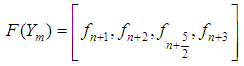 | (42) |
The explicit discrete schemes in block form are uniformly of order seven that is [7, 7, 7, 7]T with error constant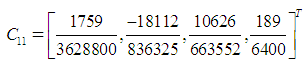 | (43) |
3. Stability Analysis
To investigate the stability properties of methods for solving the initial value problem (2), the block method (13) was normalized for easy analysis (see Fatunla (1994), Yusuph and Onumanyi (2002). The single block for the one-step method, two-step method and three-step method have the same first characteristic polynomial of the form:
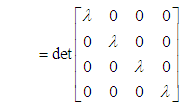
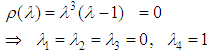 This satisfies the condition for method (13) to be zero –stable. Hence the block method is zero stable (see definition (1.1), (1.2) and (1.3). The block method is also consistent, as it has the order p greater than 1. Hence the convergence of the method is asserted as in the theorem 3.1 below.Theorem 3.1: (Dahlquist 1956)The necessary and sufficient conditions for a linear multistep to be convergent are that it be consistent and zero-stable.
This satisfies the condition for method (13) to be zero –stable. Hence the block method is zero stable (see definition (1.1), (1.2) and (1.3). The block method is also consistent, as it has the order p greater than 1. Hence the convergence of the method is asserted as in the theorem 3.1 below.Theorem 3.1: (Dahlquist 1956)The necessary and sufficient conditions for a linear multistep to be convergent are that it be consistent and zero-stable.
3.1. Region of Absolute Stability of the Method
The Locus method is used to determine the region of absolute stability (Lambert (1973)). The boundary locus method is given by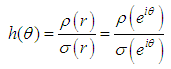 where
where 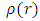 and
and 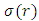 are the first and second characteristics polynomial respectively as:
are the first and second characteristics polynomial respectively as: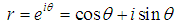 Using a Matlab program, the absolute stability region of the new methods is plotted below.
Using a Matlab program, the absolute stability region of the new methods is plotted below.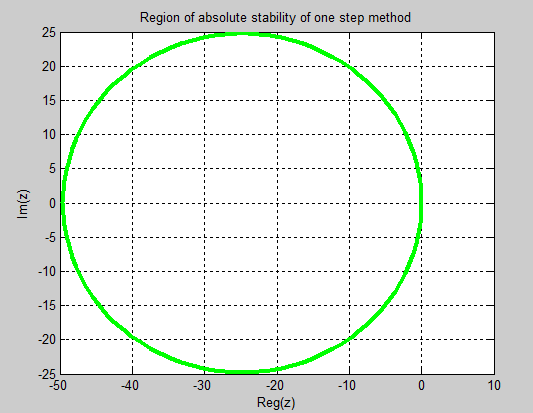 | Figure 1. Region of Absolute Stability (RAS) of Block of One-step Method |
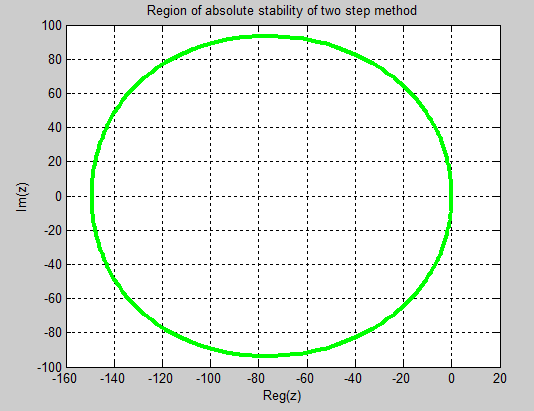 | Figure 2. Region of Absolute Stability (RAS) of Block of Two-step Method |
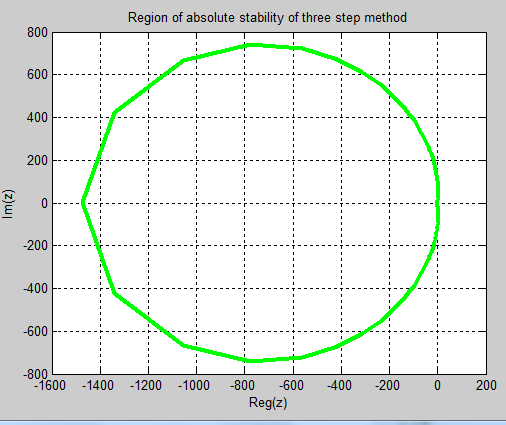 | Figure 3. Region of Absolute Stability (RAS) of the Block of Three–step Method |
4. Numerical Experiments and Results
This section deals with the numerical experiments and results. The derived schemes were tested on the following problems. Problem 1Consider the non- linear fourth order ordinary differential equation 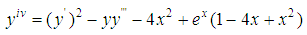 Subject to the initial condition
Subject to the initial condition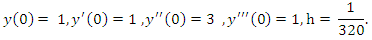 Problem 2
Problem 2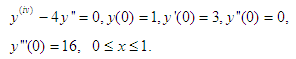 The theoretical solution is given as
The theoretical solution is given as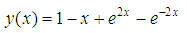 Problem 3
Problem 3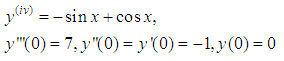 Exact Solution
Exact Solution 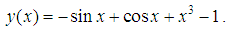 Problem 4Consider the non-homogeneous linear equation of fourth order below
Problem 4Consider the non-homogeneous linear equation of fourth order below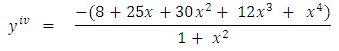 Subject to the initial conditions
Subject to the initial conditions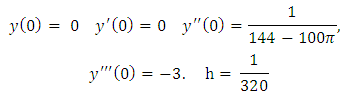 The theoretical solution is
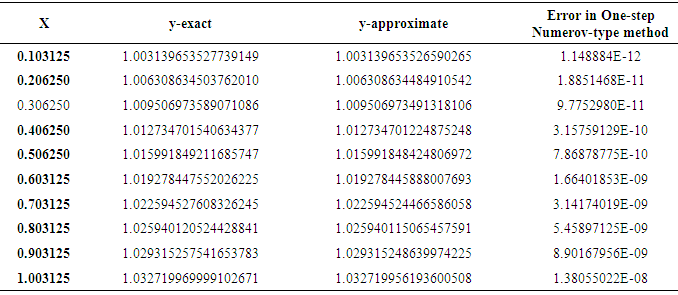
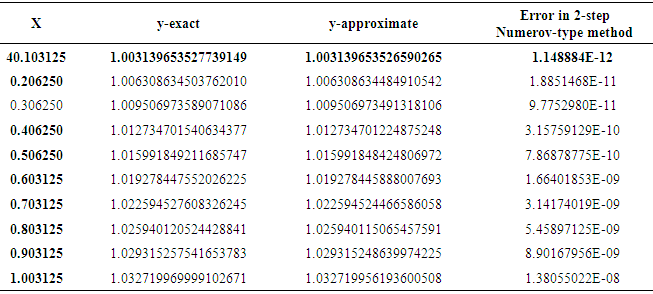
The theoretical solution is 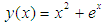 Tables 1 and 2 showed the y-exact, y-approximate and the error in one-step and two-step Numerov-type method for the non-linear problem 1.
Tables 1 and 2 showed the y-exact, y-approximate and the error in one-step and two-step Numerov-type method for the non-linear problem 1.Table 1. The y-exact, approximate solution and error in One-step Numerov-type method for the non-linear problem 1
 |
| |
|
Table 2. The y-exact, approximate solution and error in 2-step method for the non-linear problem 1
 |
| |
|
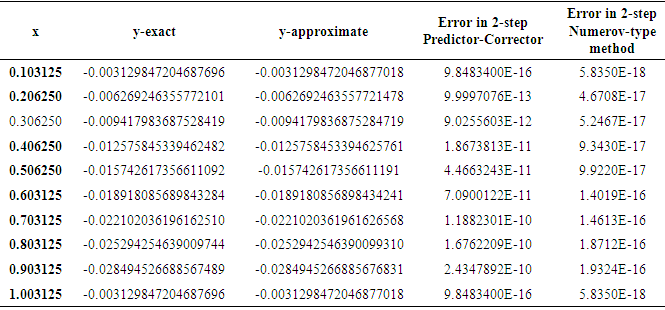
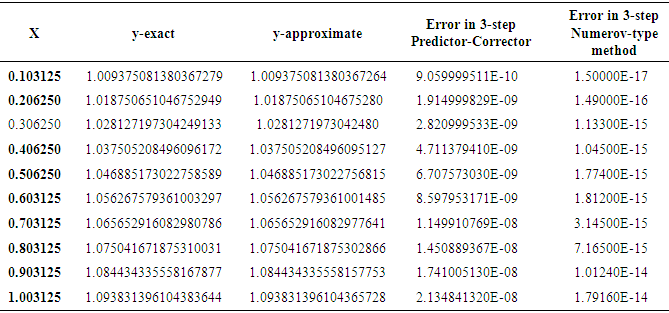
It could be seen from tables 3, 4 and 5 that the maximum absolute error of the new Implicit Hybrid Block Numerov-type methods when they were implemented in block-mode are higher (more accurate) than those of maximum absolute error of the predictor -corrector mode for problems 2, 3 and 4.Table 3. Accuracy Comparison of the 2-step Predictor-Corrector and 2-step Implicit Numerov-type method for linear problem 2
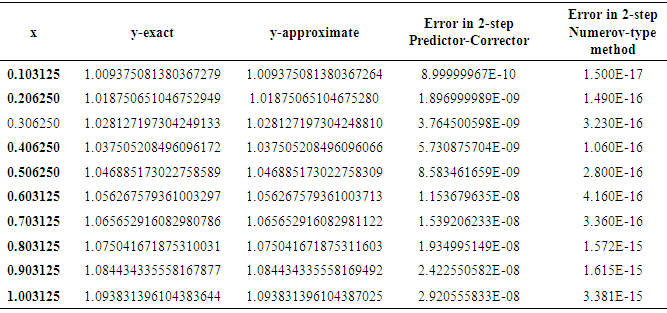 |
| |
|
Table 4. Accuracy Comparison of the 2-step Predictor-Corrector and 2-step Implicit Numerov-type method for problem 3
 |
| |
|
Table 5. Accuracy Comparison of the 3-step Predictor-Corrector and 3-step Implicit Numerov-type method for problem 4
 |
| |
|
5. Conclusions
The Numerov’s method which was initially designed for special second order initial value problems was modified in this paper to handle and solve general fourth order initial value problems of ordinary differential equations. The derived methods were implemented both in block and predictor-corrector mode. The block methods have the advantages of being self starting, are uniformly of the same order of accuracy and do not need predictors, having good accuracy as shown on numerical results of tables 3, 4 and 5. It should be noted that accuracy and efficiency rate of a method is dependent on the implementation strategies. If economical computation is required, then the new block methods are the better choice. The block method is recommended for general purposed use. Finally, the region of absolute stability of the block methods of one-step method, two-step method and three-step method were presented in figure 1, 2 and 3. Maple and Matlab software package were employed to generate the schemes and results.
References
| [1] | Adee, S. O. Onumanyi, P. Serisina, W and Yahaya Y. A (2005) Note on Starting the Numerov Method More Accurately by a Hybrid Formula of Order Four for Initial Value Problems. Journal of Computational and applied mathematics, 175,369-373. |
| [2] | Akinfenwa, O. A. Yao, N.M. Jator, S. N. (2011) Implicit Two Step Continuous Hybrid Block Methods with Four Off-Steps Points for Solving Stiff Ordinary Differential Equation. World Academy of Science, Engineering and Technology. International Scholarly and Scientific Research & Innovation, 5(3) 282-285. |
| [3] | Awari , Y. S. Abada, A. A. Emma, P.M. Kamoh, N. M. (2013) Application of Two-step Continuous Hybrid Butcher’s Method in Block Form for The Solution Of First order Initial Value Problem. Natural and Applied Sciences 4(4), 209-217. |
| [4] | Awoyemi D. O and Idowu O. M (2005) A Class of Hybrid Collocation Methods for Third–Order Ordinary Differential Equations. International Journal of Computer Mathematics. Vol 82, No 00, 1-7. DOI;10.1080/0027160500112902. |
| [5] | Butcher, J. C (1987) The Numerical Analysis of Ordinary Differential Equations, Runge-Kutta and General Linear Methods. Wiley, New York. |
| [6] | Dahlquist, G (1956) Convergence and stability in the numerical integration of Ordinary Differential Equations. Math, Scand, 4, 33-53. |
| [7] | Fatunla, S. O (1991) Block Method for Second Order Ordinary Differential Equations. International Journal of Computer Mathematics, 41(1 &2), 55-63. |
| [8] | Fatunla, S. O (1994). Block Methods for Second Order IVPs. Inter. J.Compt. Maths 41, 55-63. |
| [9] | Gear, C.W (1965) Hybrid Methods for Initial Value Problems in Ordinary Differential Equations. SIAM, J. Numer. Anal., 2 (1965), 69–86. |
| [10] | Hairer, E and Wanner, G (1996) Solving Ordinary Differential Equations II, Stiff and Differential–Algebraic Problems second revised edition ISBN3-540-60452-9 Springer-Verlag Berlin Heidelberg New York. 241. |
| [11] | Hans Van de Vyver (2007) An Explicit Numerov-type Method for Second-Order Differential Equations with Oscillating Solutions. An International Journal of Computers and Mathematics with, Applications, 53(2007), 1339–1348. doi:10.1016/j.camwa.2006.06.012. |
| [12] | Lambert, J. D (1973) Computational Methods in Ordinary Differential Equations. |
| [13] | Lambert, J. D (1991) Numerical Methods for Ordinary Differential Systems. John Wiley, New York. |
| [14] | Laudau, L. D. & Liftshitz F. M (1989) Quantum Mechanics Pergamon, New York. |
| [15] | Liboff, R. L (1980) Introductory Quantum Mechanics, Addison-Wiley, Reading M. A 1980. |
| [16] | Sirisena, U. W, Kumleng, G. M. Yahaya Y. A (2004) A Butcher-type Two-Step Hybrid Multistep Method for Accurate and Efficient Parallel Solution of ODEs. The Journal of the Mathematical Association of Nigeria Vol. 31, No 2A Mathematics series. |
| [17] | Thompson, D and Gonzalez Quiroz J. L M. (1997) Getting Started with Numerov methods. Computer in Physics,11(5); 514-515, American Institute of Physis inc. Woodbury NY,USA. doi:10.1063/1.168593. |
| [18] | Vigo-Aguiar and Ramos (2005) A Variable-Step Numerov Method for the Numerical Solution of the Schrodinger Equations. Journal of Mathematical Chemistry. 37(3), DOI: 10.1007/s10910-004-1467-3. |

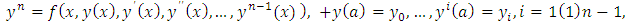
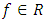 is sufficiently differentiable and satisfies a Lipschitz condition. This class of problems has a wide variety of applications in science and engineering field especially in mechanical systems without dissipation, control theory and celestial mechanics (see Laudau and Liftshitz (1989); Liboff (1980)). However, only a limited number of analytical methods are available for solving (1) directly without reducing it to a first order system of differential equations. There exists an extensive literature on numerical methods for the solution of ordinary differential equations (see, for example Lambert (1973, 1976, 1991), Adee et al., (2005), Awoyemi and Idowu (2005), Twizell and Khaliq (1984) and Sirisena et al., (2004)). In particular, Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third–order ordinary differential equations. Sirisena et al., (2004)) constructed a Butcher- type two-step hybrid multistep method for accurate and efficient parallel solution of ordinary differential equations.Hybrid methods were first proposed to overcome the Dahlquist (1956) barrier theorem whereby the conventional linear multistep method was modified to incorporating off-step points of derivation process (see Lambert (1973) and Gear (1965)). They utilize data at other points, other than the step points
is sufficiently differentiable and satisfies a Lipschitz condition. This class of problems has a wide variety of applications in science and engineering field especially in mechanical systems without dissipation, control theory and celestial mechanics (see Laudau and Liftshitz (1989); Liboff (1980)). However, only a limited number of analytical methods are available for solving (1) directly without reducing it to a first order system of differential equations. There exists an extensive literature on numerical methods for the solution of ordinary differential equations (see, for example Lambert (1973, 1976, 1991), Adee et al., (2005), Awoyemi and Idowu (2005), Twizell and Khaliq (1984) and Sirisena et al., (2004)). In particular, Awoyemi and Idowu (2005) developed a class of hybrid collocation methods for third–order ordinary differential equations. Sirisena et al., (2004)) constructed a Butcher- type two-step hybrid multistep method for accurate and efficient parallel solution of ordinary differential equations.Hybrid methods were first proposed to overcome the Dahlquist (1956) barrier theorem whereby the conventional linear multistep method was modified to incorporating off-step points of derivation process (see Lambert (1973) and Gear (1965)). They utilize data at other points, other than the step points 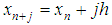 . Hybrid methods increase the order of the method while preserving good stability properties. Thompson and Gonzalez (1997) described Numerov’s method as an efficient and one of the most widely used algorithms for solving special second order linear ordinary differential equations of the form
. Hybrid methods increase the order of the method while preserving good stability properties. Thompson and Gonzalez (1997) described Numerov’s method as an efficient and one of the most widely used algorithms for solving special second order linear ordinary differential equations of the form 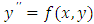 . He gave the following examples; one-dimensional time- independent
. He gave the following examples; one-dimensional time- independent 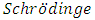 equation, the equation of motion of an undamped forced harmonic oscillator and Poisson’s equations.Moreover, according to Vigo-Aguiar and Ramos (2005), different authors have dealt with
equation, the equation of motion of an undamped forced harmonic oscillator and Poisson’s equations.Moreover, according to Vigo-Aguiar and Ramos (2005), different authors have dealt with 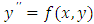 in providing different approaches to solving it, but the pioneer work was probably due to
in providing different approaches to solving it, but the pioneer work was probably due to 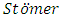 (Lambert (1973)), who developed his method in connection with numerical calculations concerning the aurora borealis. The k-step
(Lambert (1973)), who developed his method in connection with numerical calculations concerning the aurora borealis. The k-step 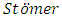 method may be derived similarly to the Adams method, by twice integrating the differential equation and then replacing f by the interpolating polynomial passing through the points
method may be derived similarly to the Adams method, by twice integrating the differential equation and then replacing f by the interpolating polynomial passing through the points 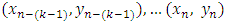 , where the
, where the 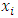 are equally spaced. However, to obtain more accurate formulas, it is possible used the interpolation polynomial passing through the additional points
are equally spaced. However, to obtain more accurate formulas, it is possible used the interpolation polynomial passing through the additional points 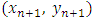 in which implicit
in which implicit 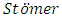 method was obtained (also known in certain contexts as the Cowell method or the Numerov method) (Vigo-Aguiar and Ramos (2005)). In Hans Van de Vyver (2007), an explicit Numerov-type method for second-order differential equations with oscillating solution was proposed. All authors mentioned above independently developed Numerov’s methods for the solution of special second order ordinary differential equations but little discussion was devoted to the modification of Numerov’s method to handle general higher order ordinary differential equations.In the research work of Awari et al., (2013), the application of two-step continuous hybrid Butcher’s method in block form for the solution of first order initial value problem was considered. Akinfenwa et al., (2011) derived implicit two step continuous hybrid block methods with four off-steps points for solving stiff ordinary differential equation. Therefore, this article proposes a class of continuous implicit hybrid block Numerov- type method for the direct solution of fourth order ordinary differential equations directly without reducing to system of first-order ordinary differential equations. The block methods can be seen as a set of linear multistep methods simultaneously applied to (1) and then combined to yield an approximation with better accuracy, better stability, better efficiency in parallel computing. λDefinition 1.1: The block method is said to be zero-stable if the roots
method was obtained (also known in certain contexts as the Cowell method or the Numerov method) (Vigo-Aguiar and Ramos (2005)). In Hans Van de Vyver (2007), an explicit Numerov-type method for second-order differential equations with oscillating solution was proposed. All authors mentioned above independently developed Numerov’s methods for the solution of special second order ordinary differential equations but little discussion was devoted to the modification of Numerov’s method to handle general higher order ordinary differential equations.In the research work of Awari et al., (2013), the application of two-step continuous hybrid Butcher’s method in block form for the solution of first order initial value problem was considered. Akinfenwa et al., (2011) derived implicit two step continuous hybrid block methods with four off-steps points for solving stiff ordinary differential equation. Therefore, this article proposes a class of continuous implicit hybrid block Numerov- type method for the direct solution of fourth order ordinary differential equations directly without reducing to system of first-order ordinary differential equations. The block methods can be seen as a set of linear multistep methods simultaneously applied to (1) and then combined to yield an approximation with better accuracy, better stability, better efficiency in parallel computing. λDefinition 1.1: The block method is said to be zero-stable if the roots 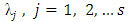 of the characteristic polynomial
of the characteristic polynomial 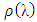 defined by
defined by 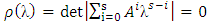 satisfies
satisfies 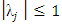 and for those roots with
and for those roots with 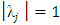 , the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals
, the multiplicity must not exceed the order of the differential equation. (see Fatunla (1994)). Definition 1.2: The set of W equals 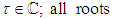
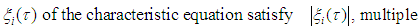
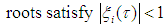 is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition 1.3: The LMM is said to be consistent if it has order
is called the stability region or region of absolute stability of the method (Hairer and Wanner (1996)).Definition 1.3: The LMM is said to be consistent if it has order 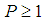 .The paper is organized as follows. Section 1 is of an introductory nature. The construction and implementation of the implicit hybrid block Numerov -type methods were described in Section 2. Stability analysis of the new methods was discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.
.The paper is organized as follows. Section 1 is of an introductory nature. The construction and implementation of the implicit hybrid block Numerov -type methods were described in Section 2. Stability analysis of the new methods was discussed in Section 3. In Section 4, some numerical experiments and results showing the relevance of the new methods are discussed. Finally, in Section 5 some conclusions are drawn.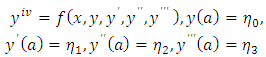
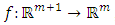 , y is an m-dimensional vector and
, y is an m-dimensional vector and  is a scalar variable and a set of equally spaced points on the integration interval also given by
is a scalar variable and a set of equally spaced points on the integration interval also given by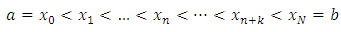 with a specified positive integer step number k greater than zero. In this work, h is assumed to be a constant step-size given by
with a specified positive integer step number k greater than zero. In this work, h is assumed to be a constant step-size given by 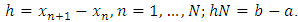 Assuming an approximate solution to (2) in form
Assuming an approximate solution to (2) in form 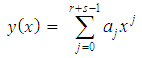
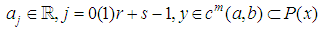 , r is the interpolation points and s is the collocation points. The highest derivative of (3) is given as:
, r is the interpolation points and s is the collocation points. The highest derivative of (3) is given as: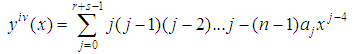
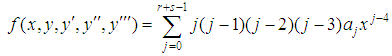
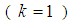 , we collocate (5) at
, we collocate (5) at 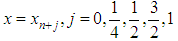 and interpolate (3) at
and interpolate (3) at 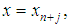
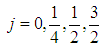 lead to system of equations with parameters
lead to system of equations with parameters 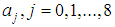 . Solving for these parameters and substituting into (3) using Maple software package, yields a linear multistep method with continuous coefficients of the form:
. Solving for these parameters and substituting into (3) using Maple software package, yields a linear multistep method with continuous coefficients of the form: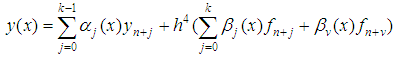
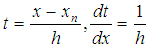 . The coefficients of
. The coefficients of 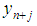 and
and 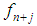 are obtained as:
are obtained as: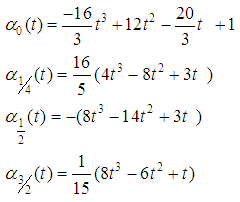

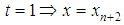 gives the discrete scheme:
gives the discrete scheme: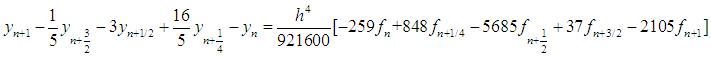
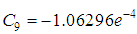 . The first, second and third derivatives of the continuous scheme (7) are found and evaluated at
. The first, second and third derivatives of the continuous scheme (7) are found and evaluated at 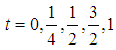 .Express explicitly as:
.Express explicitly as: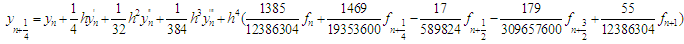
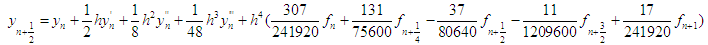
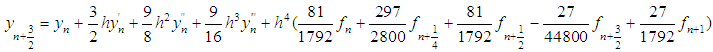
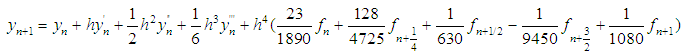
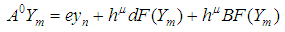
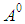 identity matrix, µ is the order of differential equation and
identity matrix, µ is the order of differential equation and
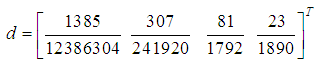
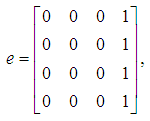
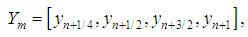
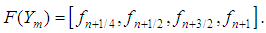
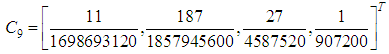
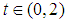 are independent and infinite are of uniform order of accuracy.Similarly, for two-step method (
are independent and infinite are of uniform order of accuracy.Similarly, for two-step method (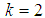 ), equation (5) is collocated at
), equation (5) is collocated at 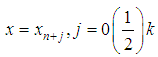 and equation (3) is interpolated at
and equation (3) is interpolated at 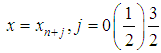 leads to a system of equations which after some manipulations yields the continuous method expressed in the form:
leads to a system of equations which after some manipulations yields the continuous method expressed in the form: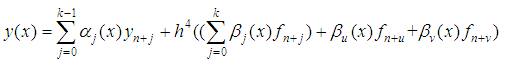
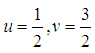 .The coefficients
.The coefficients 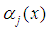 and
and 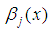 are expressed as functions of t .
are expressed as functions of t .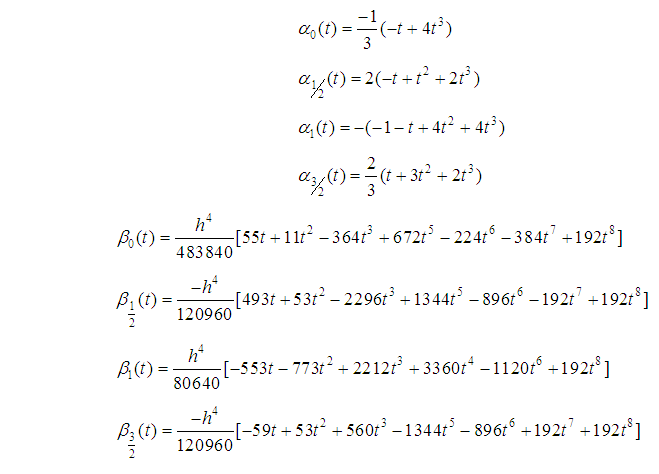
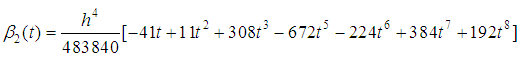
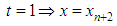 gives the discrete scheme
gives the discrete scheme 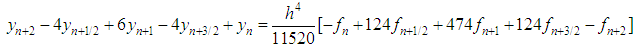
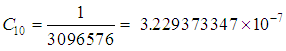 . The first, second and third derivatives of the continuous scheme (21) are found and evaluated at
. The first, second and third derivatives of the continuous scheme (21) are found and evaluated at 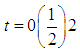 and after some manipulations gives the explicit discrete block schemes:
and after some manipulations gives the explicit discrete block schemes: 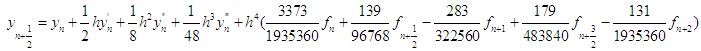
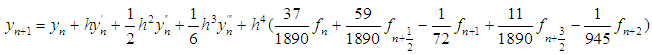
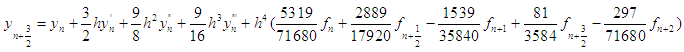

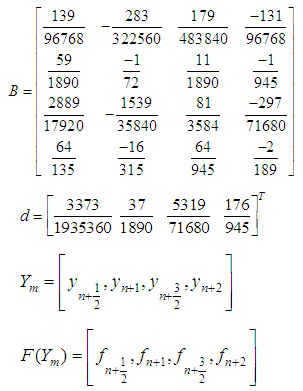
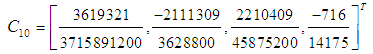
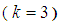 , collocation is done at
, collocation is done at 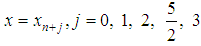 and interpolation is done at
and interpolation is done at 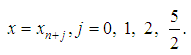 The continuous linear multistep method is given in the form:
The continuous linear multistep method is given in the form: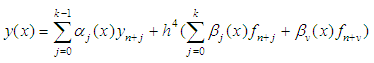
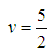 and the coefficients
and the coefficients 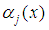 and
and 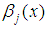 are expressed as.
are expressed as. 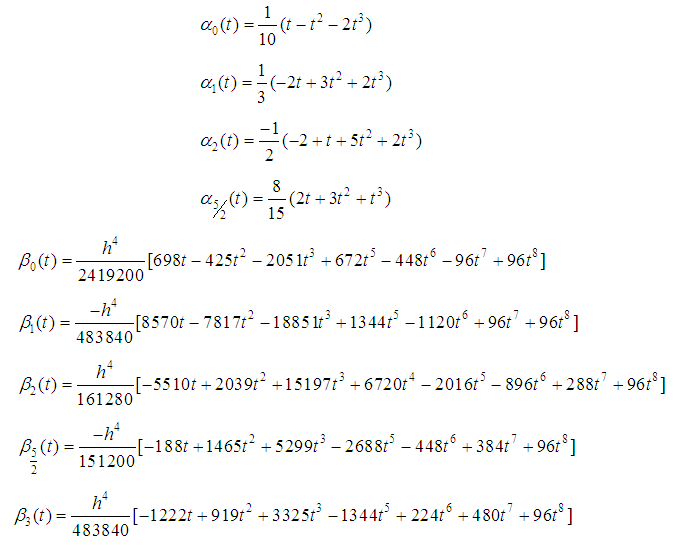
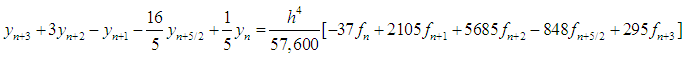
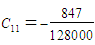 . The main discrete scheme and the additional schemes obtained are writing explicitly as:
. The main discrete scheme and the additional schemes obtained are writing explicitly as: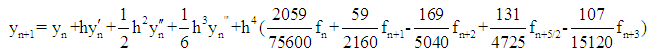
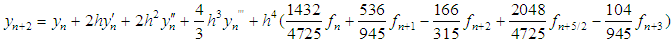
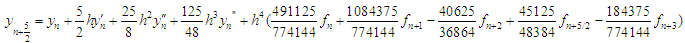
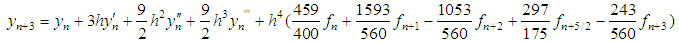
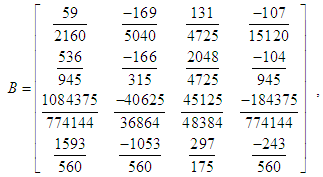

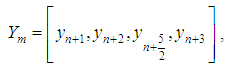
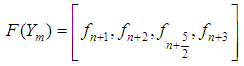
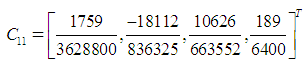

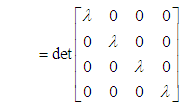
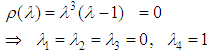 This satisfies the condition for method (13) to be zero –stable. Hence the block method is zero stable (see definition (1.1), (1.2) and (1.3). The block method is also consistent, as it has the order p greater than 1. Hence the convergence of the method is asserted as in the theorem 3.1 below.Theorem 3.1: (Dahlquist 1956)The necessary and sufficient conditions for a linear multistep to be convergent are that it be consistent and zero-stable.
This satisfies the condition for method (13) to be zero –stable. Hence the block method is zero stable (see definition (1.1), (1.2) and (1.3). The block method is also consistent, as it has the order p greater than 1. Hence the convergence of the method is asserted as in the theorem 3.1 below.Theorem 3.1: (Dahlquist 1956)The necessary and sufficient conditions for a linear multistep to be convergent are that it be consistent and zero-stable.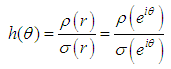 where
where  and
and 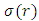 are the first and second characteristics polynomial respectively as:
are the first and second characteristics polynomial respectively as: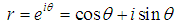 Using a Matlab program, the absolute stability region of the new methods is plotted below.
Using a Matlab program, the absolute stability region of the new methods is plotted below.


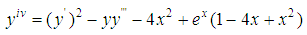 Subject to the initial condition
Subject to the initial condition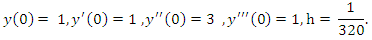 Problem 2
Problem 2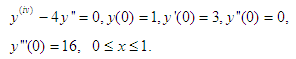 The theoretical solution is given as
The theoretical solution is given as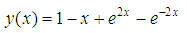 Problem 3
Problem 3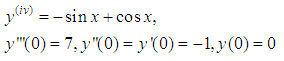 Exact Solution
Exact Solution 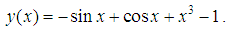 Problem 4Consider the non-homogeneous linear equation of fourth order below
Problem 4Consider the non-homogeneous linear equation of fourth order below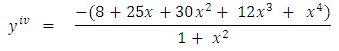 Subject to the initial conditions
Subject to the initial conditions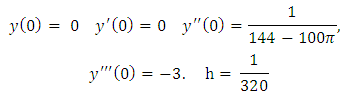 The theoretical solution is
The theoretical solution is 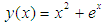 Tables 1 and 2 showed the y-exact, y-approximate and the error in one-step and two-step Numerov-type method for the non-linear problem 1.
Tables 1 and 2 showed the y-exact, y-approximate and the error in one-step and two-step Numerov-type method for the non-linear problem 1. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML



