K. Maruthi Prasad 1, N. Subadra 2, M. A. S. Srinivas 3
1Department of Engineering Mathematics, GITAM University, Hyderabad Campus, Hyderabad, Telangana, India
2Department of Mathematics, Geethanjali College of Engg. & Tech., Cheeryal (V), Keesara (M), R.R. Dist., Telangana, India
3Department of Mathematics, Jawaharlal Nehru Technological University, Kukatpally, Hyderabad, Telangana, India
Correspondence to: K. Maruthi Prasad , Department of Engineering Mathematics, GITAM University, Hyderabad Campus, Hyderabad, Telangana, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Peristaltic transport of a nanofluid in an inclined tube under the assumption of long wave length and low Reynolds number has been investigated. The coupled equations in temperature profile and nanoparticle phenomena are solved by using Homotopy Perturbation Method. Byusing this method the closed form solutions of pressure drop, time averaged flux and frictional force have been calculated. It is found that the pressure drop increases with the Brownian motion parameter 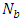 but decreases with the thermophoresis number
but decreases with the thermophoresis number 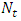 and inclination
and inclination 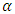 . It is also found that the pressure drop decreases with wave amplitude and increases with wave length. The frictional force increases with Brownian motion parameter
. It is also found that the pressure drop decreases with wave amplitude and increases with wave length. The frictional force increases with Brownian motion parameter 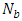 , wavelengthand decreases with the thermophoresis number
, wavelengthand decreases with the thermophoresis number 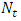 , inclination
, inclination 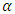 and wave amplitude. It can be seen that, thattemperature profile decreases with the Brownian motion parameter
and wave amplitude. It can be seen that, thattemperature profile decreases with the Brownian motion parameter 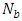 and increases with the thermophoresis number
and increases with the thermophoresis number 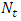 . Thenanoparticle phenomena increases with the Brownian motion parameter
. Thenanoparticle phenomena increases with the Brownian motion parameter 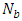 and decreases with the thermophoresis number
and decreases with the thermophoresis number 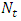 . It is observed that, the maximum pressure gradient occurs for different values of wave amplitude for sinusoidal, multi sinusoidal, triangular, trapezoidal and square waves. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
. It is observed that, the maximum pressure gradient occurs for different values of wave amplitude for sinusoidal, multi sinusoidal, triangular, trapezoidal and square waves. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
Keywords:
Peristalsis, Nanofluid, Homotopy perturbation method, Brownian motion parameter, Thermophoresis number
Cite this paper: K. Maruthi Prasad , N. Subadra , M. A. S. Srinivas , Peristaltic Transport of a Nanofluid in an Inclined Tube, American Journal of Computational and Applied Mathematics , Vol. 5 No. 4, 2015, pp. 117-128. doi: 10.5923/j.ajcam.20150504.04.
1. Introduction
The study of peristaltic transport has received considerable attention in the recent past, as it is known to be one of the main mechanisms for fluid transport in biological systems. It is found that physiological flows are maintained by sinusoidal pressure gradient as well as motion of the boundaries. Peristaltic transport widely occurs in many biological systems as well as in many industries. For example, food swallowing through the esophagus, intra-urine fluid motion, circulation of blood in small blood vessels, the flow of many other glandular ducts and toxic liquid transportation in the nuclear industry etc.Peristalsis was first studied by Latham [11] in 1965. He analyzed the fluid motion in a peristaltic pump. Several investigators have contributed to the study of peristaltic motion in both mechanical and physiological situations. Shaprio et al. [20], Fungand Yih [5], Radhkrishnamacharya and Srinivasulu [19], Misra et al. [16], Mekheimer [15].Though all the above investigations consider the fluid to be Newtonian, some researchers studiedperistaltic transport of non-Newtonian fluids also: Devi and Devanathan [4], SrivastavaandSrivastava [21], Muthu et al. [17], Maruthi Prasad and Radhakrishnamacharya [12]. Maruthi Prasad et al. [14] studied unsteady peristaltic flow of a viscous fluid in a two dimensional curved channel. In recent days many researchers have focused their attention on the study of nanofluid for different flow geometries. Choi [2] was first person who initiated to study the nanofluid technology. A detailed examination of nanofluid was discussed by Buongiorno J [1] in Convective transport in nanofluids. Das et al. [3] studied Pool boiling of nanofluids on horizontal narrow tubes. Noreen Sher Akbar et al. [18] studied Peristaltic flow of a nanofluid in a non-uniform tube. They analyzed the temperature profile and nanoparticle phenomena using homotopy perturbation technique. Khan and Pop [9] studied boundary layer flow of a nanofluid passing a stretching sheet.It is known that many ducts in physiological systems are not horizontal but have some inclination with the axis. Maruthi Prasad K et al. [13] studied Peristaltic pumping of a micropolar fluid in an inclined tube. However, the study of peristaltic transport of a nanofluid in an inclined tube has not been studied. Motivated by these studies, the peristaltic pumping of a nanofluid in an inclined tube under the assumption of long wavelength and low Reynolds number is investigated. The resulting equations of the temperature profile and nanoparticle phenomena are solved using homotopy perturbation technique. The analytical solutions of velocity, pressure drop and frictional forces are obtained. The effects of various parameters on these flow variables are investigated. The pressure gradient versus sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square wave are presented graphically. The stream lines for sinusoidal wave and multi sinusoidal waves are represented graphically at the end.
2. Physical Model and Fundamental Equations
Equations for an incompressible fluid for the balance of mass, momentum, temperature and nanoparticle volume fraction are given by [10]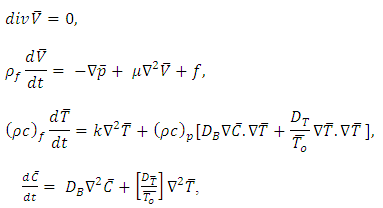 where
where 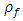 is the density of the fluid,
is the density of the fluid, 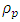 is the density of the particle,
is the density of the particle, 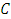 is the volumetric volume expansion coefficient,
is the volumetric volume expansion coefficient, 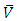 is the velocity vector,
is the velocity vector, 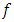 is the body forces,
is the body forces, 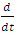 represents the material time derivative ,
represents the material time derivative , 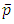 is the pressure,
is the pressure, 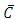 is the nanoparticle phenomena,
is the nanoparticle phenomena, 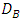 is the Brownian diffusion coefficient and
is the Brownian diffusion coefficient and 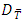 is the thermophoretic diffusion coefficient. The ambient values of
is the thermophoretic diffusion coefficient. The ambient values of 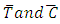 as
as 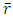 tend to
tend to 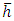 are denoted by
are denoted by 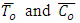 .
.
3. Mathematical Formulation
Consider the peristaltic motion of an incompressible nanofluid in an inclined tube of uniform cross-section of radius 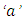 with sinusoidal waves travelling along the tube with speed
with sinusoidal waves travelling along the tube with speed 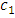 , amplitude
, amplitude 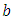 and wave length
and wave length 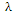 . Further suppose the tube is inclined at an angle
. Further suppose the tube is inclined at an angle 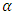 with the horizontal axis as shown in Figure 1. Heat transfer and nano-particle phenomena are considered. At the center of the tube, symmetry condition is used on both temperature and concentration, while the walls of the tube maintain temperature
with the horizontal axis as shown in Figure 1. Heat transfer and nano-particle phenomena are considered. At the center of the tube, symmetry condition is used on both temperature and concentration, while the walls of the tube maintain temperature 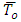 and nanoparticle volume fraction
and nanoparticle volume fraction 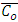 .
.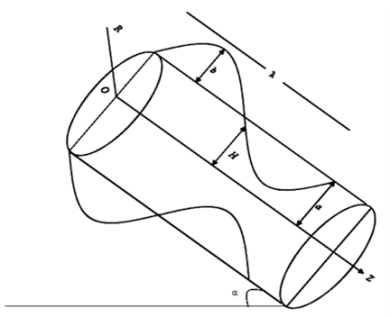 | Figure 1. Peristaltic transport in an inclined tube |
The geometry of the wall surface is defined as 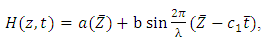 | (1) |
where 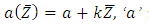 is the radius of the inlet,
is the radius of the inlet, 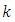 is the constant whose magnitude depends on the length of the tube and
is the constant whose magnitude depends on the length of the tube and 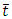 is the time. Cylindrical coordinate system
is the time. Cylindrical coordinate system 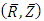 is chosen, so that
is chosen, so that 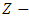 axis coincides with the center line of the tube and
axis coincides with the center line of the tube and 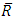 is transverse to it. Further, the flow is assumed to be axisymmetric.Using the transformations
is transverse to it. Further, the flow is assumed to be axisymmetric.Using the transformations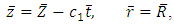 | (2) |
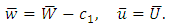 | (3) |
From a stationary to a moving frame of reference, where 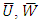 and
and 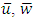 are velocity components in the radial and axial directions in the fixed and moving frames respectively, the governing equations in a fixed frame for an incompressible nanofluid in an inclined tube are given by
are velocity components in the radial and axial directions in the fixed and moving frames respectively, the governing equations in a fixed frame for an incompressible nanofluid in an inclined tube are given by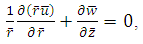 | (4) |
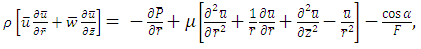 | (5) |
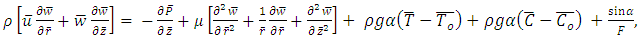 | (6) |
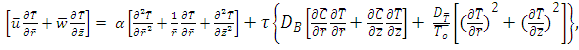 | (7) |
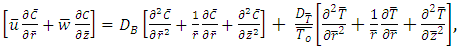 | (8) |
where 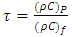 is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid.The boundary conditions in the wave frame are as follows
is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid.The boundary conditions in the wave frame are as follows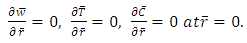 | (9) |
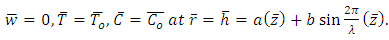 | (10) |
The following are non-dimensional variables: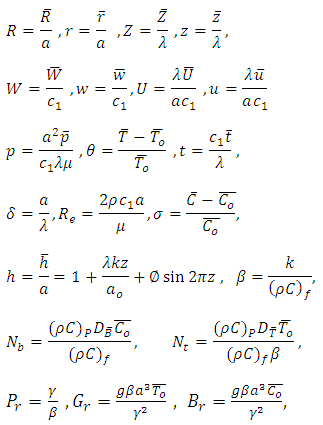 | (11) |
in which 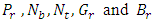 are the Prandtl number, the Brownian motion parameter, the thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number.Introducing the non-dimensional variables into equations (4)-(10) under the assumption of long wave length and low Reynolds number approximations, the equations (4)-(10) reduces to
are the Prandtl number, the Brownian motion parameter, the thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number.Introducing the non-dimensional variables into equations (4)-(10) under the assumption of long wave length and low Reynolds number approximations, the equations (4)-(10) reduces to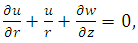 | (12) |
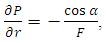 | (13) |
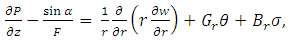 | (14) |
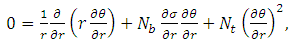 | (15) |
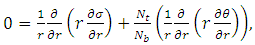 | (16) |
From equation (13) it is clear that 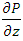 is a function of z only.The non-dimensional boundary conditions are
is a function of z only.The non-dimensional boundary conditions are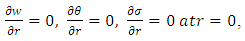 | (17a) |
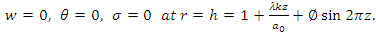 | (17b) |
4. Solution
The combination of the homotopy method and perturbation method is called Homotopy Perturbation Method (HPM). This method eliminates the drawbacks present in the traditional perturbation method and at the same time all the advantages remain the same.The homotopy for the equations (15) and (16) are as follows [6-8]: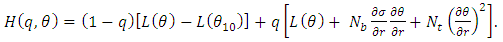 | (18) |
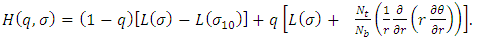 | (19) |
For convenience, 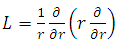 is taken as linear operator.
is taken as linear operator.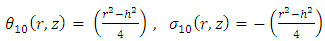 | (20) |
are defined as initial guesses which satisfy the boundary conditions.Define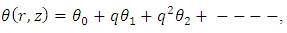 | (21) |
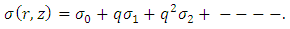 | (22) |
The series (21) and (22) are convergent for most of the cases. The convergent rate depends on the nonlinear part of the equation.Adopting the same procedure as done by HeJH [6-8], the solution for temperature and nanoparticle phenomena can be written for q=1 as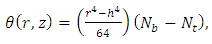 | (23) |
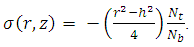 | (24) |
Substituting the equations (23) and (24) in the equation (14) and applying boundary conditions, the closed form of analytical solution for velocity can be written as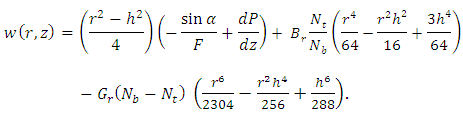 | (25) |
The dimension less flux q in the moving frame is given by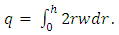 | (26) |
By substituting equation (25) in equation (26), the flux value will be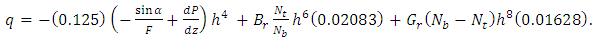 | (27) |
From equation (27), 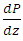 can be written as
can be written as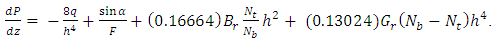 | (28) |
The pressure drop over a wave length 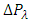 is defined by
is defined by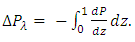 | (29) |
Substituting equation (28) in equation (29), 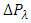 can be written as
can be written as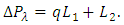 | (30) |
Where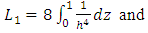 | (31) |
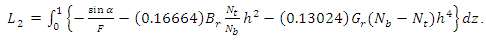 | (32) |
Following the analysis of Shapiro et al [20], the time averaged flux over a period in the laboratory frame 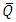 is given by
is given by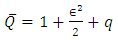 | (33) |
Substituting the value of q from equation (30) to equation (33), the equation of time averaged flux can be written as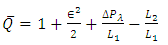 | (34) |
The dimensionless friction force 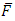 at the wall is given by
at the wall is given by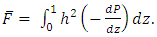 | (35) |
Five wave forms have been considered for analysis of pressure gradient namely sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves. The non-dimensional expressions for these wave forms are as follows:1. Sinusoidal Wave: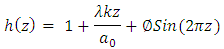 2. Multi Sinusoidal Wave:
2. Multi Sinusoidal Wave: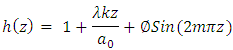 3. Triangular Wave:
3. Triangular Wave: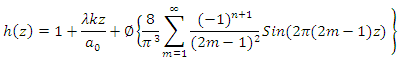 4. Trapezoidal Wave:
4. Trapezoidal Wave: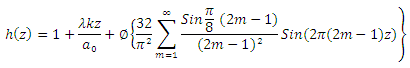 5. Square Wave:
5. Square Wave: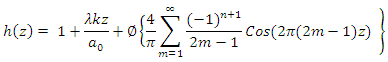
5. Results and Discussions
Analytical solutions for pressure drop 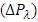 , time averaged flux
, time averaged flux 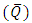 and frictional forces
and frictional forces 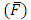 are given by the equations (23), (34) and (35) respectively. The effects of various parameters on pressure drop
are given by the equations (23), (34) and (35) respectively. The effects of various parameters on pressure drop 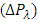 , time averaged flux
, time averaged flux 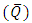 , frictional force
, frictional force 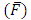 , temperature profile and nanoparticle phenomena have been calculated numerically by using Mathematica 9.0 software and the results are graphically presented in figures 2(a)-5(b). The pressure gradient for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves has been graphically represented from figures 6(a)-6(e). Stream lines for sinusoidal and multi sinusoidal waves are represented from figures 7(a)-7(b).The effects of various parameters on the pressure drop
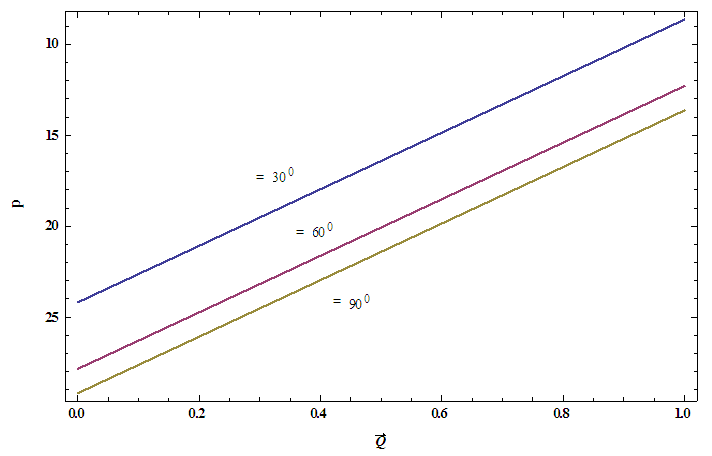
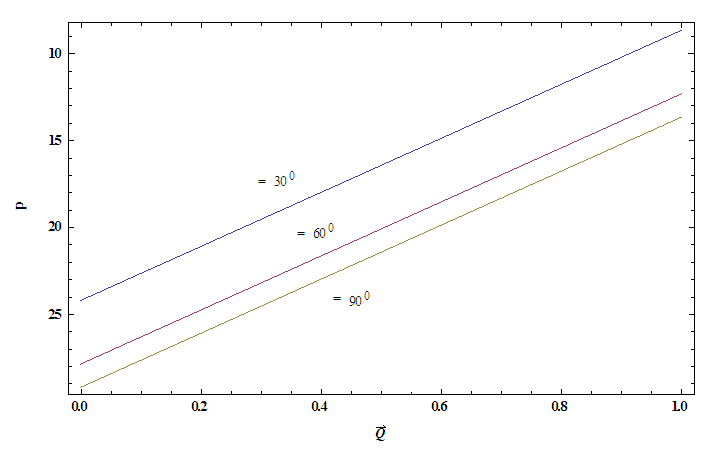
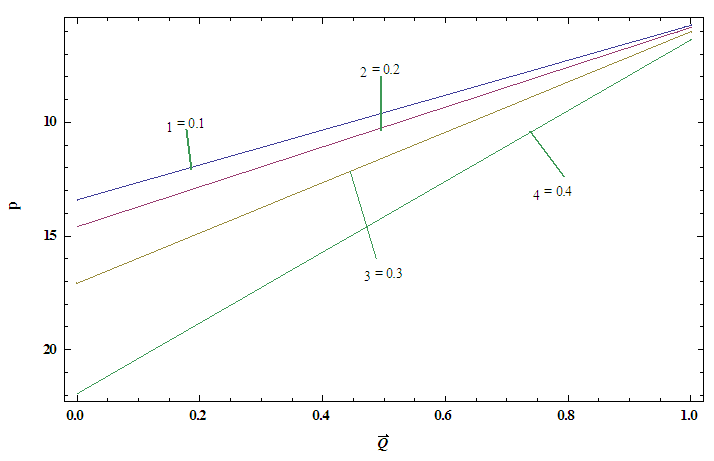
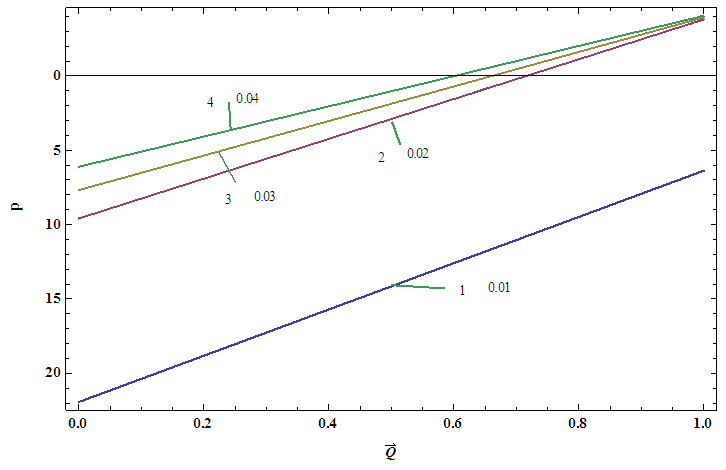
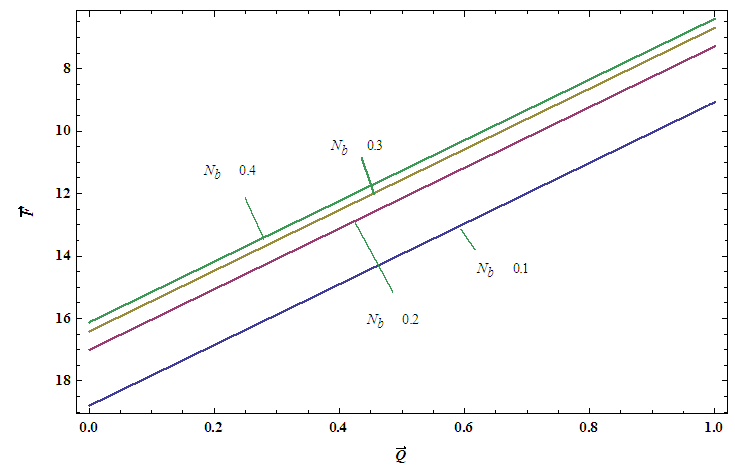
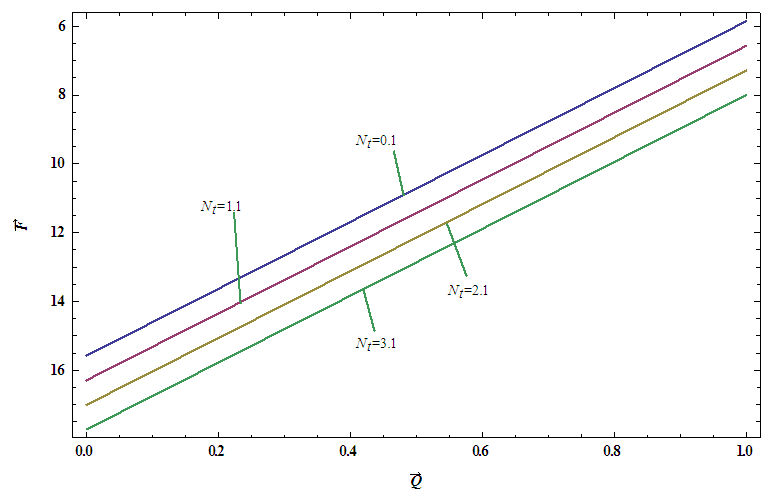
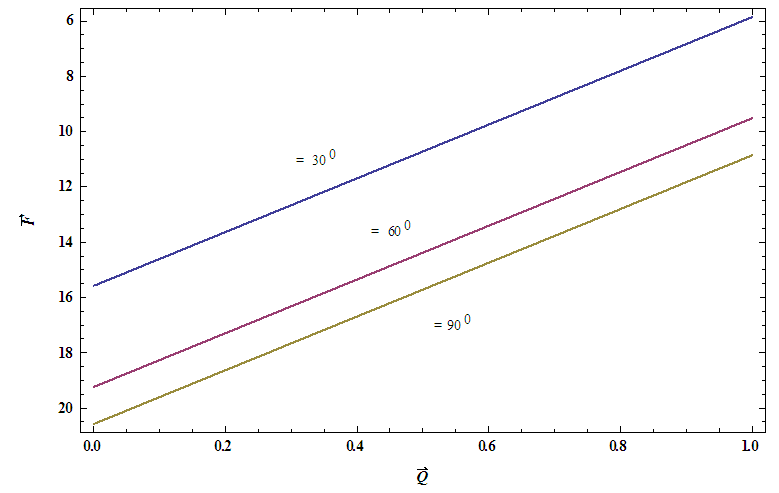
, temperature profile and nanoparticle phenomena have been calculated numerically by using Mathematica 9.0 software and the results are graphically presented in figures 2(a)-5(b). The pressure gradient for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves has been graphically represented from figures 6(a)-6(e). Stream lines for sinusoidal and multi sinusoidal waves are represented from figures 7(a)-7(b).The effects of various parameters on the pressure drop 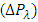 are shown in figures 2(a)-2(e), for various values of Brownian motion number
are shown in figures 2(a)-2(e), for various values of Brownian motion number 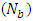 , thermophoresis parameter
, thermophoresis parameter 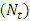 , inclination
, inclination 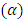 , wave length
, wave length  and wave amplitude
and wave amplitude 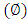 . It is observed that pressure drop increases with Brownian motion number
. It is observed that pressure drop increases with Brownian motion number 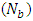 but decreases with thermophoresis parameter
but decreases with thermophoresis parameter 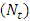 and inclination
and inclination 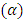 . Pressure drop
. Pressure drop 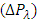 decreases with wave amplitude
decreases with wave amplitude 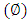 and increases with wave length
and increases with wave length 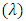 but it is interesting to note that the pressure drop converges to a particular value when the value of
but it is interesting to note that the pressure drop converges to a particular value when the value of 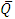 exceeds 1.Figures 3(a)-3(e) represent the behaviour of frictional force
exceeds 1.Figures 3(a)-3(e) represent the behaviour of frictional force 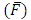 for different values of Brownian motion number
for different values of Brownian motion number 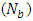 , thermophoresis parameter
, thermophoresis parameter 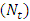 , inclination
, inclination 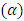 , wave length
, wave length 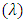 and wave amplitude
and wave amplitude 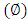 . It is observed that frictional force increases with the Brownian motion number
. It is observed that frictional force increases with the Brownian motion number 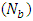 but decreases with the thermophoresis parameter
but decreases with the thermophoresis parameter 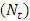 and inclination
and inclination 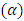 . Frictional force
. Frictional force 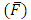 decreases with wave amplitude
decreases with wave amplitude 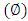 and increases with wave length
and increases with wave length 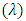 but converges to a particular value when
but converges to a particular value when 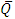 exceeds 1.It can be seen from figures 4(a)-4(b) that, temperatureprofile
exceeds 1.It can be seen from figures 4(a)-4(b) that, temperatureprofile 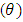 decreases with the Brownian motion parameter
decreases with the Brownian motion parameter 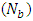 whereas increases with the thermophoresis parameter
whereas increases with the thermophoresis parameter 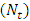 .Nanoparticle phenomena
.Nanoparticle phenomena 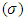 has been shown from figures 5(a)-5(b) for different values of Brownian motion number
has been shown from figures 5(a)-5(b) for different values of Brownian motion number 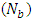 and thermophoresis parameter
and thermophoresis parameter 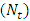 . It is observed that nanoparticle phenomena increases with the Brownian motion parameter
. It is observed that nanoparticle phenomena increases with the Brownian motion parameter 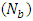 but decreases with the thermophoresis parameter
but decreases with the thermophoresis parameter 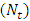 . From the graphs it is interested to note that the temperature profile has an opposite behaviour as compared to the nanoparticle phenomena.Pressure gradient
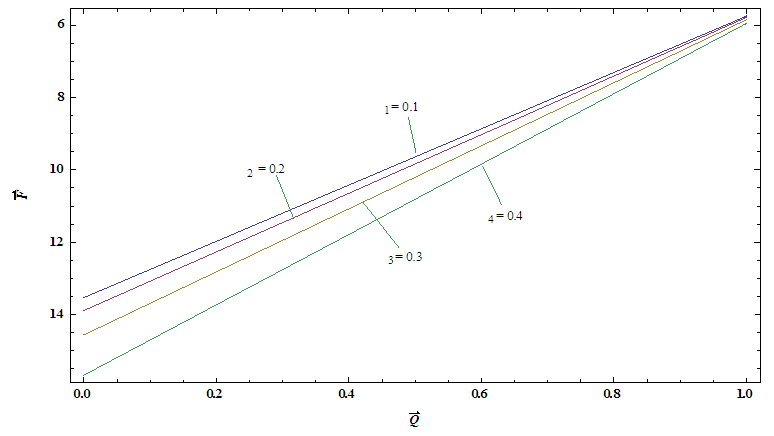
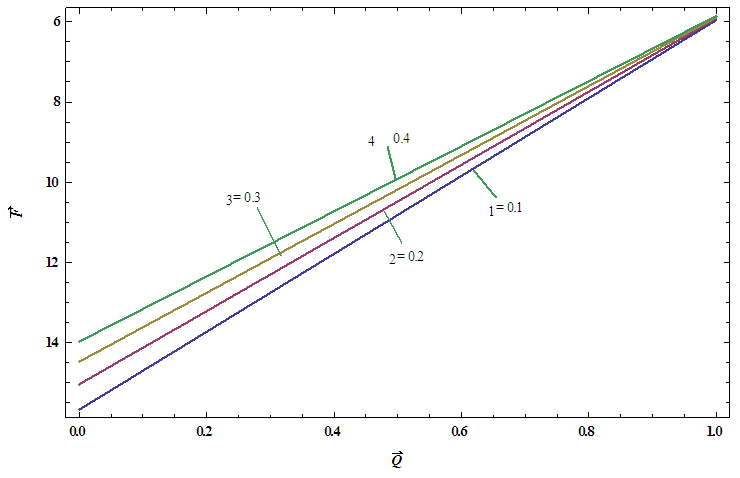
. From the graphs it is interested to note that the temperature profile has an opposite behaviour as compared to the nanoparticle phenomena.Pressure gradient 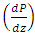 has been presented from figures 6(a)-6(e) for different values of wave amplitude
has been presented from figures 6(a)-6(e) for different values of wave amplitude 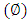 for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves. Maximum pressure gradient occurs in sinusoidal wave, triangular wave and trapezoidal waves for
for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves. Maximum pressure gradient occurs in sinusoidal wave, triangular wave and trapezoidal waves for 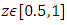 but interestingly for square wave pressure gradient
but interestingly for square wave pressure gradient 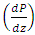 is maximum for
is maximum for 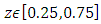 whereas for multi sinusoidal wave, the pressure gradient
whereas for multi sinusoidal wave, the pressure gradient 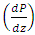 is maximum for
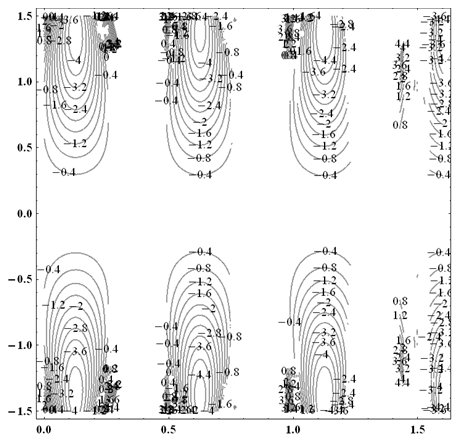
is maximum for  .Figures 7(a)-7(b) shows streamlines for sinusoidal and multi sinusoidal waves. It is noticed that the size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
.Figures 7(a)-7(b) shows streamlines for sinusoidal and multi sinusoidal waves. It is noticed that the size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.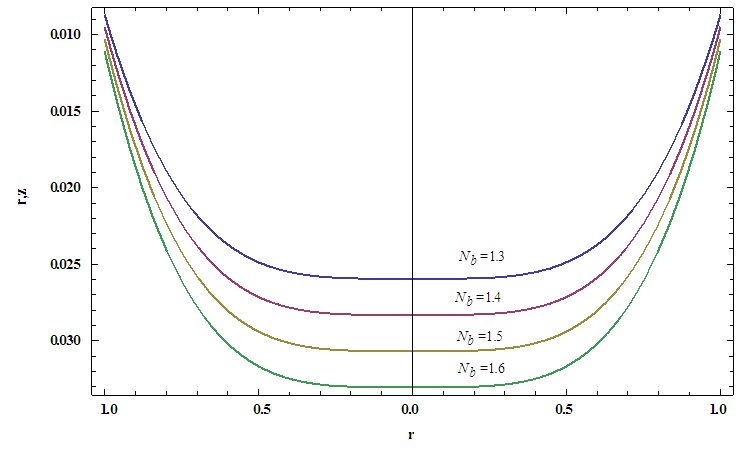 | Figure 4(a).  |
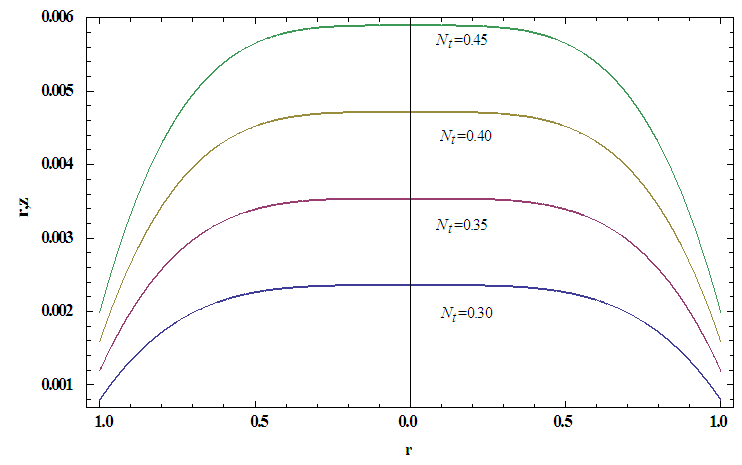 | Figure 4(b). 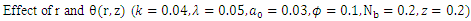 |
 | Figure 5(a). 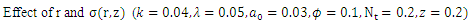 |
 | Figure 5(b). 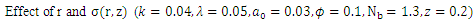 |
 | Figure 6(a). Pressure gradient versus Sinusoidal wave  |
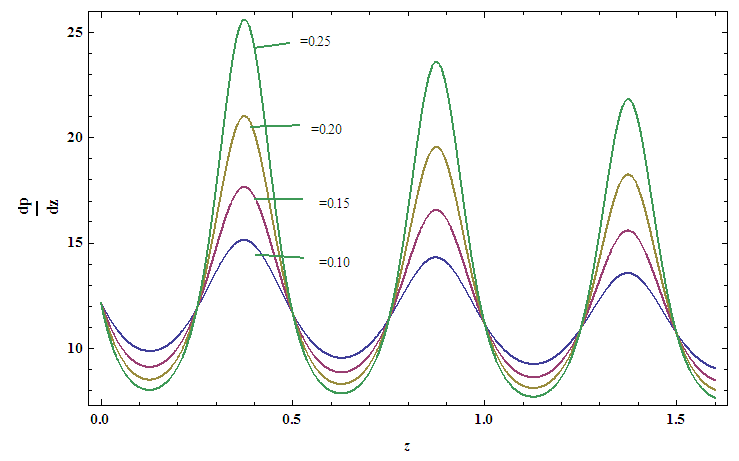 | Figure 6(b). Pressure gradient versus multi Sinusoidal wave 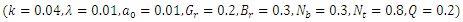 |
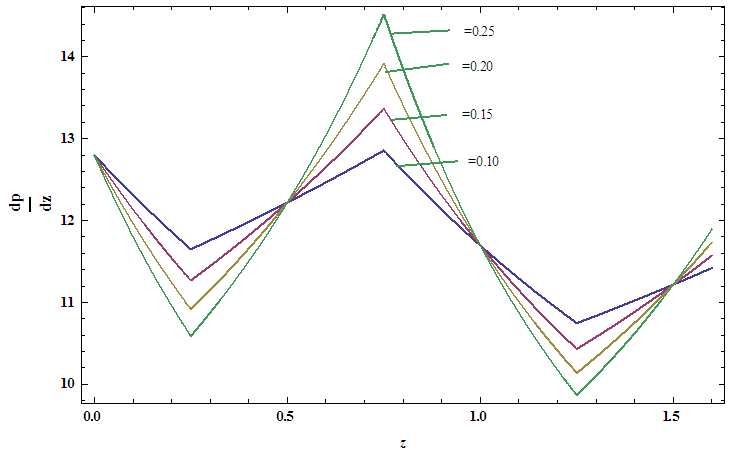 | Figure 6(c). Pressure gradient versus Triangular wave  |
 | Figure 6(d). Pressure gradient versus Trapezoidal wave 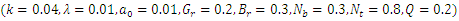 |
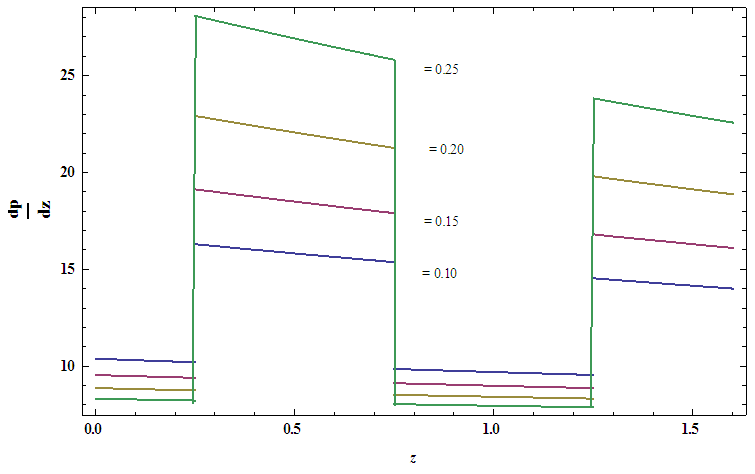 | Figure 6(e). Pressure gradient versus Square wave 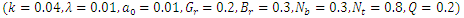 |
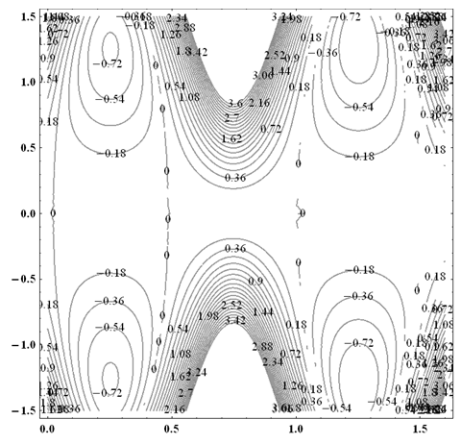 | Figure 7(a). Stream lines for Sinusoidal wave 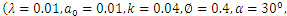 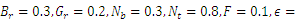 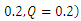 |
 | Figure 7(b). Stream lines for Multi Sinusoidal wave 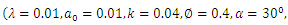 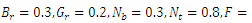 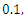  |
6. Conclusions
This study examines the peristaltic transport of a nanofluid passing through an inclined tube under the long wave length and low Reynolds number assumptions. Temperature profile and nanoparticle phenomena have been calculated using Homotopy Perturbation technique while analytical solutions have been calculated for velocity profile, pressure drop, time averaged flux and frictional force. Pressure gradient versus wave amplitude for various waves have been represented.The main points of the analysis are as follows:a. The pressure drop increases with the Brownian motion number 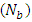 , whereas decreases with the thermophoresis parameter
, whereas decreases with the thermophoresis parameter 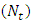 and inclination
and inclination 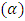 . Pressure drop decreases with wave amplitude
. Pressure drop decreases with wave amplitude 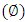 and increases with wave length
and increases with wave length 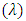 but converges to a certain point after
but converges to a certain point after 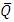 exceeds one.b. The frictional force increases with the Brownian motion number
exceeds one.b. The frictional force increases with the Brownian motion number 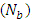 , whereas decreases with the thermophoresis parameter
, whereas decreases with the thermophoresis parameter 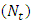 and inclination
and inclination  . Frictional force decreases with wave amplitude
. Frictional force decreases with wave amplitude 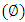 and increases with wave length
and increases with wave length 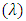 but converges to a particular value after
but converges to a particular value after 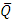 is one.c. The frictional force has a similar behaviour compared to the pressure drop.d. The temperature profile decreases with the Brownian motion number
is one.c. The frictional force has a similar behaviour compared to the pressure drop.d. The temperature profile decreases with the Brownian motion number 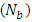 and increases with the thermophoresis parameter
and increases with the thermophoresis parameter 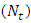 .e. The nanoparticle phenomena increases with the Brownian motion number
.e. The nanoparticle phenomena increases with the Brownian motion number 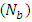 and decreases with the thermophoresis parameter
and decreases with the thermophoresis parameter 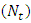 .f. The temperature profile has an opposite behaviour compared to nanoparticle phenomena.g. For sinusoidal, triangular and trapezoidal waves, maximum pressure gradient occurred for
.f. The temperature profile has an opposite behaviour compared to nanoparticle phenomena.g. For sinusoidal, triangular and trapezoidal waves, maximum pressure gradient occurred for 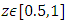 with increase in wave amplitude. For square wave, it is for
with increase in wave amplitude. For square wave, it is for  and multi sinusoidal wave it is for
and multi sinusoidal wave it is for 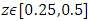 .h. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
.h. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
ACKNOWLEDGEMENTS
The authors wish to thank the referees for their valuable and constructive comments which lead to significant improvement of the paper.
References
| [1] | Buongiorno J, Convective transport in nanofluids, ASME J Heat Transf. 128 (2006) 240-250. |
| [2] | Choi SUS, Enhancing thermal conductivity of fluids with nanoparticles, In: Siginer DA, Wang HP (eds) Developments and applications of Non-Newtonian flows, ASME, New York, 66 (1995) 99-105. |
| [3] | Das SK, Putra N, Roetzel W, Pool boiling of nano-fluids on horizontal narrow tubes, Int. J Multiph. Flow 29 (2003) 1237-1247. |
| [4] | Devi RG, Devanathan R, Peristaltic motion of a micro polar fluid, Proc. Indian Acad. Sci.81A (1975) 149-163. |
| [5] | Fung YC, Yih CS, Peristaltic transport, J. Appl. Mech. Trans. ASME 5 (1968) 669-675. |
| [6] | He JH, Application of homotopy perturbation method to nonlinear wave equations, Chaos Solitons Fractals 26 (2005) 695-700. |
| [7] | He JH, Approximate analytical solution for seepage flow with fractional derivatives in porous media, Comput. Methods Appl. Mech. Eng. 167 (1998) 57-68. |
| [8] | He JH, Homotopy perturbation technique, Comput. Methods Appl. Mech. Eng. 178 (1999) 257-262. |
| [9] | Khan WA, Pop I, Boundary-layer flow of a nanofluid past a stretching sheet, Int. J Heat Mass Transfer 53 (2010) 2477-2483. |
| [10] | Kuznetsov AV, Nield DA, Natural Convective boundary layer flow of a nanofluid past a vertical plate, Int. J Thermo Sci. 49 (2010) 243-247. |
| [11] | Latham TW, Fluid motion in a peristaltic pump, MS. Thesis, Massachusetts Institute of Technology, Cambridge (1996). |
| [12] | Maruthi Prasad K, Radhakrishnamacharya G, Flow of Herschel – Bulkley Fluid in an inclined tube of Non-Uniform Cross-Section with Multiple Stenoses, Arch. Mech. 60(2) (2008) 159-170. |
| [13] | Maruthi Prasad K, Radhakrishnamacharya G, J V Ramana Murthy, Peristaltic pumping of a micropolar fluid in an inclined tube, Int. journal of Appl. Math and Mech. 6(11) (2010) 26-40. |
| [14] | Maruthi Prasad K, Ramana Murthy JV, VK Narla, Unsteady Peristaltic Transport in Curved Channels, Physics of Fluids, 25 (2013) 091903, DOI:10.1063/1.4821355. |
| [15] | Mekheimer Kh S, Peristaltic Flow of Blood under Effect of a Magnetic Field in a Non-Uniform Channels, Appl. Math. Comput.153 (2004) 763-767. |
| [16] | Misra M, Rao AR, Peristaltic Transport of a Newtonian Fluid in an Asymmetric Channel, ZAMM 54 (2003) 532-550. |
| [17] | Muthu P, Ratish Kumar BV, Chandra P, On the influence of wall properties in the peristaltic motion of micro polar fluid, ANZIAM J. 45 (2003) 245-260. |
| [18] | Noreen Sher Akbar, Nadeem S, T Hayat, Awatif a. Hendi, Peristaltic flow of a nanofluid in a non-uniform tube, Heat and Mass Transfer 48 (2011) 451-459. |
| [19] | Radhakrishnamacharya G, Srinivasulu Ch, Influence of Wall Properties on Peristaltic Transport with heat transfer, Comptes Rendus Mechanique 335 (2007) 460-480. |
| [20] | Shapiro AH, Jaffrin MY, Weinberg SL, Peristaltic pumping with long wavelengths at low Reynolds numbers, J. Fluid Mech. 37 (1969) 799-825. |
| [21] | Srivastava LM, Srivastava VP, Peristaltic Transport of Blood: Casson Model II, J. Biomech. Eng. 104 (1982) 182-189. |

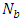 but decreases with the thermophoresis number
but decreases with the thermophoresis number 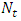 and inclination
and inclination 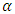 . It is also found that the pressure drop decreases with wave amplitude and increases with wave length. The frictional force increases with Brownian motion parameter
. It is also found that the pressure drop decreases with wave amplitude and increases with wave length. The frictional force increases with Brownian motion parameter 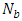 , wavelengthand decreases with the thermophoresis number
, wavelengthand decreases with the thermophoresis number 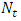 , inclination
, inclination 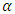 and wave amplitude. It can be seen that, thattemperature profile decreases with the Brownian motion parameter
and wave amplitude. It can be seen that, thattemperature profile decreases with the Brownian motion parameter 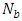 and increases with the thermophoresis number
and increases with the thermophoresis number 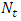 . Thenanoparticle phenomena increases with the Brownian motion parameter
. Thenanoparticle phenomena increases with the Brownian motion parameter 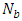 and decreases with the thermophoresis number
and decreases with the thermophoresis number 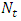 . It is observed that, the maximum pressure gradient occurs for different values of wave amplitude for sinusoidal, multi sinusoidal, triangular, trapezoidal and square waves. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
. It is observed that, the maximum pressure gradient occurs for different values of wave amplitude for sinusoidal, multi sinusoidal, triangular, trapezoidal and square waves. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
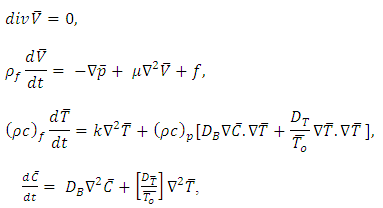 where
where 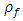 is the density of the fluid,
is the density of the fluid, 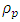 is the density of the particle,
is the density of the particle, 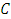 is the volumetric volume expansion coefficient,
is the volumetric volume expansion coefficient, 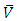 is the velocity vector,
is the velocity vector, 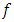 is the body forces,
is the body forces, 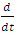 represents the material time derivative ,
represents the material time derivative , 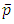 is the pressure,
is the pressure, 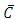 is the nanoparticle phenomena,
is the nanoparticle phenomena, 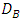 is the Brownian diffusion coefficient and
is the Brownian diffusion coefficient and 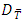 is the thermophoretic diffusion coefficient. The ambient values of
is the thermophoretic diffusion coefficient. The ambient values of 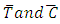 as
as 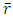 tend to
tend to 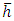 are denoted by
are denoted by 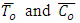 .
.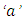 with sinusoidal waves travelling along the tube with speed
with sinusoidal waves travelling along the tube with speed 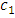 , amplitude
, amplitude 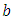 and wave length
and wave length 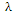 . Further suppose the tube is inclined at an angle
. Further suppose the tube is inclined at an angle 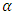 with the horizontal axis as shown in Figure 1. Heat transfer and nano-particle phenomena are considered. At the center of the tube, symmetry condition is used on both temperature and concentration, while the walls of the tube maintain temperature
with the horizontal axis as shown in Figure 1. Heat transfer and nano-particle phenomena are considered. At the center of the tube, symmetry condition is used on both temperature and concentration, while the walls of the tube maintain temperature 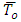 and nanoparticle volume fraction
and nanoparticle volume fraction 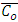 .
.
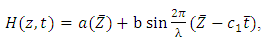
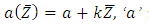 is the radius of the inlet,
is the radius of the inlet, 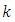 is the constant whose magnitude depends on the length of the tube and
is the constant whose magnitude depends on the length of the tube and 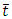 is the time. Cylindrical coordinate system
is the time. Cylindrical coordinate system 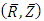 is chosen, so that
is chosen, so that 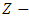 axis coincides with the center line of the tube and
axis coincides with the center line of the tube and 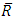 is transverse to it. Further, the flow is assumed to be axisymmetric.Using the transformations
is transverse to it. Further, the flow is assumed to be axisymmetric.Using the transformations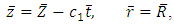
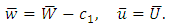
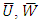 and
and 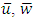 are velocity components in the radial and axial directions in the fixed and moving frames respectively, the governing equations in a fixed frame for an incompressible nanofluid in an inclined tube are given by
are velocity components in the radial and axial directions in the fixed and moving frames respectively, the governing equations in a fixed frame for an incompressible nanofluid in an inclined tube are given by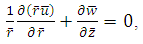
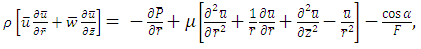
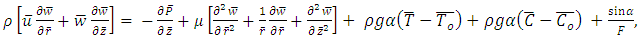
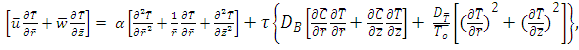
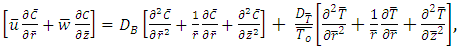
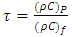 is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid.The boundary conditions in the wave frame are as follows
is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid.The boundary conditions in the wave frame are as follows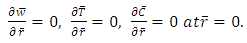
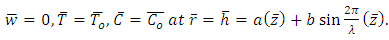
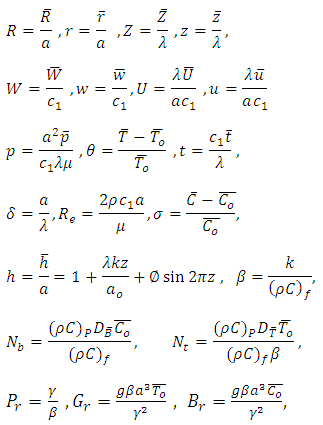
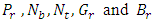 are the Prandtl number, the Brownian motion parameter, the thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number.Introducing the non-dimensional variables into equations (4)-(10) under the assumption of long wave length and low Reynolds number approximations, the equations (4)-(10) reduces to
are the Prandtl number, the Brownian motion parameter, the thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number.Introducing the non-dimensional variables into equations (4)-(10) under the assumption of long wave length and low Reynolds number approximations, the equations (4)-(10) reduces to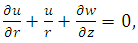
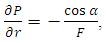
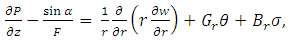
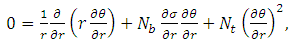
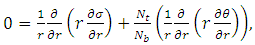
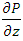 is a function of z only.The non-dimensional boundary conditions are
is a function of z only.The non-dimensional boundary conditions are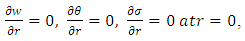
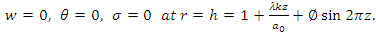
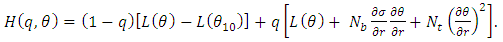
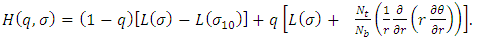
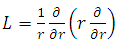 is taken as linear operator.
is taken as linear operator.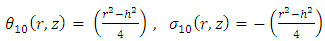
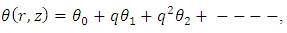
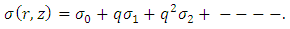
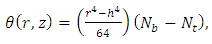
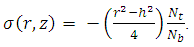
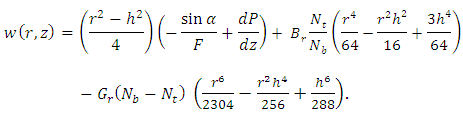
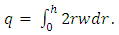
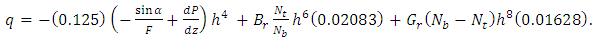
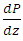 can be written as
can be written as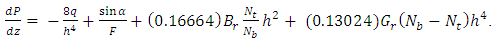
 is defined by
is defined by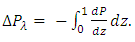
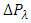 can be written as
can be written as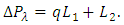
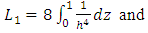
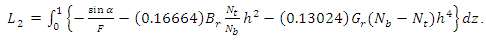
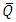 is given by
is given by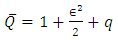
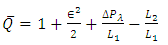
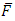 at the wall is given by
at the wall is given by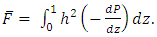
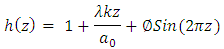 2. Multi Sinusoidal Wave:
2. Multi Sinusoidal Wave: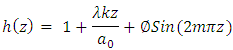 3. Triangular Wave:
3. Triangular Wave: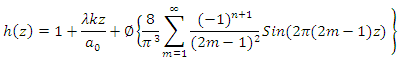 4. Trapezoidal Wave:
4. Trapezoidal Wave: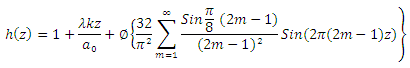 5. Square Wave:
5. Square Wave: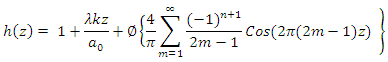
 , time averaged flux
, time averaged flux 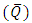 and frictional forces
and frictional forces 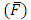 are given by the equations (23), (34) and (35) respectively. The effects of various parameters on pressure drop
are given by the equations (23), (34) and (35) respectively. The effects of various parameters on pressure drop 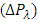 , time averaged flux
, time averaged flux 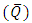 , frictional force
, frictional force 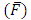 , temperature profile and nanoparticle phenomena have been calculated numerically by using Mathematica 9.0 software and the results are graphically presented in figures 2(a)-5(b). The pressure gradient for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves has been graphically represented from figures 6(a)-6(e). Stream lines for sinusoidal and multi sinusoidal waves are represented from figures 7(a)-7(b).The effects of various parameters on the pressure drop
, temperature profile and nanoparticle phenomena have been calculated numerically by using Mathematica 9.0 software and the results are graphically presented in figures 2(a)-5(b). The pressure gradient for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves has been graphically represented from figures 6(a)-6(e). Stream lines for sinusoidal and multi sinusoidal waves are represented from figures 7(a)-7(b).The effects of various parameters on the pressure drop 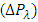 are shown in figures 2(a)-2(e), for various values of Brownian motion number
are shown in figures 2(a)-2(e), for various values of Brownian motion number 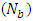 , thermophoresis parameter
, thermophoresis parameter 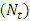 , inclination
, inclination 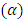 , wave length
, wave length  and wave amplitude
and wave amplitude 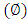 . It is observed that pressure drop increases with Brownian motion number
. It is observed that pressure drop increases with Brownian motion number 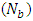 but decreases with thermophoresis parameter
but decreases with thermophoresis parameter 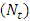 and inclination
and inclination 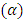 . Pressure drop
. Pressure drop 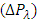 decreases with wave amplitude
decreases with wave amplitude  and increases with wave length
and increases with wave length 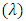 but it is interesting to note that the pressure drop converges to a particular value when the value of
but it is interesting to note that the pressure drop converges to a particular value when the value of 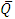 exceeds 1.Figures 3(a)-3(e) represent the behaviour of frictional force
exceeds 1.Figures 3(a)-3(e) represent the behaviour of frictional force 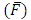 for different values of Brownian motion number
for different values of Brownian motion number 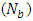 , thermophoresis parameter
, thermophoresis parameter 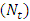 , inclination
, inclination 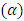 , wave length
, wave length 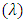 and wave amplitude
and wave amplitude 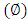 . It is observed that frictional force increases with the Brownian motion number
. It is observed that frictional force increases with the Brownian motion number 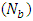 but decreases with the thermophoresis parameter
but decreases with the thermophoresis parameter 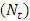 and inclination
and inclination 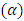 . Frictional force
. Frictional force 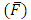 decreases with wave amplitude
decreases with wave amplitude 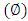 and increases with wave length
and increases with wave length 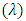 but converges to a particular value when
but converges to a particular value when 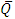 exceeds 1.It can be seen from figures 4(a)-4(b) that, temperatureprofile
exceeds 1.It can be seen from figures 4(a)-4(b) that, temperatureprofile 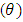 decreases with the Brownian motion parameter
decreases with the Brownian motion parameter 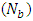 whereas increases with the thermophoresis parameter
whereas increases with the thermophoresis parameter 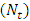 .Nanoparticle phenomena
.Nanoparticle phenomena 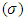 has been shown from figures 5(a)-5(b) for different values of Brownian motion number
has been shown from figures 5(a)-5(b) for different values of Brownian motion number 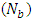 and thermophoresis parameter
and thermophoresis parameter 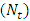 . It is observed that nanoparticle phenomena increases with the Brownian motion parameter
. It is observed that nanoparticle phenomena increases with the Brownian motion parameter 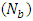 but decreases with the thermophoresis parameter
but decreases with the thermophoresis parameter 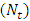 . From the graphs it is interested to note that the temperature profile has an opposite behaviour as compared to the nanoparticle phenomena.Pressure gradient
. From the graphs it is interested to note that the temperature profile has an opposite behaviour as compared to the nanoparticle phenomena.Pressure gradient 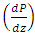 has been presented from figures 6(a)-6(e) for different values of wave amplitude
has been presented from figures 6(a)-6(e) for different values of wave amplitude 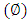 for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves. Maximum pressure gradient occurs in sinusoidal wave, triangular wave and trapezoidal waves for
for sinusoidal wave, multi sinusoidal wave, triangular wave, trapezoidal wave and square waves. Maximum pressure gradient occurs in sinusoidal wave, triangular wave and trapezoidal waves for 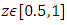 but interestingly for square wave pressure gradient
but interestingly for square wave pressure gradient 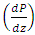 is maximum for
is maximum for 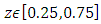 whereas for multi sinusoidal wave, the pressure gradient
whereas for multi sinusoidal wave, the pressure gradient 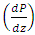 is maximum for
is maximum for 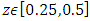 .Figures 7(a)-7(b) shows streamlines for sinusoidal and multi sinusoidal waves. It is noticed that the size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
.Figures 7(a)-7(b) shows streamlines for sinusoidal and multi sinusoidal waves. It is noticed that the size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.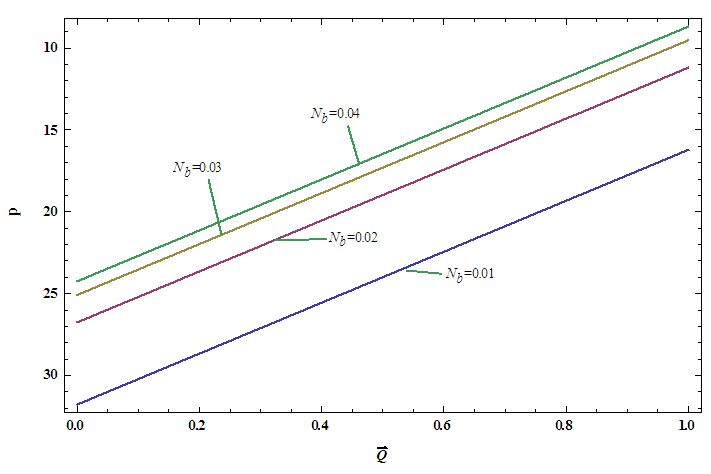
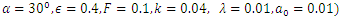
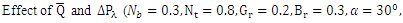
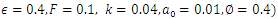
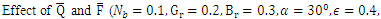
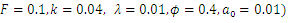
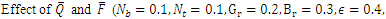
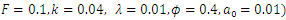
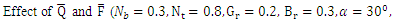
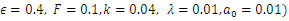


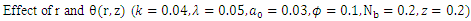

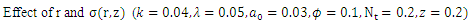

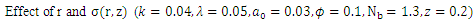

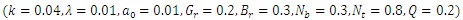

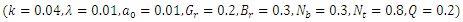

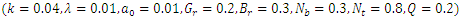

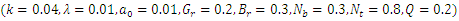

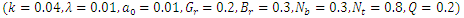

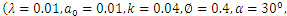
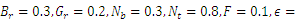
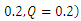

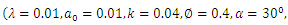
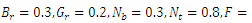
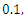
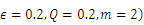
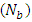 , whereas decreases with the thermophoresis parameter
, whereas decreases with the thermophoresis parameter 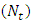 and inclination
and inclination 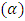 . Pressure drop decreases with wave amplitude
. Pressure drop decreases with wave amplitude 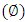 and increases with wave length
and increases with wave length 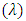 but converges to a certain point after
but converges to a certain point after 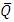 exceeds one.b. The frictional force increases with the Brownian motion number
exceeds one.b. The frictional force increases with the Brownian motion number 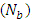 , whereas decreases with the thermophoresis parameter
, whereas decreases with the thermophoresis parameter 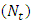 and inclination
and inclination  . Frictional force decreases with wave amplitude
. Frictional force decreases with wave amplitude 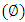 and increases with wave length
and increases with wave length 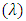 but converges to a particular value after
but converges to a particular value after 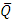 is one.c. The frictional force has a similar behaviour compared to the pressure drop.d. The temperature profile decreases with the Brownian motion number
is one.c. The frictional force has a similar behaviour compared to the pressure drop.d. The temperature profile decreases with the Brownian motion number 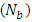 and increases with the thermophoresis parameter
and increases with the thermophoresis parameter 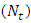 .e. The nanoparticle phenomena increases with the Brownian motion number
.e. The nanoparticle phenomena increases with the Brownian motion number 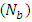 and decreases with the thermophoresis parameter
and decreases with the thermophoresis parameter 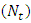 .f. The temperature profile has an opposite behaviour compared to nanoparticle phenomena.g. For sinusoidal, triangular and trapezoidal waves, maximum pressure gradient occurred for
.f. The temperature profile has an opposite behaviour compared to nanoparticle phenomena.g. For sinusoidal, triangular and trapezoidal waves, maximum pressure gradient occurred for 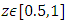 with increase in wave amplitude. For square wave, it is for
with increase in wave amplitude. For square wave, it is for  and multi sinusoidal wave it is for
and multi sinusoidal wave it is for 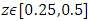 .h. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.
.h. The size of the trapped bolus in multi sinusoidal wave is small as compared to the sinusoidal wave.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML