1. Introduction

The fuzzy sets theory was created by Zadeh in 1965 [16] in response to have a mathematical representation of situations in which definitions have not clear boundaries (e.g. the “high mountains” of a country, the “good players” of a football team, etc). For general facts on fuzzy sets we refer to the book [5].

Fuzzy logic, the development of which is based on fuzzy sets theory [17], provides a rich and meaningful addition to standard Boolean logic. Unlike Boolean logic, which has only two states, true or false, fuzzy logic deals with truth values which range continuously from 0 to 1. Thus something could be half true 0.5 or very likely true 0.9 or probably not true 0.1, etc. In this way fuzzy logic allows one to express knowledge in a rule format that is close to a natural language expression and therefore it opens the door to construction of mathematical solutions of computational problems which are inherently imprecisely defined.

The assessment of a system’s effectiveness (i.e. of the degree of attainment of its targets) with respect to an action performed within the system (e.g. problem-solving, decision making, learning performance, etc) is a very important task that enables the correction of the system’s weaknesses resulting to the improvement of its general performance. The assessment methods that are commonly used in practice are based on the principles of the classical, bivalent logic (yes-no). However, there are cases where a crisp characterization is not probably the proper one for an assessment. For example, a teacher is frequently not sure about a particular numerical grade characterizing a student’s performance.

Fuzzy logic, due to its nature of characterizing a case with multiple values, offers wider and richer resources covering such kind of cases. This gave as several times in the past the impulse to apply principles of fuzzy logic for the assessment of human or machine (in case of CBR systems) skills using as tools the corresponding system’s total uncertainty (e.g. see [11] and its relevant references, [14], etc), the Center of Gravity (COG) defuzzification technique (e.g. see [6, 14], etc) as well as the recently developed variations of this technique of the Triangular (e.g. see [7, 8], etc) and of the Trapezoidal (e.g. see [9, 13, 14], etc) Fuzzy Assessment Models (or, for brevity. TFAM and TRFAM respectively). The above fuzzy methods, although they can be used for individual assessment as well [12], they are more appropriate for accessing the overall performance of a group of individuals (or objects) sharing common characteristics (e.g. students, players, CBR systems, etc). For some more details about these methods see also Section 4.

In the present paper we shall use the Trapezoidal Fuzzy Numbers (TpFNs) for assessing human skills. In contrast to the above mentioned fuzzy assessment methods, this approach is more appropriate for individual assessment. However, we shall adapt it for use as a tool for group assessment too.

The rest of the paper is organized as follows: In Section 2 we present the notion of Fuzzy Number (FN), while in Section 3 we present the TpFNs and the arithmetic operations of addition and subtraction defined among them. In Section 4 we describe how one can use the TpFNs for assessing human skills and we discuss the advantages and disadvantages of this method with respect to the alternative fuzzy assessment methods applied in earlier papers (see above) Finally, Section 5 is devoted to our conclusion and a brief discussion for the perspectives of future research on the subject.

2. Fuzzy Numbers

A Fuzzy Number (FN) is a special form of fuzzy set on the set R of real numbers. FNs play a fundamental role in fuzzy mathematics, analogous to the role played by the ordinary numbers in classical mathematics. For general facts on FNs we refer to Chapter 3 of the book [10], which is written in Greek language, and also to the books [3, 4].

For a better understanding of the notion of a FN (by those not familiar to it) we shall start with the following three introductory definitions:

Definition 1: A fuzzy set A on U with membership function y=m(x) is said to be normal, if there exists x in U, such that m(x) = 1.

Definition 2: Let A be as in definition 2, and let x be a real number of the interval [0, 1]. Then the x-cut of A, denoted by A^x, is defined to be the crisp set

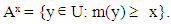Definition 3: A fuzzy set A on R is said to be convex, if its x-cuts A^x are ordinary closed real intervals, for all x in [0, 1].

For example, for the fuzzy set A whose membership function’s graph is represented in Figure 1, we observe that A^0.4 = [5, 8.5] 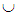[11, 13] and therefore A is not a convex fuzzy set.

Figure 1. Graph of a non convex fuzzy set

We are ready now to give the definition of a FN:

Definition 4: A fuzzy number is a normal and convex fuzzy set A on R with a piecewise continuous membership function.

Figure 2 represents the graph of a FN expressing the fuzzy concept: “The real number x is approximately equal to 5”. We observe that the membership function of this FN takes constantly the value 0 outside the interval [0, 10], while its graph in [0, 10] is a parabola.

Figure 2. Graph of a fuzzy number

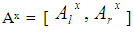Since the x-cuts A^x of a FN A are closed real intervals, we can write for each x in [0, 1], where 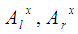are real numbers depending on x.

The following statement defines a partial order in the set of all FNs:

Definition 5: Given the FNs A and B we write 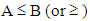if, and only if, 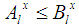and 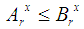for all x in [0, 1]. Two FNs for which the above relation holds are called comparable, otherwise they are called non comparable.

3. Trapezoidal Fuzzy Numbers (TpFNs)

3.1. Triangular Fuzzy Numbers (TFNs)

The simplest form of a FN is probably the Triangular Fuzzy Number (TFN). The definition of a TFN is given as follows:

Definition 6: Let a, b and c be real numbers with a < b < c. Then the Triangular Fuzzy Number (TFN) A = (a, b, c) is the FN with membership function:

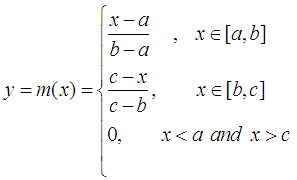Obviously we have that m(b)=1, while b need not be in the “middle” of a and c.

For example, let us consider the FN, say A, of Figure 3 representing the same fuzzy concept with the FN of Figure 2. We observe that the membership function y=m(x) of A takes constantly the value 0, if x is outside the interval [0, 10], while its graph in the interval [0, 10] is the union of two straight line segments forming a triangle with the OX axis. More explicitly, we have 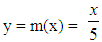, if x is in [0, 5], and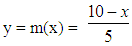, if x is in [5, 10]. This is a typical example of a TFN and we can write

A= (0, 5, 10).

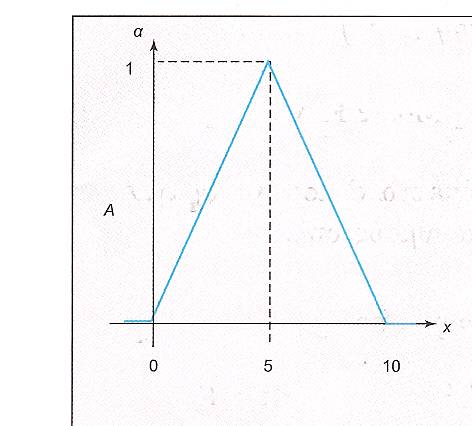Figure 3. Graph of the TFN (0, 5, 10)

In the paper [15] written just before the present one we have used the TFNs as a tool for assessing student skills. For this, starting with the traditional methods of the bivalent logic, we firstly assigned to each student a numerical score from 0 to 100 representing his (her) progress.

Then, we considered the set U = {A, B, C, D, F} of linguistic labels (grades) corresponding to the above scores as follows: A (85-100) = excellent, B (84-75) = very good, C (74-60) = good, D (59-50) = fair and F (<50) = unsatisfactory.

It is easy to verify that the above linguistic labels can be replaced by TFNs (denoted for reasons of simplicity) by the same letters) as follows: A= (85, 92.5, 100), B = (75, 79.5, 84), C = (60, 67, 74), D= (50, 54.5, 59) and F = (0, 24.5, 49). The process followed for this replacement is quite obvious. Namely, the middle entry of each TFN is equal to the mean value of the student scores previously attached to the corresponding linguist label (grade).

In this way a TFN corresponds to each student assessing his (her) individual performance. Further, in [15] we have extended this method for assessing the overall performance of student groups, by introducing the mean value of a finite set of TFNs (see Definition 8 in [15]). In this way one takes a general idea about the performance of a given group, but it is not always possible to compare the performances of two different groups. This is due to the fact that two TFNs are not always comparable (see Definition 5).

In concluding, TFNs can be used, when one wants to assess the possibility of a value to be in a given closed interval; e.g. the grade excellent for a student, being in the interval of scores [85, 100].

However, they are also cases in practice, in which one wants to assess the possibility of a closed interval of values to be in another (prefixed) closed interval. This assessment can be performed using as a tool the TpFNs (see example of Section 4.3). The notion of a TpFN and basic arithmetic operations between TpFNs are presented in the next subsection.

3.2. The Notion of TpFNs and Basic Arithmetic Operations on them

The TpFN (a₁, a₂, a₃, a₄) is geometrically represented in Figure 4, where a₁< a₂<a₃< a₄ are given real numbers.

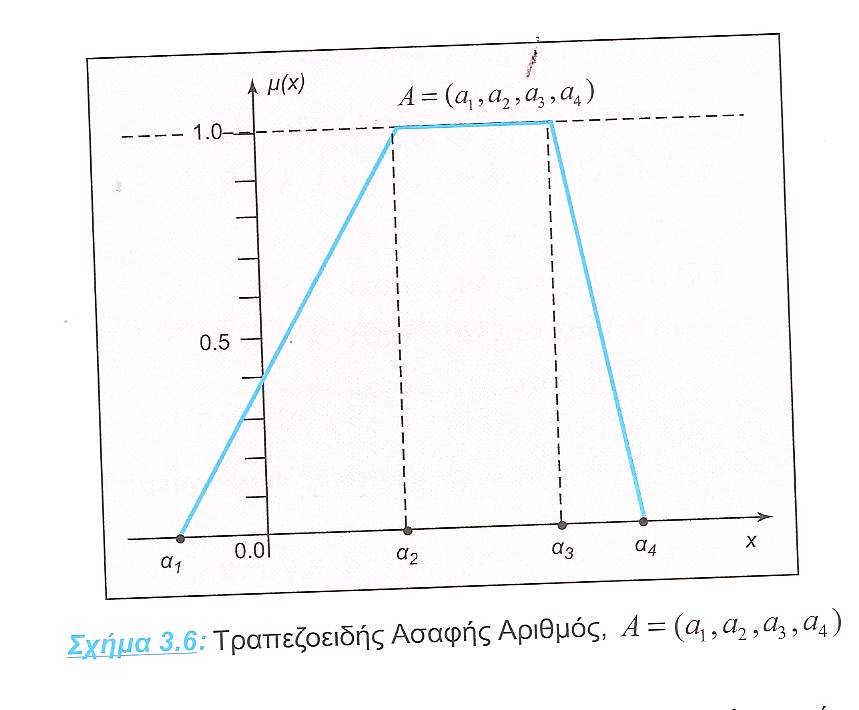Figure 4. Graph of the TpFN (a1, a2, a3, a4)

We observe that its membership function y=m(x) is constantly 0 outside the interval [a₁, a₄], while its graph in this interval is the union of three straight line segments forming a trapezoid with the 0X axis. Therefore, its analytic definition can be given as follows:

Definition 7: Let a₁< a₂<a₃< a₄ be given real numbers. Then the TpFN (a₁, a₂, a₃, a₄) is the FN with membership function:

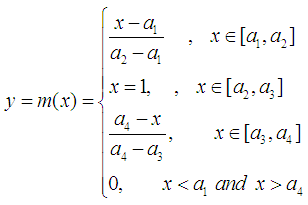The basic arithmetic operations between FNs can be performed in general in two alternative ways:

i) With the help of their x-cuts, which, as we have already seen, are ordinary closed intervals of R. For this, if A and B are given TFNs, then an arithmetic operation * between them is defined by 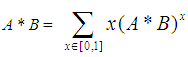, where (A*B)^x = A^x * B^x (for reasons of simplicity * in the second term of the last equation symbolizes the corresponding operation defined on the closed real intervals). Therefore, according to this approach, the Fuzzy Arithmetic is actually based on the arithmetic of the real intervals.

ii) By applying the Zadeh’s extension principle (see Section 1.4, p.20 of [5]), which provides the means for any function f mapping the crisp set X to the crisp set Y to be generalized so that to map fuzzy subsets of X to fuzzy subsets of Y.

In practice the above two general methods of the fuzzy arithmetic, requiring laborious calculations, are rarely used in applications, where the utilization of simpler forms of FNs is preferred, including the TFNs and TpFNs.

It can be shown that the above two general methods lead to the following simple rules for the addition and subtraction of TpFNs:

Let A = (a₁, a₂, a₃, a₄) and B = (b₁, b₂, b₃, b₄) be two TFNs. Then

• The sum A + B = (a₁+b₁, a₂+b₂, a₃+b₃, a₄+b₄).

• The difference A - B = A + (-B) = (a₁-b₄, a₂-b₃, a₃-b₂, a₄-b₁), where

–B = (-b_4, -b₃, -b₂, -b₁) is defined to be the opposite of B.

In other words, the opposite of a TpFN, as well as the sum and the difference of two TpFNs are also TpFNs.

On the contrary, the product and the quotient of two TFNs, although they are FNs, they are not always TpFNs, apart from some special cases, or in terms of suitable approximating formulas (for more details see [3]).

Further, one can define the following two scalar operations:

• k + A= (k+a₁, k+a₂, k+a₃, k+a₄), k∈R

• kA = (ka₁, ka₂, ka₃, ka₄), if k>0 and kA = (ka₄, ka₃, ka₂, ka₁), if k<0.

We close this section with the following definition, which will be used in the next section for assessing the overall performance of a set of similar objects (e.g. humans) with the help of TpFNs:

Definition 8: Let A_i = (a_1i, a_2i, a_3i, a_4i), i = 1, 2, …, n be TpFNs, where n is a non negative integer, n≥2. Then we define the mean value of the above TpFNs to be the TpFN: .

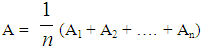4. Use of the TpFNs for Assessing Human Skills

In this section we shall use the TpFNs as an alternative tool for assessing human skills. For this, we consider the following example:

EXAMPLE: The performance of the five players of a basket-ball team who started a game was individually assessed by six different athletic journalists using a scale from 0 to 100 as follows:

P₁ (player 1): 43, 48, 49, 49, 50, 52, P₂: 81, 83. 85, 88, 91, 95, P₃: 76, 82, 89, 95, 95, 98, P₄: 86, 86, 87, 87, 87, 88 and P₅: 35, 40, 44, 52, 59, 62.

The players’ performance is characterized by the fuzzy linguistic labels A, B, C, D and F introduced in Section 3.1. How one can assess their individual and overall performance in this particular game?

4.1. Summary of Our Previous Research (for Details See [14, 15])

We shall start with two traditional assessment methods connected to the principles of the classical (bivalent) logic:

In fact, calculating the mean values of the above scores for each player, one approximately finds the following individual mean performances for them (in parentheses we give the corresponding qualitative characterizations): P₁: 48.5 (F), P₂: 87.17 (A), P₃: 89.17 (A), P₄: 86.83 (A) and P₅: 48.67(F). Also, calculating the mean value of the above individual means on finds that their overall mean performance is approximately equal to 72.05, i.e. it can be characterized as very good (B).

Further, observing the players’ scores (n=5.6=30 in total scores) one finds that 14 of them are characterized as excellent (A), 4 as very good (B), 1 as good (C), 4 as fair (D) and 7 are characterized as unsatisfactory. Then, the Grade Point Average (GPA) index is calculated by the formula 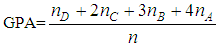(1) (e.g. cf. [1]), where n_x denotes the number of scores which correspond to the linguistic label x in U. From formula (1) it is easy to verify that the worst value of GPA is 0 (when n_F = n and n_A = n_B = n_C = n_{D =} 0) and its maximal value is 4 (when n_A = n and n_B = n_C = n_{D =} n_F = 0). Applying formula (1) on the data of our experiment one finds approximately the value GPA = 2.47. The value of GPA, characterizes the players’ overall quality performance, because in formula (1) higher coefficients are attached to the higher scores. Thus, since the value 2.47 is greater than the half of the maximal GPA’s value (4:2=2), the basket-ball players’ overall performance is characterized more than satisfactory.

In an Example, presented in [14], we have applied three different fuzzy methods for student assessment: First, expressing the two student departments D₁ and D₂ of this Example as fuzzy sets in U (the membership function was defined by 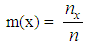for each department), we calculated the total (possibilistic) uncertainty in each case and we found the values 0.259 for D₁ and 0.934 for D₂ respectively. This shows that D₁ demonstrated a considerably better (mean) performance than D₂. Further, the application of the COG defuzzification technique, as well as of the TRFAM showed that (in contrast to the mean performance) D₂ demonstrated a slightly better quality performance than D₁.

Also in [14], the differences appeared in the results obtained by applying the above (five in total) traditional and fuzzy assessment methods, were adequately explained and justified through the nature of each method. This provided a very strong indication for the creditability of the above three innovative fuzzy assessment methods.

Finally, as it already has been stated in Section 3.1, in the very recent article [15] we have used the TFNs as an alternative tool for the student assessment (by reconsidering the above mentioned Example of [14]).

4.2. Use of the TpFNs for Assessing the Individual Players’ Performance

Let us now come to the main target of this paper, which is the use of TpFNs as an. alternative tool for assessing human skills. For this, in the Example presented above we assign to each basket-ball player P_i a TpFN (denoted, for simplicity, by the same letter) as follows: P₁ = (0, 43, 52, 59), P₂ = (75, 81, 95, 100), P₃ = (75, 76, 98, 100), P₄ = (85, 86, 88, 100) and P₅ = (0, 35, 62, 74).

Each of the above TpFNs characterizes the individual performance of the corresponding player in the form (a₁, a₂, a₃, a₄), where a₁ is the lower bound of his performance with respect of the linguistic labels of the set U (see Section 3.1), a₂ and a₃ are the lower and higher scores respectively assigned to the corresponding player by the athletic journalists and a₄ is the upper bound of his performance with respect to U.

Alternatively, for the players’ individual assessment, instead of TpFNs one could use TFNs of the form (a, b, c), where a is the lower bound of his individual mean performance with respect to U, b is his mean performance (calculated in the beginning of Section 4.1) and c is the upper bound of his mean performance with respect to U. Therefore, we can write P₁ = (0, 48.5, 49), P₂ = (85, 87.17, 100), P₃ = (85, 89.17, 100), P₄ = (85, 86.83, 100) and P₅ = (0, 48.67, 49) (see also Example of [14]).

Notice that in [12], as an alternative individual student assessment method, an ordered triple of fuzzy linguistic labels was assigned to each student. It was shown also in [12] that this approach is equivalent with the A. Jones method [2] of assessing a student’s knowledge in terms of his (her) fuzzy deviation with respect to the teacher. However, the method with the TpFNs (or TFNs) presented here is more comprehensive, since it treats the (fuzzy) individual student assessment numerically.

4.3. Use of the TpFNs for Assessing the Overall Players’ Performance

Next, we are going to adapt the individual assessment method presented in Section 4.2 in order to be used in our Example for assessing the overall players’ performance in terms of the TpFNs. For this, we simply calculate the mean value of the TpFNs P_i , i =1, 2, 3, 4, 5 (see Definition 8), which is equal to

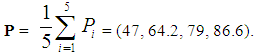The above value of P gives us the following information:

(i) The players’ performance, according to the scores assigned to them by the athletic journalists, was fluctuated from unsatisfactory (a₁=47) to excellent (a₄=86.6).

(ii) The overall players’ mean performance is lying in the interval [a₂, a₃] = [64.2, 79], i.e. it can be characterized from good (C) to very good (B).

However, the above method (of the mean value of the TpFNs) is not always appropriate to be used when one wants to compare the overall performance of two (or more} groups of players, because two (or more) TpFNs are not always comparable (see Definition 5). This is the main disadvantage of this assessment method with respect to the other assessment methods reported in Section 4.1.

Finally, notice that the same method can be used by utilizing TFNs instead of TpFNs to represent the players’ performance (see Section 4.2). In this case the mean value of the corresponding TFNs is equal to 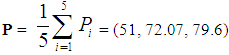¹, which shows that the players’ overall performance lies in the interval [51, 79.6] (fair to very good), while their overall mean performance (72.07) is characterized as good.

5. Conclusions

In the present paper we used the TpFNs as a tool for assessing human skills. The main advantage of this approach is that in case of individual assessment leads to a numerical result, which is more comprehensive than the qualitative results obtained in earlier works by applying alternative fuzzy assessment methods. On the contrary, in case of group assessment this method leads only to a linguistic characterization of the corresponding group’s overall performance and it is not always sufficient for comparing the performances of two different groups, as our fuzzy assessment methods applied in earlier works do. This is due to the fact that the inequality between FNs defines on them a relation of partial order only and therefore two TpFNs are not always comparable.

Our method of using the TpFNs (or TFNs) for human assessment is of general character and therefore it could be utilized in future for assessing other human (or machine) activities too. Further, the effort of finding an alternative method for comparing the overall performance of different groups using the TpFNs (TFNs) is of a particular interest. For example, a defuzzification technique could be used for this purpose. All the above will be our targets for future research on the subject.

Note

1. The addition of TFNs and the scalar multiplication of a TFN with a real number are defined in the same way as for TpFNs (see Section 3.2 and [14]) and Definition 8 holds for TFNs too (see [14])