M. R. Odekunle1, M. O. Egwurube1, K. A. Joshua2
1Department of Mathematics, Modibbo Adama University of Technology, Yola, Nigeria
2Department of Mathematics, Adamawa state University, Mubi, Nigeria
Correspondence to: K. A. Joshua, Department of Mathematics, Adamawa state University, Mubi, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
First order one-stage explicit Stochastic Rational Runge-Kutta methods were derived for the solution of stochastic ordinary differential equations. The derivation is based on the use of Taylor series expansion for both the deterministic and stochastic parts of the stochastic differential equation. The stability and convergence of the methods, found to be absolute stable. These methods were further tested on some numerical problems. From the results obtained, it is obvious that the derived methods; performed better than the ones with which we have analysed and they were compared with our results.
Keywords:
Stochastic differential equations, Runge-Kutta methods, Explicit rational Runge-Kutta methods
Cite this paper: M. R. Odekunle, M. O. Egwurube, K. A. Joshua, Solution of Stochastic Ordinary Differential Equations Using Explicit Stochastic Rational Runge-Kutta Schemes, American Journal of Computational and Applied Mathematics , Vol. 5 No. 4, 2015, pp. 105-110. doi: 10.5923/j.ajcam.20150504.02.
1. Introduction
Development in recent years in area of researches globally, in Mathematics and science related subjects such as, Engineering, Physics, Biology, Ecology, Hydrology, Economics, Investment, Finance, and population dynamics, just to mention but a few, have realised the importance of application of stochastic differential equations and the importance of random effects in most real problems. These are difficult to handle by the deterministic models [1, 2]. In view of this, there have been an increase in the need to construct stochastic models to simulate systems that deal with real life situations that contain uncertainties. Many physical systems are modelled by stochastic differential equations where random effects (noise) are being modelled by a Brownian motion or what is called Wiener process [3]. Such differential equations are rarely solved analytically due to diffusion term involved. So numerical methods required and should be constructed in line with the principles of stochastic processes, to handle stochastic processes effects [4]. These models can offer more realistic representation of the physical system. Interesting enough, Runge-Kutta methods proves effective in handling stochastic differential equation theories that fits or handle stochastic processes, over some of the analytic methods [5, 6]. Therefore, there is a high need to develop and implement some stochastic Runge-Kutta methods for solving stochastic differential equations [7]. In this paper, an explicit Stochastic Rational Runge-Kutta method is derived based on the modified approach of stochastic Runge-Kutta methods for solving stochastic ordinary differential equations. Consider ordinary differential equations of the form,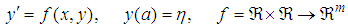 | (1) |
The general Rational Runge-Kutta schemes for the solution of (1) according to [8, 9, 10, 11, 12] is expressed as: 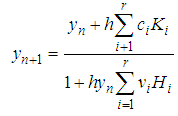 | (2) |
where
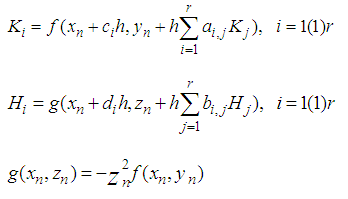 and
and 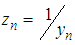 Consider the non-autonomous, one Wiener SDE of Stratonovich type:
Consider the non-autonomous, one Wiener SDE of Stratonovich type: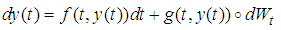 | (3) |
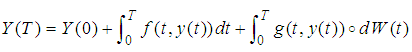 | (4) |
We shall assume a solution of the form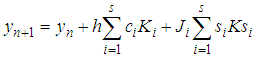 | (5) |
This now motivate us to formulate an s-stage explicit stochastic Rational Runge-Kutta (SRRK) methods for the solution of (3) as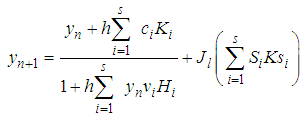 | (6) |
Where 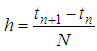 , N is a positive integer,
, N is a positive integer, 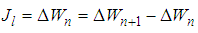

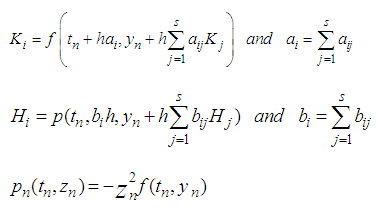 and
and 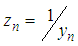

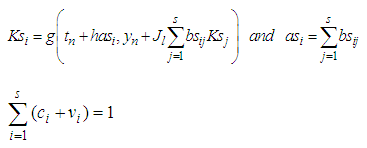 where
where 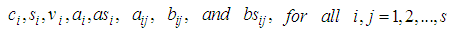 are constants to be determined. We can classify SRRK methods, as follows:If
are constants to be determined. We can classify SRRK methods, as follows:If 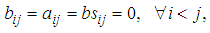 then the method is called semi-implicit.If
then the method is called semi-implicit.If 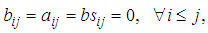 then the method is called explicit.Otherwise it is called implicit.Definition 1: (Strong convergence)We say that a discrete time approximation
then the method is called explicit.Otherwise it is called implicit.Definition 1: (Strong convergence)We say that a discrete time approximation 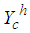 converges strongly with order
converges strongly with order 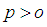 at time
at time 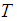 if there exist a positive constant
if there exist a positive constant  , which does not depend on the maximum step size h, and
, which does not depend on the maximum step size h, and 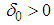 , such that
, such that
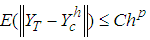 holds for each
holds for each 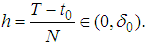
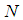 is the number of subintervals of the interval,
is the number of subintervals of the interval, 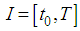 ,
, 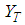 is the exact solution at
is the exact solution at 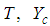 is the approximate solution at
is the approximate solution at 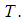 We shall employ the strong convergence principles in analysing our results.
We shall employ the strong convergence principles in analysing our results.
2. Derivation of the Methods
In order to derive the one-stage explicit SRRK methods, let 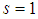 in (6) to obtain
in (6) to obtain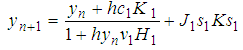 | (7) |
where
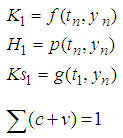
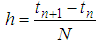 , N is a positive integer,
, N is a positive integer, 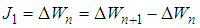 With
With
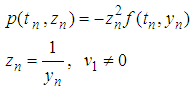 Expand the R.H.S of (7) binomially, simplify and neglect terms in h of order two and higher to obtain
Expand the R.H.S of (7) binomially, simplify and neglect terms in h of order two and higher to obtain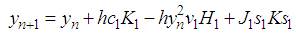 | (8) |
Expanding 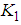 using Taylor series about
using Taylor series about 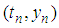 we have:
we have: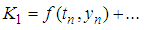 | (9) |
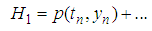 | (10) |
and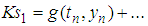 | (11) |
Substituting(9), (10) and (11) in the R.H.S of (8) we get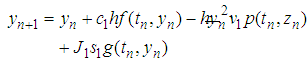 | (12) |
But 
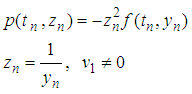 Then (12) becomes
Then (12) becomes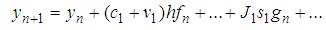 | (13) |
From Taylor series expansion of 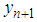 about
about 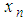 we get
we get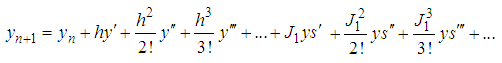 | (14) |
If we use the notations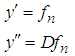 | (15) |
since 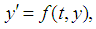 and let
and let 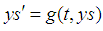 be the solution of the stochastic part denoted by ys and when:
be the solution of the stochastic part denoted by ys and when: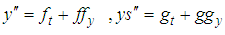 Therefore, (14) becomes
Therefore, (14) becomes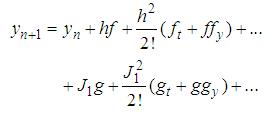 | (16) |
For consistency,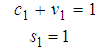 | (17) |
Which is the simultaneous equations to be solved in three unknowns 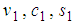 , where c1 is a free parameter.To determine a particular scheme of one-stage explicit Stochastic Rational Runge-Kutta Methods (SRRK):Case 1, let
, where c1 is a free parameter.To determine a particular scheme of one-stage explicit Stochastic Rational Runge-Kutta Methods (SRRK):Case 1, let
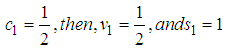 This gives
This gives 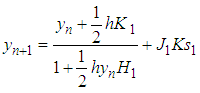 | (18) |
where
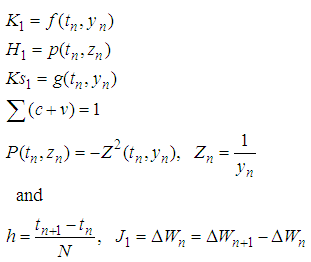 Where
Where 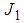 is Gaussian random normal distribution with mean zero and standard deviation one
is Gaussian random normal distribution with mean zero and standard deviation one 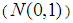 Case 2, if
Case 2, if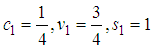 , we obtain
, we obtain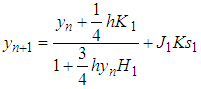 | (19) |
where 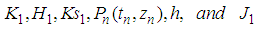 are as defined in (18)Case 3, if
are as defined in (18)Case 3, if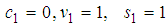 , then,
, then,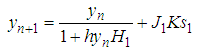 | (20) |
where 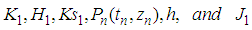 are as defined in (18)Case 4, if
are as defined in (18)Case 4, if
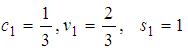
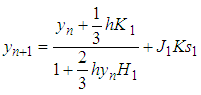 | (21) |
where 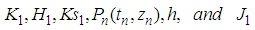 are as defined in (18)Thus, the schemes (18), (19), (20) and (21) are the one-stage SRRK methods.
are as defined in (18)Thus, the schemes (18), (19), (20) and (21) are the one-stage SRRK methods.
3. Stability Analysis
Theorem 1: (Convergence, [13])(i) Let the function 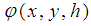 be continuously jointly as a function of its three arguments, in the region
be continuously jointly as a function of its three arguments, in the region 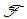 defined by
defined by 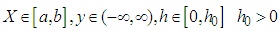 (ii) Let
(ii) Let 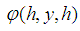 satisfy a Lipchitz condition of the form
satisfy a Lipchitz condition of the form 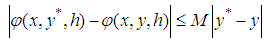 for all points
for all points 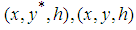 in
in 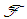 then the method
then the method 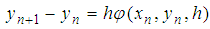 is convergent if and only if it is consistent.Theorem 2 [18]: For the test equation
is convergent if and only if it is consistent.Theorem 2 [18]: For the test equation 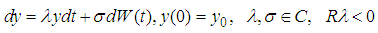 the Euler-Maruyama method is numerical stable in mean if
the Euler-Maruyama method is numerical stable in mean if 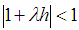 .Note that the stability condition
.Note that the stability condition 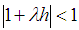 is the same as Euler method for ODEs according to Lambert (1991). In general the numerical stability conditions for the additive case are coincident with them for ODEs (Hermandez and Spigler, 1992).Theorem 3 [18]: If the Euler-Maruyama method satisfies the numerical stable condition in mean, i.e.
is the same as Euler method for ODEs according to Lambert (1991). In general the numerical stability conditions for the additive case are coincident with them for ODEs (Hermandez and Spigler, 1992).Theorem 3 [18]: If the Euler-Maruyama method satisfies the numerical stable condition in mean, i.e. 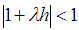 , the Euler-Maruyama method is asymptotically consistent in mean square. For the stability analysis of the derived schemes, we shall use the Shur method and utilize the principles of [14, 15, 16, 17, 18, 19], that states, the stability analysis of stochastic methods correspond with its deterministic counterpart. Using the test equation
, the Euler-Maruyama method is asymptotically consistent in mean square. For the stability analysis of the derived schemes, we shall use the Shur method and utilize the principles of [14, 15, 16, 17, 18, 19], that states, the stability analysis of stochastic methods correspond with its deterministic counterpart. Using the test equation 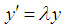 | (22) |
From (18)Expanding and truncating terms in h of second and higher orders, we obtain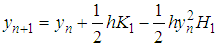 | (23) |
But 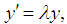 and
and 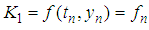 since
since 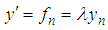

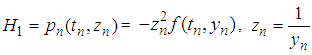 substituting these in (23), we get
substituting these in (23), we get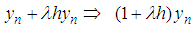 is the characteristic polynomial
is the characteristic polynomial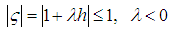 | (24) |
Therefore, (-2.0, 0) is the interval of the absolute stability of the one-stage scheme (18). Similarly, we can see that (18), (19), (20) and (21) all have the same interval of absolute stability. Which is called numerical stable in mean in stochastic sense.
4. Numerical Problems and Results
Problem 1Consider the SDE [6]
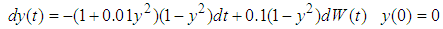 With the exact solution given by:
With the exact solution given by:
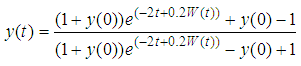 Problem 2Consider the SDE [20]
Problem 2Consider the SDE [20]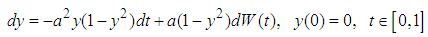 with exact solution
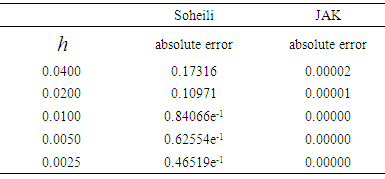
with exact solution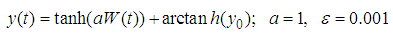 Therefore, the numerical solution using the explicit SRRK methods for the one-stage schemes as obtained in this work with absolute errors are given in the Tables 1 and 2 as seen below. The following notations will be used to represents results in the tables. PL, RAe1-3: Results from [6], Soheil, Results from [20] and JAk, Results obtained by our new methods.
Therefore, the numerical solution using the explicit SRRK methods for the one-stage schemes as obtained in this work with absolute errors are given in the Tables 1 and 2 as seen below. The following notations will be used to represents results in the tables. PL, RAe1-3: Results from [6], Soheil, Results from [20] and JAk, Results obtained by our new methods. Table 1. Numerical results of one-stage JAk explicit SRRK in comparison with [6] for Problem 1
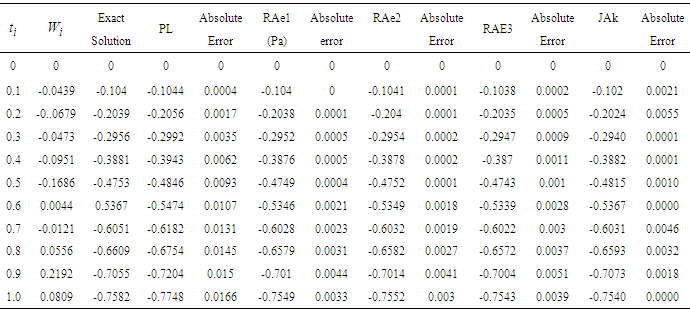 |
| |
|
Table 2. Numerical results of one-stage JAk explicit SRRK in comparison with [20] for Problem 2
 |
| |
|
5. Discussion of Results
With the one- stage explicit stochastic rational Runge-Kutta schemes (SRRK) denoted JAk in the numerical results tables. We derived family of four schemes of one-stage SRRK methods The family schemes for the one- stage were tested to solve numerical Problems 1and 2 from [6] and [20] respectively for some of the derived schemes as presented in tables 1 and 2. Matlab software (version 2010) was employed to run the simulations, based on normal distributed random numbers with mean zero and variance (standard deviation) one, i.e N(0,1). From Tables 1and 2 we can see the performance of our one stage schemes with the existing schemes in [6] and [20]. Also stability analysis of the one-stages developed were carried out using Schur method, in line with what we call mean and mean square stability principles in stochastic stability analysis discussed by some authors in section 3.0 and the stability analysis of the derived schemes showed they are bounded by the interval (-2.0, 0), just as that of deterministic one-stage explicit Runge-Kutta methods.
6. Conclusions
Clearly our one- stage schemes performs better in terms of convergence and accuracy, also the derived one -stage schemes was able to recover the results of their two stage schemes better. This means that our explicit SRRK methods is an alternative schemes to be used solve such problems. Also one is left with an options of choosing a scheme to work with in our case, unlike Euler Runge-Kutta method that has just a single scheme.
References
| [1] | Kloeden, P.E. & Platen, E. (1999). Numerical solution of stochastic differential equations (3rd.ed). Application of Mathematics, NewYork: Springer-Verlag, Berlin. |
| [2] | Burrage, K., & Burrage, P. M. And Tian, T. (2003). Numerical methods for strong solutions of stochastic differential equations: an overview. Retrieved from htt:/citseerx.ist.psu.edu/viewdoc/summary. |
| [3] | Sobezyk, K. (1991) Stochastic differential equations with applications to physics and engineering, Kluwer Academic Publisher, Dordrecht. SIAM Journal of Numerical Analysis 19(3), 604 – 613. |
| [4] | Soheili, R. A. (2008). Stochastic Runge-Kutta Method with weak and strong convergency. International Journal of Contemporary Mathematical Sciences, 3(9), 411 – 418. |
| [5] | Higham, J. D. (2001). An Algorithmic Introduction of numerical simulation of stochastic differential equations. SIAM Review, 43(3) 525-546. |
| [6] | Fadhel, S. F. & Abdulamear, A. A. (2011). Explicit Runge-Kutta Methods for solving stochastic differential equations. Journal of Researches Basrah ((science)),37(4) 301 –313. |
| [7] | Shreve, E. S. (2004). Stochastic calculus for Finance II. Continuous Time Model Springer Finance text book,USA. |
| [8] | Hong, Y. F. (1982). A class of A-stable or A(α) stable explicit schemes computational and asymptotic method for Boundary and interior layer proc. Of BAIL11 conference. Trinity college, Dublin. 236-241. |
| [9] | Okunbor D.I. (1987). Explicit rational Runge-Kutta schemes for stiff system of ordinary differential equations. M.Sc. Thesis. University of Benin, Benin city, Nigeria. |
| [10] | Odekunle, M. R. (2001). Some semi-implicit rational Runge-Kutta schemes. Bagale Journal of pure and Applied sciences, 1(1) 11-14. |
| [11] | Ademuliyi, A. R., Babatola, O.P. & Odekunle, M. R. (2002). Rationalised implicit Runge-Kutta schemes for the integration of stiff ordinary differential equations. Bagale Journal of pure and applied sciences, 2(2)16-23. |
| [12] | Abdulimen, C.E. & Uloko, A. J. (2012). A class of an implicit stage-two Rational Runge-Kutta Method for solution of Ordinary Differential Equations. Journal of Applied Mathematics & Bioinformatics, 2(3)17-31. |
| [13] | Lambert, J. D. (1973). Computational methods in ordinary differential equations. New York: John Wiley & Sons Chichester. |
| [14] | Milsten G.N. & Tretyakov M. (2004). Stochastic numerics for Mathematical Physics, Springer Verlag, Berlin. |
| [15] | Hernandez, D. B. & Spigler, R. (1992). “A-stability of Runge-Kutta methods for systems with additive noise’’, BIT 32,620-633. |
| [16] | Yuan, C. & Mao, X. 2004. “Stability in distribution of Numerical solutions for stochastic Differential equations’’, Stoch. anal. appl. 22,1133-1150. |
| [17] | Saito, Y. & Mitsui, T. (1993). “T-stability of numerical schemes for stochastic differential equations’’, WSSIAA 2,333-344. |
| [18] | Saito, Y. & Mitsui, T. (1996). “Stability analysis of numerical schemes for stochastic differential equations’’, SIAM J. Numer. Anal. 33, 2254-2267. |
| [19] | Platen, E. (1999). An introduction to Numerical Methods for stochastic differential equations, Acta, Numerica 8,197-246. |
| [20] | Soheili, R. A. (2008). Stochastic Runge-Kutta Method With Weak and Strong Convergency. International Journal of Contemporary Mathematical Sciences, 3(9), 411 – 418. |

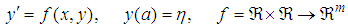
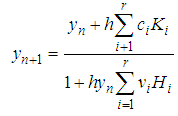

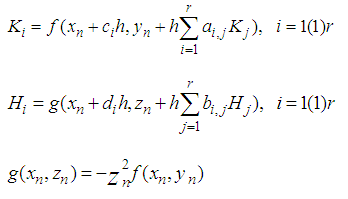 and
and 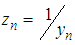 Consider the non-autonomous, one Wiener SDE of Stratonovich type:
Consider the non-autonomous, one Wiener SDE of Stratonovich type: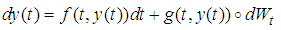
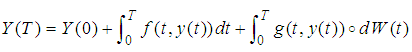
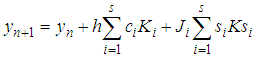
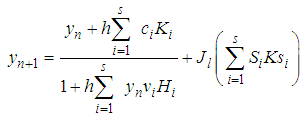
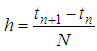 , N is a positive integer,
, N is a positive integer, 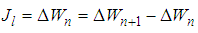

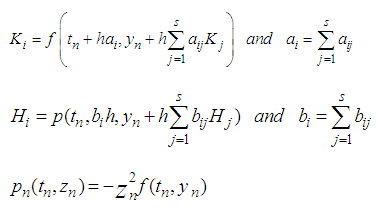 and
and 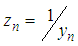

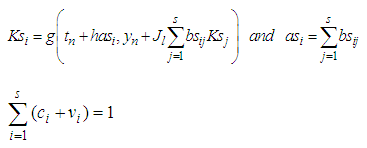 where
where 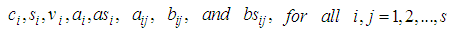 are constants to be determined. We can classify SRRK methods, as follows:If
are constants to be determined. We can classify SRRK methods, as follows:If 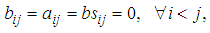 then the method is called semi-implicit.If
then the method is called semi-implicit.If 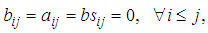 then the method is called explicit.Otherwise it is called implicit.Definition 1: (Strong convergence)We say that a discrete time approximation
then the method is called explicit.Otherwise it is called implicit.Definition 1: (Strong convergence)We say that a discrete time approximation 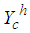 converges strongly with order
converges strongly with order 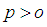 at time
at time 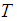 if there exist a positive constant
if there exist a positive constant 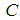 , which does not depend on the maximum step size h, and
, which does not depend on the maximum step size h, and 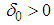 , such that
, such that
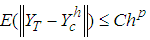 holds for each
holds for each 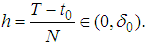
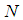 is the number of subintervals of the interval,
is the number of subintervals of the interval, 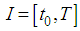 ,
, 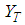 is the exact solution at
is the exact solution at 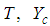 is the approximate solution at
is the approximate solution at 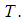 We shall employ the strong convergence principles in analysing our results.
We shall employ the strong convergence principles in analysing our results.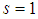 in (6) to obtain
in (6) to obtain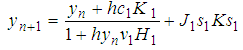

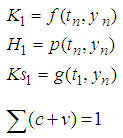
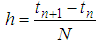 , N is a positive integer,
, N is a positive integer, 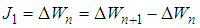 With
With
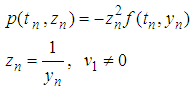 Expand the R.H.S of (7) binomially, simplify and neglect terms in h of order two and higher to obtain
Expand the R.H.S of (7) binomially, simplify and neglect terms in h of order two and higher to obtain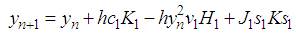
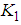 using Taylor series about
using Taylor series about 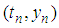 we have:
we have: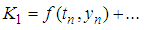
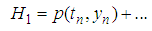
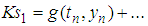
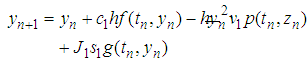

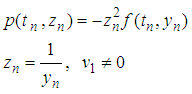 Then (12) becomes
Then (12) becomes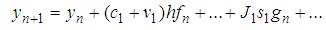
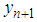 about
about 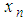 we get
we get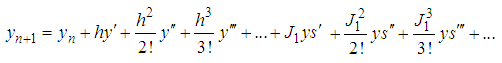
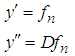
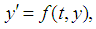 and let
and let 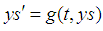 be the solution of the stochastic part denoted by ys and when:
be the solution of the stochastic part denoted by ys and when: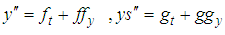 Therefore, (14) becomes
Therefore, (14) becomes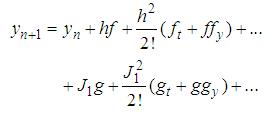
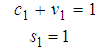
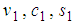 , where c1 is a free parameter.To determine a particular scheme of one-stage explicit Stochastic Rational Runge-Kutta Methods (SRRK):Case 1, let
, where c1 is a free parameter.To determine a particular scheme of one-stage explicit Stochastic Rational Runge-Kutta Methods (SRRK):Case 1, let
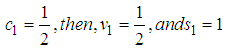 This gives
This gives 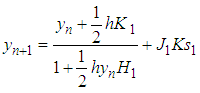

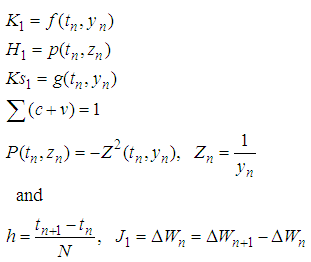 Where
Where 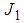 is Gaussian random normal distribution with mean zero and standard deviation one
is Gaussian random normal distribution with mean zero and standard deviation one 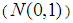 Case 2, if
Case 2, if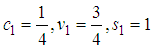 , we obtain
, we obtain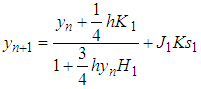
 are as defined in (18)Case 3, if
are as defined in (18)Case 3, if , then,
, then,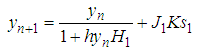
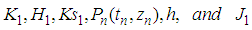 are as defined in (18)Case 4, if
are as defined in (18)Case 4, if
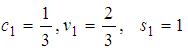
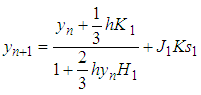
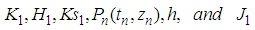 are as defined in (18)Thus, the schemes (18), (19), (20) and (21) are the one-stage SRRK methods.
are as defined in (18)Thus, the schemes (18), (19), (20) and (21) are the one-stage SRRK methods.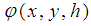 be continuously jointly as a function of its three arguments, in the region
be continuously jointly as a function of its three arguments, in the region  defined by
defined by 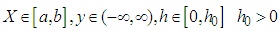 (ii) Let
(ii) Let 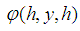 satisfy a Lipchitz condition of the form
satisfy a Lipchitz condition of the form 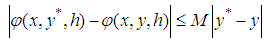 for all points
for all points 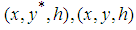 in
in 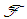 then the method
then the method 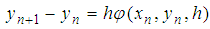 is convergent if and only if it is consistent.Theorem 2 [18]: For the test equation
is convergent if and only if it is consistent.Theorem 2 [18]: For the test equation 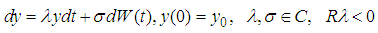 the Euler-Maruyama method is numerical stable in mean if
the Euler-Maruyama method is numerical stable in mean if 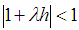 .Note that the stability condition
.Note that the stability condition 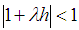 is the same as Euler method for ODEs according to Lambert (1991). In general the numerical stability conditions for the additive case are coincident with them for ODEs (Hermandez and Spigler, 1992).Theorem 3 [18]: If the Euler-Maruyama method satisfies the numerical stable condition in mean, i.e.
is the same as Euler method for ODEs according to Lambert (1991). In general the numerical stability conditions for the additive case are coincident with them for ODEs (Hermandez and Spigler, 1992).Theorem 3 [18]: If the Euler-Maruyama method satisfies the numerical stable condition in mean, i.e. 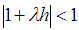 , the Euler-Maruyama method is asymptotically consistent in mean square. For the stability analysis of the derived schemes, we shall use the Shur method and utilize the principles of [14, 15, 16, 17, 18, 19], that states, the stability analysis of stochastic methods correspond with its deterministic counterpart. Using the test equation
, the Euler-Maruyama method is asymptotically consistent in mean square. For the stability analysis of the derived schemes, we shall use the Shur method and utilize the principles of [14, 15, 16, 17, 18, 19], that states, the stability analysis of stochastic methods correspond with its deterministic counterpart. Using the test equation 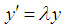
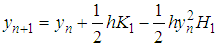
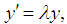 and
and 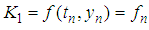 since
since 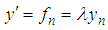

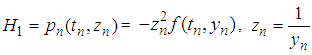 substituting these in (23), we get
substituting these in (23), we get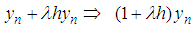 is the characteristic polynomial
is the characteristic polynomial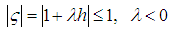

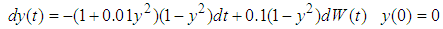 With the exact solution given by:
With the exact solution given by:
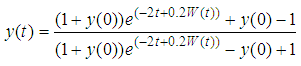 Problem 2Consider the SDE [20]
Problem 2Consider the SDE [20]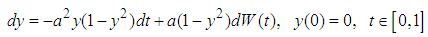 with exact solution
with exact solution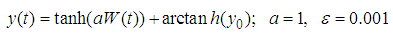 Therefore, the numerical solution using the explicit SRRK methods for the one-stage schemes as obtained in this work with absolute errors are given in the Tables 1 and 2 as seen below. The following notations will be used to represents results in the tables. PL, RAe1-3: Results from [6], Soheil, Results from [20] and JAk, Results obtained by our new methods.
Therefore, the numerical solution using the explicit SRRK methods for the one-stage schemes as obtained in this work with absolute errors are given in the Tables 1 and 2 as seen below. The following notations will be used to represents results in the tables. PL, RAe1-3: Results from [6], Soheil, Results from [20] and JAk, Results obtained by our new methods.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
