Olukunle Kehinde Olubowale1, Dipo Theophilus Akomolafe2, David Oni Awoyemi3
1Department of Mathematics and Statistics, College of Natural Sciences Joseph Ayo Babalola University, Ikeji Arakeji, Nigeria
2Departmentof Mathematical Sciences, Faculty of Science, Ondo State University of Science and Technology, Okitipupa, Nigeria
3Department of Industrial Mathematics, School of Science, Federal University of Technology, Akure, Nigeria
Correspondence to: Dipo Theophilus Akomolafe, Departmentof Mathematical Sciences, Faculty of Science, Ondo State University of Science and Technology, Okitipupa, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper established the existence of periodic oscillations to the fourth order nonlinear ordinary differential equations of the form 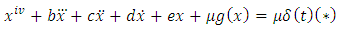
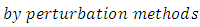 . Also established is a periodicoscillation to equation (*) of the form
. Also established is a periodicoscillation to equation (*) of the form 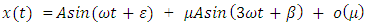 small 0, as
small 0, as 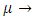
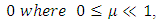 is very small and A, ω, , b, c, d, e, and
is very small and A, ω, , b, c, d, e, and 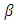 are constants; and
are constants; and 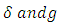 are continuous functions in their respective arguments that satisfy suitable growth restrictions such as
are continuous functions in their respective arguments that satisfy suitable growth restrictions such as 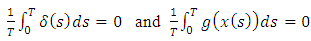 ,
, 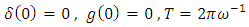 is the least period of oscillations and ω is the angular frequency of oscillations.
is the least period of oscillations and ω is the angular frequency of oscillations.
Keywords:
Differential Equation, Perturbation Method, Periodic Oscillations, Continuous Functions, Angular Frequency
Cite this paper: Olukunle Kehinde Olubowale, Dipo Theophilus Akomolafe, David Oni Awoyemi, Periodic Oscillations of a Fourth Order Non Linear Ordinary Differential Equations, American Journal of Computational and Applied Mathematics , Vol. 5 No. 4, 2015, pp. 101-104. doi: 10.5923/j.ajcam.20150504.01.
1. Introduction
Many physical problems arising from the motion electrical circuit theory and theory of elasticity can be represented by a fourth order ordinary differential equations of the form: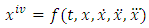 | (1) |
Where 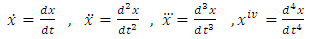
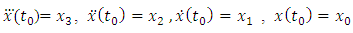 and the function f is continuous in all its argumentst,
and the function f is continuous in all its argumentst, 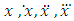 respectively and has continuous partial derivatives with respect to
respectively and has continuous partial derivatives with respect to 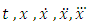 respectively.By solution to equation (1) we mean a function
respectively.By solution to equation (1) we mean a function 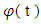 that satisfy equation (1). That is the equation
that satisfy equation (1). That is the equation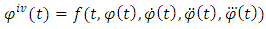 | (2) |
is an identity. An oscillatory solution to equation (1) is a solution 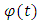 that has infinite number of zeros. The solution
that has infinite number of zeros. The solution 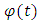 is a periodic solution if there exist a real number T such that
is a periodic solution if there exist a real number T such that 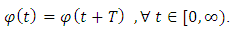 However, it is to be noted that
However, it is to be noted that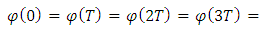 | (3) |
The number T is called the least period of the periodic oscillations.Particularly in this paper we shall examine equation (1) when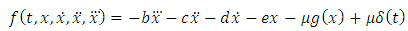 | (4) |
Hence equation (1) becomes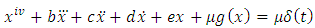 | (5) |
When 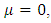 equation (5) becomes
equation (5) becomes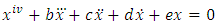 | (6) |
The functions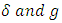 satisfy the following conditions:
satisfy the following conditions: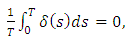 | (7) |
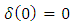 | (8) |
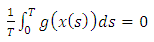 | (9) |
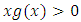 | (10) |
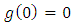 | (11) |
2. Objective of Research
The objectives of carrying out this research work are:a. to apply the perturbation methods to the periodic oscillations of a fourth order ordinary differential equation (5) and b. to bring out the relationship between the periodic oscillations of perturbed equation (5) and the periodic oscillations of the unperturbed equation (6).These objectives shall be achieved by accepting the fact that the periodic oscillations of the unperturbed linear fourth order ordinary differential equation (6) of the form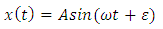 | (12) |
can be extended to the periodic oscillations of the form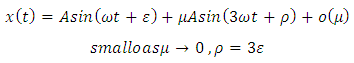 | (13) |
of perturbed fourth order nonlinear ordinary differential equation(5) due to the presence of additional correction term involving 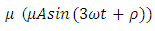 in equation (13).
in equation (13).
3. Problem Analysis
The first step is to consider a fourth order ordinary differential equations of the form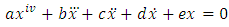 | (14) |
The interest here is in a bounded periodic oscillation. Let 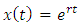 be a solution to equation (14) where r is a constant.
be a solution to equation (14) where r is a constant. 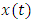 will be a bounded periodic oscillation when t is very large if r is a complex number with negative real part. That is r = -m + I n, where m and n are positive real numbers and I 2 = - 1.By substituting
will be a bounded periodic oscillation when t is very large if r is a complex number with negative real part. That is r = -m + I n, where m and n are positive real numbers and I 2 = - 1.By substituting 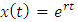 into the equation (9) we have the equation
into the equation (9) we have the equation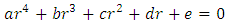 | (15) |
where a, b, c, d, e are constant real numbersEquation (15) is a quartic equationThus the equation (14) will have a bounded periodic oscillation if: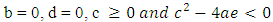 and since when
and since when 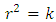 is a complex number, r is also a complex number. Furthermore, it is imperative to consider another case of interest. Using the substitution.
is a complex number, r is also a complex number. Furthermore, it is imperative to consider another case of interest. Using the substitution.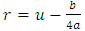 in equation(15) we have equation (15) becoming
in equation(15) we have equation (15) becoming 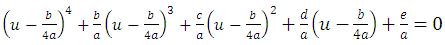 | (16) |
Expanding the power of the binomials in equation (16) and simplifying, we have the follow in g equation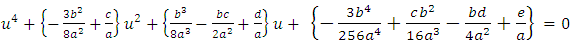 | (17) |
Now let 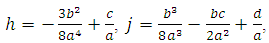 and
and 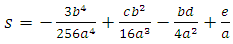 Equation (17) becomes
Equation (17) becomes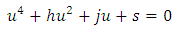 | (18) |
Equation (18) is a depressed quartic equation due to the absence of 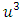 term in equation (18).Case II. If j = 0 we have a bi quadratic equation
term in equation (18).Case II. If j = 0 we have a bi quadratic equation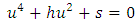 | (19) |
which is similar to what we have in case I. It is observed that if 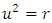 is a complex number, r is also a complex number.
is a complex number, r is also a complex number.
4. Methods
The methods of perturbation was used to establish the existence of periodic oscillation to equation (1). We now consider the equation (14) 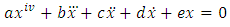 Without loss of generality we assume that a = 1, e = 1, d<0The essence of d < 0 is to ensure that we have negative damping which will prevent the oscillation from being blown up after some time. We now assume a periodic oscillatory solution of the form
Without loss of generality we assume that a = 1, e = 1, d<0The essence of d < 0 is to ensure that we have negative damping which will prevent the oscillation from being blown up after some time. We now assume a periodic oscillatory solution of the form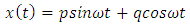 | (20) |
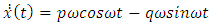 | (21) |
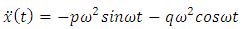 | (22) |
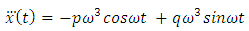 | (23) |
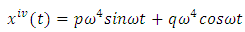 | (24) |
Substituting equations (20), (21), (22), (23), (24) into equation (14), we have the following equations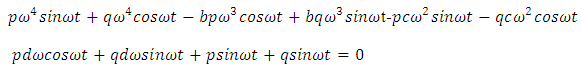 | (25) |
Putting 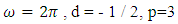 and q = 4 in equation (25) and after simplifying we have
and q = 4 in equation (25) and after simplifying we have Hence the fourth order ordinary differential equation
Hence the fourth order ordinary differential equation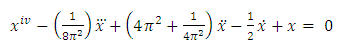 | (26) |
has the non-trivial periodic oscillation of the form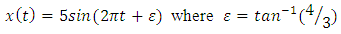
5. Results
The results are as follows:The following fourth order ordinary differential equations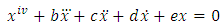 | (14) |
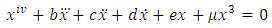 | (27) |
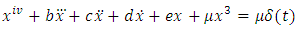 | (28) |
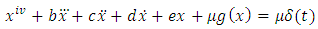 | (29) |
have periodic oscillations of the form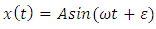 | (30) |
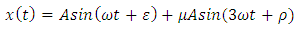 | (31) |
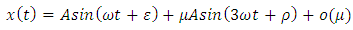 | (32) |
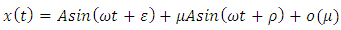 | (33) |
Small 0 as 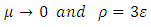 respectively where the functions
respectively where the functions 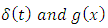 satisfy the following conditions
satisfy the following conditions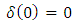 | (35) |
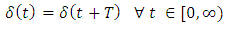 | (36) |
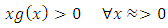 | (37) |
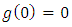 | (38) |
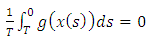 | (39) |
6. Proof of Results
Clearly, the trivial solution 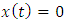 is a periodic oscillation to equations (14), (27), (28) and (29). Since equation (14) is a constant coefficient fourth order ordinary differential equation, its periodic oscillations
is a periodic oscillation to equations (14), (27), (28) and (29). Since equation (14) is a constant coefficient fourth order ordinary differential equation, its periodic oscillations 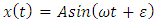 exist whenever b, c, d, e, ω satisfy the conditions
exist whenever b, c, d, e, ω satisfy the conditions 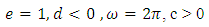
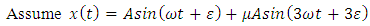 | (40) |
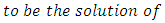 equation (27). Clearly all the conditions of the statement of our results are satisfied. Hence the expression (40) is a periodic oscillation to equation (27).Similarly there exist periodic oscillations of the form
equation (27). Clearly all the conditions of the statement of our results are satisfied. Hence the expression (40) is a periodic oscillation to equation (27).Similarly there exist periodic oscillations of the form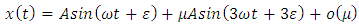 | (41) |
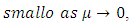 to equations (28) and (29).Also the zero solution
to equations (28) and (29).Also the zero solution 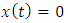 is a periodic oscillation to equations (14), (27), (28) and (29).
is a periodic oscillation to equations (14), (27), (28) and (29).
7. Discussion
The periodic oscillation as we have in expression (30) 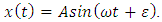 With A=5,
With A=5, 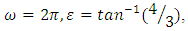 obtained for the equation (14) when
obtained for the equation (14) when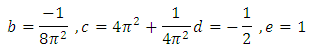 can be extended to the periodic oscillation of the nonlinear fourth order ordinary differential equations of the forms(27), (28) and (29), respectively, where
can be extended to the periodic oscillation of the nonlinear fourth order ordinary differential equations of the forms(27), (28) and (29), respectively, where 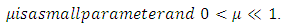 It should be noted that equations (27), (28), and (29) reduces to equation (14) when
It should be noted that equations (27), (28), and (29) reduces to equation (14) when 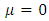 . Also the periodic oscillations (31), (32) and (33) obtained for equations (27), (28) and (29) respectively reduces to the periodic oscillation we have in (30) obtained for equation (14) when
. Also the periodic oscillations (31), (32) and (33) obtained for equations (27), (28) and (29) respectively reduces to the periodic oscillation we have in (30) obtained for equation (14) when 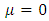 in equations (27), (28), (29) and expressions (31), (32) and (33).
in equations (27), (28), (29) and expressions (31), (32) and (33).
8. Conclusions
It has been established that periodic oscillations apart from the trivial solution 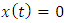 to equations (14), (27), (28), and (29) through systematic approach of constructing periodic oscillations by perturbation methods exist. Starting with the construction of a periodic oscillation (30) to a linear fourth order ordinary differential equation (14), we now extend this procedure to the construction of periodic oscillations to equations (27), (28), and (29) when
to equations (14), (27), (28), and (29) through systematic approach of constructing periodic oscillations by perturbation methods exist. Starting with the construction of a periodic oscillation (30) to a linear fourth order ordinary differential equation (14), we now extend this procedure to the construction of periodic oscillations to equations (27), (28), and (29) when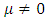 . The results can be extended to a wider class of fourth order nonlinear ordinary differential equations which we shall consider in our future presentations.
. The results can be extended to a wider class of fourth order nonlinear ordinary differential equations which we shall consider in our future presentations.
References
| [1] | Afuwape, F.O., Omari, P, and Zanolin, F (1989). Nonlinear perturbations of differential operators with non trivial kernel and applications to third –order periodic boundary value problems, Journal of Mathematical Analysis and Applications, Vol.143, No.1, pp 35 – 56. |
| [2] | Amster, P and Mariami, M.C., (2007). Oscillating solutions of a nonlinear fourth orderordinary differential equation, Journal of Mathematical Analysis and Applications, Vol.325, No.2, pp1133-1141. |
| [3] | Awoyemi, D.O.; (2005). Algorithmic collocation approach for direct solution of fourth order initial value problems of ordinary differential equations, International Journal of Computer Mathematics, Vo l .82, No.3, pp 321 – 329. |
| [4] | Bereanu, C., (2009), Periodic solutions of some fourth order nonlinear differential Equations, Non linear Analysis Theory, Methods and Applications, Vol.71 , No.1-2, pp 53 - 57. |
| [5] | Chaparova, J., (2002). Existence and numerical approximations of periodic solutions of semi linear fourth order differential equations, Journal of Mathematical Analysis and Applications, Vol.273 , No.1 , pp 121 - 136. |
| [6] | Cronin-Scalon, J., (1977). Some Mathematics of Biological Oscillations, SIAM Review, Vol. 19, No.1, pp 100 - 137. |
| [7] | Friderichs, K.O., (1949) On Nonlinear Vibrations Theory ss, Studies in Nonlinear Vibrations Theory, Institute of Mathematics and Mechanics, New York University, New York, NY, USA. |
| [8] | Fuzhong, C. Qingdao, H. and Shaoyun, S. (2000). Existence and Uniqueness of Periodic Solutions for (2n+1)th –order differential equations, Journal of Mathematical Analysis and Applications , Vol.241, No.1, pp 1 - 9. |
| [9] | Hardy, H. Litttlewood, J.E., and Polyya, G., (1964). Inequalities, Cambridge University Press, London, UK. |
| [10] | Li, Y. (2006). Existence and uniqueness for higher order periodic boundary value problems under spectral separation conditions, Journal of Mathematical Analysis and Applications, Vol.322, No.2, pp 530 - 539. |
| [11] | Li, Y., (2009). On the existence and uniqueness for higher order periodic boundary value problems, Nonlinear Analysis: Theory, Methods and Applications, Vol.70, No.2, pp. 711 - 718. |
| [12] | Li, W., (2001), Periodic solutions for 2kth order ordinary differential equations with resonance, Journal of Mathematical Analysis and Applications, Vol.259, No.1, pp 157 - 167. |
| [13] | Liu, B., and Huang, L., (2006). Existence and Uniqueness of periodic solutions for a kind of first order neutral functional differential equations, Journal of Mathematical Analysis and Applications, Vol.322, No.1, pp. 121 - 132. |
| [14] | Mawhin, J. (1979). Topological Degree Methods in Nonlinear Boundary Value Problems, Vol.40, American Mathematical Society, Providence, RI, USA. |
| [15] | Mawhin, J. (1974), Periodic solutions of some vector retarded functional differential equations, Journal of Mathematical Analysis and Applications, Vol.45, pp. 588 - 603. |
| [16] | Olubowale, K.O., and Akomolafe, D.T. (2012), A note on the existence of periodic solutions of a class of perturbed second order nonlinear ordinary differential equations, American Journal of Mathematics and Statistics, Vol.2, No.2 |

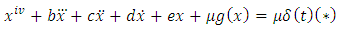
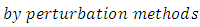 . Also established is a periodicoscillation to equation (*) of the form
. Also established is a periodicoscillation to equation (*) of the form 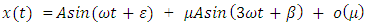 small 0, as
small 0, as 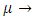
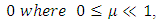 is very small and A, ω, , b, c, d, e, and
is very small and A, ω, , b, c, d, e, and 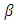 are constants; and
are constants; and 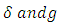 are continuous functions in their respective arguments that satisfy suitable growth restrictions such as
are continuous functions in their respective arguments that satisfy suitable growth restrictions such as 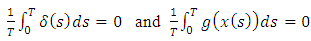 ,
, 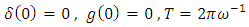 is the least period of oscillations and ω is the angular frequency of oscillations.
is the least period of oscillations and ω is the angular frequency of oscillations.
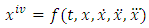
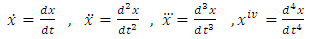
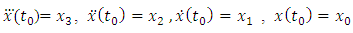 and the function f is continuous in all its argumentst,
and the function f is continuous in all its argumentst, 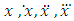 respectively and has continuous partial derivatives with respect to
respectively and has continuous partial derivatives with respect to 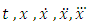 respectively.By solution to equation (1) we mean a function
respectively.By solution to equation (1) we mean a function 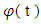 that satisfy equation (1). That is the equation
that satisfy equation (1). That is the equation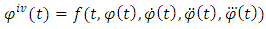
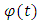 that has infinite number of zeros. The solution
that has infinite number of zeros. The solution 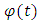 is a periodic solution if there exist a real number T such that
is a periodic solution if there exist a real number T such that 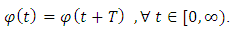 However, it is to be noted that
However, it is to be noted that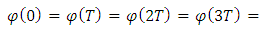
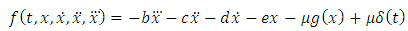
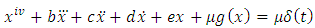
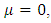 equation (5) becomes
equation (5) becomes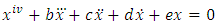
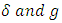 satisfy the following conditions:
satisfy the following conditions: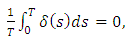
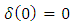
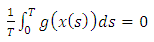
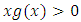
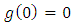
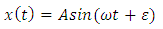
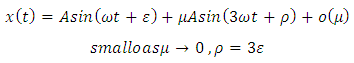
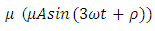 in equation (13).
in equation (13).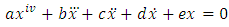
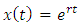 be a solution to equation (14) where r is a constant.
be a solution to equation (14) where r is a constant. 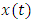 will be a bounded periodic oscillation when t is very large if r is a complex number with negative real part. That is r = -m + I n, where m and n are positive real numbers and I 2 = - 1.By substituting
will be a bounded periodic oscillation when t is very large if r is a complex number with negative real part. That is r = -m + I n, where m and n are positive real numbers and I 2 = - 1.By substituting 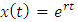 into the equation (9) we have the equation
into the equation (9) we have the equation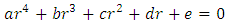
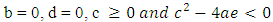 and since when
and since when 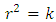 is a complex number, r is also a complex number. Furthermore, it is imperative to consider another case of interest. Using the substitution.
is a complex number, r is also a complex number. Furthermore, it is imperative to consider another case of interest. Using the substitution.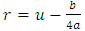 in equation(15) we have equation (15) becoming
in equation(15) we have equation (15) becoming 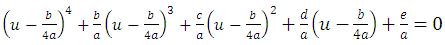
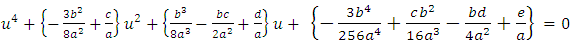
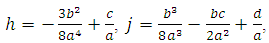 and
and 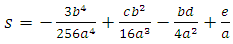 Equation (17) becomes
Equation (17) becomes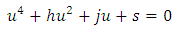
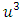 term in equation (18).Case II. If j = 0 we have a bi quadratic equation
term in equation (18).Case II. If j = 0 we have a bi quadratic equation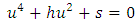
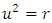 is a complex number, r is also a complex number.
is a complex number, r is also a complex number.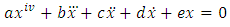 Without loss of generality we assume that a = 1, e = 1, d<0The essence of d < 0 is to ensure that we have negative damping which will prevent the oscillation from being blown up after some time. We now assume a periodic oscillatory solution of the form
Without loss of generality we assume that a = 1, e = 1, d<0The essence of d < 0 is to ensure that we have negative damping which will prevent the oscillation from being blown up after some time. We now assume a periodic oscillatory solution of the form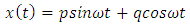
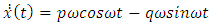
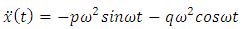
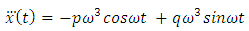
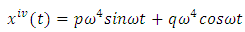
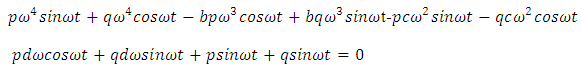
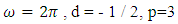 and q = 4 in equation (25) and after simplifying we have
and q = 4 in equation (25) and after simplifying we have Hence the fourth order ordinary differential equation
Hence the fourth order ordinary differential equation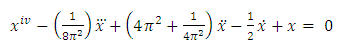
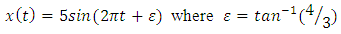
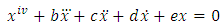
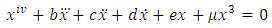
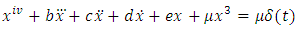
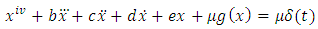
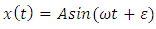
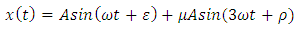
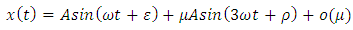
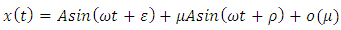
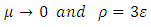 respectively where the functions
respectively where the functions 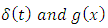 satisfy the following conditions
satisfy the following conditions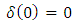
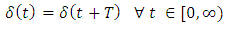
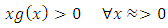
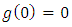
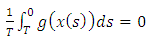
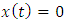 is a periodic oscillation to equations (14), (27), (28) and (29). Since equation (14) is a constant coefficient fourth order ordinary differential equation, its periodic oscillations
is a periodic oscillation to equations (14), (27), (28) and (29). Since equation (14) is a constant coefficient fourth order ordinary differential equation, its periodic oscillations 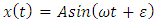 exist whenever b, c, d, e, ω satisfy the conditions
exist whenever b, c, d, e, ω satisfy the conditions 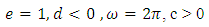
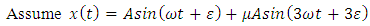
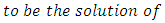 equation (27). Clearly all the conditions of the statement of our results are satisfied. Hence the expression (40) is a periodic oscillation to equation (27).Similarly there exist periodic oscillations of the form
equation (27). Clearly all the conditions of the statement of our results are satisfied. Hence the expression (40) is a periodic oscillation to equation (27).Similarly there exist periodic oscillations of the form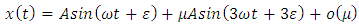
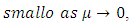 to equations (28) and (29).Also the zero solution
to equations (28) and (29).Also the zero solution 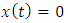 is a periodic oscillation to equations (14), (27), (28) and (29).
is a periodic oscillation to equations (14), (27), (28) and (29).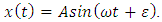 With A=5,
With A=5, 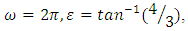 obtained for the equation (14) when
obtained for the equation (14) when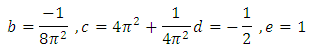 can be extended to the periodic oscillation of the nonlinear fourth order ordinary differential equations of the forms(27), (28) and (29), respectively, where
can be extended to the periodic oscillation of the nonlinear fourth order ordinary differential equations of the forms(27), (28) and (29), respectively, where 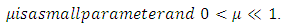 It should be noted that equations (27), (28), and (29) reduces to equation (14) when
It should be noted that equations (27), (28), and (29) reduces to equation (14) when 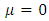 . Also the periodic oscillations (31), (32) and (33) obtained for equations (27), (28) and (29) respectively reduces to the periodic oscillation we have in (30) obtained for equation (14) when
. Also the periodic oscillations (31), (32) and (33) obtained for equations (27), (28) and (29) respectively reduces to the periodic oscillation we have in (30) obtained for equation (14) when 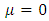 in equations (27), (28), (29) and expressions (31), (32) and (33).
in equations (27), (28), (29) and expressions (31), (32) and (33).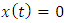 to equations (14), (27), (28), and (29) through systematic approach of constructing periodic oscillations by perturbation methods exist. Starting with the construction of a periodic oscillation (30) to a linear fourth order ordinary differential equation (14), we now extend this procedure to the construction of periodic oscillations to equations (27), (28), and (29) when
to equations (14), (27), (28), and (29) through systematic approach of constructing periodic oscillations by perturbation methods exist. Starting with the construction of a periodic oscillation (30) to a linear fourth order ordinary differential equation (14), we now extend this procedure to the construction of periodic oscillations to equations (27), (28), and (29) when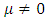 . The results can be extended to a wider class of fourth order nonlinear ordinary differential equations which we shall consider in our future presentations.
. The results can be extended to a wider class of fourth order nonlinear ordinary differential equations which we shall consider in our future presentations.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML