Rongdong Wang, Aden Ahmed, Jose Gutierrez
Department of Mathematics, Texas A&M University – Kingsville, Texas, USA
Correspondence to: Aden Ahmed, Department of Mathematics, Texas A&M University – Kingsville, Texas, USA.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We develop a Maple code that computes the solutions of two-person non-cooperative games. When the bimatrix game of any two-player, two-strategy, including bimatrix games with symbolic entries, is inputted into our Maple package, the program outputs all the Nash equilibrium strategy pairs (pure and/or mixed) along their corresponding payoffs. When the bimatrix game of any two-player, m×n strategy game is inputted into our Maple package, the program outputs only the pure Nash equilibrium strategy pairs along their corresponding payoffs.
Keywords:
Non-cooperative bimatrix games, Payoff function, Nash equilibrium, Job market game, Evolutionary game
Cite this paper: Rongdong Wang, Aden Ahmed, Jose Gutierrez, Computation of Nash Equilibria of Two-Person Non-Cooperative Games with Maple, American Journal of Computational and Applied Mathematics , Vol. 5 No. 3, 2015, pp. 80-87. doi: 10.5923/j.ajcam.20150503.02.
1. Introduction
The Theory of Games concerns the mathematics of decision making. It provides a general framework within which both cooperation and competition among independent agents may be modeled and gives powerful tools for analyzing these models. A game is said to be non-cooperative if each agent involved pursues his or her own interests which are partially conflicting with others’. Non-cooperative games are important tools which are extensively used in economics, social sciences, political science, computer science, biology, and in others fields. The main goal in game theory is the identification of potential Nash equilibria of a given game. The calculation of Nash Equilibria by hand is often tedious and time consuming even when the game is fairly small and may be impossible for large games. Because of these difficulties, calculations of Nash equilibria readily lend themselves to computer programming. Computation of Nash equilibria has been extensively studied and programs for finding Nash equilibria are available. However, all the existing methods and programs are numerical in nature and therefore cannot be used if the payoff matrices in a game contain entries that are parameters or symbolic values. However, in many applications of game theory, the bimatrix game contains entries which are parameters, hence the need to develop a new program. The following examples illustrate bimatrix games with entries that are parameters.
1.1. The Job Market ([1], Page 130-131)
Firms 1 and 2 have one opening each for which they are offering salaries 2a and 2b, respectively. Two players (job seekers) are competing for these two openings. Each player can apply to only one of the positions and the players must simultaneously decide whether to apply to Firm 1 or to Firm 2. If only one of the players applies for a job, he or she gets it; if both apply for the same position, the concerned firm hires one of them at random, each player being equally likely to be selected. The following bimatrix game models this problem.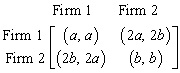 | (1) |
In this bimatrix, the entries (2a, 2b) and (2b, 2a) are self-explanatory. The entry (a, a) is obtained as follows. If both players apply to the same firm, then, because it was assumed that the firm will select an applicant at random, each can expect a payoff of half the salary. A similar argument justifies the entry (b, b). Clearly, the analysis of this game depends on the values and relationship of and between the parameters a and b. Depending on the cases 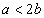 and
and 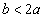 (the two salaries are not too far out of line with each other),
(the two salaries are not too far out of line with each other), 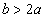 (Firm 2’s position pays very well), and
(Firm 2’s position pays very well), and 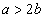 (Firm 1’s position pays very well), we will see that the nature of Nash equilibria will change from one case to the other. Note that numerical programs will not be helpful in solving this problem as the entries in the bimatrix game are all given as parameters. We will discuss the solution of this game in details in Section 4.
(Firm 1’s position pays very well), we will see that the nature of Nash equilibria will change from one case to the other. Note that numerical programs will not be helpful in solving this problem as the entries in the bimatrix game are all given as parameters. We will discuss the solution of this game in details in Section 4.
1.2. An Evolutionary Game ([2], page 282-283)
Two birds of the same species compete for a territory whose value in terms of evolutionary fitness is 2a. Each bird can adopt a hawkish or dovelike strategy in a simultaneous-move game. If both behave like doves, they split the territory. If one behaves like a dove and the other like a hawk, the hawk gets the territory. If both behave like hawks, there is a fight. The evolutionary fitness of a bird that has to fight is b. Assume that each bird is equally likely to win the fight and hence gain the territory. However, the fight is costly because of the risk of injury. We will use the model c = a – b, where c represents the cost of fighting. The following bimatrix game models this problem.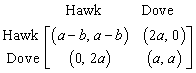 | (2) |
What should the birds do? We will analyze this game in each of the two situations where a > b (The moderate option: the territory is worth fighting for) and a ≤ b (The nuclear option: it is too costly to fight). We observe that this game cannot be also solved by numerical method. We will give the complete analysis of this game in Section 4.In order to calculate the Nash equilibria of a game whose payoff matrix contains symbols, the use of a computer algebra system is most suited. We will use the mathematical software Maple [3] to perform the symbolic computation. We propose a Maple package which can perform numerical as well as symbolic computations of Nash equilibria of two-person non-cooperative non-constant games. Our package can also find all pure Nash equilibria of non-cooperative m×n matrix games. However, it can only calculate and determine the mixed Nash equilibria of 2×2 games. We believe that this package will be a very useful tool for researchers in game theory as well as educators and students.
2. Nash Equilibrium Computation
We begin by recalling a few formal definitions of the game theoretic terms employed in this paper.Definition 2.1 A finite two-person non-cooperative game G is the tuple (S, T, A, B), where S and T are nonempty finite sets, the so called pure strategies for Player 1 and Player 2, respectively, and A and B are m×n matrices with real entries, the so called payoff matrices for Player 1 and Player 2, respectively. We observe that a finite two-person game is completely determined by its bimatrix, a matrix whose entries are pairs of real numbers. For example in the game whose bimatrix is given below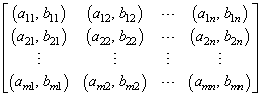 | (3) |
Player 1 has access to exactly m pure strategies, that is 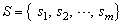 while Player 2 has at her disposal n pure strategies, namely
while Player 2 has at her disposal n pure strategies, namely 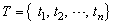 . The game is played as follows. Simultaneously, Player 1 chooses
. The game is played as follows. Simultaneously, Player 1 chooses 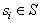 and Player 2 chooses
and Player 2 chooses 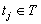 , each unaware of the choice of the other. Then their choices are made known and Player 1 wins the amount
, each unaware of the choice of the other. Then their choices are made known and Player 1 wins the amount 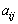 and Player 2 wins the amount
and Player 2 wins the amount 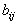 . This bimatrix can be broken up into two matrices A and B, the payoff matrices of Player 1 and Player 2, respectively, as shown below.
. This bimatrix can be broken up into two matrices A and B, the payoff matrices of Player 1 and Player 2, respectively, as shown below.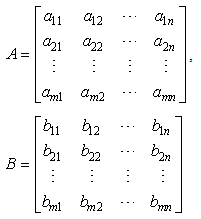 | (4) |
We say that a game G = (S, T, A, B) defined as above is zero-sum if 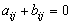 for all
for all 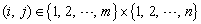 . It is constant-sum if
. It is constant-sum if 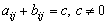 for all i and j. Otherwise, it is called a non-constant game.The main goal in game theory is the identification of some special strategic profiles. For example, given a fixed strategy t* ϵ T of the opponent, Player 1 would like to identify a best reply strategy, that is, a strategy s*ϵ S that delivers a utility at least as great than any other strategy s ϵ S. In symbols, this means that
for all i and j. Otherwise, it is called a non-constant game.The main goal in game theory is the identification of some special strategic profiles. For example, given a fixed strategy t* ϵ T of the opponent, Player 1 would like to identify a best reply strategy, that is, a strategy s*ϵ S that delivers a utility at least as great than any other strategy s ϵ S. In symbols, this means that 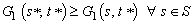 , where the payoff functions G1 and G2 are defined as
, where the payoff functions G1 and G2 are defined as 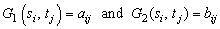 .The situation when both players have chosen such a strategy is of fundamental importance in game theory and described by the following definition.
.The situation when both players have chosen such a strategy is of fundamental importance in game theory and described by the following definition.
2.1. Definition (Pure Nash Equilibrium)
Let G be a finite two-person non-cooperative game. A pure Nash equilibrium (PNE) for G is a strategy profile 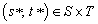 such that
such that 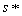 is a best reply to
is a best reply to 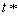 and
and 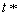 is a best reply to
is a best reply to 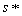 . In symbols,
. In symbols, 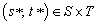 is a Nash equilibrium in G if and only if
is a Nash equilibrium in G if and only if 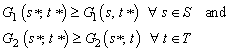 | (5) |
The above inequalities indicate that no player can increase his/her payoffs by unilaterally deviating from his or her equilibrium strategy or that at equilibrium a player’s opponent is indifferent to that player’s strategic choice.Given a game G, a Nash equilibrium may not exist amongst the pure strategy profiles. As an example, consider the 2×2 non-cooperative game whose bimatrix game is given by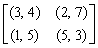 | (6) |
In this game, there is no pair 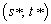 such that
such that 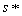 is a best reply to
is a best reply to 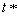 and
and 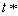 is a best reply to
is a best reply to 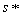 . Therefore, this game admits no Nash equilibria in pure strategies. Fortunately, game theorists usually extend the game G by enlarging the domain and extending the payoff functions. A standard extension of this point is to consider for each player the set of mixed strategies, that is, the sets of probability distributions over S and T. If X is a nonempty finite set, say.X = {x1, x2, …, xn}, we denote the probability distributions over X by
. Therefore, this game admits no Nash equilibria in pure strategies. Fortunately, game theorists usually extend the game G by enlarging the domain and extending the payoff functions. A standard extension of this point is to consider for each player the set of mixed strategies, that is, the sets of probability distributions over S and T. If X is a nonempty finite set, say.X = {x1, x2, …, xn}, we denote the probability distributions over X by 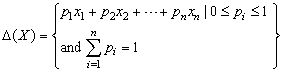 | (7) |
Note that one can embed X into Δ(X) by considering the element xi in X as mapped to the probability distribution which assigns 1 to xi and 0 to everything else.For a finite two-person non-cooperative game G = (S, T, A, B) defined as above, we observe that selecting a mixed strategy for Player 1 is tantamount to selecting a vector 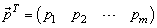 | (8) |
where Player 1 uses pure strategy si with probability pi. Similarly, a mixed strategy for Player 2 is a vector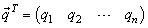 | (9) |
where Player 2 uses pure strategy tj with probability qj. Now, we extend the game G to a new larger game Gmix in the sense of the following definition.
2.2. Definition (Mixed Game)
Let G = (S, T, A, B) be a finite two-person non-cooperative game. The associated two-person mixed game, Gmix, is a tuple 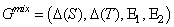 , where
, where 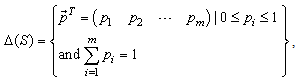 | (10) |
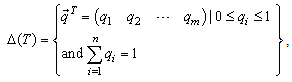 | (11) |
and 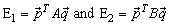 are the expected payoffs to Player 1 and Player 2, respectively.Note that the game Gmix contains the game G.Nash’s Theorem [4] says that if S and T are finite as above, then there always exists at least one equilibrium in Gmix. Note that every equilibrium in G is also an equilibrium in Gmix. Hence, throughout, we will only look for the equilibria in the mixed game as they also include the equilibria of G.
are the expected payoffs to Player 1 and Player 2, respectively.Note that the game Gmix contains the game G.Nash’s Theorem [4] says that if S and T are finite as above, then there always exists at least one equilibrium in Gmix. Note that every equilibrium in G is also an equilibrium in Gmix. Hence, throughout, we will only look for the equilibria in the mixed game as they also include the equilibria of G.
2.3. Definition (Mixed Nash Equilibrium)
Let G = (S, T, A, B) be a finite two-person non-cooperative game and let 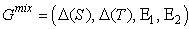 be its associated mixed game. A mixed Nash equilibrium (MNE) for Gmix is a strategy profile
be its associated mixed game. A mixed Nash equilibrium (MNE) for Gmix is a strategy profile 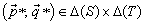 such that
such that 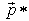 is a best reply to
is a best reply to 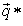 and
and 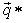 is a best reply to
is a best reply to 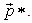 In symbols,
In symbols, 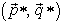 is a Nash equilibrium in Gmix if and only if
is a Nash equilibrium in Gmix if and only if 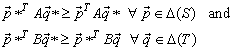 | (12) |
If we set 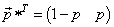 and
and 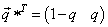 , it is an easy exercise to show that
, it is an easy exercise to show that 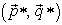 is a Nash equilibrium if and only if
is a Nash equilibrium if and only if 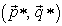 is a solution of the linear programming problem
is a solution of the linear programming problem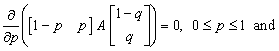
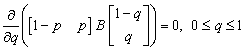 We develop a Maple procedure called nashp that produces all pure Nash equilibria of all m×n matrix games. The Maple codes in this procedure are directly based on the definition of pure Nash equilibrium. In contrast, to identify the mixed Nash equilibria of 2×2 games, the Maple procedure which we call nashm will be used. The structure of this procedure is based on solving linear equations and inequalities which are related to the payoff matrices.Let G = (S, T, A, B) be a two-person, two-strategy non-cooperative game, that is, both sets S and T contains each exactly two elements. Let
We develop a Maple procedure called nashp that produces all pure Nash equilibria of all m×n matrix games. The Maple codes in this procedure are directly based on the definition of pure Nash equilibrium. In contrast, to identify the mixed Nash equilibria of 2×2 games, the Maple procedure which we call nashm will be used. The structure of this procedure is based on solving linear equations and inequalities which are related to the payoff matrices.Let G = (S, T, A, B) be a two-person, two-strategy non-cooperative game, that is, both sets S and T contains each exactly two elements. Let 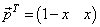 and
and 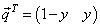 be Player 1 and Player 2 mixed strategies, respectively. Then, the Maple command solve is utilized to solve linear systems of equations subject to inequalities. The system with constraints
be Player 1 and Player 2 mixed strategies, respectively. Then, the Maple command solve is utilized to solve linear systems of equations subject to inequalities. The system with constraints 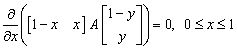 | (13) |
and 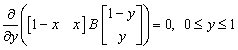 | (14) |
symbolically gives the Nash equilibrium strategies for Player 1 and Player 2, respectively. This method is easy and quick as opposed to the graphical method which is extensively used in the literature [5, 6]. This procedure returns as output mixed Nash equilibria which are exact, however, it misses to provide the pure Nash equilibria when they exist. Fortunately, procedures nashp and nashm can be used together to identify all Nash equilibria (pure and mixed) of 2×2 games. Moreover, we create the Maple procedure nasha which calls both nashp and nashm. This procedure will be utilized to find all Nash equilibria of 2×2 non-constant non-cooperative games.
3. The Maple Package
We utilize the Maple function Module to create a Maple package nashe which includes the procedures nashp, nashm, and nashi as follows.
 The following command makes the package work in Maple.Savelib (nashe);The input of every procedure in the package is a bimatrix, that is, a matrix whose entries are ordered pairs of real numbers. In each pair, the first number is Player 1’s payoff and the second number is Player 2’s payoff. For example, if the payoff matrix for Player 1 is given by
The following command makes the package work in Maple.Savelib (nashe);The input of every procedure in the package is a bimatrix, that is, a matrix whose entries are ordered pairs of real numbers. In each pair, the first number is Player 1’s payoff and the second number is Player 2’s payoff. For example, if the payoff matrix for Player 1 is given by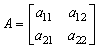 | (15) |
and the payoff matrix for Player 2 is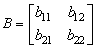 | (16) |
Then, the input matrix for a procedure is written as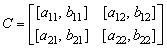 | (17) |
In particular, if 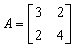 and
and 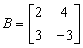 are the payoff matrices to Player 1 and Player 2, respectively, then the input matrix may be typed into Maple asC:=Matrix([[[3, 2], [2, 4]], [[2, 3], [4, – 3]]])In order to use a procedure, say nasha, one needs to type only once with (nashe) and nasha(C). Of course, one will need to press the Enter key in order to have each Maple command executed. The output of a procedure is a set of Nash equilibria followed by their corresponding payoffs. For example, a Nash equilibrium output has the following format.[ [Player 1’s optimal strategy], [Plyer 2’s optimal strategy], payoff for Player 1, Payoff for Player 2]
are the payoff matrices to Player 1 and Player 2, respectively, then the input matrix may be typed into Maple asC:=Matrix([[[3, 2], [2, 4]], [[2, 3], [4, – 3]]])In order to use a procedure, say nasha, one needs to type only once with (nashe) and nasha(C). Of course, one will need to press the Enter key in order to have each Maple command executed. The output of a procedure is a set of Nash equilibria followed by their corresponding payoffs. For example, a Nash equilibrium output has the following format.[ [Player 1’s optimal strategy], [Plyer 2’s optimal strategy], payoff for Player 1, Payoff for Player 2]
4. Applications
Our first application concerns an example of a game taken from [1], p. 157-160. The bimatrix game is given by 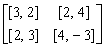 | (18) |
Running this game through our Maple package, we obtain the following sequence of outputs. This game has no equilibria in pure strategies. However, the game admits a unique equilibrium in mixed strategies where Player 1 uses his first and second pure strategies with probabilities 3/4 and 1/4, respectively, and Player 2 uses her first and second pure strategies with probabilities 2/3 and 1/3, respectively. This mixed strategy equilibrium pays out 8/3 to Player 1 and 9/4 to Player 2.Our second example is also a game taken from [1], p. 160-162 with bimatrix game given by
This game has no equilibria in pure strategies. However, the game admits a unique equilibrium in mixed strategies where Player 1 uses his first and second pure strategies with probabilities 3/4 and 1/4, respectively, and Player 2 uses her first and second pure strategies with probabilities 2/3 and 1/3, respectively. This mixed strategy equilibrium pays out 8/3 to Player 1 and 9/4 to Player 2.Our second example is also a game taken from [1], p. 160-162 with bimatrix game given by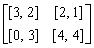 | (19) |
Running this game through our Maple package, we obtain the following sequence of outputs. This game admits two Nash equilibria in pure strategies, namely,
This game admits two Nash equilibria in pure strategies, namely, 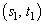 and
and 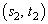 and the corresponding payoffs to the players are (3, 2) and (4, 4), respectively. There is a unique mixed strategy equilibrium where Player 1 employs each of his pure strategies with equal probability and Player 2 uses her first and second pure strategies with probabilities 2/5 and 3/5, respectively. This mixed strategy equilibrium pays out 12/5 to Player 1 and 5/2 to Player 2.Our third example is also a game taken from [1], p. 162-163 with bimatrix game given by
and the corresponding payoffs to the players are (3, 2) and (4, 4), respectively. There is a unique mixed strategy equilibrium where Player 1 employs each of his pure strategies with equal probability and Player 2 uses her first and second pure strategies with probabilities 2/5 and 3/5, respectively. This mixed strategy equilibrium pays out 12/5 to Player 1 and 5/2 to Player 2.Our third example is also a game taken from [1], p. 162-163 with bimatrix game given by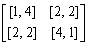 | (20) |
Running this game through our Maple package, we obtain the following sequence of outputs. Due to the strong domination of pure strategy
Due to the strong domination of pure strategy 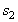 over
over 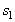 for Player 1 and pure strategy
for Player 1 and pure strategy 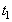 over
over 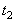 for Player 2, the pair
for Player 2, the pair 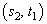 is the only Nash equilibrium and this equilibrium pays out 2 to each player.
is the only Nash equilibrium and this equilibrium pays out 2 to each player.
4.1. The Job Market ([1], p. 130-131, 164-165)
This game was described in Section 1.1 and its bimatrix game is depicted by Eq. (1). We perform the analysis of the game in three steps.Case 1: Assume that 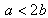 and
and 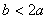 , that is, the two salaries are not too far out of line with each other. We run this game through our Maple package with the given constraints to obtain the following.
, that is, the two salaries are not too far out of line with each other. We run this game through our Maple package with the given constraints to obtain the following.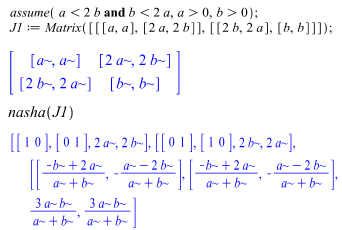 We see that in this case the game admits two Nash equilibria in pure strategies and one mixed strategy equilibrium. The pure Nash equilibria indicate that the two players are better off when they apply for distinct positions. To understand the meaning of the mixed Nash equilibrium, we take the example where a = $60,000 and b = $68,000. For this example, the mixed Nash equilibrium prescribes that both players apply to Firm 1 with probability 13/32 and to Firm 2 with probability 19/32. The expected payoff for each player from the use of this mixed strategy equilibrium is $95,625.Case 2: Assume that a > 2b, that is, Firm 1’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.
We see that in this case the game admits two Nash equilibria in pure strategies and one mixed strategy equilibrium. The pure Nash equilibria indicate that the two players are better off when they apply for distinct positions. To understand the meaning of the mixed Nash equilibrium, we take the example where a = $60,000 and b = $68,000. For this example, the mixed Nash equilibrium prescribes that both players apply to Firm 1 with probability 13/32 and to Firm 2 with probability 19/32. The expected payoff for each player from the use of this mixed strategy equilibrium is $95,625.Case 2: Assume that a > 2b, that is, Firm 1’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.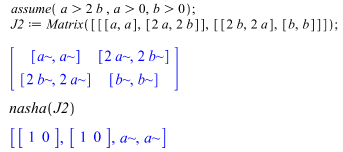 Note that due to the strong domination of pure strategy Firm 1 over Firm 2 for both players, the pair (Firm 1, Firm 1) is the only Nash equilibrium and this equilibrium pays out a to each player.Case 3: Assume that b > 2a, that is, Firm 2’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.
Note that due to the strong domination of pure strategy Firm 1 over Firm 2 for both players, the pair (Firm 1, Firm 1) is the only Nash equilibrium and this equilibrium pays out a to each player.Case 3: Assume that b > 2a, that is, Firm 2’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.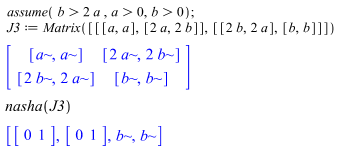 Note that this time pure strategy Firm 2 dominates strongly Firm 1 for both players. Therefore, the pair (Firm 2, Firm 2) is the only Nash equilibrium and this equilibrium pays out b to each player.
Note that this time pure strategy Firm 2 dominates strongly Firm 1 for both players. Therefore, the pair (Firm 2, Firm 2) is the only Nash equilibrium and this equilibrium pays out b to each player.
4.2. An Evolutionary Game ([2], p. 282-283)
This game was described in Section 1.1 and its bimatrix game is depicted by Eq. (2). We perform the analysis of the game in two steps. Case 1: a > b, that is, the territory is worth fighting for because the cost of the fight is low. We run this game through our Maple package with the given constraints on the parameters to obtain the following.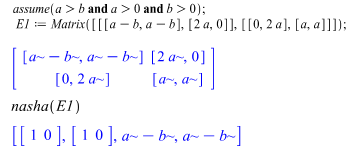 We observe that pure strategy Hawk strongly dominates pure strategy Dove. Hence, the pure strategy pair (Hawk, Hawk) is the only Nash equilibrium and this equilibrium pays out each player the territorial amount a – b.Case 2: a < b, that is, the territory is not worth fighting for because the cost of the fight is too high. A bird may win the fight but may not be able afterward to use the territory because of injury. This case is sometimes referred to as the nuclear option or the suicidal option. We run this game through our Maple package with the given constraints on the parameters to obtain the following.
We observe that pure strategy Hawk strongly dominates pure strategy Dove. Hence, the pure strategy pair (Hawk, Hawk) is the only Nash equilibrium and this equilibrium pays out each player the territorial amount a – b.Case 2: a < b, that is, the territory is not worth fighting for because the cost of the fight is too high. A bird may win the fight but may not be able afterward to use the territory because of injury. This case is sometimes referred to as the nuclear option or the suicidal option. We run this game through our Maple package with the given constraints on the parameters to obtain the following.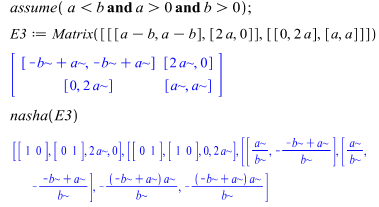 Maple yields three Nash equilibria of which two are pure strategy pairs, namely (Hawk, Dove) and (Dove, Hawk), and one is a mixed strategy pair. We note that the mixed strategy equilibrium becomes (Hawk, Hawk) when the cost of fighting is equal to the value of the territory, that is, when a = b.
Maple yields three Nash equilibria of which two are pure strategy pairs, namely (Hawk, Dove) and (Dove, Hawk), and one is a mixed strategy pair. We note that the mixed strategy equilibrium becomes (Hawk, Hawk) when the cost of fighting is equal to the value of the territory, that is, when a = b.
4.3. A Variant of the Game of Chicken ([1], p. 125-127)
This is a classic game in game theory and has some similarities with the Hawk-Dove game discussed in Section 4.2. When we input this game into our Maple package, we obtain the following.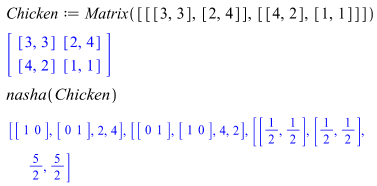 We see that there are two equilibria in pure strategies and there is a unique mixed strategy equilibrium where each player uses each of his or her pure strategies with equal probability. This mixed equilibrium pays out 5/2 to each player.
We see that there are two equilibria in pure strategies and there is a unique mixed strategy equilibrium where each player uses each of his or her pure strategies with equal probability. This mixed equilibrium pays out 5/2 to each player.
4.4. Prisoner’s Dilemma ([1], p. 125-127)
The Prisoner’s Dilemma is a type of non-zero-sum game in which two players may each “cooperate” (C) with each other or “defect” (D), that is, betray the other prisoner. This is a two-by-two game whose bimatrix game is given below. We run this game with our Maple package and we obtain the following.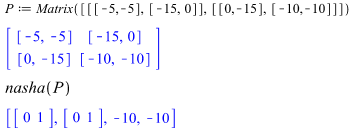 For both players pure strategy D strongly dominates pure strategy C. Hence (D, D) is the unique Nash equilibrium. Therefore, “defect” is the postulated non-cooperative outcome. However (C, C) provides a better payoff to both players. Therefore, non-cooperative selfish rationality conflicts with collective interest arguments. In Prisoner’s Dilemma, we observe that decentralizing the strategic choices has a high collective cost.
For both players pure strategy D strongly dominates pure strategy C. Hence (D, D) is the unique Nash equilibrium. Therefore, “defect” is the postulated non-cooperative outcome. However (C, C) provides a better payoff to both players. Therefore, non-cooperative selfish rationality conflicts with collective interest arguments. In Prisoner’s Dilemma, we observe that decentralizing the strategic choices has a high collective cost.
4.5. A Three-By-Four Game ([1], p. 129)
This is an example of a game that shows the limitation of our program. Our package can only identify the pure Nash equilibria of this game. This game admits two pure strategy Nash equilibria. But we should not be content with these Nash equilibria. The game may admit further Nash equilibria when mixed strategies are considered. In fact, since games typically have an odd number of Nash equilibria, there must be at least one mixed strategy Nash equilibrium. Unfortunately, mixed equilibrium computational capability of our program is limited to only two-player, two-strategy games.
This game admits two pure strategy Nash equilibria. But we should not be content with these Nash equilibria. The game may admit further Nash equilibria when mixed strategies are considered. In fact, since games typically have an odd number of Nash equilibria, there must be at least one mixed strategy Nash equilibrium. Unfortunately, mixed equilibrium computational capability of our program is limited to only two-player, two-strategy games.
5. Conclusions
We developed a Maple package for computing Nash equilibria of two-person non-cooperative games. The included illustrative examples show that the program performs well and successfully identifies the Nash equilibria of games whose payoffs are numerical as well as symbolic. At the moment, our program can compute the pure Nash equilibria of every two-person m-by-n game and the mixed Nash equilibria of any two-by-two game. Therefore, a short term goal of our research is to develop a program that is able to compute the pure and mixed Nash equilibria of every two-person m-by-n game. A long term goal is to develop a program that can identify the Nash equilibria of two-player two-strategy and three player-two strategy quantum games. The theory of quantum games for two-player, two-strategy and three-player, two-strategy is well-studied and some of its references can be found in [7], [8], and [9].
ACKNOWLEDGMENTS
This research was supported by the Texas A&M University – Kingsville’s Council for Undergraduate Research (TCUR).
References
| [1] | S. Stahl, A Gentle Introduction to Game Theory, the American Mathematical Society, 1999. |
| [2] | K. Binmore, Fun and Games, D. C. Heat Company, ISBN: 0-669-24603-4, 1991. |
| [3] | L. Bernardin etc, Maple Programming Guide, Waterloo Maple Inc, 2011. |
| [4] | J. Nash, Equilibrium Points in N-person Games, Proc. Natl. Acad. USA 36(1), 48-49, 1950. |
| [5] | A. Ahmed, Quantum Games and Quaternionic Strategies, Quantum Inf. Process. Springer, 12: 2701-2720, 2013. |
| [6] | A. Shaik and A. Ahmed, Best Response Analysis in Two-Person Quantum Games, APM 341-356, 2014. |
| [7] | A.O. Ahmed, Quaternions, Arbitrary Maximally Entangled States, and the Quantization of Two Player, Two Strategy Games, Proceedings to the 14th World Multi-Conference on Systemics, Cybernetics and Informatics, Vol. I, (2010) 376-380. |
| [8] | A. Ahmed, F.S. Khan, and S. A. Bleiler, The Octonionization of Three-Player, Two-Strategy Maximally Entangled Quantum Games, International Journal of Quantum Information, Vol. 8, No. 3 (2010) 411-434. |
| [9] | A. O. Ahmed, Equilibria in Quantum Three-Player Dilemma Game, British Journal of Mathematics & Computer Science, Science Domain International, (2013) 3(2):195-208. |

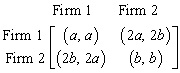
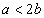 and
and 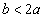 (the two salaries are not too far out of line with each other),
(the two salaries are not too far out of line with each other), 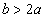 (Firm 2’s position pays very well), and
(Firm 2’s position pays very well), and 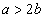 (Firm 1’s position pays very well), we will see that the nature of Nash equilibria will change from one case to the other. Note that numerical programs will not be helpful in solving this problem as the entries in the bimatrix game are all given as parameters. We will discuss the solution of this game in details in Section 4.
(Firm 1’s position pays very well), we will see that the nature of Nash equilibria will change from one case to the other. Note that numerical programs will not be helpful in solving this problem as the entries in the bimatrix game are all given as parameters. We will discuss the solution of this game in details in Section 4.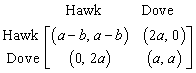
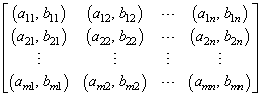
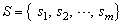 while Player 2 has at her disposal n pure strategies, namely
while Player 2 has at her disposal n pure strategies, namely 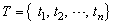 . The game is played as follows. Simultaneously, Player 1 chooses
. The game is played as follows. Simultaneously, Player 1 chooses 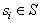 and Player 2 chooses
and Player 2 chooses 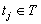 , each unaware of the choice of the other. Then their choices are made known and Player 1 wins the amount
, each unaware of the choice of the other. Then their choices are made known and Player 1 wins the amount 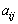 and Player 2 wins the amount
and Player 2 wins the amount 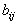 . This bimatrix can be broken up into two matrices A and B, the payoff matrices of Player 1 and Player 2, respectively, as shown below.
. This bimatrix can be broken up into two matrices A and B, the payoff matrices of Player 1 and Player 2, respectively, as shown below.
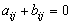 for all
for all 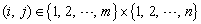 . It is constant-sum if
. It is constant-sum if 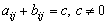 for all i and j. Otherwise, it is called a non-constant game.The main goal in game theory is the identification of some special strategic profiles. For example, given a fixed strategy t* ϵ T of the opponent, Player 1 would like to identify a best reply strategy, that is, a strategy s*ϵ S that delivers a utility at least as great than any other strategy s ϵ S. In symbols, this means that
for all i and j. Otherwise, it is called a non-constant game.The main goal in game theory is the identification of some special strategic profiles. For example, given a fixed strategy t* ϵ T of the opponent, Player 1 would like to identify a best reply strategy, that is, a strategy s*ϵ S that delivers a utility at least as great than any other strategy s ϵ S. In symbols, this means that 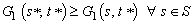 , where the payoff functions G1 and G2 are defined as
, where the payoff functions G1 and G2 are defined as 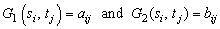 .The situation when both players have chosen such a strategy is of fundamental importance in game theory and described by the following definition.
.The situation when both players have chosen such a strategy is of fundamental importance in game theory and described by the following definition. 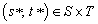 such that
such that 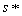 is a best reply to
is a best reply to 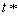 and
and 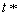 is a best reply to
is a best reply to 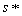 . In symbols,
. In symbols, 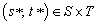 is a Nash equilibrium in G if and only if
is a Nash equilibrium in G if and only if 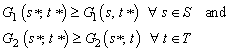
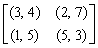
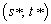 such that
such that 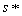 is a best reply to
is a best reply to 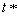 and
and 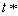 is a best reply to
is a best reply to 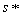 . Therefore, this game admits no Nash equilibria in pure strategies. Fortunately, game theorists usually extend the game G by enlarging the domain and extending the payoff functions. A standard extension of this point is to consider for each player the set of mixed strategies, that is, the sets of probability distributions over S and T. If X is a nonempty finite set, say.X = {x1, x2, …, xn}, we denote the probability distributions over X by
. Therefore, this game admits no Nash equilibria in pure strategies. Fortunately, game theorists usually extend the game G by enlarging the domain and extending the payoff functions. A standard extension of this point is to consider for each player the set of mixed strategies, that is, the sets of probability distributions over S and T. If X is a nonempty finite set, say.X = {x1, x2, …, xn}, we denote the probability distributions over X by 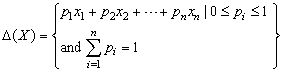
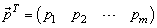
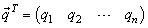
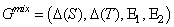 , where
, where 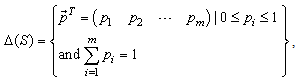
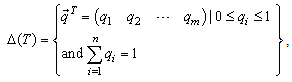
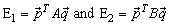 are the expected payoffs to Player 1 and Player 2, respectively.Note that the game Gmix contains the game G.Nash’s Theorem [4] says that if S and T are finite as above, then there always exists at least one equilibrium in Gmix. Note that every equilibrium in G is also an equilibrium in Gmix. Hence, throughout, we will only look for the equilibria in the mixed game as they also include the equilibria of G.
are the expected payoffs to Player 1 and Player 2, respectively.Note that the game Gmix contains the game G.Nash’s Theorem [4] says that if S and T are finite as above, then there always exists at least one equilibrium in Gmix. Note that every equilibrium in G is also an equilibrium in Gmix. Hence, throughout, we will only look for the equilibria in the mixed game as they also include the equilibria of G.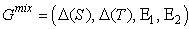 be its associated mixed game. A mixed Nash equilibrium (MNE) for Gmix is a strategy profile
be its associated mixed game. A mixed Nash equilibrium (MNE) for Gmix is a strategy profile 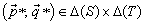 such that
such that 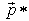 is a best reply to
is a best reply to 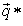 and
and 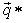 is a best reply to
is a best reply to 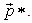 In symbols,
In symbols, 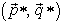 is a Nash equilibrium in Gmix if and only if
is a Nash equilibrium in Gmix if and only if 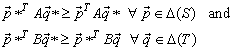
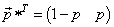 and
and 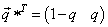 , it is an easy exercise to show that
, it is an easy exercise to show that 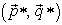 is a Nash equilibrium if and only if
is a Nash equilibrium if and only if 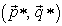 is a solution of the linear programming problem
is a solution of the linear programming problem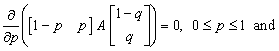
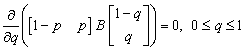 We develop a Maple procedure called nashp that produces all pure Nash equilibria of all m×n matrix games. The Maple codes in this procedure are directly based on the definition of pure Nash equilibrium. In contrast, to identify the mixed Nash equilibria of 2×2 games, the Maple procedure which we call nashm will be used. The structure of this procedure is based on solving linear equations and inequalities which are related to the payoff matrices.Let G = (S, T, A, B) be a two-person, two-strategy non-cooperative game, that is, both sets S and T contains each exactly two elements. Let
We develop a Maple procedure called nashp that produces all pure Nash equilibria of all m×n matrix games. The Maple codes in this procedure are directly based on the definition of pure Nash equilibrium. In contrast, to identify the mixed Nash equilibria of 2×2 games, the Maple procedure which we call nashm will be used. The structure of this procedure is based on solving linear equations and inequalities which are related to the payoff matrices.Let G = (S, T, A, B) be a two-person, two-strategy non-cooperative game, that is, both sets S and T contains each exactly two elements. Let 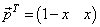 and
and 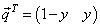 be Player 1 and Player 2 mixed strategies, respectively. Then, the Maple command solve is utilized to solve linear systems of equations subject to inequalities. The system with constraints
be Player 1 and Player 2 mixed strategies, respectively. Then, the Maple command solve is utilized to solve linear systems of equations subject to inequalities. The system with constraints 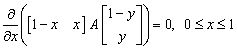
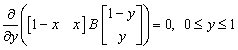

 The following command makes the package work in Maple.Savelib (nashe);The input of every procedure in the package is a bimatrix, that is, a matrix whose entries are ordered pairs of real numbers. In each pair, the first number is Player 1’s payoff and the second number is Player 2’s payoff. For example, if the payoff matrix for Player 1 is given by
The following command makes the package work in Maple.Savelib (nashe);The input of every procedure in the package is a bimatrix, that is, a matrix whose entries are ordered pairs of real numbers. In each pair, the first number is Player 1’s payoff and the second number is Player 2’s payoff. For example, if the payoff matrix for Player 1 is given by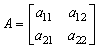
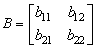
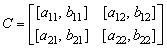
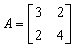 and
and 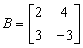 are the payoff matrices to Player 1 and Player 2, respectively, then the input matrix may be typed into Maple asC:=Matrix([[[3, 2], [2, 4]], [[2, 3], [4, – 3]]])In order to use a procedure, say nasha, one needs to type only once with (nashe) and nasha(C). Of course, one will need to press the Enter key in order to have each Maple command executed. The output of a procedure is a set of Nash equilibria followed by their corresponding payoffs. For example, a Nash equilibrium output has the following format.[ [Player 1’s optimal strategy], [Plyer 2’s optimal strategy], payoff for Player 1, Payoff for Player 2]
are the payoff matrices to Player 1 and Player 2, respectively, then the input matrix may be typed into Maple asC:=Matrix([[[3, 2], [2, 4]], [[2, 3], [4, – 3]]])In order to use a procedure, say nasha, one needs to type only once with (nashe) and nasha(C). Of course, one will need to press the Enter key in order to have each Maple command executed. The output of a procedure is a set of Nash equilibria followed by their corresponding payoffs. For example, a Nash equilibrium output has the following format.[ [Player 1’s optimal strategy], [Plyer 2’s optimal strategy], payoff for Player 1, Payoff for Player 2]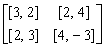
 This game has no equilibria in pure strategies. However, the game admits a unique equilibrium in mixed strategies where Player 1 uses his first and second pure strategies with probabilities 3/4 and 1/4, respectively, and Player 2 uses her first and second pure strategies with probabilities 2/3 and 1/3, respectively. This mixed strategy equilibrium pays out 8/3 to Player 1 and 9/4 to Player 2.Our second example is also a game taken from [1], p. 160-162 with bimatrix game given by
This game has no equilibria in pure strategies. However, the game admits a unique equilibrium in mixed strategies where Player 1 uses his first and second pure strategies with probabilities 3/4 and 1/4, respectively, and Player 2 uses her first and second pure strategies with probabilities 2/3 and 1/3, respectively. This mixed strategy equilibrium pays out 8/3 to Player 1 and 9/4 to Player 2.Our second example is also a game taken from [1], p. 160-162 with bimatrix game given by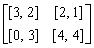
 This game admits two Nash equilibria in pure strategies, namely,
This game admits two Nash equilibria in pure strategies, namely, 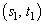 and
and 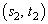 and the corresponding payoffs to the players are (3, 2) and (4, 4), respectively. There is a unique mixed strategy equilibrium where Player 1 employs each of his pure strategies with equal probability and Player 2 uses her first and second pure strategies with probabilities 2/5 and 3/5, respectively. This mixed strategy equilibrium pays out 12/5 to Player 1 and 5/2 to Player 2.Our third example is also a game taken from [1], p. 162-163 with bimatrix game given by
and the corresponding payoffs to the players are (3, 2) and (4, 4), respectively. There is a unique mixed strategy equilibrium where Player 1 employs each of his pure strategies with equal probability and Player 2 uses her first and second pure strategies with probabilities 2/5 and 3/5, respectively. This mixed strategy equilibrium pays out 12/5 to Player 1 and 5/2 to Player 2.Our third example is also a game taken from [1], p. 162-163 with bimatrix game given by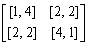
 Due to the strong domination of pure strategy
Due to the strong domination of pure strategy 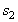 over
over 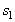 for Player 1 and pure strategy
for Player 1 and pure strategy 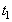 over
over 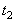 for Player 2, the pair
for Player 2, the pair 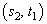 is the only Nash equilibrium and this equilibrium pays out 2 to each player.
is the only Nash equilibrium and this equilibrium pays out 2 to each player.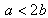 and
and 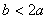 , that is, the two salaries are not too far out of line with each other. We run this game through our Maple package with the given constraints to obtain the following.
, that is, the two salaries are not too far out of line with each other. We run this game through our Maple package with the given constraints to obtain the following.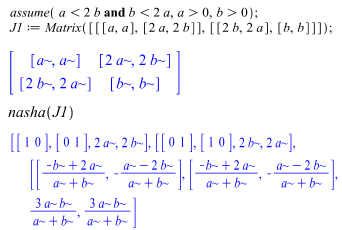 We see that in this case the game admits two Nash equilibria in pure strategies and one mixed strategy equilibrium. The pure Nash equilibria indicate that the two players are better off when they apply for distinct positions. To understand the meaning of the mixed Nash equilibrium, we take the example where a = $60,000 and b = $68,000. For this example, the mixed Nash equilibrium prescribes that both players apply to Firm 1 with probability 13/32 and to Firm 2 with probability 19/32. The expected payoff for each player from the use of this mixed strategy equilibrium is $95,625.Case 2: Assume that a > 2b, that is, Firm 1’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.
We see that in this case the game admits two Nash equilibria in pure strategies and one mixed strategy equilibrium. The pure Nash equilibria indicate that the two players are better off when they apply for distinct positions. To understand the meaning of the mixed Nash equilibrium, we take the example where a = $60,000 and b = $68,000. For this example, the mixed Nash equilibrium prescribes that both players apply to Firm 1 with probability 13/32 and to Firm 2 with probability 19/32. The expected payoff for each player from the use of this mixed strategy equilibrium is $95,625.Case 2: Assume that a > 2b, that is, Firm 1’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.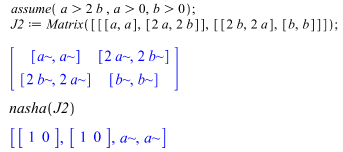 Note that due to the strong domination of pure strategy Firm 1 over Firm 2 for both players, the pair (Firm 1, Firm 1) is the only Nash equilibrium and this equilibrium pays out a to each player.Case 3: Assume that b > 2a, that is, Firm 2’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.
Note that due to the strong domination of pure strategy Firm 1 over Firm 2 for both players, the pair (Firm 1, Firm 1) is the only Nash equilibrium and this equilibrium pays out a to each player.Case 3: Assume that b > 2a, that is, Firm 2’s position pays very well when the two salaries are compared. We run this game through our Maple package with the given constraints and Maple yields the following.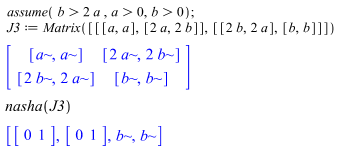 Note that this time pure strategy Firm 2 dominates strongly Firm 1 for both players. Therefore, the pair (Firm 2, Firm 2) is the only Nash equilibrium and this equilibrium pays out b to each player.
Note that this time pure strategy Firm 2 dominates strongly Firm 1 for both players. Therefore, the pair (Firm 2, Firm 2) is the only Nash equilibrium and this equilibrium pays out b to each player.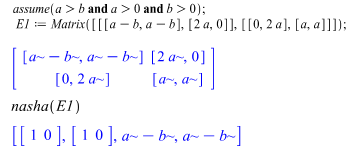 We observe that pure strategy Hawk strongly dominates pure strategy Dove. Hence, the pure strategy pair (Hawk, Hawk) is the only Nash equilibrium and this equilibrium pays out each player the territorial amount a – b.Case 2: a < b, that is, the territory is not worth fighting for because the cost of the fight is too high. A bird may win the fight but may not be able afterward to use the territory because of injury. This case is sometimes referred to as the nuclear option or the suicidal option. We run this game through our Maple package with the given constraints on the parameters to obtain the following.
We observe that pure strategy Hawk strongly dominates pure strategy Dove. Hence, the pure strategy pair (Hawk, Hawk) is the only Nash equilibrium and this equilibrium pays out each player the territorial amount a – b.Case 2: a < b, that is, the territory is not worth fighting for because the cost of the fight is too high. A bird may win the fight but may not be able afterward to use the territory because of injury. This case is sometimes referred to as the nuclear option or the suicidal option. We run this game through our Maple package with the given constraints on the parameters to obtain the following.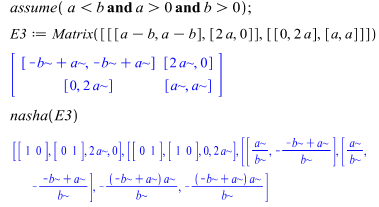 Maple yields three Nash equilibria of which two are pure strategy pairs, namely (Hawk, Dove) and (Dove, Hawk), and one is a mixed strategy pair. We note that the mixed strategy equilibrium becomes (Hawk, Hawk) when the cost of fighting is equal to the value of the territory, that is, when a = b.
Maple yields three Nash equilibria of which two are pure strategy pairs, namely (Hawk, Dove) and (Dove, Hawk), and one is a mixed strategy pair. We note that the mixed strategy equilibrium becomes (Hawk, Hawk) when the cost of fighting is equal to the value of the territory, that is, when a = b.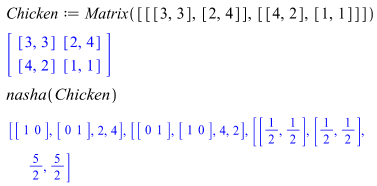 We see that there are two equilibria in pure strategies and there is a unique mixed strategy equilibrium where each player uses each of his or her pure strategies with equal probability. This mixed equilibrium pays out 5/2 to each player.
We see that there are two equilibria in pure strategies and there is a unique mixed strategy equilibrium where each player uses each of his or her pure strategies with equal probability. This mixed equilibrium pays out 5/2 to each player.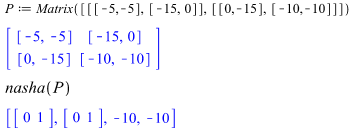 For both players pure strategy D strongly dominates pure strategy C. Hence (D, D) is the unique Nash equilibrium. Therefore, “defect” is the postulated non-cooperative outcome. However (C, C) provides a better payoff to both players. Therefore, non-cooperative selfish rationality conflicts with collective interest arguments. In Prisoner’s Dilemma, we observe that decentralizing the strategic choices has a high collective cost.
For both players pure strategy D strongly dominates pure strategy C. Hence (D, D) is the unique Nash equilibrium. Therefore, “defect” is the postulated non-cooperative outcome. However (C, C) provides a better payoff to both players. Therefore, non-cooperative selfish rationality conflicts with collective interest arguments. In Prisoner’s Dilemma, we observe that decentralizing the strategic choices has a high collective cost. This game admits two pure strategy Nash equilibria. But we should not be content with these Nash equilibria. The game may admit further Nash equilibria when mixed strategies are considered. In fact, since games typically have an odd number of Nash equilibria, there must be at least one mixed strategy Nash equilibrium. Unfortunately, mixed equilibrium computational capability of our program is limited to only two-player, two-strategy games.
This game admits two pure strategy Nash equilibria. But we should not be content with these Nash equilibria. The game may admit further Nash equilibria when mixed strategies are considered. In fact, since games typically have an odd number of Nash equilibria, there must be at least one mixed strategy Nash equilibrium. Unfortunately, mixed equilibrium computational capability of our program is limited to only two-player, two-strategy games. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML