-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2015; 5(3): 67-79
doi:10.5923/j.ajcam.20150503.01
Numerical Modelling of Thermal Explosion of a Single Sodium Droplet with Generic Reaction Rate and Variable Thermal Conductivity
K. S. Adegbie, S. J. Emojevwe
Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria
Correspondence to: K. S. Adegbie, Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The problem of thermal explosion of a single sodium droplet is essential because of its extensive use as a coolant in the design of nuclear reactor facilities. Most of the problems arising from ignition or thermal explosion of liquid single sodium droplet are based on constant reaction rate and thermal conductivity respectively. The present study extends the previous problem to account for generic reaction rate and variable thermal conductivity with convective and radiative heat losses. The generic reaction rate and thermal conductivity are varied as non-linear functions of temperature, whereas the contribution of thermal radiation is based on the P-1 approximation for thermal radiation transfer. An extension of existing models is obtained which is non-linear initial value problem. The differential equation is not open to analytical solution due to its non-linearity and so we investigate its behaviour numerically, using a finite difference procedure based on a small step-size. Parametric studies are performed to investigate significant effects of thermo-physical parameters on critical temperature and explosion time of the single droplet for typical reaction rates such as Sensitized, Arrhenius and Bimolecular reaction rates. The results display via tables and graphs show that the inclusion variable thermal conductivity and heat loss mechanism cause significant delays in the explosion time and reduces the critical temperature whereas contribution of generic reaction rates allows study on sensitized and bimolecular reaction rates which were not considered in the previous studies.
Keywords: Sodium droplet, Critical temperature, Explosion time, Variable thermal conductivity, Generic reaction rates, Non-Linear problem
Cite this paper: K. S. Adegbie, S. J. Emojevwe, Numerical Modelling of Thermal Explosion of a Single Sodium Droplet with Generic Reaction Rate and Variable Thermal Conductivity, American Journal of Computational and Applied Mathematics , Vol. 5 No. 3, 2015, pp. 67-79. doi: 10.5923/j.ajcam.20150503.01.
1. Introduction
- Recent advancement in reactor design is focused on construct of sodium cooled fast reactor. The novel development is essential because liquid sodium has excellent thermo-physical properties which are responsible for its extensive use as a coolant in the design of nuclear reactor facilities. However, hazardously reaction can occur when liquid sodium droplet is exposed to air or water. The surface reaction is considered between
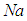 (subscript F) and
(subscript F) and 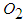 (subscript o), producing
(subscript o), producing 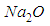 , according to
, according to 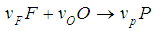 with generating heat
with generating heat 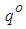 per unit mass of Na, where
per unit mass of Na, where 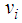 is the stoichiometric coefficient. For the safety of a sodium cooled fast reactor, sodium-air reactions should be prevented. To prevent and to mitigate the consequences, thermal explosion of sodium droplet, it is essential to understand various physical phenomena involved in a sodium-air reaction.Several researchers have delved into the problems of thermal explosion of combustible droplets in the literature. One of the utmost concerns is that of ignition of sodium droplet because of its extensive use as a working fluid in the design of nuclear facilities. Although basic research on droplet combustion has been conducted, some questions that arose from these previous studies (Makino, 2003; Makino, 2006; Makino and Fudaka, 2005; Alao et al., 2011) suggested the need for further investigations. Makino (2003) examined the theory and experimental comparisons of the ignition delay and limit of ignitability of a single sodium droplet. He concluded that, the ignitable range expand with increasing temperature and decreasing Nusselt number. Makino and Fudaka (2005) studied ignition and combustion of a single sodium droplet experimentally by using a falling droplet. It was established that the ignition delay time increases first gradually and then rapidly, with decreasing initial temperature and/or oxygen concentration and reached the limit of ignitability. In addition, Makino (2006) considered both theoretical and experimental analyses on ignition delay and limit of ignitability for sodium pool. In order to evaluate the appropriateness of the theory, experimental comparisons were conduced, using experimental data in the literature. It was demonstrated that there exists a fair degree of agreement between the experimental and analytical results, as far as the trend and approximate magnitude are concerned, in spite of difference in experimental conditions and several assumptions made in the analysis. Furthermore, it was found that an increase in the volume-to-surface-area ratio of the sodium pool prolongs ignition delay, and that a decrease in pool diameter suppresses ignition, both of which can be attributed to the reduced contribution of the surface reaction that supplies heat during the induction period. In another development, Alao et al. (2011) investigated the effect of thermal radiation on ignition time and critical temperature of a single sodium droplet. An extension of solutions of the existing model was obtained in the presence of radiative heat loss for ignition time and critical temperature by exploiting the sensitivity of the process to large chemical activation energy. Different qualitative effects of varying the dimensionless convective heat loss parameter with ignition time and critical temperature were observed. The results showed that the inclusion of additional heat sink mechanism, i.e. radiative heat loss, significantly delayed the ignition time and reduced the critical temperature with respect to results of Makino (2003). Adegbie (2013) extended the problem of thermal explosion in combustible gas mixtures containing fuel droplets to permit a more general temperature dependent rate of reaction for most typical practical reactions under physically reasonable assumptions. The analytical investigation provided explicit formulae for critical and transitional values of activation energy, gas temperature and intensity of combustion and evaporation with and without radiative heat loss. The results revealed that the existence of thermal radiation and numeric exponent play significant roles in the thermal stability of combustible gas mixture, which is of great importance for combustion and explosion industry safety. Goldfarb et al. (1999) performed the study of thermal radiation effect on thermal explosion in gas containing fuel droplets; they presented an original physical model of self-ignition in combustible gas mixture containing evaporating liquid droplets. The main attention of this paper was focused on the situation where delays might occur before final ignition. Goldfarb et al. (2004) studied the problem of delayed thermal explosion in a flammable gas mixture with addition of volatile fuel droplets based on the asymptotic method of integral manifolds. The model for the radiative heating of droplets used in this paper, took into account the semi-transparency of droplets, but it was assumed that gas in diesel engines is optically thick. This allowed the authors to assume that the radiation temperature is equal to gas temperature. A simplified model for droplet heat-up was used. The results of the analysis were applied to the modelling of thermal explosion in diesel engines. Goldfarb et al. (2007) investigated the dynamics of thermal explosion in a fuel droplets/air mixture using the geometrical version of the method of integral manifolds. The results were applied to the modelling of the ignition process in diesel engine. Effects of the thermal radiation, semi-transparency of droplets and oxidizer were taken into account. The relevant parametric regions of the system were analysed, and explicit analytical formulae for the ignition delay in the presence of thermal radiation were derived. It was shown that the effect of thermal radiation could lead to considerable reduction of the total ignition delay time. Okoya (2006) considered the effect of heat loss on the problem studied by Varatharajan and Williams (2000). Mostly analytical investigations of the simplified model using standard Semenov’ techniques were presented. The analytical method provided expressions for criticality and the transition points. Also, the different qualitative effects of varying the dimensionless parameters were investigated. Sazhin et al. (2001) considered thermal ignition analysis of a mono-disperse spray with radiation. The system of equations describing the effects of heating, evaporation, and combustion of fuel droplets in a mono-disperse spray was simplified assuming that the Nusselt and Sherwood numbers are equal to 2. The radiative energy exchange between fuel droplets surface and gas was described by using the P-1 model with Marshak boundary conditions. The chemical term was presented in the Arrhenius form with the pre-exponential factor calculated from the enthalpy equation, using the shell auto-ignition model. Sazhin (2006) reviewed recent developments in modelling the heating and evaporation of fuel droplets and identified unsolved problems. It was noted that modelling transient droplet heating using steady-state correlations for the convective heat transfer coefficient was misleading. At the initial stage of heating stationary droplets, the well known steady-state result Nu = 2 lead to under prediction of the rate of heating, while at the final stage the same result lead to over prediction. The numerical analysis of droplets heating using the effective thermal conductivity model was based on the analytical solution of the heat conduction equation inside the droplet. This approach was shown to have advantages compared with the approach based on the numerical solution of the same equation both from the point of view of accuracy and computer efficiency. Saravanan et al. (2012) investigated ignition behaviour of sodium droplets in the atmospheric air numerically with two available models of pre–ignition stage combustion. Analysis results showed that the reaction kinetics limited pre–ignition model predicts the limit of ignitability for sodium droplets under different initial and convective conditions, whereas the mass transfer limited pre–ignition model predicts this only under very low oxygen concentrations. Recently, Sathiah and Roelofs (2014) considered numerical modelling of single sodium droplet combustion. The model predictions of falling velocity and burned mass were in good agreement with experimental data. Additionally, parametric studies were performed to investigate the effects of initial droplet diameter, temperature and oxygen concentration on burning rate and on ignition time delay. In Okano and Yamaguchi (2003), a single sodium droplet combustion in steady-airflow was simulated using the COMET. Analyses on the spatial distributions of heat rate, temperature, formation, decomposition, and transfer of combustion products were performed. In addition, a free-falling droplet combustion experiment was simulated for code validation, where the evaluated falling-velocity and burnt-mass showed good agreement with the experimental values. Rao et al. (2012) analysed quasi-steady sodium droplet combustion in convective environment. The governing equations for mass, momentum, species and energy conservation were solved in axisymmetric cylindrical coordinates using the Finite Volume Method (FVM). The numerical model was validated with experimental results available in literature. Results for the fuel mass burning rates and flame shapes were presented for different sizes of droplets burning under different free-stream conditions. The model predicts the occurrence of envelope flame around a sodium droplet even at fairly high free-stream velocities.This present study extends the previous studies to account for generic reaction rate and variable thermal conductivity in the presence of convective and radiative heat losses, which none of the previous studies took into consideration. The resulting governing equation is highly non-linear ordinary differential equation. Consequently, a numerical technique known as a finite difference procedure based on a small step-size is employed to solve the governing equation due to its non-linearity. Parametric studies are performed to investigate the effects of thermo-physical parameters on temperature; explosion time and critical temperature of the single droplet for typical reaction rates such as Sensitized, Arrhenius and Bimolecular reaction rates.
is the stoichiometric coefficient. For the safety of a sodium cooled fast reactor, sodium-air reactions should be prevented. To prevent and to mitigate the consequences, thermal explosion of sodium droplet, it is essential to understand various physical phenomena involved in a sodium-air reaction.Several researchers have delved into the problems of thermal explosion of combustible droplets in the literature. One of the utmost concerns is that of ignition of sodium droplet because of its extensive use as a working fluid in the design of nuclear facilities. Although basic research on droplet combustion has been conducted, some questions that arose from these previous studies (Makino, 2003; Makino, 2006; Makino and Fudaka, 2005; Alao et al., 2011) suggested the need for further investigations. Makino (2003) examined the theory and experimental comparisons of the ignition delay and limit of ignitability of a single sodium droplet. He concluded that, the ignitable range expand with increasing temperature and decreasing Nusselt number. Makino and Fudaka (2005) studied ignition and combustion of a single sodium droplet experimentally by using a falling droplet. It was established that the ignition delay time increases first gradually and then rapidly, with decreasing initial temperature and/or oxygen concentration and reached the limit of ignitability. In addition, Makino (2006) considered both theoretical and experimental analyses on ignition delay and limit of ignitability for sodium pool. In order to evaluate the appropriateness of the theory, experimental comparisons were conduced, using experimental data in the literature. It was demonstrated that there exists a fair degree of agreement between the experimental and analytical results, as far as the trend and approximate magnitude are concerned, in spite of difference in experimental conditions and several assumptions made in the analysis. Furthermore, it was found that an increase in the volume-to-surface-area ratio of the sodium pool prolongs ignition delay, and that a decrease in pool diameter suppresses ignition, both of which can be attributed to the reduced contribution of the surface reaction that supplies heat during the induction period. In another development, Alao et al. (2011) investigated the effect of thermal radiation on ignition time and critical temperature of a single sodium droplet. An extension of solutions of the existing model was obtained in the presence of radiative heat loss for ignition time and critical temperature by exploiting the sensitivity of the process to large chemical activation energy. Different qualitative effects of varying the dimensionless convective heat loss parameter with ignition time and critical temperature were observed. The results showed that the inclusion of additional heat sink mechanism, i.e. radiative heat loss, significantly delayed the ignition time and reduced the critical temperature with respect to results of Makino (2003). Adegbie (2013) extended the problem of thermal explosion in combustible gas mixtures containing fuel droplets to permit a more general temperature dependent rate of reaction for most typical practical reactions under physically reasonable assumptions. The analytical investigation provided explicit formulae for critical and transitional values of activation energy, gas temperature and intensity of combustion and evaporation with and without radiative heat loss. The results revealed that the existence of thermal radiation and numeric exponent play significant roles in the thermal stability of combustible gas mixture, which is of great importance for combustion and explosion industry safety. Goldfarb et al. (1999) performed the study of thermal radiation effect on thermal explosion in gas containing fuel droplets; they presented an original physical model of self-ignition in combustible gas mixture containing evaporating liquid droplets. The main attention of this paper was focused on the situation where delays might occur before final ignition. Goldfarb et al. (2004) studied the problem of delayed thermal explosion in a flammable gas mixture with addition of volatile fuel droplets based on the asymptotic method of integral manifolds. The model for the radiative heating of droplets used in this paper, took into account the semi-transparency of droplets, but it was assumed that gas in diesel engines is optically thick. This allowed the authors to assume that the radiation temperature is equal to gas temperature. A simplified model for droplet heat-up was used. The results of the analysis were applied to the modelling of thermal explosion in diesel engines. Goldfarb et al. (2007) investigated the dynamics of thermal explosion in a fuel droplets/air mixture using the geometrical version of the method of integral manifolds. The results were applied to the modelling of the ignition process in diesel engine. Effects of the thermal radiation, semi-transparency of droplets and oxidizer were taken into account. The relevant parametric regions of the system were analysed, and explicit analytical formulae for the ignition delay in the presence of thermal radiation were derived. It was shown that the effect of thermal radiation could lead to considerable reduction of the total ignition delay time. Okoya (2006) considered the effect of heat loss on the problem studied by Varatharajan and Williams (2000). Mostly analytical investigations of the simplified model using standard Semenov’ techniques were presented. The analytical method provided expressions for criticality and the transition points. Also, the different qualitative effects of varying the dimensionless parameters were investigated. Sazhin et al. (2001) considered thermal ignition analysis of a mono-disperse spray with radiation. The system of equations describing the effects of heating, evaporation, and combustion of fuel droplets in a mono-disperse spray was simplified assuming that the Nusselt and Sherwood numbers are equal to 2. The radiative energy exchange between fuel droplets surface and gas was described by using the P-1 model with Marshak boundary conditions. The chemical term was presented in the Arrhenius form with the pre-exponential factor calculated from the enthalpy equation, using the shell auto-ignition model. Sazhin (2006) reviewed recent developments in modelling the heating and evaporation of fuel droplets and identified unsolved problems. It was noted that modelling transient droplet heating using steady-state correlations for the convective heat transfer coefficient was misleading. At the initial stage of heating stationary droplets, the well known steady-state result Nu = 2 lead to under prediction of the rate of heating, while at the final stage the same result lead to over prediction. The numerical analysis of droplets heating using the effective thermal conductivity model was based on the analytical solution of the heat conduction equation inside the droplet. This approach was shown to have advantages compared with the approach based on the numerical solution of the same equation both from the point of view of accuracy and computer efficiency. Saravanan et al. (2012) investigated ignition behaviour of sodium droplets in the atmospheric air numerically with two available models of pre–ignition stage combustion. Analysis results showed that the reaction kinetics limited pre–ignition model predicts the limit of ignitability for sodium droplets under different initial and convective conditions, whereas the mass transfer limited pre–ignition model predicts this only under very low oxygen concentrations. Recently, Sathiah and Roelofs (2014) considered numerical modelling of single sodium droplet combustion. The model predictions of falling velocity and burned mass were in good agreement with experimental data. Additionally, parametric studies were performed to investigate the effects of initial droplet diameter, temperature and oxygen concentration on burning rate and on ignition time delay. In Okano and Yamaguchi (2003), a single sodium droplet combustion in steady-airflow was simulated using the COMET. Analyses on the spatial distributions of heat rate, temperature, formation, decomposition, and transfer of combustion products were performed. In addition, a free-falling droplet combustion experiment was simulated for code validation, where the evaluated falling-velocity and burnt-mass showed good agreement with the experimental values. Rao et al. (2012) analysed quasi-steady sodium droplet combustion in convective environment. The governing equations for mass, momentum, species and energy conservation were solved in axisymmetric cylindrical coordinates using the Finite Volume Method (FVM). The numerical model was validated with experimental results available in literature. Results for the fuel mass burning rates and flame shapes were presented for different sizes of droplets burning under different free-stream conditions. The model predicts the occurrence of envelope flame around a sodium droplet even at fairly high free-stream velocities.This present study extends the previous studies to account for generic reaction rate and variable thermal conductivity in the presence of convective and radiative heat losses, which none of the previous studies took into consideration. The resulting governing equation is highly non-linear ordinary differential equation. Consequently, a numerical technique known as a finite difference procedure based on a small step-size is employed to solve the governing equation due to its non-linearity. Parametric studies are performed to investigate the effects of thermo-physical parameters on temperature; explosion time and critical temperature of the single droplet for typical reaction rates such as Sensitized, Arrhenius and Bimolecular reaction rates. 2. Mathematical Model
- Following the concept of previous models Makino (2003) and Alao et al. (2011), the present study addresses the problem of thermal explosion of a single sodium droplet taken into account generic reaction rate and variable thermal conductivity in the presence of convective and radiative heat losses. The contributions of the convective and radiative heat losses are based on Newton law of cooling and P-1 approximation for thermal radiation transfer respectively. The resulting governing equation is highly non-linear differential equation. It is pertinent to note that thermal conductivity of both monatomic and polyatomic gases is proportional to
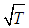 (see Adegbie (2008) and Adegbie (2013) for details). Therefore, in this study we assume thermal conductivity of sodium gas as non-linear function of temperature in the form
(see Adegbie (2008) and Adegbie (2013) for details). Therefore, in this study we assume thermal conductivity of sodium gas as non-linear function of temperature in the form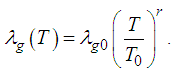 | (1) |
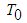 is initial temperature,
is initial temperature, 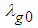 is thermal conductivity at initial temperature and
is thermal conductivity at initial temperature and 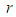 is numeric exponent. The contribution of convective heat loss is due to Newton law of cooling which is given as (see Adegbie (2013))
is numeric exponent. The contribution of convective heat loss is due to Newton law of cooling which is given as (see Adegbie (2013))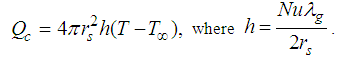 | (2) |
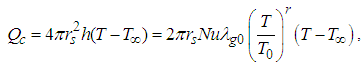 | (3) |
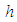 is the heat transfer coefficient, Nu is the Nusselt Number. Likewise, the radiative heat loss is given as (see Adegbie (2013) and Alao et al. (2011))
is the heat transfer coefficient, Nu is the Nusselt Number. Likewise, the radiative heat loss is given as (see Adegbie (2013) and Alao et al. (2011))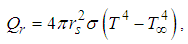 | (4) |
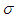 is the Stefan-Boltzmann’s constant.The pre-exponential factor is depicted by generic reaction rate, which is varied and only considered as non-linear function of temperature. Consequently, generic reaction rate is presented in the form (see Adegbie (2013) and Okoya (2006))
is the Stefan-Boltzmann’s constant.The pre-exponential factor is depicted by generic reaction rate, which is varied and only considered as non-linear function of temperature. Consequently, generic reaction rate is presented in the form (see Adegbie (2013) and Okoya (2006))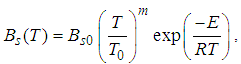 | (5) |
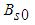 is pre-exponential factor at initial,
is pre-exponential factor at initial, 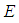 is the activation energy,
is the activation energy, 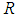 is the universal gas constant,
is the universal gas constant, 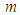 is the numeric exponent depicting typical reaction rate. Now, considering the concept of previous studies with inclusion of generic reaction rate and variable thermal conductivity (i.e. equations (3) and (5)) in the presence of convective and radiative heat losses, a more realistic model describing a single sodium droplet temperature is given in the form:
is the numeric exponent depicting typical reaction rate. Now, considering the concept of previous studies with inclusion of generic reaction rate and variable thermal conductivity (i.e. equations (3) and (5)) in the presence of convective and radiative heat losses, a more realistic model describing a single sodium droplet temperature is given in the form: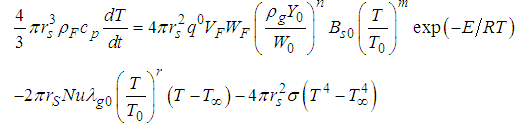 | (6) |
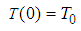 | (7) |
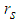 is the radius of single sodium droplet,
is the radius of single sodium droplet, 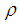 is the density,
is the density, 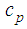 is the specific heat,
is the specific heat, 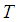 is the droplet temperature,
is the droplet temperature, 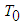 is the temperature in an oxidizing atmosphere with
is the temperature in an oxidizing atmosphere with 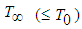 and oxygen mass fraction
and oxygen mass fraction 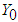 . t is the time,
. t is the time, 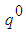 is the heat generated per unit mass of
is the heat generated per unit mass of 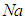 ,
, 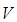 is the stoichiometric coefficient,
is the stoichiometric coefficient, 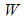 is the molecular weight,
is the molecular weight, 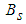 is the frequency factor of the “global” surface reaction with the activation energy
is the frequency factor of the “global” surface reaction with the activation energy 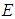 ,
, 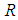 is the universal gas constant,
is the universal gas constant, 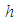 is the heat transfer coefficient,
is the heat transfer coefficient, 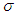 is the Stefan–Boltzman constant,
is the Stefan–Boltzman constant, 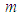 is the numeric exponent that depicts typical reaction rate,
is the numeric exponent that depicts typical reaction rate, 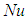 is the Nusselt number,
is the Nusselt number, 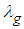 and
and 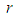 the thermal conductivity and its numeric exponent, and the subscripts
the thermal conductivity and its numeric exponent, and the subscripts 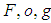 designate the fuel
designate the fuel 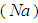 , ambient gas and oxygen respectively. Introduce the following dimensionless variables:
, ambient gas and oxygen respectively. Introduce the following dimensionless variables: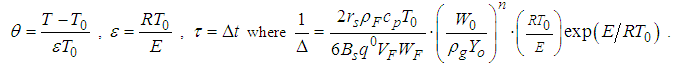 | (8) |
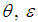 and
and 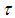 are dimensionless temperature, reduced activation energy and time respectively. At present, we obtain dimensionless sodium droplet temperature of equations (6) and (7) in the form
are dimensionless temperature, reduced activation energy and time respectively. At present, we obtain dimensionless sodium droplet temperature of equations (6) and (7) in the form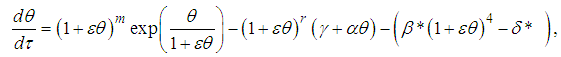 | (9) |
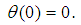 | (10) |
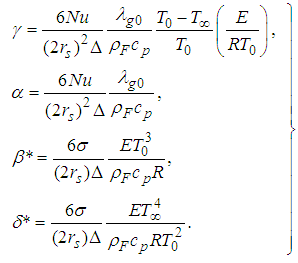 | (11) |
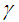 is convective heat loss parameters,
is convective heat loss parameters,  is the heat loss parameter via thermal conductivity,
is the heat loss parameter via thermal conductivity, 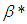 and
and 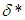 are modified parameters responsible for the contribution of the thermal radiation, Nusselt number
are modified parameters responsible for the contribution of the thermal radiation, Nusselt number 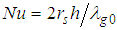 . In the limit of large activation energy (i.e.
. In the limit of large activation energy (i.e. 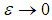 ), it is imperative to note that equation (9) without
), it is imperative to note that equation (9) without 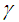 ,
, 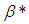 and
and 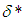 coincides with that of Semenov’s classical thermal explosion problem, Frank-Kamenetskii (1969). Whenever
coincides with that of Semenov’s classical thermal explosion problem, Frank-Kamenetskii (1969). Whenever 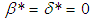 (i.e. radiative heat loss is neglected) and
(i.e. radiative heat loss is neglected) and 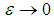 equation (9) is similar to the model in Makino (2003). Likewise, when
equation (9) is similar to the model in Makino (2003). Likewise, when 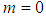 and
and 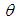 is asymptotically expanded to
is asymptotically expanded to 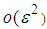 with constant thermal conductivity, we obtain equation (2.2) in Alao et al. (2011).
with constant thermal conductivity, we obtain equation (2.2) in Alao et al. (2011). 3. Numerical Computation
- The equations (9)-(10) arising from thermal explosion or ignition of a combustible single sodium droplet is non-linear initial value problem and does not possess closed form solutions. Therefore, we investigate thermal explosion behaviour of the model numerically using a finite difference procedure based on a small step-size. Consequently, parametric studies are performed from the numerical results obtained to investigate the effects of pertinent parameters on critical temperature, explosion time and temperature of the single sodium droplet as shown in Tables and Figures below.
4. Results
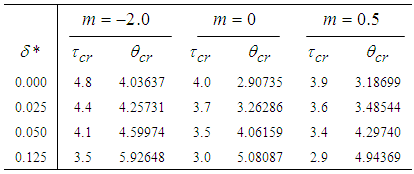
- The results in Tables 1-5 reveal the effects of major pertinent parameters on critical temperature and time for sensitized, Arrhenius and bimolecular reaction rates. It is worth noting that critical (or the lowest) temperature is the temperature below which the thermal explosion of a chemical reactant, including every gas-permeable oxidatively-heating substance, having arbitrary shape and an arbitrary size, placed in the atmosphere under isothermal conditions, cannot occur. This prevent hazardous event from happening in nuclear reactor facilities. In Table1, we observe a remarkable increment in critical temperature and a notable delay in time as reduced activation energy increases for typical sensitized, Arrhenius and bimolecular reaction rates. It is significant to note from Tables 2 and 3 that increase in convective heat loss parameters
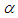 and
and 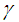 causes a notable reduction in the critical temperature whereas it notably causes delay in critical time for typical sensitized, Arrhenius and bimolecular reaction rates. Table 4 illustrates prominently reduction in critical temperature and delay in critical time as modified radiative heat loss parameter
causes a notable reduction in the critical temperature whereas it notably causes delay in critical time for typical sensitized, Arrhenius and bimolecular reaction rates. Table 4 illustrates prominently reduction in critical temperature and delay in critical time as modified radiative heat loss parameter 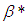 increases for typical sensitized, Arrhenius and bimolecular reaction rates. We notice in Table 5 that increase in modified radiative heat loss parameter
increases for typical sensitized, Arrhenius and bimolecular reaction rates. We notice in Table 5 that increase in modified radiative heat loss parameter 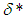 significantly raises critical temperature but it cause a drastic delay in critical time for typical sensitized, Arrhenius and bimolecular reaction rates.
significantly raises critical temperature but it cause a drastic delay in critical time for typical sensitized, Arrhenius and bimolecular reaction rates.
|
|
|
|
|
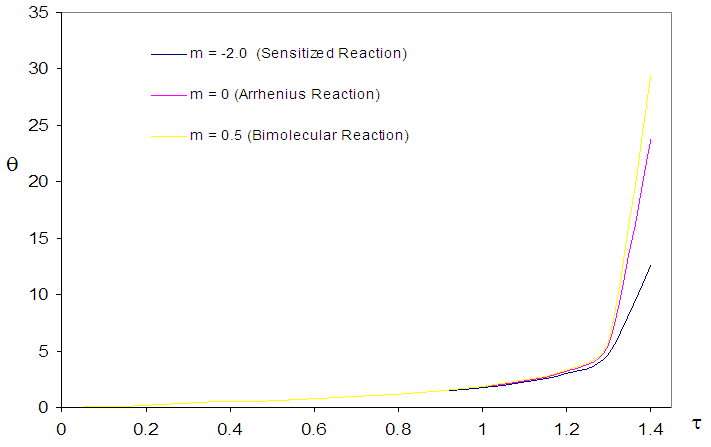 | Figure 1. Convectional thermal explosion of sodium droplet for typical reaction rates when 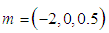 |
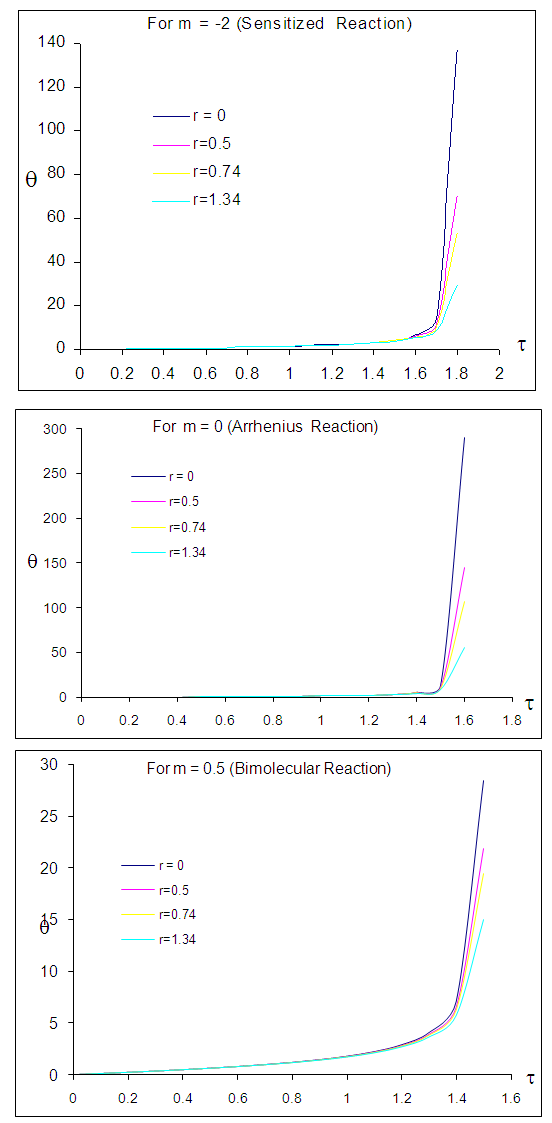 | Figure 2. Effects of numeric exponent 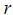 on thermal explosion of sodium droplet when on thermal explosion of sodium droplet when 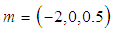 |
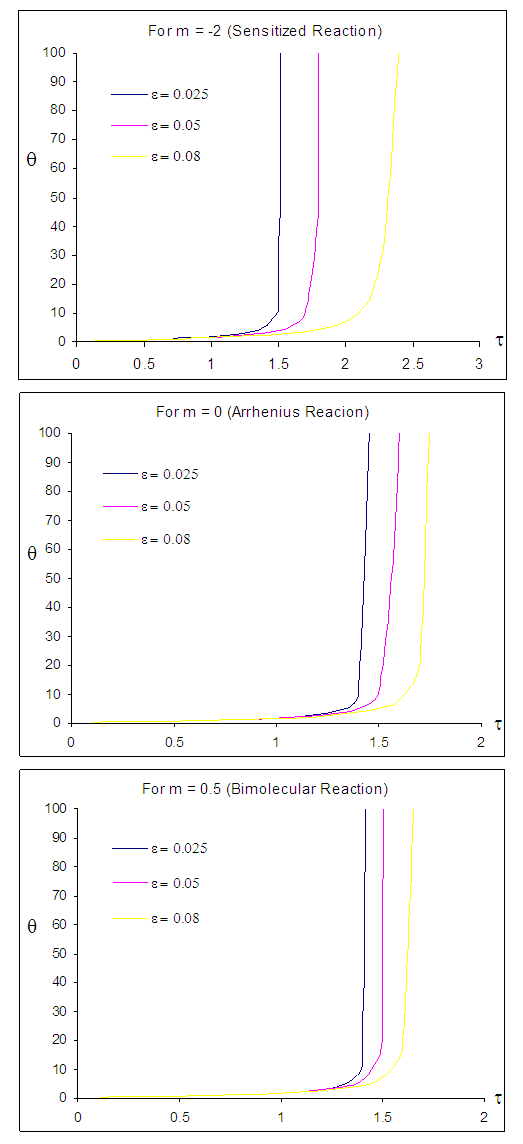 | Figure 3. Effects of reduced activation energy  on sodium droplet explosion time when on sodium droplet explosion time when 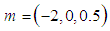 |
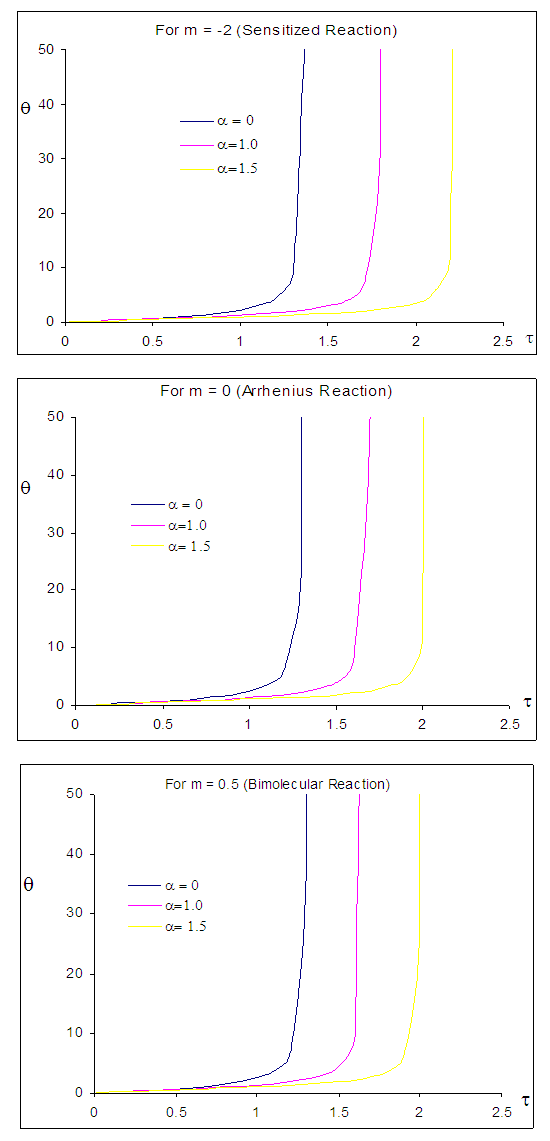 | Figure 4. Effects of convective heat loss parameter  on sodium droplet explosion time when on sodium droplet explosion time when  |
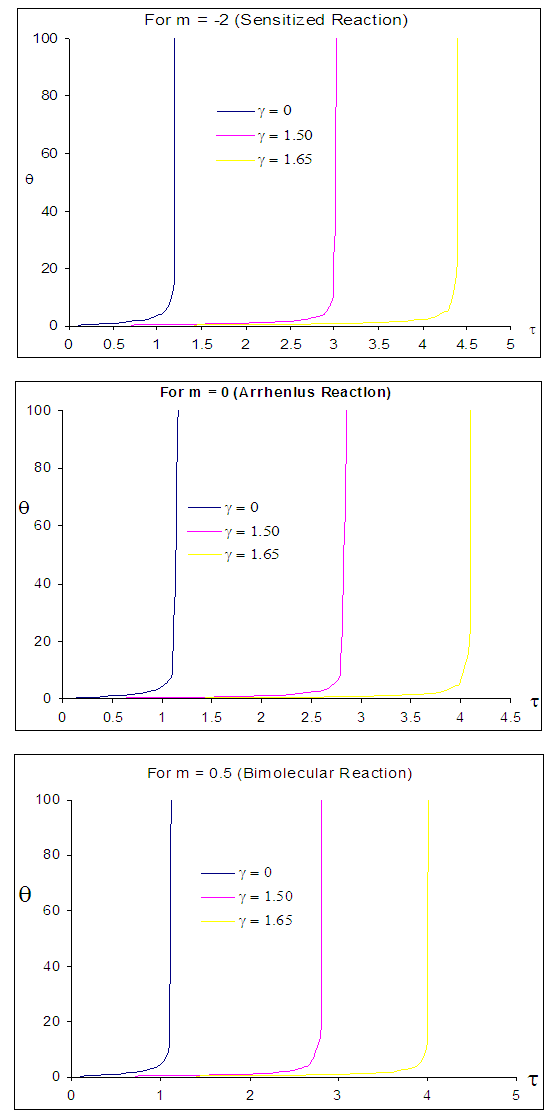 | Figure 5. Effects of convective heat loss parameter  on sodium droplet explosion time when on sodium droplet explosion time when  |
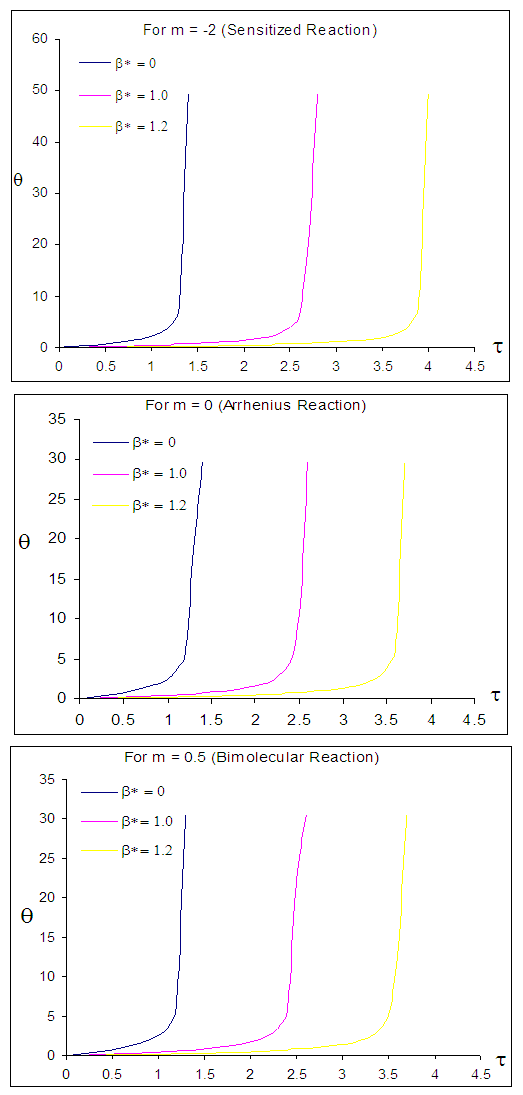 | Figure 6. Effects of radiative heat loss parameter 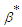 on sodium droplet explosion time when on sodium droplet explosion time when 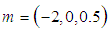 |
- The general characteristic features of Figures1-7 show the time histories of a combustible single sodium droplet. The sharp increase in combustible liquid single sodium droplet temperature indicates its explosive behaviour. Figures 1 and 2 show convectional thermal explosion of sodium droplet for typical sensitized, Arrhenius and bimolecular reaction rates. It pertinent to note that explosion occurs at the same time with different explosion temperature. In Fig.1, it is observed that increase in numeric exponent
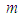 that depicts typical reaction rate significantly increases the explosion temperature whereas in Fig.2 the explosion temperature reduced drastically as numeric exponent
that depicts typical reaction rate significantly increases the explosion temperature whereas in Fig.2 the explosion temperature reduced drastically as numeric exponent 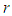 increases. Figure 3 illustrates the effects of reduced activation energy ε on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is observed that increase in reduced activation energy drastically causes delay in explosion time. Figure 4 corresponds to the effects of convective heat loss parameter
increases. Figure 3 illustrates the effects of reduced activation energy ε on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is observed that increase in reduced activation energy drastically causes delay in explosion time. Figure 4 corresponds to the effects of convective heat loss parameter 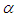 on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is obvious that increase in convective heat loss parameter
on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is obvious that increase in convective heat loss parameter 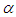 cause noticeable delay in sodium droplet explosion time. Likewise, Figure 5 describes the effects of convective heat loss parameter
cause noticeable delay in sodium droplet explosion time. Likewise, Figure 5 describes the effects of convective heat loss parameter 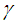 on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is worth noting that as convective heat loss parameter
on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is worth noting that as convective heat loss parameter 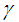 increases sodium droplet explosion time significantly increases. Figure 6 reveals the effects of modified radiative heat loss parameter
increases sodium droplet explosion time significantly increases. Figure 6 reveals the effects of modified radiative heat loss parameter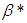 on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. Significant increment in sodium droplet explosion time is notice as modified radiative heat loss parameter
on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. Significant increment in sodium droplet explosion time is notice as modified radiative heat loss parameter 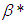 increases. In the same vein, Figure 7 shows the effects of modified radiative heat loss parameter
increases. In the same vein, Figure 7 shows the effects of modified radiative heat loss parameter 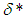 on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is observed that increase in modified radiative heat loss parameter
on sodium droplet explosion time for typical sensitized, Arrhenius and bimolecular reaction rates. It is observed that increase in modified radiative heat loss parameter 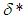 causes a significant reduction in sodium droplet explosion time.
causes a significant reduction in sodium droplet explosion time.5. Conclusions
- It is pertinent to note that previous studies on ignition or thermal explosion single sodium droplet were characterized only with constant reaction rate and thermal conductivity. In this study, the problems of thermal explosion of single sodium droplet have been extended to permit a more general reaction rates and variable thermal conductivity in the presence of both convective and radiative heat losses. The new model was considered under physically reasonable assumptions in order to obtain information which is useful for safety measures in nuclear reactor facilities. The mathematical formulation involves a highly non-linear ordinary differential equation. The entire dynamical picture of the model is qualitatively uncovered by exploiting numerical techniques. Numerical results were presented in Tables and Figures for sensitized, Arrhenius and bimolecular reaction rates respectively. The effects of varying pertinent dimensionless parameters were also reported. Tabular and graphical results revealed that the delay before explosion and reduction in critical temperature depend significantly on the inclusion of variable thermal conductivity and heat loss mechanisms, which is of great importance for nuclear facilities safety. In addition, contribution of generic reaction rates allows study on sensitized and bimolecular reaction rates which were not considered in the previous studies. Likewise, it is significant to note that the phenomenon of delay before the onset of explosion is very important from a practical point of view. The findings of this study are expected to trigger relevant safety measures in nuclear reactor facilities.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML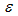 with critical temperature and time for sensitized, Arrhenius and Bimolecular reaction rates
with critical temperature and time for sensitized, Arrhenius and Bimolecular reaction rates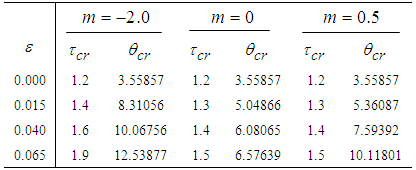
 with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates
with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates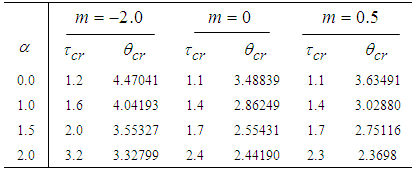
 with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates
with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates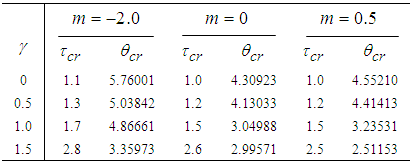
 with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates
with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates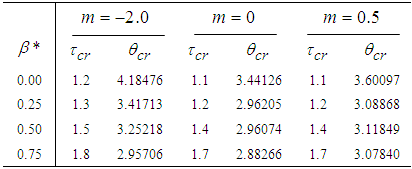
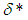 with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates
with critical temperature and time for Sensitized, Arrhenius and Bimolecular reaction rates