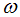-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2015; 5(2): 42-65
doi:10.5923/j.ajcam.20150502.03
Dengue in Tanzania - Vector Control and Vaccination
Laurencia Ndelamo Massawe1, Estomih S. Massawe2, Oluwole D. Makinde3
1Faculty of Science, Technology and Environmental Studies, The Open University of Tanzania, Dar es Salaam, Tanzania
2Mathematics Department, University of Dar es salaam, Dar es Salaam, Tanzania
3Faculty of Military Science, Stellenbosch University, Private Bag X2, Saldanha, South Africa
Correspondence to: Laurencia Ndelamo Massawe, Faculty of Science, Technology and Environmental Studies, The Open University of Tanzania, Dar es Salaam, Tanzania.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In this paper a mathematical model is presented to examine the effect of treatment, careful andCareless Susceptibles with control on the transmission of Dengue fever in the society. A nonlinear mathematical model for the problem is proposed and analysed quantitatively using the stability theory of the differential equations. The results show that the disease-free equilibrium point is locally and globally asymptotically stable if the reproduction number (R0) is less than unity. Then the endemic equilibrium is locally and globally asymptotically stable under certain conditions, using the additive compound matrices approach and Lyapunov method respectively. However treatment, careful Susceptibles and the control on the transmission of dengue fever disease will have a positive effect on decreasing the growth rate of dengue fever disease. The numerical simulation shows that on the application of vaccination, the number of infected individual is reduced.
Keywords: Dengue Fever Disease, treatment, Careful,Careless, Susceptible, Equilibrium, Control, infected, reproduction number, Vaccination
Cite this paper: Laurencia Ndelamo Massawe, Estomih S. Massawe, Oluwole D. Makinde, Dengue in Tanzania - Vector Control and Vaccination, American Journal of Computational and Applied Mathematics , Vol. 5 No. 2, 2015, pp. 42-65. doi: 10.5923/j.ajcam.20150502.03.
Article Outline
1. Introduction
- Dengue fever is a severe infection, flu-like illness transmitted to humans through the bites of infected female Aedes mosquitoes. Four different serotypes can cause dengue fever. A human infected by one serotype, on recovery, gains total immunity to that serotype and only partial and transient immunity with respect to the other three. Dengue fever can vary from mild to severe; the more severe forms of dengue fever include dengue hemorrhagic fever and dengue shock syndrome. Dengue hemorrhagic fever occurs when a person get infected by different type of dengue virus after being infected by another one sometimes before. Dengue shock syndrome is the most severe form of dengue infection. Dengue is found in tropical and sub-tropical climates worldwide, mostly in urban and semi-urban areas [1].Mathematical modelling of the population models continues to provide important insights into population behaviour and control. Over the years, it has also become an important tool in understanding the dynamics of diseases, and the decision making process regarding intervention programs for controlling population and disease problems in many countries [2].Mathematical modelling also became considerable important tool in the study of epidemiology because it helps in understanding the observed epidemiological patterns, disease control and provides understanding of the underlying mechanisms which influence the spread of disease and may suggest control strategies [1-8]. Moreover [9], presented a dynamical model that studied the temporal model for dengue disease with treatment. So far no research has considered a dynamical system that incorporates the control strategies to reduce the spread of the dengue fever disease through the campaign to educate the careless human susceptible, control vector human contact, removing vector breeding areas, insecticides application and control maturation rate from larvae to adult. In this work, we present an extension of the model of [9] to include temporary immunity, control strategies and Susceptibles with different behaviour i.e. the dynamical system that incorporates the effects Careful and Careless Susceptibles on the transmission of Dengue fever in the society with vaccination. In this paper, data reported by the ministry of health in Tanzania is used. In July 2010 for the first time in Dar es Salaam region -Tanzania, an outbreak of dengue fever was reported, over 40 people were infected and then also between May and July 2013,172 were infected with this disease. Moreover in the year 2014, the government of Tanzania announced the dangers of the disease in which people were alerted about the disease and the precaution to be taken. In this 2014, 399 people were infected in which 2 died of the disease in Dar es Salaam region (http://www.wavuti.com/2014/05/wizara-ya-afya-kitengo-cha.html). Data will be obtained from the different literature and estimated since there is no enough data in Tanzania. The purpose of this study is to match the empirical data with the modal simulation. Hence we formulate the SITRS (susceptible, Infected, Treated, Recovered, susceptible) and SVITRS (Susceptible, Vaccinated, Infected, Recovered, Susceptible) models for transmission of dengue fever disease.
2. Formulation of the Model
- In this section, we adopt the model presented in [10]. The model is based on two populations: humans and mosquitoes. Human population
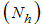 is divided into five groups such as
is divided into five groups such as 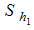 - Careful human Susceptibles,
- Careful human Susceptibles,  - Careless human Susceptibles,
- Careless human Susceptibles, 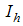 - infected human,
- infected human, 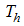 - treated infected human,
- treated infected human, 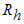 - recovery infected human, so that we have
- recovery infected human, so that we have 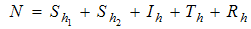 and the population of female mosquitoes, indexed by
and the population of female mosquitoes, indexed by 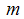 is divided into three groups that is
is divided into three groups that is 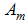 -Aquatic phase (that includes the egg, larva and pupa stages),
-Aquatic phase (that includes the egg, larva and pupa stages), 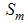 - Susceptibles (mosquitoes that are able to contract the disease),
- Susceptibles (mosquitoes that are able to contract the disease), 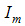 -Infectives (mosquitoes capable of transmitting the disease to human). In formulating the model, the following assumptions are considered:i. Total human population
-Infectives (mosquitoes capable of transmitting the disease to human). In formulating the model, the following assumptions are considered:i. Total human population 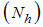 is constant,ii. The population is homogeneous, which means that every individual of a compartment is homogeneously mixed with the other individuals,iii. Immigration and emigration are not considered,iv. Each vector has an equal probability to bite any host,v. Humans and mosquitoes are assumed to be born susceptible i.e. there is no natural protection,vi. The coefficient of transmission of the disease is fixed and does not vary seasonally,vii. For the mosquito there is no resistant phase, due to its short lifetime,viii. The possibility of careless Susceptibles contracting dengue fever disease is higher than that for careful Susceptibles.Considering the above assumptions, we then have the following schematic model flow diagram for dengue fever disease with control:
is constant,ii. The population is homogeneous, which means that every individual of a compartment is homogeneously mixed with the other individuals,iii. Immigration and emigration are not considered,iv. Each vector has an equal probability to bite any host,v. Humans and mosquitoes are assumed to be born susceptible i.e. there is no natural protection,vi. The coefficient of transmission of the disease is fixed and does not vary seasonally,vii. For the mosquito there is no resistant phase, due to its short lifetime,viii. The possibility of careless Susceptibles contracting dengue fever disease is higher than that for careful Susceptibles.Considering the above assumptions, we then have the following schematic model flow diagram for dengue fever disease with control: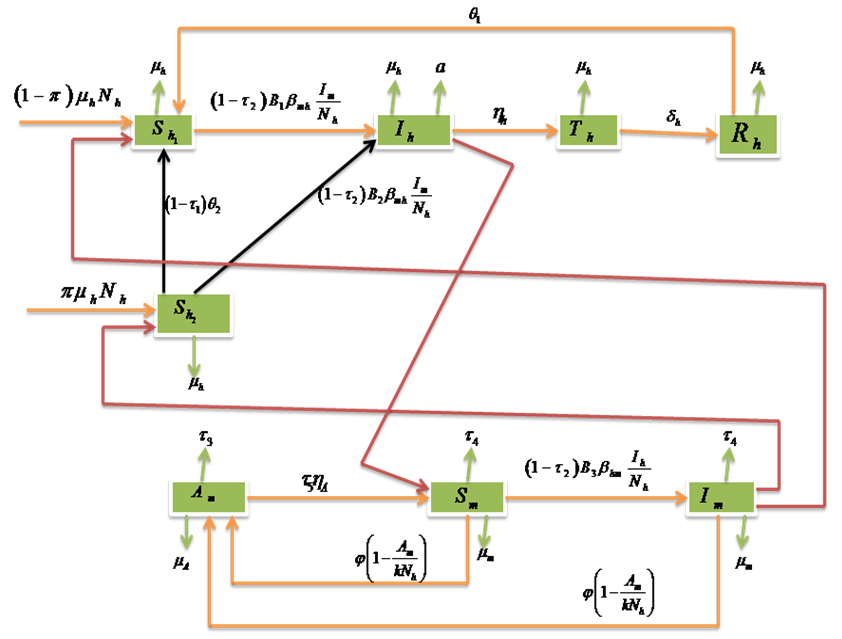 | Figure 1. Model Flow diagram for dengue fever disease with control |
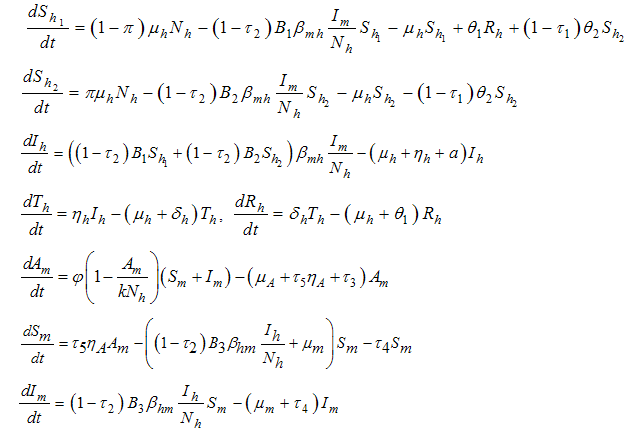 | (1) |
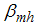 is the transmission probability from
is the transmission probability from 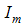 (per bite),
(per bite), 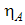 is the maturation rate from larvae to adult (per day),
is the maturation rate from larvae to adult (per day), 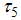 is the control maturation rate from larvae to adult,
is the control maturation rate from larvae to adult, 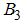 is the average daily biting (per day) for mosquito susceptible,
is the average daily biting (per day) for mosquito susceptible, 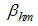 is the transmission probability from
is the transmission probability from 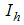 (per bite),
(per bite), 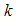 is the number of larvae per human,
is the number of larvae per human, 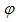 is the number of eggs at each deposit per capita (per day),
is the number of eggs at each deposit per capita (per day), 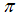 is the fraction of subpopulation recruited into the population,
is the fraction of subpopulation recruited into the population, 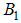 is the average daily biting (per day) for careful human susceptible,
is the average daily biting (per day) for careful human susceptible, 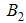 is the average daily biting (per day) for careless human susceptible,
is the average daily biting (per day) for careless human susceptible, 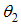 is the Positive change in behaviour of Careless individuals,
is the Positive change in behaviour of Careless individuals, 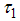 is the campaign of educating Careless human susceptible,
is the campaign of educating Careless human susceptible, 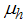 is the average lifespan of humans (per day),
is the average lifespan of humans (per day), 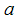 is the per capita disease induced death rate for humans,
is the per capita disease induced death rate for humans, 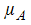 is the natural mortality of larvae (per day),
is the natural mortality of larvae (per day), 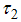 is the control of vector human contact ,
is the control of vector human contact , 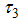 is the reducing vector breeding areas,
is the reducing vector breeding areas, 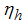 mean viremic period (per day),
mean viremic period (per day), 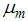 average lifespan of adult mosquitoes (per day),
average lifespan of adult mosquitoes (per day), 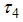 insecticide application,
insecticide application, 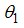 portion that moves from compartment
portion that moves from compartment 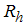 to
to 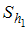 due to loss of immunity and
due to loss of immunity and 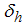 treatment parameter.
treatment parameter.3. Model Analysis
- We study the solutions of System (1) in the closed set
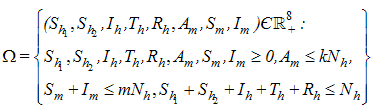 The set is positively invariant with respect to Equation (1) [10].
The set is positively invariant with respect to Equation (1) [10].3.1. Disease Free Equilibrium (DFE)
- For the disease free equilibrium, it is assumed that there is no infection for both populations of human and mosquitoes i.e.
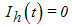 and
and 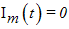 , denoted by
, denoted by 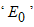 . Thus
. Thus 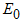 of the model system (1) is obtained as
of the model system (1) is obtained as 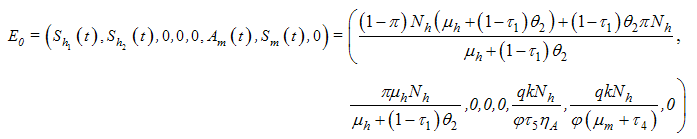 where
where 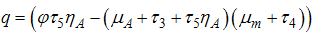
3.2. The Basic Reproduction Number, R0
- The basic reproduction number, denoted by
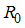 , is defined as the average number of secondary infections that occurs when one infective individual is introduced into a completely susceptible population [11].The basic reproduction number of the model (1)
, is defined as the average number of secondary infections that occurs when one infective individual is introduced into a completely susceptible population [11].The basic reproduction number of the model (1) 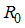 is calculated by using the next generation matrix of an ODE [11]. Using the approach of [11].
is calculated by using the next generation matrix of an ODE [11]. Using the approach of [11]. 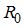 is obtaining by taking the largest (dominant) Eigen value (spectral radius) of
is obtaining by taking the largest (dominant) Eigen value (spectral radius) of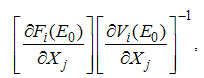 where,
where, 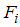 is the rate of appearance of new infection in compartment
is the rate of appearance of new infection in compartment 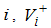 is the transfer of individuals out of the compartment
is the transfer of individuals out of the compartment 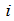 by all other means and
by all other means and 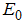 is the disease free equilibrium.
is the disease free equilibrium.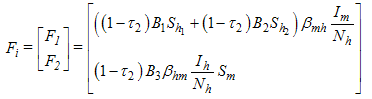 Using the linearization method, the associated matrix at DFE is given by
Using the linearization method, the associated matrix at DFE is given by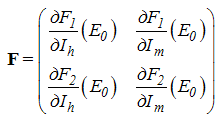 This implies that
This implies that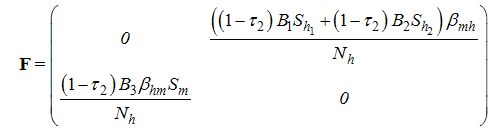 With
With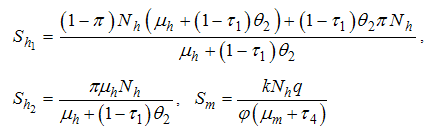 ,we have
,we have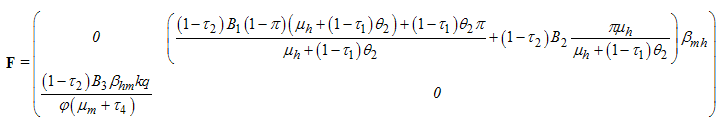 The transfer of individuals out of the compartment is given by
The transfer of individuals out of the compartment is given by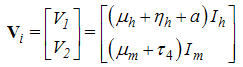 Using the linearization method, the associated matrix at DFE is given by,
Using the linearization method, the associated matrix at DFE is given by,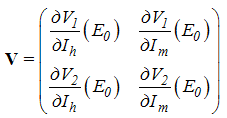 This gives
This gives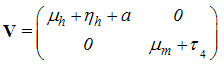 With
With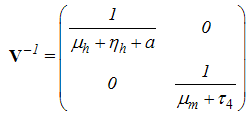 Therefore
Therefore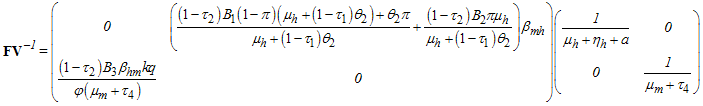 | (2) |
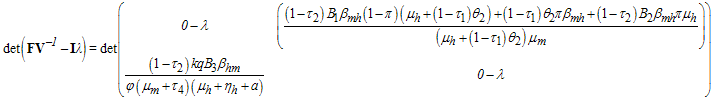 This gives
This gives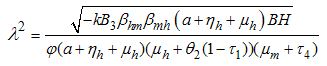 where
where 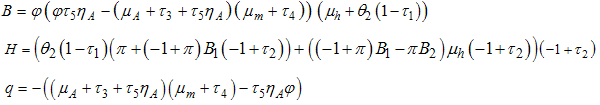 consequently
consequently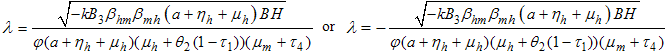 It follows that the Basic Reproductive number which is given by the largest Eigen value for model system (1) denoted by
It follows that the Basic Reproductive number which is given by the largest Eigen value for model system (1) denoted by 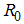 is given by
is given by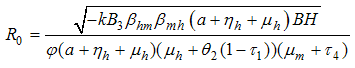 | (3) |
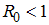 , the disease cannot invade the population and the infection will die out over a period of time, and also, if
, the disease cannot invade the population and the infection will die out over a period of time, and also, if 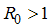 , then an invasion is possible and infection can spread through the population. Generally, the larger the value of
, then an invasion is possible and infection can spread through the population. Generally, the larger the value of 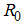 , the more severe, and possibly widespread the epidemic will be, [10].
, the more severe, and possibly widespread the epidemic will be, [10].3.3. Local Stability of Disease Free Equilibrium Point
- To determine the local stability of the disease free equilibrium, the variation matrix
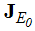 of the model system (1) corresponding to the disease free
of the model system (1) corresponding to the disease free 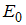 is obtained as
is obtained as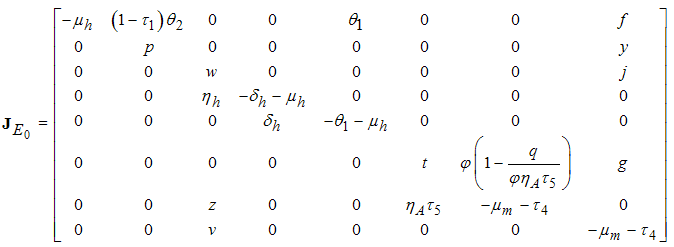 | (4) |
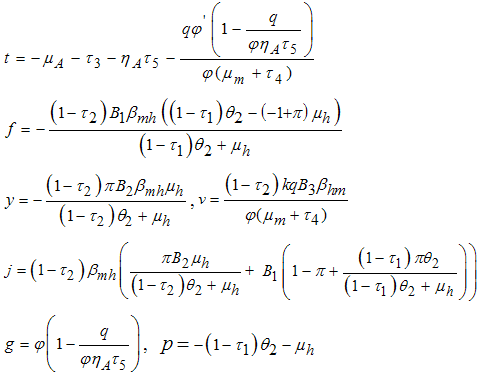
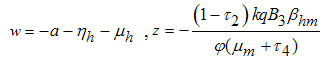 Therefore the stability of the disease free equilibrium point can be clarified by studying the behaviour of
Therefore the stability of the disease free equilibrium point can be clarified by studying the behaviour of  in which for local stability of DFE we seek for its all eigenvalues to have negative real parts. It follows that, the characteristic function of the matrix (4) with
in which for local stability of DFE we seek for its all eigenvalues to have negative real parts. It follows that, the characteristic function of the matrix (4) with 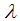 being the eigenvalues of the Jacobian matrix, by using Mathematica software gives the following values:
being the eigenvalues of the Jacobian matrix, by using Mathematica software gives the following values: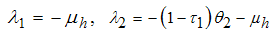 The other eigenvalues are given as
The other eigenvalues are given as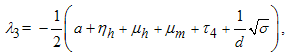 when
when 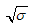 is not a real number,
is not a real number,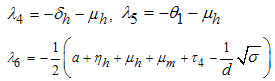 when
when 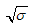 is not a real number,
is not a real number,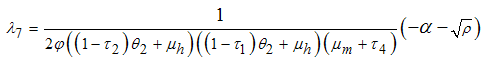 when
when 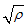 is not a real number, and finally.
is not a real number, and finally.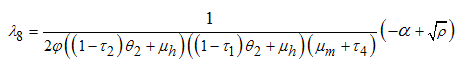 when
when 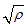 is not a real number, where
is not a real number, where 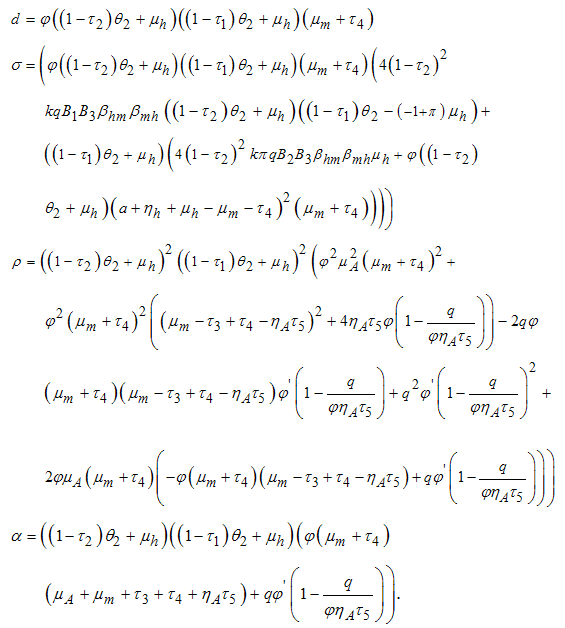 Hence under certain conditions the system is stable since all the eight eigenvalues are negative. These imply that at
Hence under certain conditions the system is stable since all the eight eigenvalues are negative. These imply that at 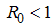 the Disease Free Equilibrium point is locally asymptotically stable.
the Disease Free Equilibrium point is locally asymptotically stable.3.4. Global Stability of Disease Free Equilibrium Point
- In this subsection, the global behaviour of the equilibria for system (1) is analysed. The following theorem provides the global property of the disease free equilibrium
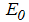 of the system. The results are obtained by means of Lyapunov function. In choosing the Lyapunov function, we adopt the idea of [12].Theorem1: If
of the system. The results are obtained by means of Lyapunov function. In choosing the Lyapunov function, we adopt the idea of [12].Theorem1: If 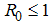 , then the infection-free equilibrium is globally asymptotically stable in the interior of
, then the infection-free equilibrium is globally asymptotically stable in the interior of  .Proof: To establish the global stability of the disease-free equilibrium, we construct the following Lyapunov function:
.Proof: To establish the global stability of the disease-free equilibrium, we construct the following Lyapunov function: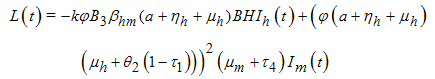 | (5) |
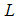 along (4), we obtain
along (4), we obtain 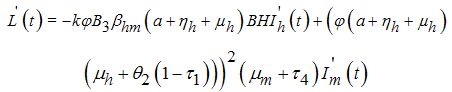 Then substituting
Then substituting 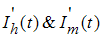 from system (1), we get
from system (1), we get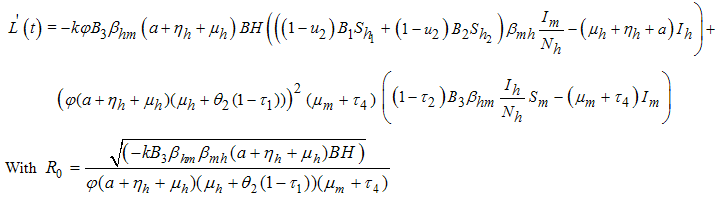 it follows that
it follows that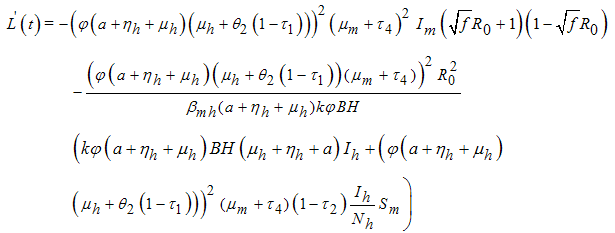 where
where 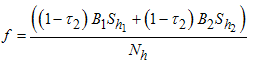 Thus,
Thus, 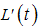 is negative if
is negative if 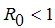 and
and 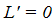 if and only if
if and only if 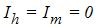 is reduced to the DFE. Consequently, the largest compact invariant set in
is reduced to the DFE. Consequently, the largest compact invariant set in 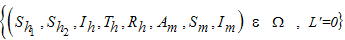 when
when 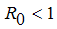 is the singleton
is the singleton 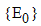 . Hence, by LaSalle’s invariance principle, it is implied that
. Hence, by LaSalle’s invariance principle, it is implied that 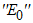 is globally asymptotically stable in Ω [13]. This completes the proof.
is globally asymptotically stable in Ω [13]. This completes the proof.3.5. Existence of Local and Global Asymptotic Stability of Endemic Equilibrium
- Since we are dealing with presence of dengue fever disease in human population, we can reduce system (1) to a 4-dimensional system by eliminating
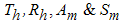 respectively, in the feasible region
respectively, in the feasible region 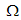 . The values of
. The values of 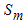 can be determined by setting
can be determined by setting 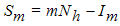 to obtain
to obtain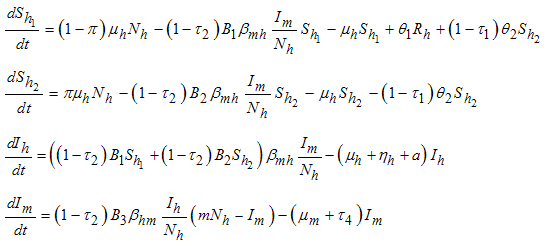 | (6) |
3.5.1. The Endemic Equilibrium and Its Stability
- Here, we study the existence and stability of the endemic equilibrium points. If
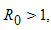 then the host-vector model system (6) has a unique endemic equilibrium given by
then the host-vector model system (6) has a unique endemic equilibrium given by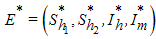 in
in 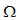 , with
, with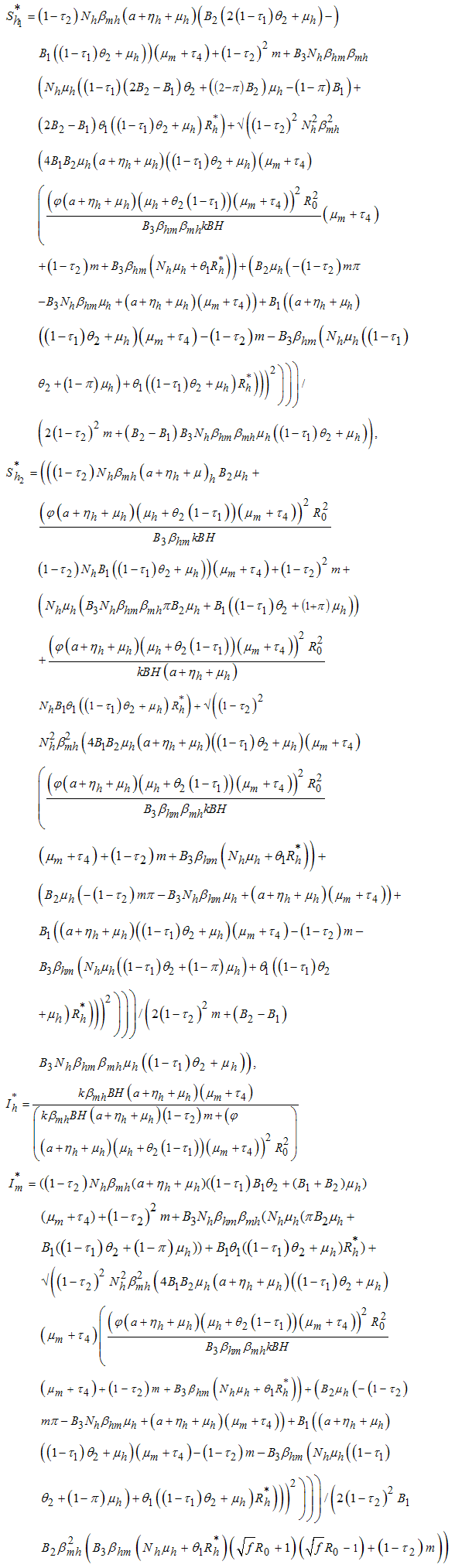 But from (3)
But from (3)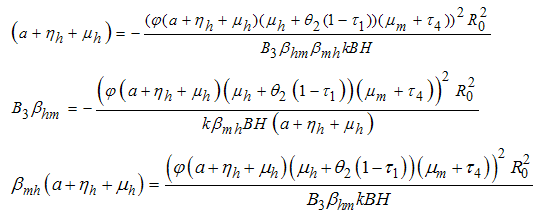 where
where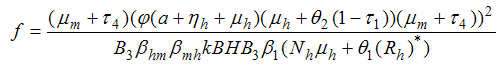
3.5.2. Local Stability of the Endemic Equilibrium
- In order to analyse the stability of the endemic equilibrium, the additive compound matrices approach is used, using the idea of [14]. Local stability of the endemic equilibrium point is determined by the variational matrix
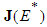 of the nonlinear system (6) corresponding to
of the nonlinear system (6) corresponding to 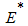 to get
to get 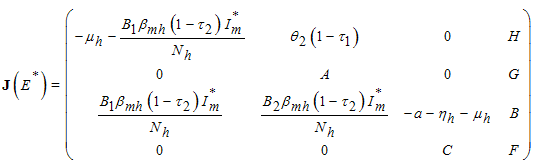 | (7) |
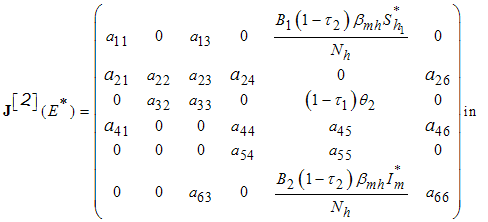 | (9) |

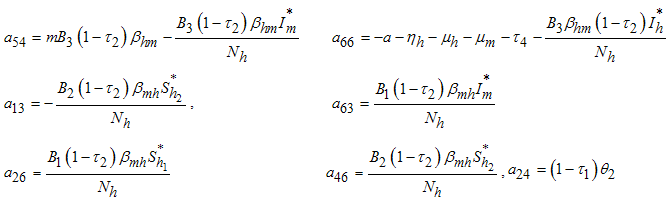 The following lemma is stated and proved by [15] to demonstrate the local stability of endemic equilibrium point
The following lemma is stated and proved by [15] to demonstrate the local stability of endemic equilibrium point 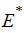 .Lemma 1: Let
.Lemma 1: Let 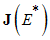 be a
be a 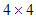 real matrix.If
real matrix.If 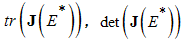 and
and 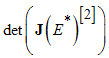 are all negative, then all eigenvalues of
are all negative, then all eigenvalues of 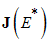 have negative real parts.Using the above Lemma, we will study the stability of the endemic equilibrium.Theorem 2: If
have negative real parts.Using the above Lemma, we will study the stability of the endemic equilibrium.Theorem 2: If 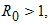 the endemic equilibrium
the endemic equilibrium 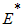 of the model (1) is locally asymptotically stable in
of the model (1) is locally asymptotically stable in 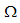 .Proof: From the Jacobian matrix
.Proof: From the Jacobian matrix 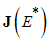 in (7), we have .
in (7), we have . 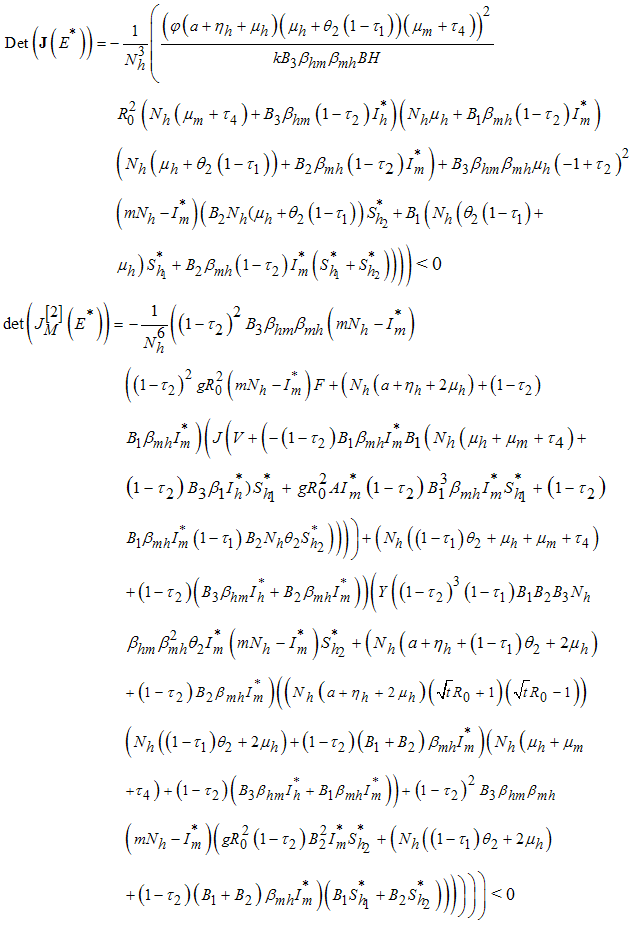 But
But 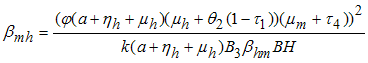 from (3)Let
from (3)Let 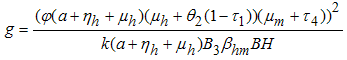 It follows that
It follows that 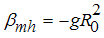 where
where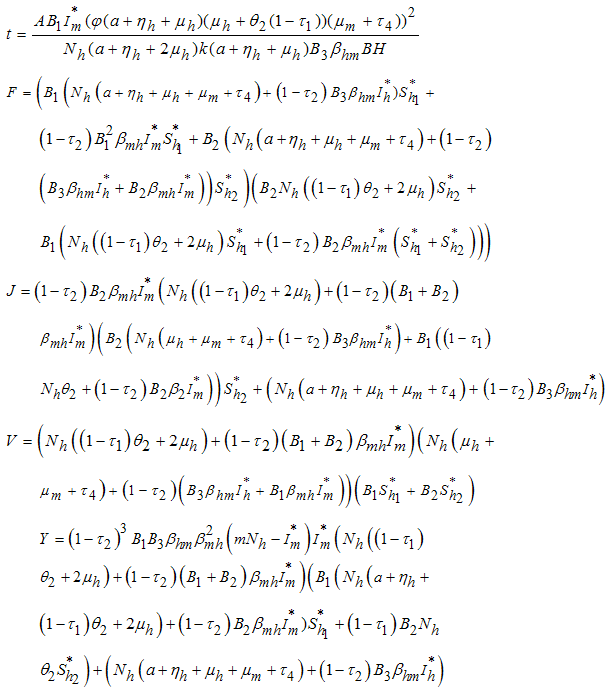 Thus, from the lemma 1, the endemic equilibrium
Thus, from the lemma 1, the endemic equilibrium 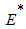 of the model system (7) is locally asymptotically stable in
of the model system (7) is locally asymptotically stable in 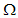 .
.3.6. Global Stability of Endemic Equilibrium Point (EEP)
- Theorem 3: If
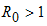 the endemic equilibrium
the endemic equilibrium 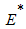 of the model system (1) is globally asymptotically stable.Proof: To establish the global stability of endemic equilibrium
of the model system (1) is globally asymptotically stable.Proof: To establish the global stability of endemic equilibrium 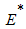 we construct the following positive Lyapunov function
we construct the following positive Lyapunov function 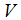 as follows;
as follows;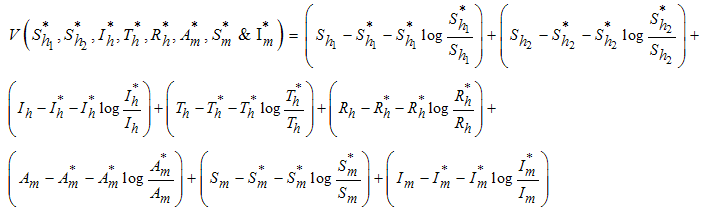 Direct calculation of the derivative of
Direct calculation of the derivative of 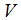 along the solutions of (1) gives,
along the solutions of (1) gives,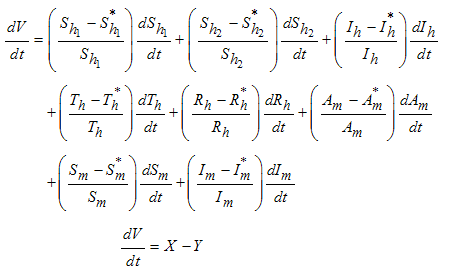 | (8) |
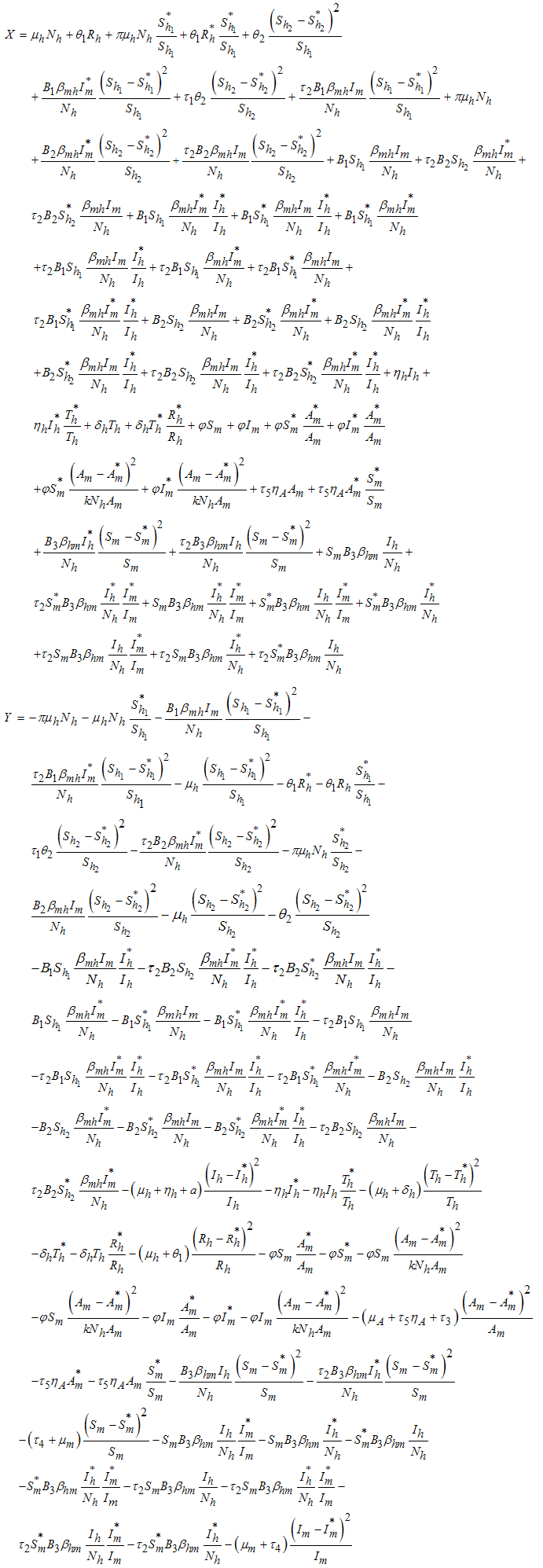 Thus from equation (8), if
Thus from equation (8), if 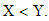 Then
Then 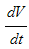 will be negative definite, implying that
will be negative definite, implying that 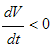 . It then follows that
. It then follows that 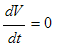 if and only if
if and only if 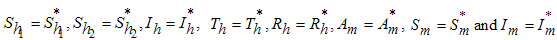 . Therefore the largest compact invariant set in
. Therefore the largest compact invariant set in 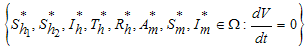 is the singleton
is the singleton 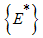 where
where 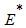 is the endemic equilibrium of the model system (1). By LaSalle’s invariant principle, then it implies that
is the endemic equilibrium of the model system (1). By LaSalle’s invariant principle, then it implies that 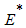 is globally asymptotically stable in
is globally asymptotically stable in 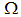 if
if 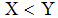 . This completes the proof.
. This completes the proof.4. Numerical Simulations
- Here, we illustrate the analytical results of the study by carrying out numerical simulations of the model system (1). Parameter values are obtained from the different literatures like (http://www.wavuti.com/2014/05/wizara-ya-afya- kitengo- cha.html), [9], [10] and [16]. Other parameter values are estimated to vary within realistic means and given as shown below.
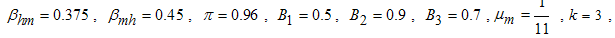
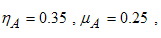
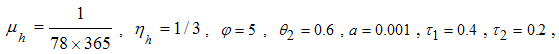
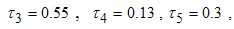
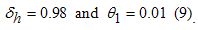 Figures 2 show the distribution of population with time in all classes of human and mosquito when no control is applied.Figures 2 show the human and mosquito populations in the absence of any control. The human infection reaches a peak between the 2th and the 20th day. The infection of the mosquitoes reaches a peak between the 10th and the 30th day. The total number of infected humans obtained from System (1) is higher than observations in Tanzania. The difference is due to the absence of the data in the whole country of Tanzania [17].
Figures 2 show the distribution of population with time in all classes of human and mosquito when no control is applied.Figures 2 show the human and mosquito populations in the absence of any control. The human infection reaches a peak between the 2th and the 20th day. The infection of the mosquitoes reaches a peak between the 10th and the 30th day. The total number of infected humans obtained from System (1) is higher than observations in Tanzania. The difference is due to the absence of the data in the whole country of Tanzania [17]. | Figure 2. Distribution of population with time in all classes of human and mosquito when no control is applied i.e. 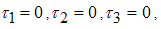 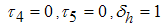 |
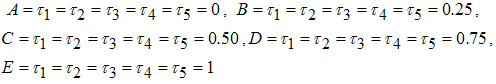
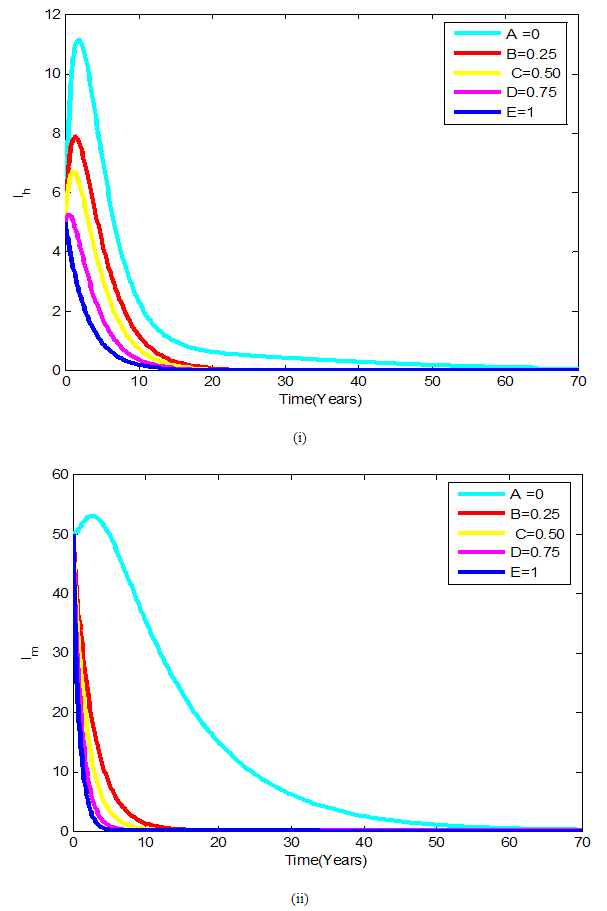 | Figure 3. (i)-(ii): Variation of infected human and mosquito populations with combine use of all five controls |
5. Formulation of the Model with Vaccination
- In this section, we develop a deterministic model that describes the dynamics of Dengue fever under application of Vaccination and treatment for humans where
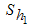 is the careful human susceptible population,
is the careful human susceptible population, 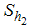 is the careless human susceptible population,
is the careless human susceptible population, 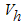 is the vaccinated human population,
is the vaccinated human population, 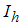 is the infected human population,
is the infected human population, 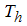 is the treated human population and
is the treated human population and 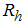 is the recovered human population,
is the recovered human population, 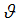 is the fraction of the vaccinated careful human susceptible,
is the fraction of the vaccinated careful human susceptible, 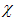 is the proportional rate at which vaccinated careful human susceptible loses effect,
is the proportional rate at which vaccinated careful human susceptible loses effect, 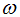 is the reaction of the vaccinated careless human susceptible,
is the reaction of the vaccinated careless human susceptible, 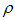 is the proportional rate at which vaccinated careless human susceptible loses effect,
is the proportional rate at which vaccinated careless human susceptible loses effect, 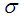 is the proportion of the vaccinated new born,
is the proportion of the vaccinated new born, 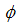 is the infection rate of vaccinated careful human susceptible and
is the infection rate of vaccinated careful human susceptible and 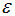 is the infection rate of vaccinated careless human susceptible. Susceptible individuals acquire Dengue fever through the bite of female Aedes mosquito with force of infections given by
is the infection rate of vaccinated careless human susceptible. Susceptible individuals acquire Dengue fever through the bite of female Aedes mosquito with force of infections given by 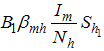 , and
, and 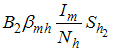 where
where 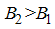 .Considering the above clarification, we then have the following schematic model flow diagram for dengue fever disease with vaccination:From the above flow diagram, the model will be governed by the following equations [17]:
.Considering the above clarification, we then have the following schematic model flow diagram for dengue fever disease with vaccination:From the above flow diagram, the model will be governed by the following equations [17]: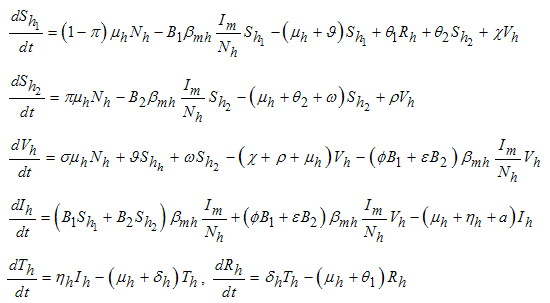 | (10) |
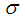 of vaccinated new born. A fraction
of vaccinated new born. A fraction 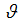 and
and 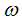 of careful and careless susceptible is vaccinated respectively. The vaccination reduces but does not eliminate susceptibility to infection. For this reason, we consider the infection rate of vaccinated people: when
of careful and careless susceptible is vaccinated respectively. The vaccination reduces but does not eliminate susceptibility to infection. For this reason, we consider the infection rate of vaccinated people: when 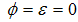 the vaccine is perfect and when
the vaccine is perfect and when 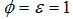 the vaccine has no effect at all. The vaccination loses effectiveness at a rate
the vaccine has no effect at all. The vaccination loses effectiveness at a rate 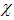 and
and 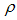 careful and careless susceptible respectively [17].
careful and careless susceptible respectively [17].5.1. Model Simulation
- Here, we perform numerical simulations of the model system (11) using the set of estimated parameter values. Parameter values are obtained from the different literatures like (http:/e/www.wavuti.com/2014/05/wizara-ya-afya-kitengo-cha.html), [9], [10], [16], other parameter values are estimated to vary within realistic means and given as
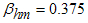 ,
, 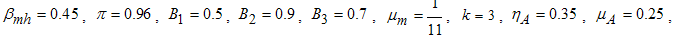
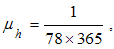
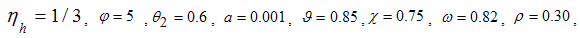
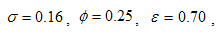
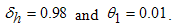 Figures 4 show the variation of infected human populations with different levels of infection rate of vaccinated careful human susceptible
Figures 4 show the variation of infected human populations with different levels of infection rate of vaccinated careful human susceptible 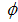 , infection rate of vaccinated careless human susceptible
, infection rate of vaccinated careless human susceptible 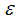 , fraction of the vaccinated careful human susceptible
, fraction of the vaccinated careful human susceptible 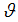 and fraction of the vaccinated careless human susceptible
and fraction of the vaccinated careless human susceptible 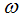 .From figure 4 we vary infection rate of vaccinated careful susceptible
.From figure 4 we vary infection rate of vaccinated careful susceptible 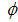 , infection rate of vaccinated careless human susceptible
, infection rate of vaccinated careless human susceptible 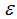 , fraction of the vaccinated careful human susceptible
, fraction of the vaccinated careful human susceptible 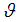 and fraction of the vaccinated careless human susceptible
and fraction of the vaccinated careless human susceptible 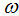 , and it is observed that the effectiveness of the vaccine reduces the disease spread.
, and it is observed that the effectiveness of the vaccine reduces the disease spread. | Figure 5. Model Flow diagram for dengue fever disease with vaccination |
6. Conclusions
- A compartmental model for Dengue fever disease was presented, The was model based on campaign of educating Careless human susceptible
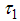 , control vector human contact
, control vector human contact 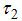 , reducing vector breeding areas
, reducing vector breeding areas 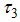 , and insecticide application
, and insecticide application 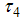 , control maturation rate from larvae to adult
, control maturation rate from larvae to adult 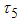 and treatment. The results show that Treatment and the controls on the transmission of dengue fever disease will have a positive effect on decreasing the growth rate of dengue fever disease. Then also shows that when
and treatment. The results show that Treatment and the controls on the transmission of dengue fever disease will have a positive effect on decreasing the growth rate of dengue fever disease. Then also shows that when 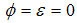 the infected human population decrease and when
the infected human population decrease and when 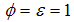 the infected human population increase.
the infected human population increase. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML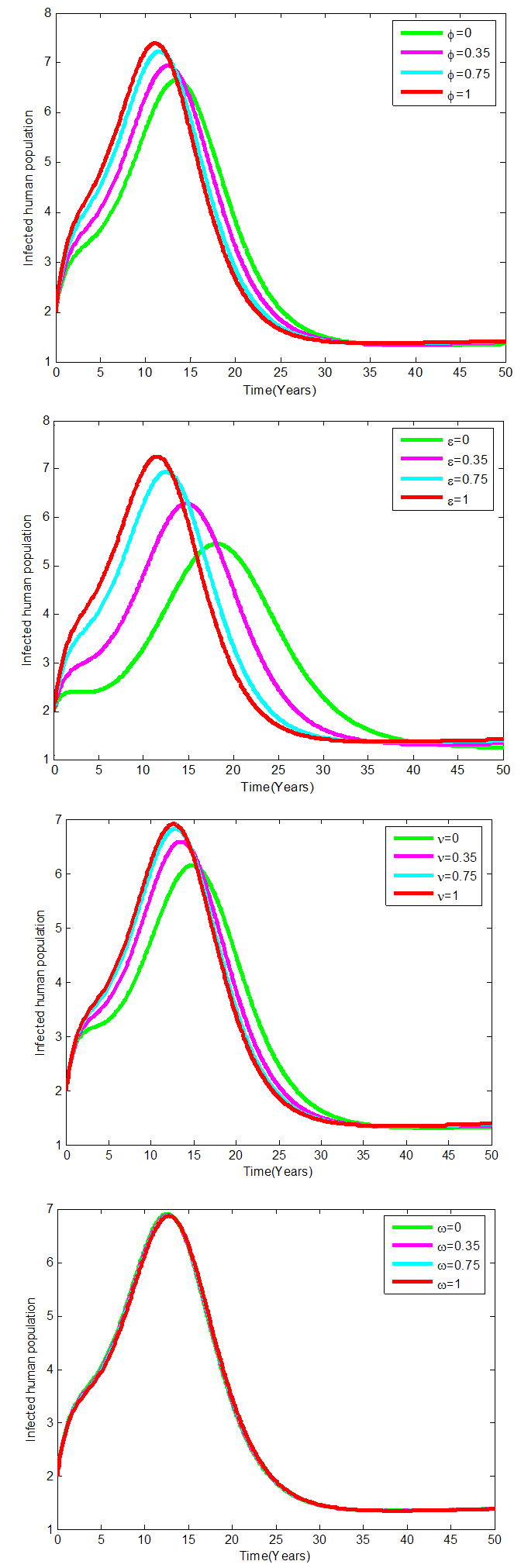
 , infection rate of vaccinated careless human susceptible
, infection rate of vaccinated careless human susceptible 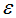 , fraction of the vaccinated careful human susceptible
, fraction of the vaccinated careful human susceptible 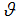 and fraction of the vaccinated careless human susceptible
and fraction of the vaccinated careless human susceptible