Neterindwa Ainea1, Estomih S. Massawe1, Oluwole Daniel Makinde2, Lucy Namkinga3
1Mathematics Department, University of Dar es Salaam, Dar es Salaam, Tanzania
2Faculty of Military Science, Stellenbosch University Private Bag X2, Saldanha, South Africa
3Department of Molecular Biology and Biotechnology, University of Dar es Salaam, Dar es Salaam, Tanzania
Correspondence to: Neterindwa Ainea, Mathematics Department, University of Dar es Salaam, Dar es Salaam, Tanzania.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper considers an optimal control analysis for HCV model by incorporating education, health care, immunization, screening of immigrants and treatment in the model. The goal is to minimize the spread of HCV disease in the community with inflow of infected immigrants and to minimize the costs of control strategies. In this context, the existence of an optimal control is proved. The results show that the effective use of optimal screening of immigrants together with education, health care, immunization and treatment has a significant impact in reducing the spread of the disease in the community.
Keywords:
Infections by Immigrants, Pontryagins maximum principle, Control Strategies, Optimal control of HCV
Cite this paper: Neterindwa Ainea, Estomih S. Massawe, Oluwole Daniel Makinde, Lucy Namkinga, Optimal Control Analysis of HCV Disease in a Community with Inflow of Infected Immigrants, American Journal of Computational and Applied Mathematics , Vol. 5 No. 1, 2015, pp. 11-17. doi: 10.5923/j.ajcam.20150501.03.
1. Introduction
Hepatitis C a most common viral infection of the liver is usually caused by hepatitis C virus. Hepatitis C virus (HCV) was first identified in the year 1989 [9]. An estimated 170 million people worldwide (3% of the world's population) are now thought to be HCV chronic carriers. It is also estimated that 85% of the individuals exposed to HCV develop chronic hepatitis C, of which about 15% have the possibility to clear the virus spontaneously within a few months of infection [9] Most common avenues through which HCV is spread are unprotected sex, sharing of contaminated needles among drug addicts and those with other STDs. Some people also get this virus from tattoo and piercing salons. It is also possible to contract HCV at birth, as it can be transmitted from mother to baby. As a matter of fact, Hepatitis C virus in pregnancy is emerging and today it is becoming an increasing source of concern [4]. Mathematical modelling of the spread of infectious diseases continues to become an important tool in understanding the dynamics of diseases and in decision making processes regarding diseases intervention programs for disease in many countries. For instance, [1] formulated and analysed a mathematical model on the effect of Treatment and Infected Immigrants on the spread of Hepatitis C Virus disease at Acute and Chronic stages. [3] investigated the dynamic behaviour of an SEI (Susceptible-Exposed- Infective) model with acute and chronic stages.Optimal control theory has found wide-ranging applications in biological and ecological problems [6]. Specifically, there have been various studies of epidemiological models where optimal control methods have been applied. [8] used optimal control theory to determine the optimal timing and intensity of an HCV antiviral treatment programme for active injecting drug users (IDUs) with a variety of policy objectives, budget constraints, and prevalence settings. [2] determined an optimal treatment strategy using interferon and ribavirin, through mathematical modelling. [9] considered a deterministic multipatch hepatitis C virus model in order to study the impact of movement between the patches and optimal control movement of infectives and treatments on the transmission dynamics of the disease. Studies conducted so far have not focused on the use of optimal control theory to minimize the cost of the control strategies (education, health care, immunization, screening of immigrants and treatment) of HCV disease. The main outputs of these findings will be minimum spread of HCV disease, costs, contribution to the design of public health policy, suggestion on future research and decision framework for programme implementation.
2. Optimal Control Analysis
The model sub-divides the total human population at time 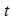 , denoted by
, denoted by 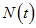 , into sub-populations of susceptible individuals
, into sub-populations of susceptible individuals 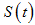 , exposed individuals (infected but not infectious)
, exposed individuals (infected but not infectious) 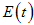 , individuals with acute infection (initially infected)
, individuals with acute infection (initially infected) 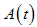 , chronic infected individuals (infectious individuals)
, chronic infected individuals (infectious individuals) 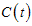 and recovered individuals
and recovered individuals 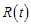 . Total population at time
. Total population at time 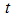 is given by
is given by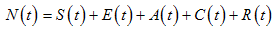 | (1) |
The interaction between the classes will be assumed as follows: exposed 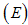 , acute infected
, acute infected 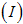 and chronic infected
and chronic infected 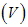 immigrants enter into the population with the rates
immigrants enter into the population with the rates 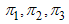 respectively. Susceptible individuals contacts with acute and chronic infected individuals at rates
respectively. Susceptible individuals contacts with acute and chronic infected individuals at rates 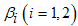 respectively. Susceptible individuals acquire HCV infection following contact with an active infectious individual at a rate
respectively. Susceptible individuals acquire HCV infection following contact with an active infectious individual at a rate 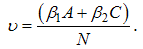 The exposed individuals develop to acute infected group at a rate
The exposed individuals develop to acute infected group at a rate 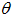 while acute infective develop to chronic group at a rate
while acute infective develop to chronic group at a rate 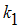 and exposed individuals move to chronic class at the rate
and exposed individuals move to chronic class at the rate 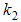 . The infectious individuals recovered at a rate
. The infectious individuals recovered at a rate 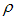 , and recovered individual loses immunity and become immediately susceptible again at a rate
, and recovered individual loses immunity and become immediately susceptible again at a rate 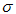 . Acute and chronic infected individuals undergo death due to the disease at the rate
. Acute and chronic infected individuals undergo death due to the disease at the rate 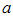 and
and 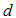 respectively.It is assumed that the rate of contact of susceptibles with chronic individuals is much less than acute infectives
respectively.It is assumed that the rate of contact of susceptibles with chronic individuals is much less than acute infectives 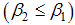 because on chronic stage people become aware of their infection and may choose to use control measures and change their behaviour and thus may contribute little in spreading the infection.Taking into account the above considerations, the model will be governed by the following system of equations:
because on chronic stage people become aware of their infection and may choose to use control measures and change their behaviour and thus may contribute little in spreading the infection.Taking into account the above considerations, the model will be governed by the following system of equations: 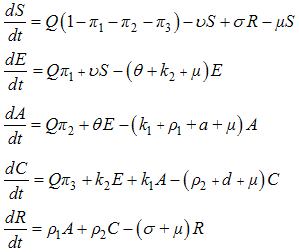 | (2) |
with nonnegative initial conditions and 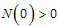 .We introduce into the model (2), time dependent preventive
.We introduce into the model (2), time dependent preventive 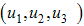 efforts as controls to minimize the spread of the disease. We wish to minimize the spread of HCV disease, as well as minimizing the cost associated with control strategies. For effective control to be achievable in a finite time, we need to consider time dependent controls. We then proceed by applying Pontryagins maximum principle to determine the conditions for effective control in finite time. We introduce into the model (2), education, health care, immunization
efforts as controls to minimize the spread of the disease. We wish to minimize the spread of HCV disease, as well as minimizing the cost associated with control strategies. For effective control to be achievable in a finite time, we need to consider time dependent controls. We then proceed by applying Pontryagins maximum principle to determine the conditions for effective control in finite time. We introduce into the model (2), education, health care, immunization 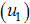 , screening of immigrants
, screening of immigrants 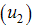 and treatment
and treatment 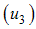 as time dependent controls to curtail the spread of HCV disease. The model (2) becomes
as time dependent controls to curtail the spread of HCV disease. The model (2) becomes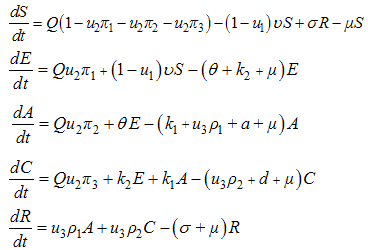 | (3) |
Here, 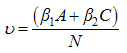 where
where 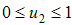 , is the screening control,
, is the screening control, 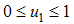 is the control on education, healthcare and immunization and
is the control on education, healthcare and immunization and 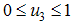 , is the treatment control for
, is the treatment control for 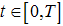 . To investigate the optimal level of efforts that would be needed to control the disease, we form the objective function, which is to minimize the spread of the disease and the cost of applying the control
. To investigate the optimal level of efforts that would be needed to control the disease, we form the objective function, which is to minimize the spread of the disease and the cost of applying the control 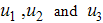 .
.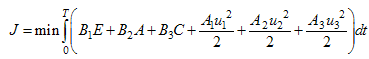 | (4) |
where 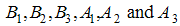 are positive weights. The terms
are positive weights. The terms 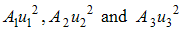 are the costs associated with
are the costs associated with 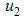 (screening of immigrants),
(screening of immigrants), 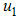 (education, health care and immunization) and
(education, health care and immunization) and 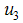 (treatment). With the given objective function
(treatment). With the given objective function 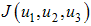 , our goal is to minimize the spread of the disease, while minimizing the cost of controls
, our goal is to minimize the spread of the disease, while minimizing the cost of controls 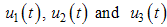 . We thus seek an optimal control triple
. We thus seek an optimal control triple 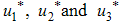 such that
such that 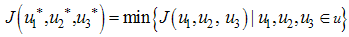 | (5) |
Here 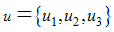 such that
such that 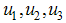 are measurable with
are measurable with 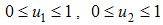 and
and 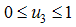 for
for 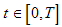 is the control set. The necessary conditions that an optimal control problem must satisfy come from Pontryagin’s maximum principle [10]. This principle converts (3)-(4) into a problem of minimizing pointwise a Hamiltonian, with respect to
is the control set. The necessary conditions that an optimal control problem must satisfy come from Pontryagin’s maximum principle [10]. This principle converts (3)-(4) into a problem of minimizing pointwise a Hamiltonian, with respect to 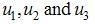
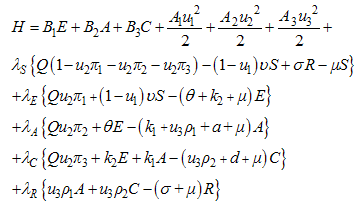 | (6) |
Where the 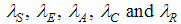 are the adjoint variables or co-state variables. By applying Pontryagin’s maximum principle [10] and the existence result for the optimal control from [3], we obtainProposition1. For optimal control triple
are the adjoint variables or co-state variables. By applying Pontryagin’s maximum principle [10] and the existence result for the optimal control from [3], we obtainProposition1. For optimal control triple 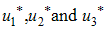 that minimizes
that minimizes 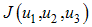 over
over 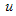 , then there exist adjoint variables
, then there exist adjoint variables 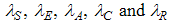 satisfying.
satisfying.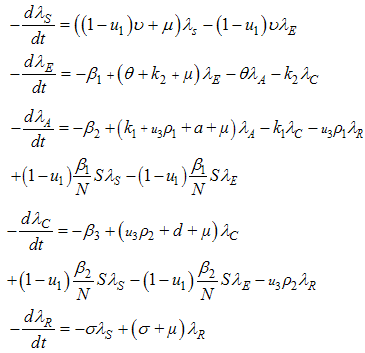 | (5) |
and with transversality conditions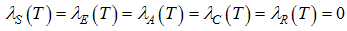 | (6) |
and by optimality conditions;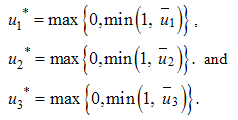 To find
To find 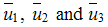 we first solve the optimality conditions given by
we first solve the optimality conditions given by 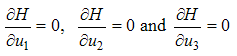 | (7) |
We differentiate equestion (6) with respect to 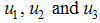 to get
to get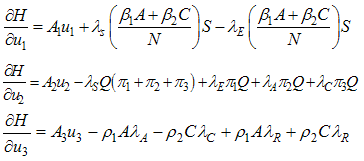 | (8) |
We therefore solve for 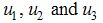 by equating
by equating 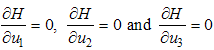 as described by Lenhart and Workman (2002).By equating system (8) to zero we obtain
as described by Lenhart and Workman (2002).By equating system (8) to zero we obtain 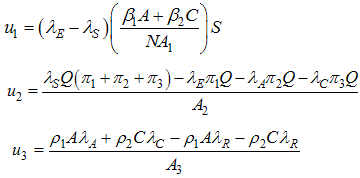 | (9) |
From the system (9) then 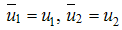
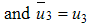 . Hence the optimality conditions is written as
. Hence the optimality conditions is written as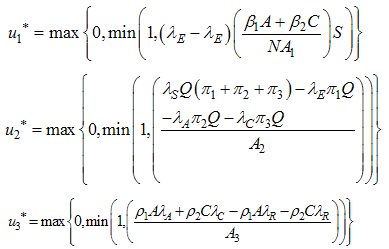 | (10) |
By standard control arguments involving the bounds on the controls, we conclude similarly as Okosun (2012) that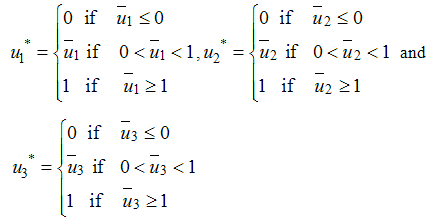 | (11) |
According to the prior boundedness of the state system, the adjoint system and the resulting Lipschitz structure of the ODEs, we obtain the uniqueness of the optimal control for small  . The uniqueness of the optimal control follows from the uniqueness of the optimality system, which consist of equations (5) and (6) and transversality condition with characterization (10).There is a restriction on the length of time interval in order to guarantee the uniqueness of the optimality system. This smallness restriction of the length on the time due to the opposite time orientations of (5) and (6); the state problem has initial values and the adjoint problem has final values. This restriction is common in control problems [see 5, 6, 7]
. The uniqueness of the optimal control follows from the uniqueness of the optimality system, which consist of equations (5) and (6) and transversality condition with characterization (10).There is a restriction on the length of time interval in order to guarantee the uniqueness of the optimality system. This smallness restriction of the length on the time due to the opposite time orientations of (5) and (6); the state problem has initial values and the adjoint problem has final values. This restriction is common in control problems [see 5, 6, 7]
3. Simulation for the Optimal Control Problem
In this section, we study numerically an optimal transmission parameter control for the HCV model. In order to study the effects of control  (screening rate) and control
(screening rate) and control  (education, health care and immunization) and
(education, health care and immunization) and 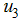 (treatment) on transmission dynamics of HCV infection, the numerical simulations of the model (3) are carried out using the following set of estimated values:
(treatment) on transmission dynamics of HCV infection, the numerical simulations of the model (3) are carried out using the following set of estimated values: 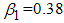 ,
, 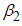
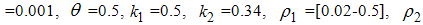
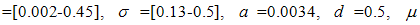
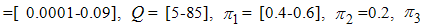
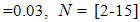 . Assume the weights at final time are being kept fixed as,
. Assume the weights at final time are being kept fixed as, 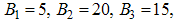
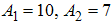 , to illustrate the effect of various optimal strategies on the transmission dynamics of HCV. Figure (1) shows the simulation of the model with control
, to illustrate the effect of various optimal strategies on the transmission dynamics of HCV. Figure (1) shows the simulation of the model with control 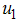 (education, health care and immunization) and screening of immigrants
(education, health care and immunization) and screening of immigrants 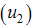 .
.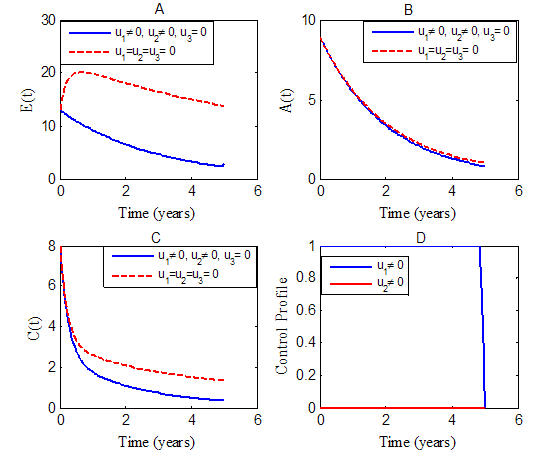 | Figure 1. Simulations of the model showing the effects of education, health care, immunization  and screening and screening 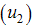 on the spread of HCV on the spread of HCV |
The screening control 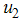 and the education, health care, immunization
and the education, health care, immunization 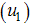 are used to optimize the objective functional
are used to optimize the objective functional  while we set the treatment
while we set the treatment 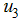 , to zero . We observed in figure 1(A) that due to the control strategies, the number of exposed population decreases while the population of exposed increases when there is no control. A similar decrease is observed in figure 1 (B) and (C) for infectious population in the presence of control strategies while an increased number is observed for the uncontrolled case. The control profile is shown in figure 1(D) we see that the optimal education, health care, immunization
, to zero . We observed in figure 1(A) that due to the control strategies, the number of exposed population decreases while the population of exposed increases when there is no control. A similar decrease is observed in figure 1 (B) and (C) for infectious population in the presence of control strategies while an increased number is observed for the uncontrolled case. The control profile is shown in figure 1(D) we see that the optimal education, health care, immunization 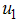 is at the upper bound, till the time
is at the upper bound, till the time 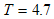 years before dropping to the lower bound while the optimal screening
years before dropping to the lower bound while the optimal screening 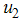 is at the lower bound till the final time. It observed that
is at the lower bound till the final time. It observed that 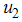 did not contribute meaningfully to the elimination of the disease except that it increases the control operational cost. Hence for cost effectiveness and disease optimal control strategy
did not contribute meaningfully to the elimination of the disease except that it increases the control operational cost. Hence for cost effectiveness and disease optimal control strategy 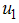 seems sufficient. These results show that in the presence of screening rate without education, health care and immunization, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population together with education, health care and immunization will be beneficial to the community for the control of HCV disease. Figure (2) shows the simulation of the model with screening
seems sufficient. These results show that in the presence of screening rate without education, health care and immunization, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population together with education, health care and immunization will be beneficial to the community for the control of HCV disease. Figure (2) shows the simulation of the model with screening 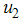 and treatment
and treatment 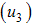
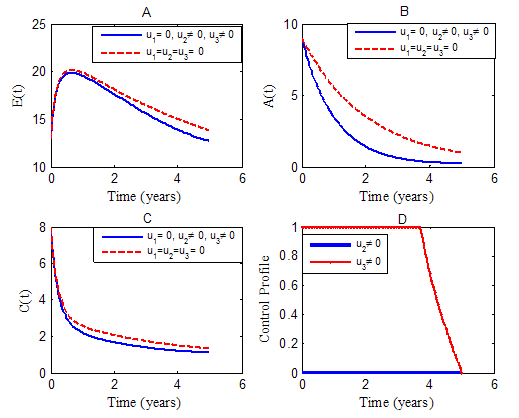 | Figure 2. Simulations of the model showing the effects of screening 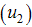 and treatment and treatment 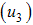 on the spread of HCV on the spread of HCV |
The use of screening control 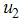 and the treatment
and the treatment 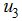 are used to optimize the objective functional
are used to optimize the objective functional 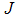 while we set, education, health care, immunization
while we set, education, health care, immunization 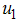 to zero. In figure (2), the results show a significant difference in the number of exposed humans
to zero. In figure (2), the results show a significant difference in the number of exposed humans  acute infected humans
acute infected humans 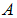 and chronic infected humans
and chronic infected humans 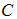 with optimal strategy compared to
with optimal strategy compared to 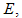
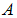 and
and 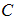 without control. Specifically, we observed in fig. 2(A) that the control strategies lead to a decrease in the number of exposed humans
without control. Specifically, we observed in fig. 2(A) that the control strategies lead to a decrease in the number of exposed humans 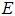 as against increases in the uncontrolled case. Similarly in figure 2(B) and (C), the uncontrolled case resulted in increased number of acute infected humans
as against increases in the uncontrolled case. Similarly in figure 2(B) and (C), the uncontrolled case resulted in increased number of acute infected humans 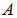 and chronic infected humans while the control strategy lead to a decrease in the number of infected humans.Figure (3) shows the simulation of the model where by controls
and chronic infected humans while the control strategy lead to a decrease in the number of infected humans.Figure (3) shows the simulation of the model where by controls 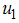 and
and 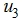 are optimized.
are optimized. | Figure 3. Simulations of the model showing the effects of education, health care, immunization 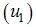 and treatment and treatment 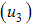 on the spread of HCV on the spread of HCV |
We optimize the objective function 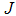 using the education, health care, immunization
using the education, health care, immunization 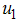 and treatment
and treatment 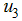 while the screening of immigrants control
while the screening of immigrants control 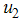 is set to zero. The results in figure 3(A-C) show a significance difference in the numbers of exposed and infectious humans with optimal strategy compared to the number without controls. Due to the control strategies, the number of exposed population decreses while the population of exposed increases when there is no control. In figure 3(B) and (C), the infectious population decrease in the presence of control strategies while an incresed number is observed for the uncontrolled case. From the control profile shown in figure 3(D), the results suggests control on education, health care, immunization
is set to zero. The results in figure 3(A-C) show a significance difference in the numbers of exposed and infectious humans with optimal strategy compared to the number without controls. Due to the control strategies, the number of exposed population decreses while the population of exposed increases when there is no control. In figure 3(B) and (C), the infectious population decrease in the presence of control strategies while an incresed number is observed for the uncontrolled case. From the control profile shown in figure 3(D), the results suggests control on education, health care, immunization 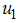 to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment
to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment 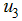 to be at the upper bound for 3.7 yrs before dropping gradually to the lower bound at final time. Figure (4) shows the simulation of the model where by both controls
to be at the upper bound for 3.7 yrs before dropping gradually to the lower bound at final time. Figure (4) shows the simulation of the model where by both controls 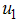 ,
, 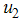 and
and 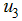 are optimized.
are optimized.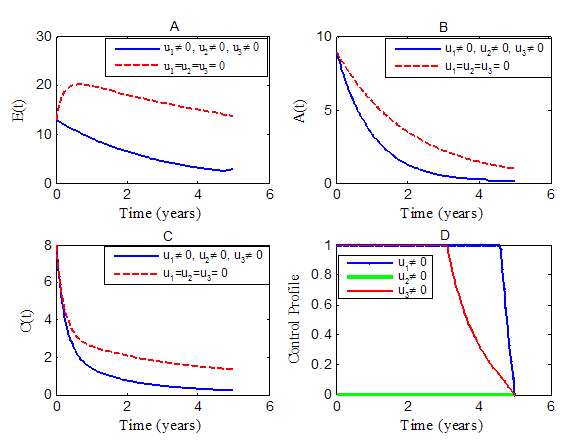 | Figure 4. Simulations of the model showing the effects of all controls on spread of HCV |
We use all the three controls, education, health care, immunization 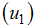 , screening of immigrants
, screening of immigrants 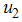 and treatment
and treatment 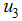 to optimize the objective functional
to optimize the objective functional 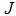 . We observed in figure 4(A-C) that the control strategies resulted in a decrease in the numbers of exposed
. We observed in figure 4(A-C) that the control strategies resulted in a decrease in the numbers of exposed 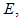 acute infected
acute infected 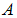 and chronic infected
and chronic infected 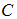 while there is increases in the numbers of
while there is increases in the numbers of 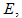
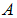 and
and 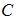 in the uncontrolled cases. The control profile in figure 4(D) suggests that education, health care, immunization
in the uncontrolled cases. The control profile in figure 4(D) suggests that education, health care, immunization 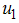 to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment
to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment 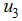 to be at the upper bound for 3.7 years before dropping gradually to the lower bound at final time. The optimal screening
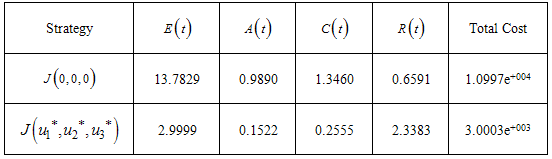
to be at the upper bound for 3.7 years before dropping gradually to the lower bound at final time. The optimal screening 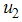 is at the lower bound till the final time. These results show that in the presence of screening rate without education, health care, immunization and treatment, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population with education, health care, immunization and treatment will be beneficial to the community for the control of HCV disease. From figures (1-4) and table 1, it is clear that the spread of the disease decreased and the total cost is also decreased by the optimal control policy.From Table (1), it is noted that when both controls are set to zero
is at the lower bound till the final time. These results show that in the presence of screening rate without education, health care, immunization and treatment, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population with education, health care, immunization and treatment will be beneficial to the community for the control of HCV disease. From figures (1-4) and table 1, it is clear that the spread of the disease decreased and the total cost is also decreased by the optimal control policy.From Table (1), it is noted that when both controls are set to zero 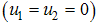 , the cost of the objective function is much (1.0997e+004) while the total cost is small (3.0003e+003) when all controls
, the cost of the objective function is much (1.0997e+004) while the total cost is small (3.0003e+003) when all controls 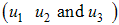 are used to optimize the objective function . It is shown that the spread of the decreses when all controls are optimized decreases at final time compared to the case without control. All controls
are used to optimize the objective function . It is shown that the spread of the decreses when all controls are optimized decreases at final time compared to the case without control. All controls 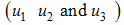 result in a significant increase in the number of recovered individuals at the final time compared to the uncontrolled case.
result in a significant increase in the number of recovered individuals at the final time compared to the uncontrolled case. Table 1. The different final states and total cost
 |
| |
|
4. Conclusions
In this paper, we performed optimal control analysis for HCV model. Using Pontryagin’s maximum principle we derived and analyzed the conditions for optimal control of the disease with effective use of education, health care, immunization, screening of immigrants and treatment. The results suggest that the effective optimal screening of immigrants together with education, health care, immunization and treatment has a significant impact in reducing the spread of the disease.
References
| [1] | Ainea, N., Massawe, E.S., and Makinde, O.D. 2012. Modelling the Effect of Treatment and Infected Immi grants on the Spread of Hepatitis C Virus Disease with Acute and Chronic Stages. American Journal of Computational and Applied Mathematics 1:10-20. |
| [2] | Chakrabarty, S.P., and Joshi H.R. 2009. Optimally con trolled treatment strategy using interferon and ribavirin for hepatitis C. Journal of Biological Systems 17(1):97-110. |
| [3] | Fleming, W.H., Rishel, R.W. 1975. Deterministic and Stochastic Optimal Control. Springer Verlag, New York. |
| [4] | Jamieson, D.J., Skunodom, N., Chaowanachan, T. 2008. Infection with hepatitis C virus among HIV infected pregnant women in Thailand. Infectious Disease in Obstetrics and Gynecology, doi: 10.1155/2008/840948. |
| [5] | Joshi, H.R. 2002. Optimal control of an HIV immu nology model. Optim. Control Appl. Math. 23, 199–213. |
| [6] | Lenhart, S., and Workman, J.T. 2007. Optimal con trol applied to biological models, Mathematical and Com putational Biology Series. Chapman and Hall/CRC. |
| [7] | Makinde, O.D., and Okosun, K.O. 2011. Impact of Chemo-therapy on Optimal Control of Malaria Disease with Infected Immigrants, BioSystems 104: 32-41. |
| [8] | Martin, N.K., Ashley, B., Pitcher, A.B., Vickerman, P., Vassal, A., and Hickman, M. 2011. Optimal control of hepatitis C antiviral treatment programme delivery for prevention amongst a population of injecting drug users. PLos One 6(8): e22309. |
| [9] | Okosun, K.O. 2014, Impact and Optimal Control of Movement on a Multipatch Hepatitis C Virus model. Pure Appl. Math.5: 80-95. |
| [10] | Pontryagin, L.S., Boltyanskii V.G., Gamkrelidze R.V. and Mishchenko E.F. 1962. The Mathematical The ory of Optimal Processes. New York. |
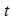 , denoted by
, denoted by 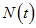 , into sub-populations of susceptible individuals
, into sub-populations of susceptible individuals 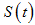 , exposed individuals (infected but not infectious)
, exposed individuals (infected but not infectious) 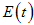 , individuals with acute infection (initially infected)
, individuals with acute infection (initially infected) 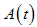 , chronic infected individuals (infectious individuals)
, chronic infected individuals (infectious individuals) 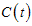 and recovered individuals
and recovered individuals 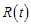 . Total population at time
. Total population at time 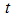 is given by
is given by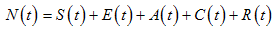
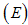 , acute infected
, acute infected 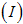 and chronic infected
and chronic infected 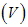 immigrants enter into the population with the rates
immigrants enter into the population with the rates 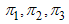 respectively. Susceptible individuals contacts with acute and chronic infected individuals at rates
respectively. Susceptible individuals contacts with acute and chronic infected individuals at rates 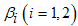 respectively. Susceptible individuals acquire HCV infection following contact with an active infectious individual at a rate
respectively. Susceptible individuals acquire HCV infection following contact with an active infectious individual at a rate 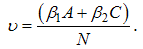 The exposed individuals develop to acute infected group at a rate
The exposed individuals develop to acute infected group at a rate 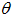 while acute infective develop to chronic group at a rate
while acute infective develop to chronic group at a rate 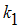 and exposed individuals move to chronic class at the rate
and exposed individuals move to chronic class at the rate 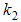 . The infectious individuals recovered at a rate
. The infectious individuals recovered at a rate 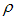 , and recovered individual loses immunity and become immediately susceptible again at a rate
, and recovered individual loses immunity and become immediately susceptible again at a rate 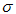 . Acute and chronic infected individuals undergo death due to the disease at the rate
. Acute and chronic infected individuals undergo death due to the disease at the rate 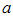 and
and 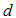 respectively.It is assumed that the rate of contact of susceptibles with chronic individuals is much less than acute infectives
respectively.It is assumed that the rate of contact of susceptibles with chronic individuals is much less than acute infectives 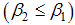 because on chronic stage people become aware of their infection and may choose to use control measures and change their behaviour and thus may contribute little in spreading the infection.Taking into account the above considerations, the model will be governed by the following system of equations:
because on chronic stage people become aware of their infection and may choose to use control measures and change their behaviour and thus may contribute little in spreading the infection.Taking into account the above considerations, the model will be governed by the following system of equations: 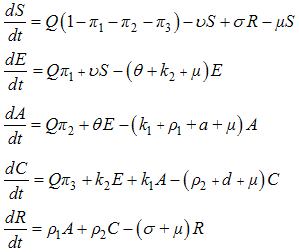
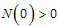 .We introduce into the model (2), time dependent preventive
.We introduce into the model (2), time dependent preventive 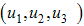 efforts as controls to minimize the spread of the disease. We wish to minimize the spread of HCV disease, as well as minimizing the cost associated with control strategies. For effective control to be achievable in a finite time, we need to consider time dependent controls. We then proceed by applying Pontryagins maximum principle to determine the conditions for effective control in finite time. We introduce into the model (2), education, health care, immunization
efforts as controls to minimize the spread of the disease. We wish to minimize the spread of HCV disease, as well as minimizing the cost associated with control strategies. For effective control to be achievable in a finite time, we need to consider time dependent controls. We then proceed by applying Pontryagins maximum principle to determine the conditions for effective control in finite time. We introduce into the model (2), education, health care, immunization 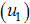 , screening of immigrants
, screening of immigrants 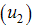 and treatment
and treatment 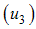 as time dependent controls to curtail the spread of HCV disease. The model (2) becomes
as time dependent controls to curtail the spread of HCV disease. The model (2) becomes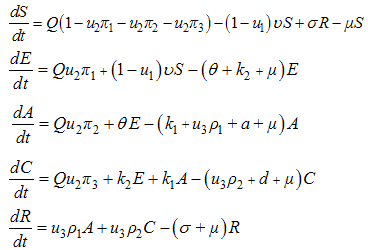
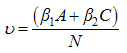 where
where 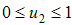 , is the screening control,
, is the screening control, 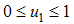 is the control on education, healthcare and immunization and
is the control on education, healthcare and immunization and 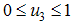 , is the treatment control for
, is the treatment control for 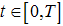 . To investigate the optimal level of efforts that would be needed to control the disease, we form the objective function, which is to minimize the spread of the disease and the cost of applying the control
. To investigate the optimal level of efforts that would be needed to control the disease, we form the objective function, which is to minimize the spread of the disease and the cost of applying the control 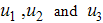 .
.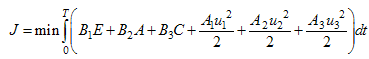
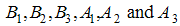 are positive weights. The terms
are positive weights. The terms 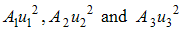 are the costs associated with
are the costs associated with 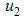 (screening of immigrants),
(screening of immigrants), 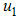 (education, health care and immunization) and
(education, health care and immunization) and 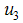 (treatment). With the given objective function
(treatment). With the given objective function 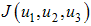 , our goal is to minimize the spread of the disease, while minimizing the cost of controls
, our goal is to minimize the spread of the disease, while minimizing the cost of controls 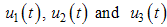 . We thus seek an optimal control triple
. We thus seek an optimal control triple 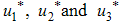 such that
such that 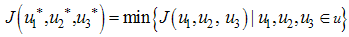
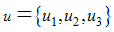 such that
such that 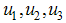 are measurable with
are measurable with 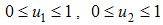 and
and 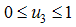 for
for 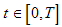 is the control set. The necessary conditions that an optimal control problem must satisfy come from Pontryagin’s maximum principle [10]. This principle converts (3)-(4) into a problem of minimizing pointwise a Hamiltonian, with respect to
is the control set. The necessary conditions that an optimal control problem must satisfy come from Pontryagin’s maximum principle [10]. This principle converts (3)-(4) into a problem of minimizing pointwise a Hamiltonian, with respect to 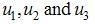
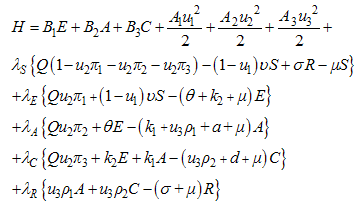
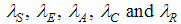 are the adjoint variables or co-state variables. By applying Pontryagin’s maximum principle [10] and the existence result for the optimal control from [3], we obtainProposition1. For optimal control triple
are the adjoint variables or co-state variables. By applying Pontryagin’s maximum principle [10] and the existence result for the optimal control from [3], we obtainProposition1. For optimal control triple 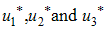 that minimizes
that minimizes 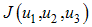 over
over 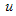 , then there exist adjoint variables
, then there exist adjoint variables 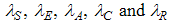 satisfying.
satisfying.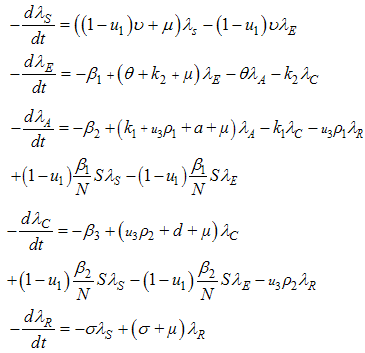
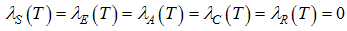
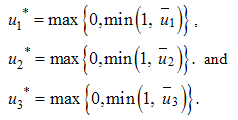 To find
To find 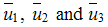 we first solve the optimality conditions given by
we first solve the optimality conditions given by 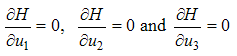
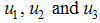 to get
to get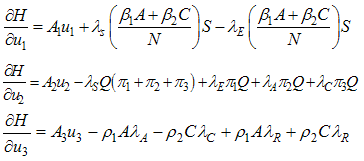
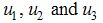 by equating
by equating 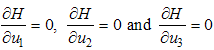 as described by Lenhart and Workman (2002).By equating system (8) to zero we obtain
as described by Lenhart and Workman (2002).By equating system (8) to zero we obtain 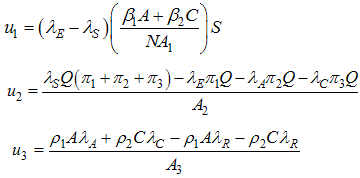
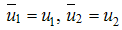
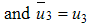 . Hence the optimality conditions is written as
. Hence the optimality conditions is written as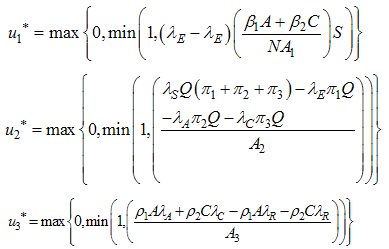
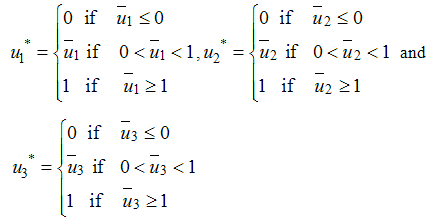
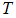 . The uniqueness of the optimal control follows from the uniqueness of the optimality system, which consist of equations (5) and (6) and transversality condition with characterization (10).There is a restriction on the length of time interval in order to guarantee the uniqueness of the optimality system. This smallness restriction of the length on the time due to the opposite time orientations of (5) and (6); the state problem has initial values and the adjoint problem has final values. This restriction is common in control problems [see 5, 6, 7]
. The uniqueness of the optimal control follows from the uniqueness of the optimality system, which consist of equations (5) and (6) and transversality condition with characterization (10).There is a restriction on the length of time interval in order to guarantee the uniqueness of the optimality system. This smallness restriction of the length on the time due to the opposite time orientations of (5) and (6); the state problem has initial values and the adjoint problem has final values. This restriction is common in control problems [see 5, 6, 7]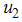 (screening rate) and control
(screening rate) and control 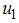 (education, health care and immunization) and
(education, health care and immunization) and 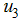 (treatment) on transmission dynamics of HCV infection, the numerical simulations of the model (3) are carried out using the following set of estimated values:
(treatment) on transmission dynamics of HCV infection, the numerical simulations of the model (3) are carried out using the following set of estimated values: 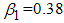 ,
, 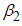
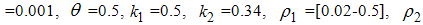
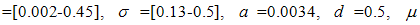
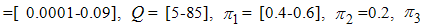
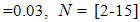 . Assume the weights at final time are being kept fixed as,
. Assume the weights at final time are being kept fixed as, 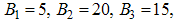
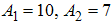 , to illustrate the effect of various optimal strategies on the transmission dynamics of HCV. Figure (1) shows the simulation of the model with control
, to illustrate the effect of various optimal strategies on the transmission dynamics of HCV. Figure (1) shows the simulation of the model with control 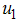 (education, health care and immunization) and screening of immigrants
(education, health care and immunization) and screening of immigrants 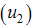 .
.
 and screening
and screening 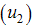 on the spread of HCV
on the spread of HCV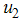 and the education, health care, immunization
and the education, health care, immunization 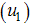 are used to optimize the objective functional
are used to optimize the objective functional 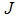 while we set the treatment
while we set the treatment 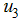 , to zero . We observed in figure 1(A) that due to the control strategies, the number of exposed population decreases while the population of exposed increases when there is no control. A similar decrease is observed in figure 1 (B) and (C) for infectious population in the presence of control strategies while an increased number is observed for the uncontrolled case. The control profile is shown in figure 1(D) we see that the optimal education, health care, immunization
, to zero . We observed in figure 1(A) that due to the control strategies, the number of exposed population decreases while the population of exposed increases when there is no control. A similar decrease is observed in figure 1 (B) and (C) for infectious population in the presence of control strategies while an increased number is observed for the uncontrolled case. The control profile is shown in figure 1(D) we see that the optimal education, health care, immunization 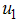 is at the upper bound, till the time
is at the upper bound, till the time 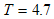 years before dropping to the lower bound while the optimal screening
years before dropping to the lower bound while the optimal screening 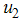 is at the lower bound till the final time. It observed that
is at the lower bound till the final time. It observed that 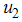 did not contribute meaningfully to the elimination of the disease except that it increases the control operational cost. Hence for cost effectiveness and disease optimal control strategy
did not contribute meaningfully to the elimination of the disease except that it increases the control operational cost. Hence for cost effectiveness and disease optimal control strategy 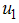 seems sufficient. These results show that in the presence of screening rate without education, health care and immunization, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population together with education, health care and immunization will be beneficial to the community for the control of HCV disease. Figure (2) shows the simulation of the model with screening
seems sufficient. These results show that in the presence of screening rate without education, health care and immunization, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population together with education, health care and immunization will be beneficial to the community for the control of HCV disease. Figure (2) shows the simulation of the model with screening 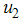 and treatment
and treatment 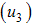

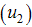 and treatment
and treatment 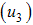 on the spread of HCV
on the spread of HCV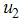 and the treatment
and the treatment 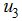 are used to optimize the objective functional
are used to optimize the objective functional 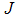 while we set, education, health care, immunization
while we set, education, health care, immunization 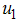 to zero. In figure (2), the results show a significant difference in the number of exposed humans
to zero. In figure (2), the results show a significant difference in the number of exposed humans 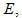 acute infected humans
acute infected humans 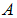 and chronic infected humans
and chronic infected humans 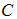 with optimal strategy compared to
with optimal strategy compared to 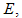
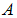 and
and 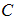 without control. Specifically, we observed in fig. 2(A) that the control strategies lead to a decrease in the number of exposed humans
without control. Specifically, we observed in fig. 2(A) that the control strategies lead to a decrease in the number of exposed humans 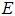 as against increases in the uncontrolled case. Similarly in figure 2(B) and (C), the uncontrolled case resulted in increased number of acute infected humans
as against increases in the uncontrolled case. Similarly in figure 2(B) and (C), the uncontrolled case resulted in increased number of acute infected humans 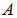 and chronic infected humans while the control strategy lead to a decrease in the number of infected humans.Figure (3) shows the simulation of the model where by controls
and chronic infected humans while the control strategy lead to a decrease in the number of infected humans.Figure (3) shows the simulation of the model where by controls 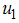 and
and 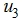 are optimized.
are optimized.
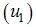 and treatment
and treatment 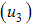 on the spread of HCV
on the spread of HCV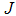 using the education, health care, immunization
using the education, health care, immunization 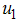 and treatment
and treatment 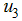 while the screening of immigrants control
while the screening of immigrants control 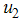 is set to zero. The results in figure 3(A-C) show a significance difference in the numbers of exposed and infectious humans with optimal strategy compared to the number without controls. Due to the control strategies, the number of exposed population decreses while the population of exposed increases when there is no control. In figure 3(B) and (C), the infectious population decrease in the presence of control strategies while an incresed number is observed for the uncontrolled case. From the control profile shown in figure 3(D), the results suggests control on education, health care, immunization
is set to zero. The results in figure 3(A-C) show a significance difference in the numbers of exposed and infectious humans with optimal strategy compared to the number without controls. Due to the control strategies, the number of exposed population decreses while the population of exposed increases when there is no control. In figure 3(B) and (C), the infectious population decrease in the presence of control strategies while an incresed number is observed for the uncontrolled case. From the control profile shown in figure 3(D), the results suggests control on education, health care, immunization 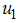 to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment
to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment 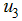 to be at the upper bound for 3.7 yrs before dropping gradually to the lower bound at final time. Figure (4) shows the simulation of the model where by both controls
to be at the upper bound for 3.7 yrs before dropping gradually to the lower bound at final time. Figure (4) shows the simulation of the model where by both controls 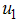 ,
, 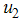 and
and 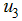 are optimized.
are optimized.
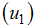 , screening of immigrants
, screening of immigrants 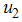 and treatment
and treatment 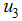 to optimize the objective functional
to optimize the objective functional 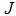 . We observed in figure 4(A-C) that the control strategies resulted in a decrease in the numbers of exposed
. We observed in figure 4(A-C) that the control strategies resulted in a decrease in the numbers of exposed 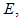 acute infected
acute infected 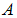 and chronic infected
and chronic infected 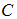 while there is increases in the numbers of
while there is increases in the numbers of 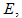
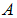 and
and 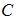 in the uncontrolled cases. The control profile in figure 4(D) suggests that education, health care, immunization
in the uncontrolled cases. The control profile in figure 4(D) suggests that education, health care, immunization 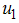 to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment
to be at the upper bound for 4.5 years before dropping gradually to the lower bound while the control on treatment 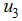 to be at the upper bound for 3.7 years before dropping gradually to the lower bound at final time. The optimal screening
to be at the upper bound for 3.7 years before dropping gradually to the lower bound at final time. The optimal screening 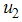 is at the lower bound till the final time. These results show that in the presence of screening rate without education, health care, immunization and treatment, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population with education, health care, immunization and treatment will be beneficial to the community for the control of HCV disease. From figures (1-4) and table 1, it is clear that the spread of the disease decreased and the total cost is also decreased by the optimal control policy.From Table (1), it is noted that when both controls are set to zero
is at the lower bound till the final time. These results show that in the presence of screening rate without education, health care, immunization and treatment, the community is not disease free and a stable endemic situation exists. Therefore, an effective and optimal screening in the population with education, health care, immunization and treatment will be beneficial to the community for the control of HCV disease. From figures (1-4) and table 1, it is clear that the spread of the disease decreased and the total cost is also decreased by the optimal control policy.From Table (1), it is noted that when both controls are set to zero 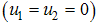 , the cost of the objective function is much (1.0997e+004) while the total cost is small (3.0003e+003) when all controls
, the cost of the objective function is much (1.0997e+004) while the total cost is small (3.0003e+003) when all controls 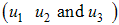 are used to optimize the objective function . It is shown that the spread of the decreses when all controls are optimized decreases at final time compared to the case without control. All controls
are used to optimize the objective function . It is shown that the spread of the decreses when all controls are optimized decreases at final time compared to the case without control. All controls 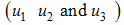 result in a significant increase in the number of recovered individuals at the final time compared to the uncontrolled case.
result in a significant increase in the number of recovered individuals at the final time compared to the uncontrolled case.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML