Ranjit R. Dhunde1, G. L. Waghmare2
1Department of Mathematics, Datta Meghe Institute of Engineering Technology & Research, Wardha (MH-India)
2Department of Mathematics, Government Science College, Gadchiroli (MH-India)
Correspondence to: Ranjit R. Dhunde, Department of Mathematics, Datta Meghe Institute of Engineering Technology & Research, Wardha (MH-India).
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we apply the double Laplace transform for solving linear partial integro-differential equations (PIDE) with a convolution kernel. Double Laplace transform converts the PIDE to an algebraic equation which can be easily solved is illustrated by solving various examples.
Keywords:
Double Laplace transform, Inverse Laplace transform, Partial integro-differential equation, Partial derivatives
Cite this paper: Ranjit R. Dhunde, G. L. Waghmare, Solving Partial Integro-Differential Equations Using Double Laplace Transform Method, American Journal of Computational and Applied Mathematics , Vol. 5 No. 1, 2015, pp. 7-10. doi: 10.5923/j.ajcam.20150501.02.
1. Introduction
We find in the literature, partial integro-differential equations are used in modelling various phenomena in science, engineering & social sciences. Jyoti Thorwe & Sachin Bhalekar [5] in 2012, used single Laplace transform method to solve linear partial integro-differential equations (PIDE) with a convolution kernel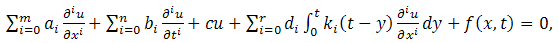 | (1.1) |
(with prescribed conditions)where 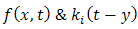 are known functions.
are known functions.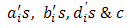 are constants or the functions of x.They converted the PIDE to an ordinary differential equation (ODE) using a Laplace transform. Solving this ODE & applying inverse Laplace transform they obtained the exact solution of the problem.The double Laplace transform [4] of a function
are constants or the functions of x.They converted the PIDE to an ordinary differential equation (ODE) using a Laplace transform. Solving this ODE & applying inverse Laplace transform they obtained the exact solution of the problem.The double Laplace transform [4] of a function 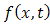 defined in the positive quadrant of the xt-plane is defined by the equation
defined in the positive quadrant of the xt-plane is defined by the equation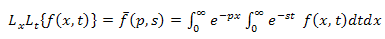 | (1.2) |
whenever that integral exist. Here p, s are complex numbers.Further the double Laplace transform [1] of first & second partial derivatives are given by 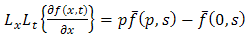 | (1.3) |
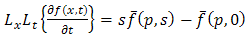 | (1.4) |
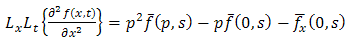 | (1.5) |
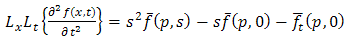 | (1.6) |
Double Laplace transform was used by Anwar et al. [2] to solve partial differential equations with Caputo fractional derivatives & fractional heat equation subject to certain initial & boundary conditions. Tarig M. Elazaki [8] in 2012, applied the modified variational iteration method & double Laplace transform to solve nonlinear convolution partial differential equations. Recently in 2013, Eltayeb & Kilicman [3] have applied the double Laplace transform to solve general linear telegraph & partial integro-differential equations. Saeed Kazem [7] implemented single Laplace transform to obtain an exact solution of some linear fractional differential equations. Jafar Saberi-Nadjafi [6] proposed some new result in n-dimensional Laplace transforms involved with Fourier cosine transform; these results provide few algorithms for evaluating some n-dimensional Laplace transform pairs.By using double Laplace transform method, we directly convert PIDE (1.1) into an algebraic equation instead of converting to ODE. Solving this algebraic equation & applying double inverse Laplace transform we obtain the exact solution. This method is illustrated by giving examples of various types already described in [5]. Convolution Theorem:If single Laplace transform of 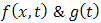 with respect to t are given by
with respect to t are given by 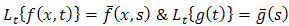 then
then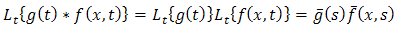 where,
where, 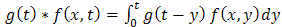 .Therefore, by using double Laplace transform convolution theorem becomes
.Therefore, by using double Laplace transform convolution theorem becomes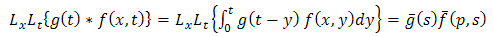 | (1.7) |
2. Solving PIDEs Using Double Laplace Transform Method
Consider PIDE (1.1),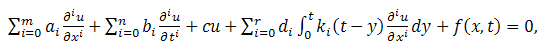 | (2.1) |
(with prescribed conditions)where 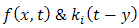 are known functions &
are known functions & 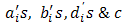 are constants.Taking double Laplace transform of PIDE (2.1), we get
are constants.Taking double Laplace transform of PIDE (2.1), we get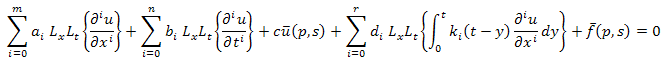 Using double Laplace transform of partial derivative & convolution theorem, we get
Using double Laplace transform of partial derivative & convolution theorem, we get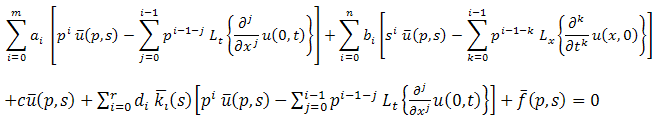 | (2.2) |
where 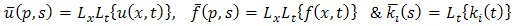 Equation (2.2) is an algebraic equation in
Equation (2.2) is an algebraic equation in 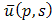 . Solving this algebraic equation & taking inverse double Laplace transform of
. Solving this algebraic equation & taking inverse double Laplace transform of 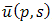 , we get an exact solution
, we get an exact solution 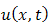 of (2.1).
of (2.1).
3. Illustrative Examples
Example 3.1: Consider the PIDE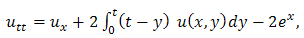 | (3.1) |
with initial condition 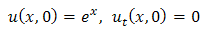 | (3.2) |
& boundary condition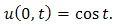 | (3.3) |
Taking double Laplace transform of equation (3.1),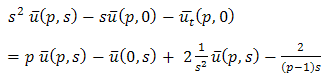 | (3.4) |
And single Laplace transforms of initial conditions (3.2) & boundary condition (3.3) are given by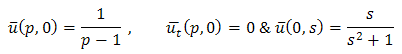 Then equation (3.4) becomes,
Then equation (3.4) becomes,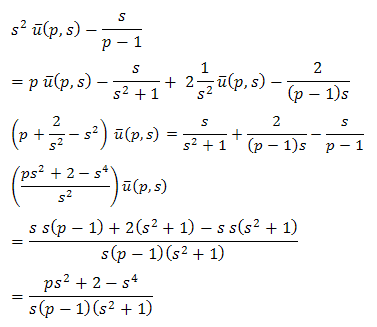
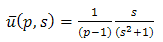 | (3.5) |
Applying inverse double Laplace transform of equation (3.5), we get 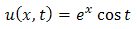 | (3.6) |
This is the required exact solution of equation (3.1).Example 3.2: Consider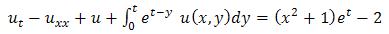 | (3.7) |
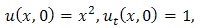 | (3.8) |
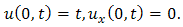 | (3.9) |
Taking double Laplace transform of equation (3.7)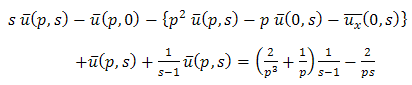 | (3.10) |
And single Laplace transforms of equation (3.8) & (3.9), we get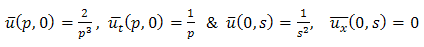 Then equation (3.10) becomes
Then equation (3.10) becomes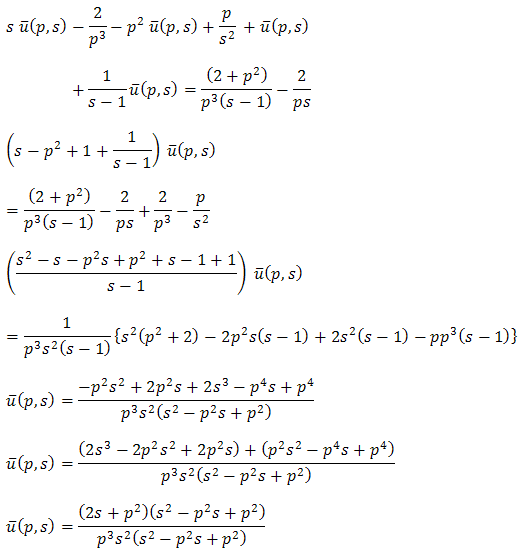
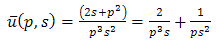 | (3.11) |
Applying inverse double Laplace transform of equation (3.11), we get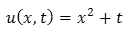 | (3.12) |
This is the required exact solution of equation (3.7).Example 3.3: Consider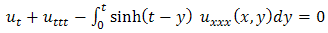 | (3.13) |
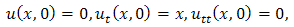 | (3.14) |
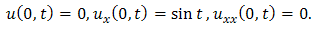 | (3.15) |
Taking double Laplace transform of equation (3.13)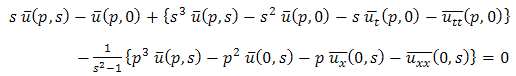 | (3.16) |
And single Laplace transforms of equation (3.14) & (3.15), we get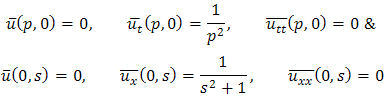 Then equation (3.16) becomes
Then equation (3.16) becomes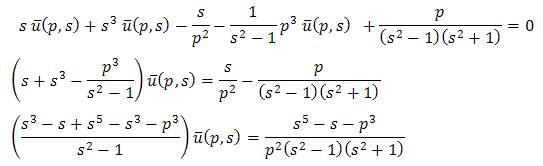
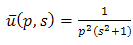 | (3.17) |
Applying inverse double Laplace transform of equation (3.17), we get 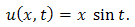 | (3.18) |
This is the required exact solution of equation (3.13).Example 3.4: Consider the PIDE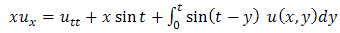 | (3.19) |
with initial condition 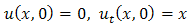 | (3.20) |
& boundary condition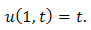 | (3.21) |
Taking double Laplace transform of equation (3.19)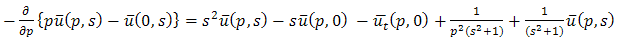 | (3.22) |
And single Laplace transforms of equation (3.20), we get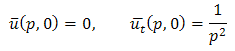 Then equation (3.22) becomes
Then equation (3.22) becomes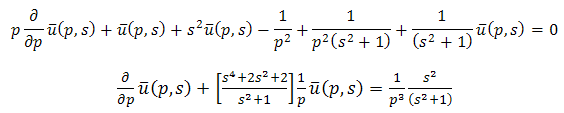 | (3.23) |
This is first order linear differential equation in  .Therefore solution of (3.23) is
.Therefore solution of (3.23) is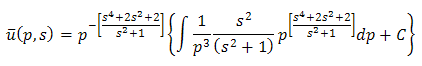 where C is a constant to be determined.
where C is a constant to be determined.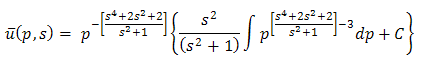
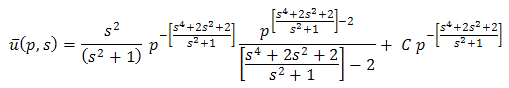
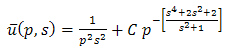 | (3.24) |
From the boundary condition (3.21),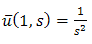 | (3.25) |
Using (3.24) & (3.25), we get 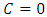
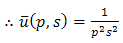 | (3.26) |
Applying inverse double Laplace transform of equation (3.26), we get 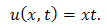 | (3.27) |
This is the required exact solution of equation (3.19).
References
| [1] | A. Estrin & T. J. Higgins, The Solution of Boundary Value Problems by Multiple Laplace Transformation, Journal of the Franklin Institute, 252 (2) (1951), pp.153 – 167. |
| [2] | A. M. O. Anwar. F. Jarad, D. Baleanu & F. Ayaz, Fractional Caputo Heat Equation within the Double Laplace Transform, Rom. Journ. Phys., Vol. 58, Nos. 1-2, pp. 15-22, Bucharest, 2013. |
| [3] | H. Eltayeb & A. Kilicman, A Note on Double Laplace Transform and Telegraphic Equations, Abstract & Applied Analysis, Volume 2013, http://dx.doi.org/10.1155/2013/932578. |
| [4] | Ian N. Sneddon, The Use of Integral Transforms, Tata Mcgraw Hill Edition 1974. |
| [5] | Jyoti Thorwe & Sachin Bhalekar, Solving Partial Integro-Differential Equations Using Laplace Transform Method, American Journal of Computational & Applied Mathematics, 2012, 2(3), pp.101-104. |
| [6] | Jafar Saberi-Nadjafi, A Computational Method for n-Dimensional Laplace Transforms Involved with Fourier Cosine Transorm, ISRN Applied Mathematics, Volume 2013, http://dx.doi.org/10.1155/2013/748417. |
| [7] | Saeed Kazem, Exact Solution of Some Linear Fractional Differential Equations by Laplace Transform, International Journal of Nonlinear Science, Vol. 16 (2013) No. 1, pp. 3-11. |
| [8] | Tarig M. Elazaki, Double Laplace Variational Iteration Method for Solution of Nonlinear Convolution Partial Differential Equations, Archives Des Sciences, Vol. 65, No. 12, Dec. 2012. |
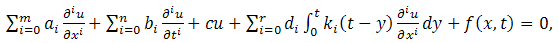
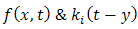 are known functions.
are known functions.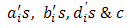 are constants or the functions of x.They converted the PIDE to an ordinary differential equation (ODE) using a Laplace transform. Solving this ODE & applying inverse Laplace transform they obtained the exact solution of the problem.The double Laplace transform [4] of a function
are constants or the functions of x.They converted the PIDE to an ordinary differential equation (ODE) using a Laplace transform. Solving this ODE & applying inverse Laplace transform they obtained the exact solution of the problem.The double Laplace transform [4] of a function 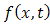 defined in the positive quadrant of the xt-plane is defined by the equation
defined in the positive quadrant of the xt-plane is defined by the equation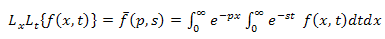
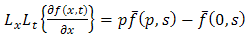
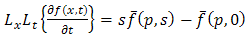
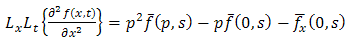
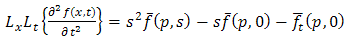
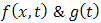 with respect to t are given by
with respect to t are given by 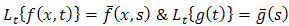 then
then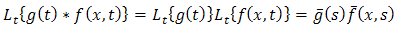 where,
where, 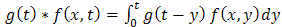 .Therefore, by using double Laplace transform convolution theorem becomes
.Therefore, by using double Laplace transform convolution theorem becomes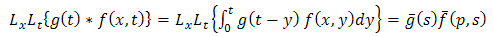
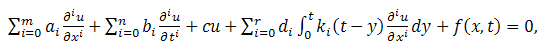
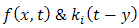 are known functions &
are known functions & 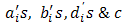 are constants.Taking double Laplace transform of PIDE (2.1), we get
are constants.Taking double Laplace transform of PIDE (2.1), we get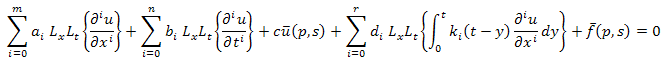 Using double Laplace transform of partial derivative & convolution theorem, we get
Using double Laplace transform of partial derivative & convolution theorem, we get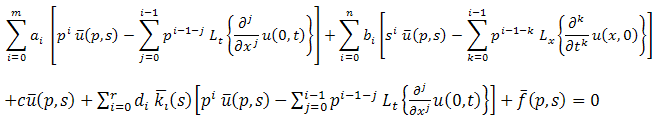
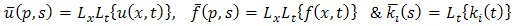 Equation (2.2) is an algebraic equation in
Equation (2.2) is an algebraic equation in 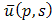 . Solving this algebraic equation & taking inverse double Laplace transform of
. Solving this algebraic equation & taking inverse double Laplace transform of 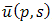 , we get an exact solution
, we get an exact solution 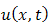 of (2.1).
of (2.1).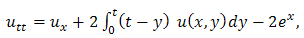
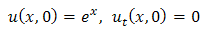
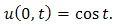
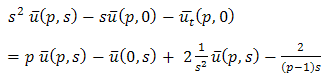
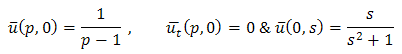 Then equation (3.4) becomes,
Then equation (3.4) becomes,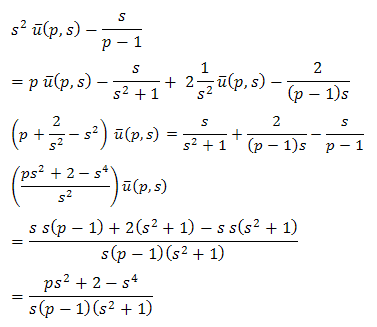
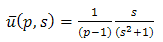
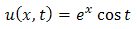
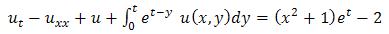
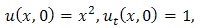
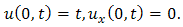
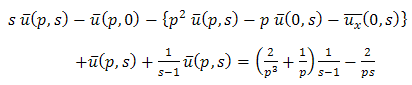
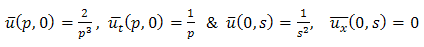 Then equation (3.10) becomes
Then equation (3.10) becomes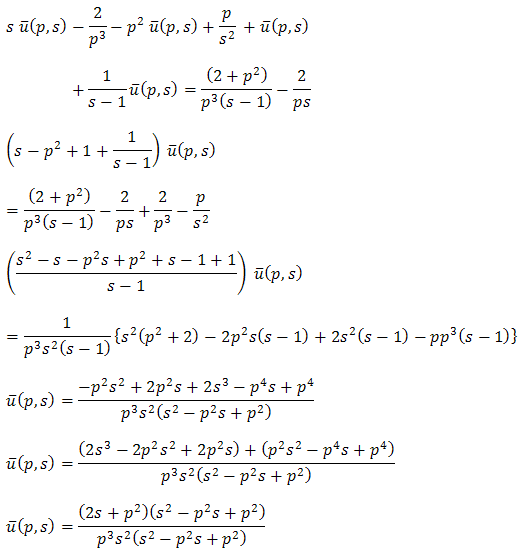
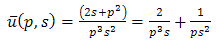
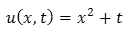
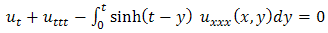
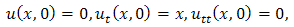
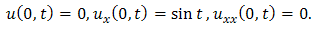
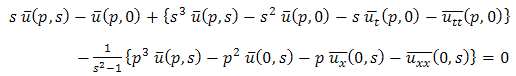
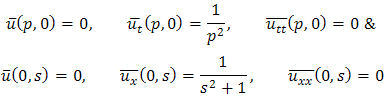 Then equation (3.16) becomes
Then equation (3.16) becomes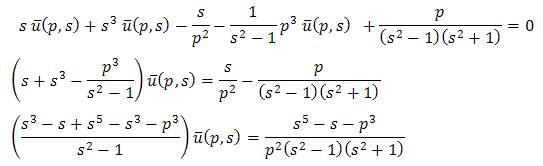
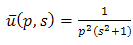
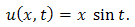
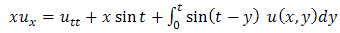
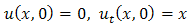
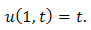
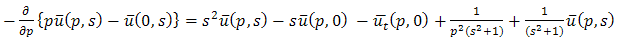
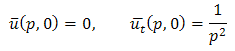 Then equation (3.22) becomes
Then equation (3.22) becomes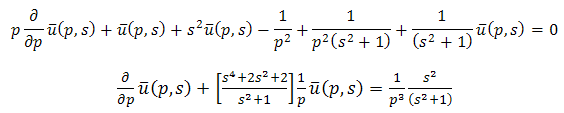
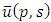 .Therefore solution of (3.23) is
.Therefore solution of (3.23) is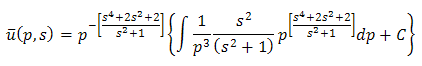 where C is a constant to be determined.
where C is a constant to be determined.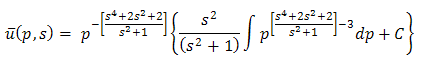
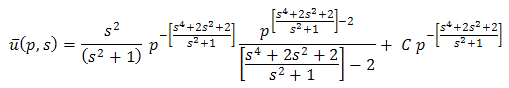
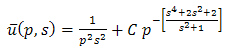
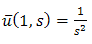
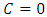
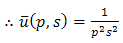
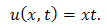
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML