-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2014; 4(6): 192-194
doi:10.5923/j.ajcam.20140406.02
A Short Note on Solving a Class of Nonlinear Ordinary Differential Equations in Applied Physics
1Islamic Azad University, Nour Branch, Dept of Mathematics
2Schiller University, Fakultät für Mathematics and Informatic
Correspondence to: M. Saravi, Islamic Azad University, Nour Branch, Dept of Mathematics.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
In this paper we apply two procedures to find out a particular solution to a class of second-order singular nonlinear ordinary differential equations (ODEs). All illustrative examples from the available literature in applied physics show that the solutions deduced by proposed procedures are particular solutions. Overall, a successful produce of particular solutions by the proposed process itself justify the effectiveness and efficiency of the procedures.
Keywords: Nonlinear ODEs, Particular solution, Ivey’s equation, Thomas-Fermi’s equation, Poisson-Boltzman’s equation
Cite this paper: M. Saravi, M. Hermann, A Short Note on Solving a Class of Nonlinear Ordinary Differential Equations in Applied Physics, American Journal of Computational and Applied Mathematics , Vol. 4 No. 6, 2014, pp. 192-194. doi: 10.5923/j.ajcam.20140406.02.
1. Introduction
- Nonlinear ordinary differential equations (ODEs) have been widely used in many areas of physics and engineering and are of significant importance in mechanical and structural dynamics for the comprehensive understanding and accurate prediction of motion and deformation. The study of nonlinear ODEs is of interest to many researchers and various methods of solution have been proposed. Surveys of the literature with numerous references, and useful bibliographies, have been given by Nayfeh [1], Sachdev [2], Jordan and Smith [3] and more recently by He [4].The solution of nonlinear ODEs due to limitation of existing particular solutions, which play an important role in property understanding the qualitative features of many phenomena, have been one of the most time-consuming and difficult affairs among researchers of nonlinear problems. Due to such difficulties, difficult tasks appear among the researchers for nonlinear problems.Most of the time a desire nonlinear transformations may be useful to solve a nonlinear ODE, but it may not be sufficient. In next section, beside of using a group of transformations, we use two simple procedures to get an exact solution for some equations that are important to be solved in applied physics.
2. Procedures with Applications
- It will be shown that a remarkably large number of ODEs with specific physical applications is included in the following class of equations [5]:
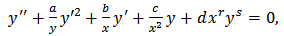 | (1) |
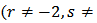
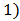 .One variant of this equation obtained by setting
.One variant of this equation obtained by setting 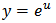 which transforms (1) to
which transforms (1) to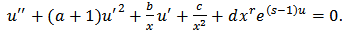 | (2) |
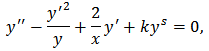 Occurring in space-charge theory, is a special case of (1) with
Occurring in space-charge theory, is a special case of (1) with 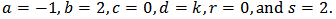 ii)- Thomas-Fermi’s equation
ii)- Thomas-Fermi’s equation 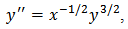
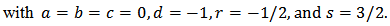 iii)- Emden-Lane-Fowler’s equation
iii)- Emden-Lane-Fowler’s equation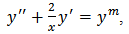 is a special case of (1) with
is a special case of (1) with 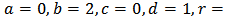
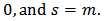 iv)- Poisson-Boltzman’s equation
iv)- Poisson-Boltzman’s equation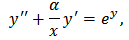 where
where 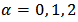 for plane, cylindrical, and spherical symmetry, respectively.This is a special case of (2) with
for plane, cylindrical, and spherical symmetry, respectively.This is a special case of (2) with 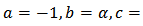
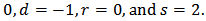 v)- Bratu’s equation
v)- Bratu’s equation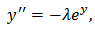 This is a special case of (2) with
This is a special case of (2) with 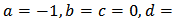
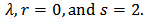 A reliable procedure for obtaining the solution may be done by using a special ansatz given by
A reliable procedure for obtaining the solution may be done by using a special ansatz given by 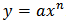 . This idea comes from this fact that these kind of equations may be solved by choosing
. This idea comes from this fact that these kind of equations may be solved by choosing 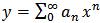 . For first three equations if we set
. For first three equations if we set 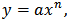 then
then 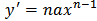 and
and 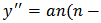
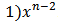 . Substituting in given equations and equating both sides, gives the values of a and n. Let us consider Ivey’s equation
. Substituting in given equations and equating both sides, gives the values of a and n. Let us consider Ivey’s equation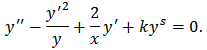 Set
Set 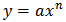 and substitute
and substitute 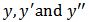 into equation. We obtain
into equation. We obtain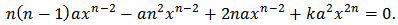 That is,
That is,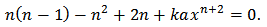 One may easily find that,
One may easily find that, 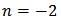 and
and 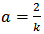 . Thus
. Thus 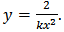 For last two equations, first by assuming
For last two equations, first by assuming 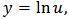 we transform equation in form of Eq. (2) then set
we transform equation in form of Eq. (2) then set 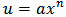 and the rest is the same as previous one. Let us consider Poisson-Boltzman’s equation with
and the rest is the same as previous one. Let us consider Poisson-Boltzman’s equation with 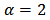
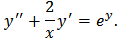 If we set
If we set 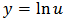 we obtain,
we obtain, 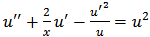 . Now choosing,
. Now choosing, 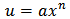 then
then 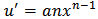 and
and 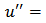
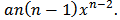 Substitution in equation leads to
Substitution in equation leads to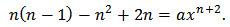 It is clear that this relation can be hold if
It is clear that this relation can be hold if 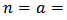
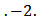 Thus,
Thus, 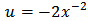 . That is,
. That is, 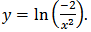 Another procedure that may be used to get a particular solution is to reduce the order of second-order ODEs by a group of transformations. The resulting first-order ODE can be written in the form
Another procedure that may be used to get a particular solution is to reduce the order of second-order ODEs by a group of transformations. The resulting first-order ODE can be written in the form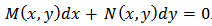 | (3) |
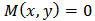 and
and 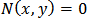 intersect, the intersection points could be helpful to obtain particular solutions. It should be pointed out that this precudre may be useful if such transformatoins could be done and graphs intersect. If so, this procedure can be a general method to solve Eq. (3).We back to Poisson-Boltzman’s equation and rewrite the equation as
intersect, the intersection points could be helpful to obtain particular solutions. It should be pointed out that this precudre may be useful if such transformatoins could be done and graphs intersect. If so, this procedure can be a general method to solve Eq. (3).We back to Poisson-Boltzman’s equation and rewrite the equation as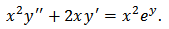 Suppose
Suppose 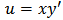 and
and 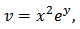 then the equation transforms to
then the equation transforms to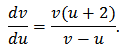 This equation could not be solved analytically, but if we write
This equation could not be solved analytically, but if we write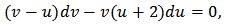 then one may choose
then one may choose 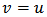 and
and 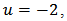 i.e.,
i.e., 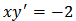 and
and 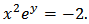 These two relations lead to
These two relations lead to 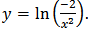 This solution is the same particular solution as we got in previous one. Let us back to Thomas-Fermi’s equation
This solution is the same particular solution as we got in previous one. Let us back to Thomas-Fermi’s equation 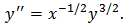 Set
Set 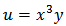 and
and 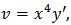 then we obtain
then we obtain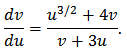 One may write
One may write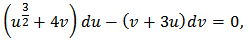 and construct
and construct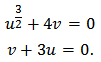 It is not difficult to show that the intersection points are
It is not difficult to show that the intersection points are 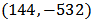 and
and 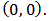 Now if we choose
Now if we choose 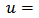
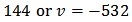 we obtain
we obtain 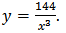
3. Conclusions
- In this study, the particular solutions of some nonlinear ODEs been obtained by two simple procedures. Briefly speaking, these procedures yield extended scope of applicability, simplicity, flexibility in application, and avoidance of complicated numerical and analytical integrations.
ACKNOWLEDGMENTS
- The authors would like to express their thanks to Dr O. Jalili, (Islamic Azad University, Nour Branch), for his valuable comments and suggestions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML