-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2014; 4(6): 187-191
doi:10.5923/j.ajcam.20140406.01

Fractional Fourier Series with Applications
Abu Hammad I. , Khalil R.
University of Jordan, Jordan
Correspondence to: Khalil R. , University of Jordan, Jordan.
| Email: |  |
Copyright © 2014 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, we introduce conformable fractional Fourier series. We use such series to solve certain partial fractional differential equations.
Keywords: Fractional fourier series, Conformable fractional derivative
Cite this paper: Abu Hammad I. , Khalil R. , Fractional Fourier Series with Applications, American Journal of Computational and Applied Mathematics , Vol. 4 No. 6, 2014, pp. 187-191. doi: 10.5923/j.ajcam.20140406.01.
Article Outline
1. Introduction
- Fourier series is one of the most important tools in applied sciences. For example one can solve partial differential equations using Fourier series. Further one can find the sum of certain numerical series using Fourier series. Fractional partial differential equations appeared to have many applications in physics and engineering. There are many definitions of fractional derivative. One of the most recent ones is the conformal fractional derivative [5].Recently [1], fractional Taylor power series was introduced, and a beautiful theory was layed there. However, no work is done on fractional Fourier series, though there is some work on fractional fourier transform.The aim of this paper is to introduce conformable fractional Fourier series. As an application we solve some fractional partial differential equations using fractional Fourier series.For more applications on conformable fractional derivative we refer to [2-4].
2. Basics of Conformable Fractional Derivative
- The subject of fractional derivative is as old as calculus. In 1695, L’Hopital asked if the expression
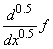 has any meaning. Since then, many researchers have been trying to generalize the concept of the usual derivative to fractional derivatives. These days, many definitions for the fractional derivative are available. Most of these definitions use an integral form. The most popular definitions are:(i) Riemann - Liouville Definition: If
has any meaning. Since then, many researchers have been trying to generalize the concept of the usual derivative to fractional derivatives. These days, many definitions for the fractional derivative are available. Most of these definitions use an integral form. The most popular definitions are:(i) Riemann - Liouville Definition: If 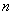 is a positive integer and
is a positive integer and 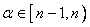 , the αth derivative of f is given by
, the αth derivative of f is given by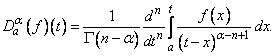 (ii) Caputo Definition. For
(ii) Caputo Definition. For 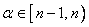 , the α derivative of
, the α derivative of 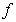 is
is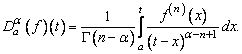 Now, all definitions are attempted to satisfy the usual properties of the standard derivative. The only property inherited by all definitions of fractional derivative is the linearity property. However, the following are the set- backs of one definition or another:(i) The Riemann-Liouville derivative does not satisfy
Now, all definitions are attempted to satisfy the usual properties of the standard derivative. The only property inherited by all definitions of fractional derivative is the linearity property. However, the following are the set- backs of one definition or another:(i) The Riemann-Liouville derivative does not satisfy 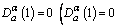 for the Caputo derivative), if α is not a natural number.(ii) All fractional derivatives do not satisfy the known product rule:
for the Caputo derivative), if α is not a natural number.(ii) All fractional derivatives do not satisfy the known product rule: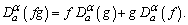 (iii) All fractional derivatives do not satisfy the known quotient rule:
(iii) All fractional derivatives do not satisfy the known quotient rule: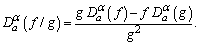 (iv) All fractional derivatives do not satisfy the chain rule:
(iv) All fractional derivatives do not satisfy the chain rule: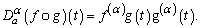 (v) All fractional derivatives do not satisfy:
(v) All fractional derivatives do not satisfy: 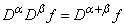 in general(vi) Caputo definition assumes that the function
in general(vi) Caputo definition assumes that the function 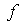 is differentiable.(vii)
is differentiable.(vii) 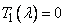 , for all constant functions
, for all constant functions 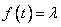 .In a new definition called conformable fractional derivative was introduced.Definition. If α > 0 then we define
.In a new definition called conformable fractional derivative was introduced.Definition. If α > 0 then we define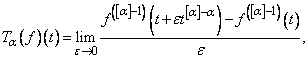 where
where 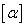 is the ceiling of α. We call
is the ceiling of α. We call 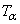 the fractional derivative of
the fractional derivative of 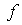 of order α. We shall write
of order α. We shall write 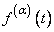 for
for 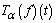 .The new definition satisfies:1.
.The new definition satisfies:1. 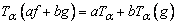 , for all
, for all 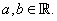 2.
2. 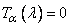 , for all constant functions
, for all constant functions 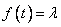 .Further, for
.Further, for 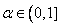 and
and 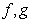 be α-differentiable at a point
be α-differentiable at a point 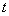 , with
, with 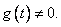 Then3.
Then3. 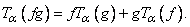 4.
4. 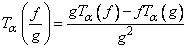 We list here the fractional derivatives of certain functions, for the purpose of comparing the results of the new definition with the usual definition of the derivative:1. 2.1.
We list here the fractional derivatives of certain functions, for the purpose of comparing the results of the new definition with the usual definition of the derivative:1. 2.1. 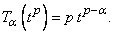 2.2.
2.2. 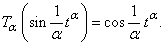 2.3.
2.3. 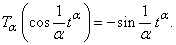 2.4.
2.4. 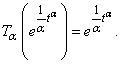 On letting
On letting 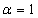 in these derivatives, we get the corresponding ordinary derivatives.One should notice that a function could be α-differentiable at a point but not differentiable, for example, take
in these derivatives, we get the corresponding ordinary derivatives.One should notice that a function could be α-differentiable at a point but not differentiable, for example, take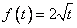 . Then
. Then 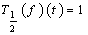 . Hence
. Hence 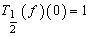 . But
. But 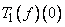 does not exist. This is not the case for the known classical fractional derivatives.
does not exist. This is not the case for the known classical fractional derivatives.3. Fractional Fourier Series
- Let
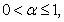 and
and 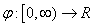 be defined by
be defined by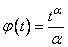 and
and 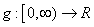 be any function. Let
be any function. Let 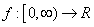 be defined by
be defined by 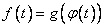 For example, if
For example, if 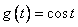 , then
, then 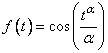 Definition 3.1. A function
Definition 3.1. A function 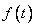 is called α-periodical with period
is called α-periodical with period 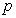 if
if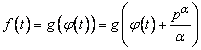 for all
for all 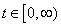 As an example,
As an example, 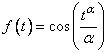 is α-periodic with period
is α-periodic with period 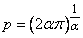 Definition 3.2. Two functions
Definition 3.2. Two functions 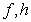 are called α-orthogonal on
are called α-orthogonal on 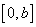 if
if 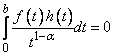 Examples 3.1.
Examples 3.1. 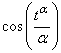 and
and 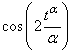 are α-orthogonal on
are α-orthogonal on  .Proof. Put
.Proof. Put 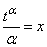 . Then
. Then 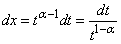 Further, when t = 0, x = 0, and when
Further, when t = 0, x = 0, and when 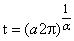 , x = 2π. Hence
, x = 2π. Hence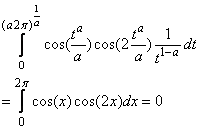 In general, using the idea in example 3.1 one can easily prove:Theorem 3.1. (i)
In general, using the idea in example 3.1 one can easily prove:Theorem 3.1. (i) 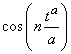 and
and 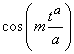 are orthogonal on
are orthogonal on 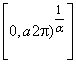 , for all n ≠ m.(ii)
, for all n ≠ m.(ii) 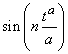 and
and 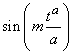 are orthogonal on , for all n ≠ m.(iii)
are orthogonal on , for all n ≠ m.(iii) 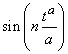 and
and 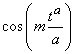 are orthogonal on
are orthogonal on 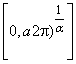 , for all n, m.Now let us define the Fourier coefficients of an α-periodic function with period p.Definition 3.3. Let f:
, for all n, m.Now let us define the Fourier coefficients of an α-periodic function with period p.Definition 3.3. Let f: 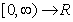 be a given peicewise continuous α-periodic with period p: Then we define:(i) The cosine α-Fourier coefficients of f as
be a given peicewise continuous α-periodic with period p: Then we define:(i) The cosine α-Fourier coefficients of f as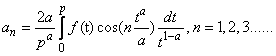 (ii) The sine α-Fourier coefficients of f as
(ii) The sine α-Fourier coefficients of f as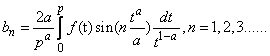 For example, the cosine
For example, the cosine 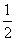 -Fourier coefficients of the function
-Fourier coefficients of the function 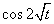 is: a1 = 1, and an = 0 for all n ≠ 1, where
is: a1 = 1, and an = 0 for all n ≠ 1, where 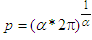 ,
, 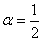 .Now, we give the definition of the fractional Fourier series:Definition 3.4. Let f:
.Now, we give the definition of the fractional Fourier series:Definition 3.4. Let f: 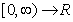 be a given peicewise continuous function which is α-periodical with period p: Then the α-fractional Fourier series of f associated with the interval [0, p] is
be a given peicewise continuous function which is α-periodical with period p: Then the α-fractional Fourier series of f associated with the interval [0, p] is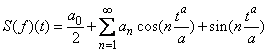 where an and bn are as in Definition 3.3Let us have some examples.Example 3.2. Let
where an and bn are as in Definition 3.3Let us have some examples.Example 3.2. Let 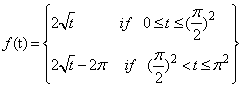 , and
, and 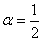 ,with p = π2 on the interval [0, π2]: Then,
,with p = π2 on the interval [0, π2]: Then,
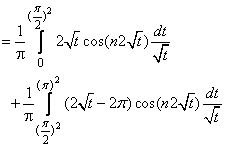 Using change of variables:
Using change of variables: 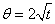 , we get
, we get 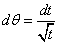 , θ = 0 if t = 0, t = 0, θ = πif
, θ = 0 if t = 0, t = 0, θ = πif 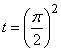 , and θ = 2π if t = (π)2. Hence, the integral becomes
, and θ = 2π if t = (π)2. Hence, the integral becomes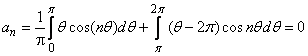 Similarly
Similarly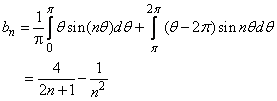 So,
So,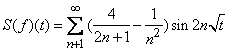 Example 3.3. Let
Example 3.3. Let 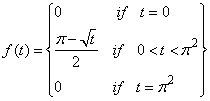 Then
Then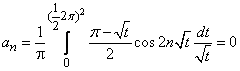 and
and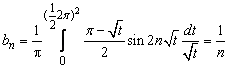 Hence
Hence 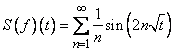 One can easily prove the following classical result.Theorem 3.2. The fractional Fourier series of a piece wise continuous α- periodical function converges pointwise to the average limit of the function at each point of discontinuity, and to the function at each point of continuity.
One can easily prove the following classical result.Theorem 3.2. The fractional Fourier series of a piece wise continuous α- periodical function converges pointwise to the average limit of the function at each point of discontinuity, and to the function at each point of continuity.4. Applications
- In this section we will use fractional Fourier series to solve some fractional partial differential equations. Namely, we will solve the equation
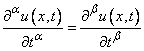 | (4.1) |
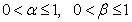 | (4.2) |
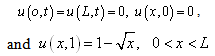 | (4.3) |
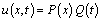 . Substitute in the equation to get
. Substitute in the equation to get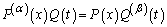 From which we get
From which we get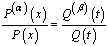 Since x and t are independent variables, then we get
Since x and t are independent variables, then we get  , constant to be determined. Hence
, constant to be determined. Hence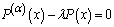 | (4.4) |
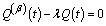 | (4.5) |
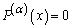 , and from the property (2) of conformable fractional derivative, we get
, and from the property (2) of conformable fractional derivative, we get 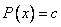 . Condition (4.3) shows that c = 0:(ii) λ > 0. Then equation (4.4) becomes
. Condition (4.3) shows that c = 0:(ii) λ > 0. Then equation (4.4) becomes 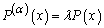 , and from formula (2.4) of the conformable fractional derivative, we get
, and from formula (2.4) of the conformable fractional derivative, we get 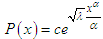 . Condition (4.3) shows that c = 0:(iii) λ < 0. Then equation (4.4) becomes
. Condition (4.3) shows that c = 0:(iii) λ < 0. Then equation (4.4) becomes 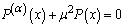 . Using formulas (2.2) and (2.3) we get
. Using formulas (2.2) and (2.3) we get 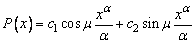 | (4.6) |
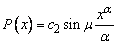 . Another use of condition (4.3) gives
. Another use of condition (4.3) gives 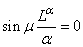 . Hence
. Hence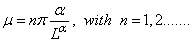 | (4.7) |
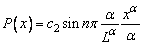 | (4.8) |
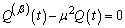 . Using formula (2.4) we get
. Using formula (2.4) we get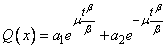 | (4.9) |
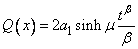 | (4.10) |
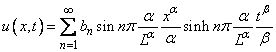 | (4.11) |
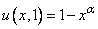 , to get
, to get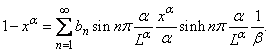 Using the α - Fourier series of 1 - xα, we find bn
Using the α - Fourier series of 1 - xα, we find bn Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML