1. Introduction

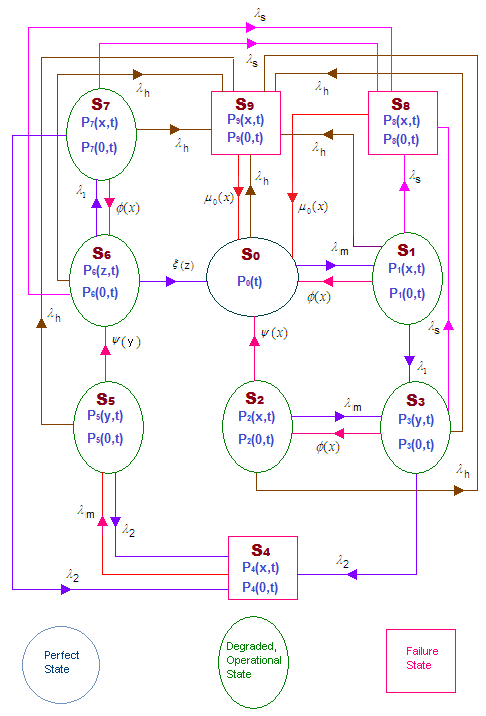
Earlier, the researchers and scientists, who studied the reliability characteristics of repairable complex system, proclaimed their validation of the results in the field of reliability by taking different failure rates and one repair. Most of the researchers assumed that the failed unit can be repaired by a single repairman. Thus, whenever the system / subsystem fails, one type of repair is employed to repair the system, which takes more times for repair the failed unit, resulting the industry /organization suffered with a great loss. The authors in [2, 12, 13, 22] studied the reliability characteristic of a complex systems under and preemptive resume repair policy using copula distribution. The researchers in [4, 5, 11, 15] studied availability of complex system with common cause failure and reliability of duplex standby system by supplementary variable technique [6] and Laplace transform. In case, an ordinary repair facility is employed to repair a failed unit, it will have a great impact on functioning of industry / organization, resulting the organization may suffered a great loss and the manufacturer will lose own market reputation. Human failure arises in the system due to wrongly operation by untrained or inexperience operator. Appearance of human failure completely breakdown the system and can damage many important parts of the system. In this context the authors in [3] studied the automation scenario analysis of human and system reliability under different types failure and general repair policy. Availability of system define the reliability that the system will perform its intended work over a period of time when the repair is available. Thus unavailability is the probability that the system is not able to perform intended task. The authors in [8] studied unavailability analysis of safety system under aging supplementary variable technique and Laplace transform. The authors in [18] studied a complex system by considering interesting modeling of system which having three units at super priority, priority and ordinary under preemptive resume repair policy employing supplementary variable technique and Laplace transform.

We observed, in many situations in real life, where more than one repair is possible between two adjacent transition states, the system is repaired by copula distribution [10, 16], which couples the general and exponential distribution. If the main unit of system fails, the standby unit starts performing the task of the failed unit. The system could be repaired by employing general repair, by the repairman with his own capability but whenever the system is in complete failure mode, it should be repaired by employing Copula (Gumbel-Hougaard family copula) distribution. Using this strategy, the authors in [7, 14, 17, 19] studied the reliability characteristics of complex systems, which consist of two subsystems with controller and standby complex system with waiting repair policy using Gumbel-Hougaard family copula distribution. The automatic controlled switch play an important role in improvement the reliability of a repairable system. The prime aim in any industry or organization is to gain more profit with least expenditure. Therefore, when the system is in operational mode via standby unit, it should be repaired by ordinary repair facility and whenever the system is in completely breakdown mode, it should be repaired by copula. Recently the authors in [20, 21] studied the reliability measures of a standby complex system with different types of failure under waiting repair discipline using Gumbel-Hougaard family Copula distribution by considering two types of failures i.e. partial failure (minor and major) and complete failure. Either earlier the researchers ignored the concept of switch failure or the concept of general repair policy had employed to repair the failed unit / subsystems.

Therefore, in this paper, we have paid our attention on the study of complex system, which consists of two standby redundant units under the concept of an auto-cut switch and human failure. We have analyzed the system for different situation where the systems have one standby unit, ignoring the switch failure and the human failure. Initially, the main unit starts functioning and on failure of main unit, the first standby unit takes its load and the available repairer starts repairing the failed unit. In case the failed unit repaired before failure of standby unit, it takes load of standby unit and the standby unit goes for standby mode. If the first standby unit fails before repair of main unit then second standby unit takes load of first standby unit and repair in continuous will be given to main failed unit. If main unit is repaired before the failure of second standby unit, it start functioning due to auto cut device, repair is assigned to first failed unit and then to second unit. Thus the main unit will never will be in non-operational mode, it will be in either operational mode or under repairing. The system will be in completely failure mode in the following situations: 1) both standby units fail before repairing of the main unit, 2) Switch fails at any instant during operational mode, 3) The human failure occurs at any stage when the system is in operational mode. Human operator operates the system; the human error can arise at any stage when the system is in operational mode.

All failure rates are assumed to be constants and follows exponential distribution, but the repair follows two types of distribution namely: General distribution and Gumbel-Hougaard family copula distribution. Whenever the system is in partially failed state [S₁, S₂, S₃, S₄, S₅, S₆, S₇] of Fig. 2, the general repair is employed but whenever the system is in completely failed state [ S₈, S₉] of Fig. 2, it is repaired by Gumbel-Hougaard family copula distribution.

The researchers mainly paid their attention for the study of some traditional measures including reliability, availability, MTTF and cost analysis which have been studied earlier by varies investigators, using various methods. The study of reliability engineering in not only sufficient up to these measures, but still there are many measures, whose study is also required in the field of reliability theory. This needs study of sensitivity analysis for various measures as demanded by various industries & organizations. Hence fore in the present paper, we have discussed the sensitivity of reliability and MTTF, including the traditional measures.

The paper is organized as follows: Section 2 explains the description of mathematical model. Section 3 describes the formulation and solution of mathematical model. The section 4 describes the MTTF of the system. Section 5 sensitivity analysis of reliability and MTTF of described model. Finally, section 6 of the paper describes the interpretation and conclusion of the paper.

2. Mathematical Model Description

2.1. State Description for Mathematical Model

Table 1. State Description for Mathematical Model of Fig. 2

The description of states conclude that in state S₀ the system is in perfect state where main unit and both redundant unit and auto cut switch is in good working condition. S₁, S₂, S₃, S₅, S₆, S₇, are the states where the system is in degraded mode and the repair is being employed, states S₄, S₈, and S₉ are the states where the system is in completely failure mode.

2.2. Nomenclature

Table 2. Parameters and Symbols used in Analysis of Model

2.3. Assumption

The following assumptions are taken throughout the discussion of the model:

Initially in S₀ state and all units as well as switch of system is in good working condition.

The system works successfully till redundant units are is in working condition.

The system fails if both redundant units fail before repair of main unit.

The switch is instaleous and auto cut it did not take time for switching to redundant unit.

The system can be repaired when it is in degraded state or completely failed state.

All failure rates are constant and they follow an exponential distribution.

Human failure /complete failure& switch failure of the system needs immediate repairing, there for it is repaired by Gumbel-Hougaard family copula.

It is assumes that repaired system works like a new system and there will be no damage done due to repair.

As soon as the failed unit gets repair it ready to perform the task with full efficiency.

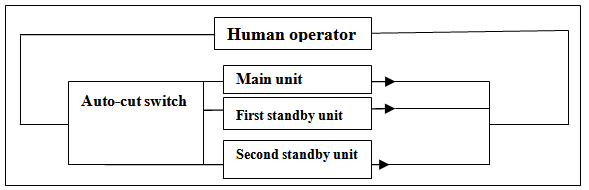
2.4. System Configuration

Figure 1. System Configuration of Model

2.5. State Transition Diagram of Model

Figure 2. Transition State Diagram of Model

3. Formulation and Solution of Mathematical Model

3.1. Mathematical Formulation of Model

By the probability of considerations and continuity of arguments, we can obtain the set of difference differential equations governing the present mathematical model as shown in appendix 1.

Appendix 1. should be here:

Solving (21)-(29), with help of equations (30) to (38)

one may get,

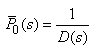(39)

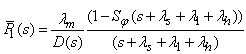(40)

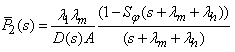(41)

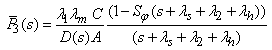(42)

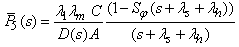(43)

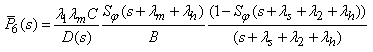(44)

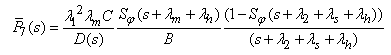(45)

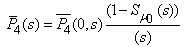(46)

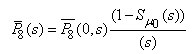(47)

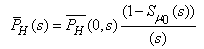(48)

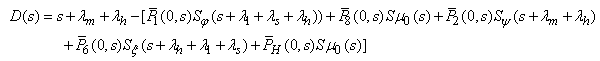Where,

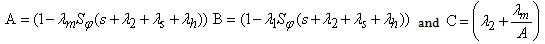The Laplace transformations of the probabilities that the system is in up (i.e. either good or degraded state) and failed state at any time is as follows:

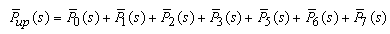(49)

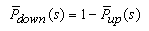(50)

3.2. Particular Cases

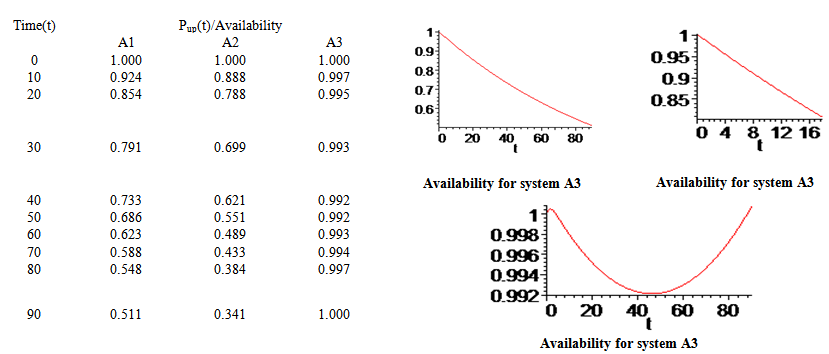
A. Availability Analysis: For particular cases the study of availability is focus on following cases,

A1. Availability (Availability of system), A2. Availability (Switch is ignore) & A3. Availability (Human failure is ignore);

When repair follows exponential distribution, setting

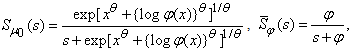taking the values of different parameters as λ_m=0.03, λ₁=0.02, λ₂ = 0.015, λ_h = 0.012, λ_s = 0.025, 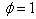, θ = 1, x = 1, in (49), then taking the inverse Laplace transform, one can obtain,

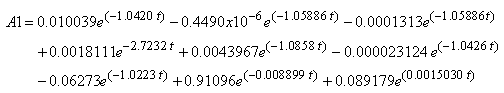(51A1)

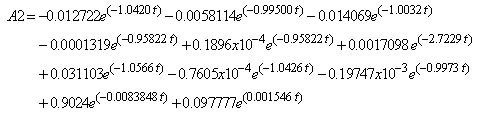(51A2)

(51A3)

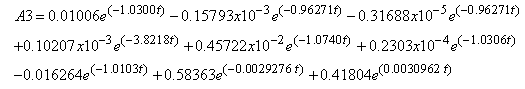For, t= 0, 10, 20, 30, 40, 50, 60, 70, 80, 90; units of time, one may get different values of P_up(t) with the help of (51 A1), (51 A2)& (51 A3) as shown in Fig. 3.

Figure 3. Availability as function of time

B. Reliability Analysis: Taking all repair equal to zero in equation (47) and taking inverse Laplace transform, one can have expression for the reliability of system and for given values of failure rates λ_m=0.03, λ₁=0.02, λ₂ = 0.015, λ_h = 0.012, λ_s = 0.025, in (49), we get (52)a and (52)b;

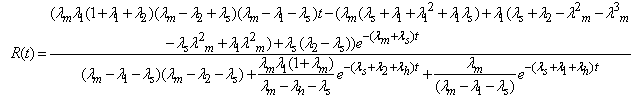(52a)

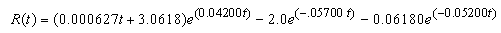(52b)

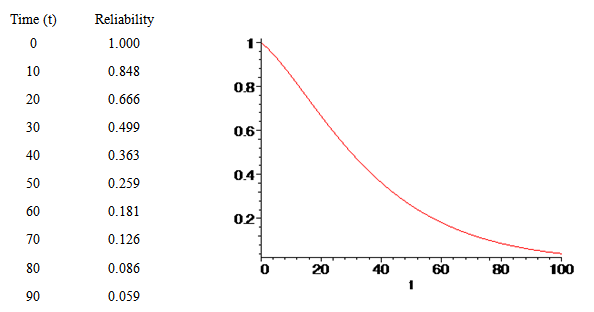Figure 4. Reliability as function of time

4. Mean Time to Failure (MTTF)

Taking all repairs zero and the limit as s tends to zero in (49) for the exponential distribution; one can obtain the MTTF as:

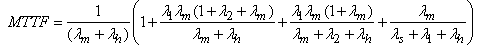(53)

Setting λ_m=0.03, λ₁=0.02, λ₂=0.015, λ_s=0.025, λ_h=0.012 and varying λ_m, λ₁, λ₂, λ_s, λ_h one by one respectively as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09 in (53), one may obtain the variation of M.T.T.F. with respect to failure rates as shown in Fig.4.

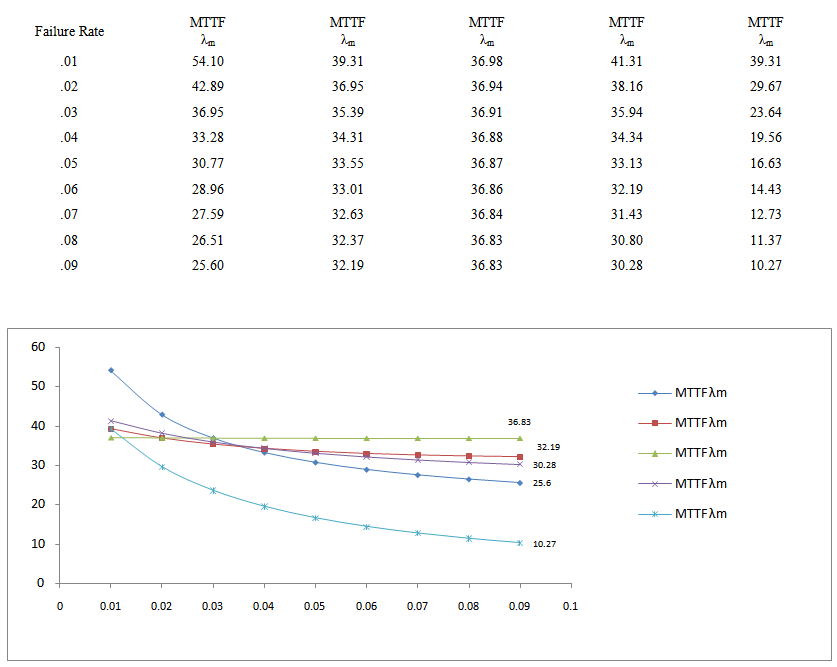Figure 5. MTTF as function of Failure rate

Table 6. Sensitivity of reliability as a function of time

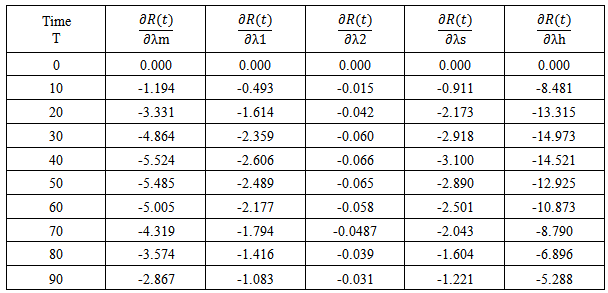
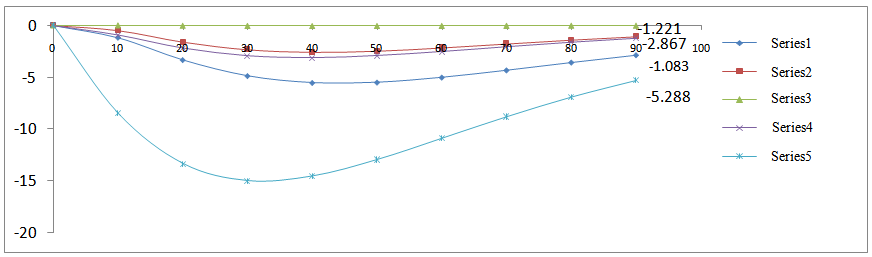Figure 6. For sensitivity of reliability as a function failure rates

Table 7. Sensitivity of MTTF as a function of failure rates

5. Sensitivity Analysis

5.1. Sensitivity of Reliability

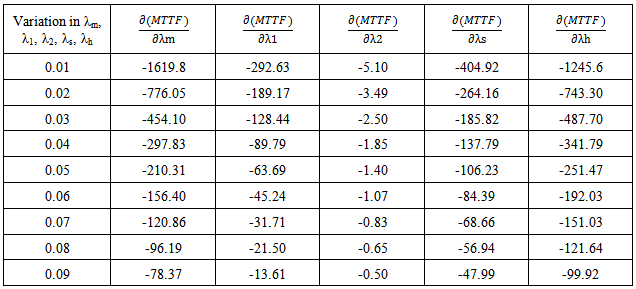
The sensitivity of the reliability can be characterize as the rate of change of reliability with respect to input factor, most regularly defined as the partial derivative of reliability with respect to failure rates. Thus, the sensitivity of reliability and MTTF can be defined as the rate of variation of outcome measure with respect to input factor. There for the sensitivity of reliability can be obtain by differentiating the (52a) and (52 b) with respect to λ_m, λ₁, λ₂, λ_s, λ_h., and setting λ_m=0.03, λ₁=0.02, λ₂ = 0.015, λ_h = 0.012, λ_s = 0.025 one can obtain Table 6 and Figure 6, respectively for sensitivity of reliability. Sensitivity of MTTF can be obtained by making partial derivative of MTTF with respect to failure rates. Results are highlighted as in Table and corresponding Figure.7 respectively.

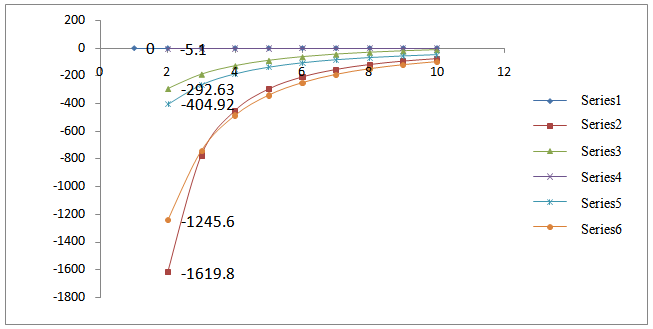Figure 7. Sensitivity of MTTF as a function of failure rates

5.2. Sensitivity of MTTF

Sensitivity analysis for change in MTTF resulting from changes in the system parameters i.e. system failure rates λ_m, λ₁, λ₂, λ_s, λ_h. By differentiating Equation (51) with respect to failure rates λ_m, λ₁, λ₂, λ_s, λ_h respectively one get values of

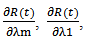
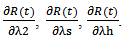
6. Cost Analysis

Let the service facility be always available, then expected profit during the interval [0, t) is;

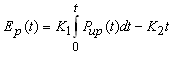(54)

For the same set of parameter of (47), one can obtain (52). Therefore

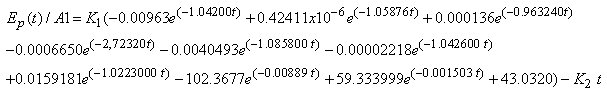(54A1)

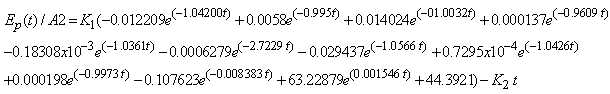(54A2)

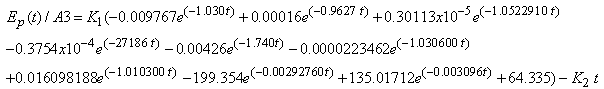(54A3)

Setting K₁= 1and K₂= 0.5, 0.25, 0.15, 0.10 and 0.05 respectively and varying t =0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 units of time, the results for expected profit can be obtain as shown in Fig.5.

Table 8. For expected profit Time(t) Ep(t) A1 Ep(t) A2 Ep(t) A3 Ep(t)/A1; K2=0.5 Ep(t)/A1; K2=0.25 Ep(t)/A2; K2=0.5 Ep(t)/A2; K2=0.25 Ep(t)/A3; K2=0.5 Ep(t)/A3; K2=0.05 0 0 0 0 0 0 0 10 4.61 7.11 4.64 7.14 5.00 7.50 20 8.50 13.50 8.60 13.60 9.96 14.96 30 11.72 19.22 11.94 19.44 14.90 22.40 40 14.33 24.33 14.70 24.70 19.83 29.83 50 16.39 28.89 16.94 29.44 24.75 37.25 60 17.95 32.95 18.92 33.69 29.68 44.68 70 19.04 36.54 20.00 37.51 34.61 52.11 80 19.71 39.71 20.92 40.92 39.57 59.11 90 20.00 42.50 21.46 43.96 44.56 66.06 100 19.95 44.95 21.66 46.66 49.59 74.59

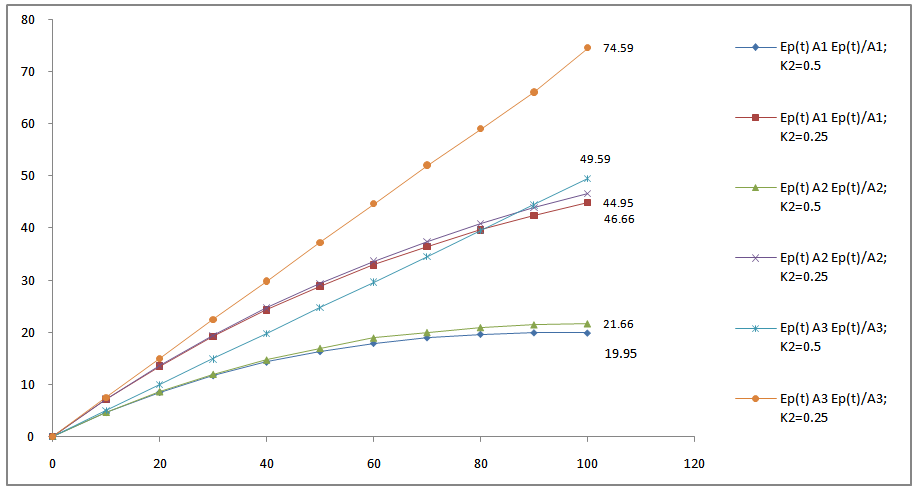Figure 8. Expected profit as function of time

7. Interpretation of Results and Conclusions

Fig.3 provides information how the availability of the complex repairable system changes with respect to the time when failure rates are fixed at different values. When failure rates are fixed at lower values λ_m = 0.03, λ₁ = 0.02, λ₂ = 0.015, λ_s = 0.025, λ_h = 0.012, availability of the system decreases and ultimately becomes steady to the value zero after a sufficient long interval of time. Hence, one can safely predict the future behavior of a complex system at any time for any given set of parametric values, as is evident by the graphical consideration of the model. Availability of system for which human failure is ignored is decreases up to time t=60, but it again start increasing again. In figure.4 provides the variation in reliability of non-repairable system. Fig. 5, yields the mean-time-to-failure (M.T.T.F.) of the system with respect to variation in λ_m, λ₁, λ₂, λ_s, and λ_h respectively when the other parameters have been taken as constant. The variation in MTTF corresponding to failure rates λ_s, λ_p are almost is very closure but corresponding to λ_B, λ_h the variation is very high which indicates that these both are more responsible to proper operation of the system. The measure of sensitivity of reliability and MTTF has discussed in section C of paper which rate of change of the value of output variable with change of output variable. When revenue cost per unit time K₁ is fixed at 1, service costs K₂ = 0.5, 0.25, 0.15, 0.10, 0.05, profit has been calculated and results are demonstrated by graphs in Fig.8. A critical examination from Fig.8 reveals that expected profit increases with respect to the time when the service cost K₂ fixed at minimum value 0.05. Finally, one can observe that as service cost increase, profit decrease. In general, for low service cost, the expected profit is high in comparison to high service cost.

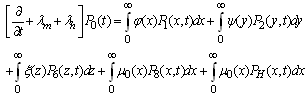(1)

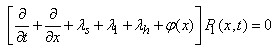(2)

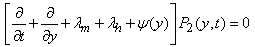(3)

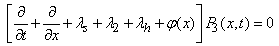(4)

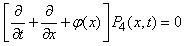(5)

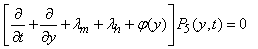(6)

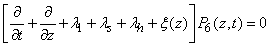(7)

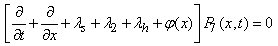(8)

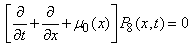(9)

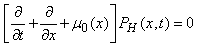(10)

Boundary conditions

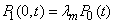(11)

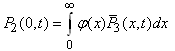(12)

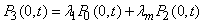(13)

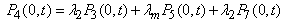(14)

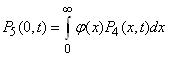(15)

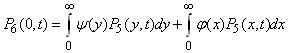(16)

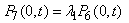(17)

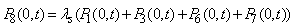(18)

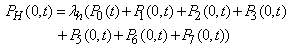(19)

B. Solution of the model

Taking Laplace transformation of equations (1)-(19) and using equation with help of initial condition, P₀(t)=1 and other state probabilities are zero at t

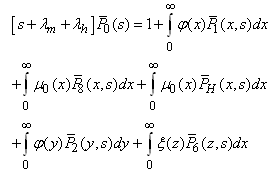(20)

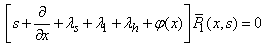(21)

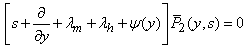(22)

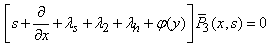(23)

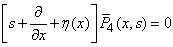(24)

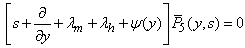(25)

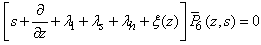(26)

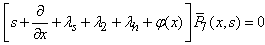(27)

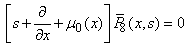(28)

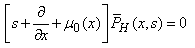(29)

Laplace transform of boundary conditions

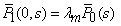(30)

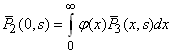(31)

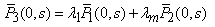(32)

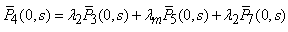(33)

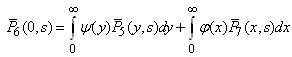(35)

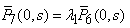(36)

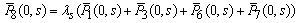(37)

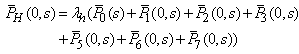(38)