Abubakar A.1, Taiwo O. A.2
1Department of Mathematics and Computer Science, Ibrahim Badamasi Babangida University, Lapai. Niger State, Nigeria
2Department of Mathematics, University of Ilorin, Ilorin, Nigeria
Correspondence to: Taiwo O. A., Department of Mathematics, University of Ilorin, Ilorin, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we employed the use of Standard Integral Collocation ApproximationMethod to obtain numerical solutions of special higher orders linear Fredholm-Volterra Integro-Differential Equations. Power Series, Chebyshev and Legendre's Polynomials forms of approximations are used as basis functions. From the computational view points, the method is efficient, convenient, reliable and superior to many existing methods. Two examples each of first and second orders and one of third order linear Fredholm - Volterra Integro-Differential Equations are considered to illustrate the method. We observed from the results obtained that the method performed better when compared with the results obtained in Mustafa and Yalcin (2012).
Keywords:
Fredholm-Volterra integro-differential equations, Chebyshev polynomials, Standard integral collocation method
Cite this paper: Abubakar A., Taiwo O. A., Integral Collocation Approximation Methods for the Numerical Solution of High-Orders Linear Fredholm-Volterra Integro-Differential Equations, American Journal of Computational and Applied Mathematics , Vol. 4 No. 4, 2014, pp. 111-117. doi: 10.5923/j.ajcam.20140404.01.
1. Introduction
Integro-Differential Equations have been discussed in many applied fields such as Biology, Physical and Engineering problems. These equations are either Fredholm or Volterra or Fredholm- Volterra Integro Differential Equations are contained in many mathematical formulations of physical phenomena.Therefore, their numerical treatment is desired. .Although, it is generally difficult in finding exact solutions of Fredholm- Volterra Integro Differential Equations (FVIDE) especially when it is nonlinear. Several numerical methods have been used to solve FVIDE among them are Approximation Method (Ezzati and Najafalizadeh, 2011) and (Salih and Mehemet, 2000). Meanwhile, in recent years, the matrix method has been developed to solve Fredholm - Volterra Integral Equations For example, the method is used to solve system of Differential Equations (Akyuz and Sezer, 2003) and Differential Algebraic Equation (Karamete and Sezer, 2002). Other methods include Block Pulse function and Operational Matrices (Leyla, Bijan and Mohammed, 2011), Chebyshev polynomials approach is used in (Yuksel, Gulsu and Sezer, 2012) to mention just a few. In this research work, the work and idea of (Aliyu, 2012) is revisited and modified as our new proposed numerical method to solve the nth order linear Fredholm-Volterra Integro-Differential Equations. The general nth order linear Volterra - Fredholm Integro Differential Equations considered in this work are in two types given as: | (1) |
And,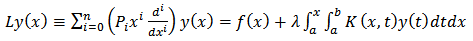 | (2) |
Thus, equation (1) contains disjoint integrals while equation (2) contains mixed integrals. Here, both equations (1) and (2) are subjected to the conditions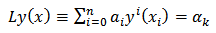 | (3) |
In equations (1), (2) and (3),  are real numbers,
are real numbers, 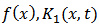 and
and 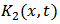 are known given smooth functions and
are known given smooth functions and  is the unknown function to be determined.For the purpose of our discussion, we let
is the unknown function to be determined.For the purpose of our discussion, we let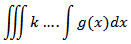 denote the indefinite integration applied to
denote the indefinite integration applied to 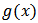 k-times and is denoted by
k-times and is denoted by 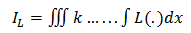 | (4) |
2. Description of Numerical Method of Solution
In this section, we discussed Standard Integral Collocation Method to solve equations (1) and (2) using the following basis functions:* Power Series* Chebyshev Polynomials* Legendre's PolynomialsThis method used the idea reported in (Aliyu, 2012) as applied to solve non over determined differential equation. The method was proposed and used by (Taiwo and Abubakar, 2013) to find numerical solutions to first and second orders linear and non-linear integro-differential equations.
2.1. Method of Solution by Power Series
In order to apply this method, we integrated both sides of equation (1) to have: | (5) |
This implies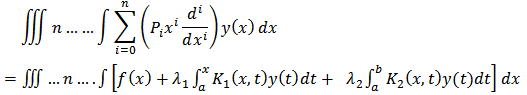 | (6) |
We assumed an approximate solution of the form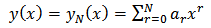 | (7) |
Thus, equation (7) is substituted into equation (6) to have | (8) |
This implies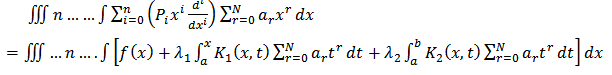 | (9) |
Thus, we collocated equation (9) at the point  to obtain
to obtain | (10) |
Where,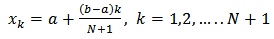 | (11) |
Thus, equation (11) gives (N+1) algebraic linear system of equations in (N+1) unknown constants 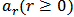 . These (N+1) algebraic linear system of equations are then solved by Gaussians Elimination Method to obtain the unknown constants
. These (N+1) algebraic linear system of equations are then solved by Gaussians Elimination Method to obtain the unknown constants  which are then substituted back into equation (7) to obtain the approximate solution for case N. (the degree of the approximant)REMARK: 1:We demonstrated this method further by choosing n = 1, thus, putting n = 1 in equation (1), we have:
which are then substituted back into equation (7) to obtain the approximate solution for case N. (the degree of the approximant)REMARK: 1:We demonstrated this method further by choosing n = 1, thus, putting n = 1 in equation (1), we have: | (12) |
We integrated equation (12) to have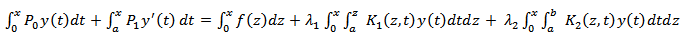 | (13) |
This implies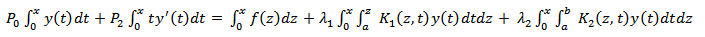 After simplification, we have
After simplification, we have | (14) |
Substituting the approximate solution given in equation (7) into (14), we have This implies,
This implies,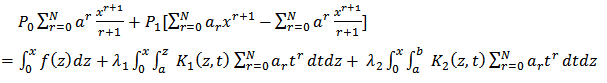 Further simplification gives
Further simplification gives This implies,
This implies, | (15) |
Where,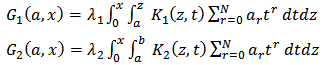 And,
And, 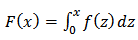 Thus from equation (14), we have
Thus from equation (14), we have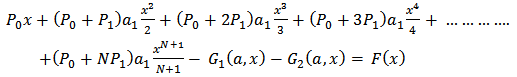 | (16) |
Thus, equation (16) is collocated at the point 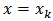 to have
to have 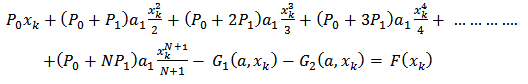 | (17) |
Where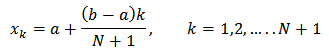 Thus, equation (17) is put in matrix form as
Thus, equation (17) is put in matrix form as Where,
Where, 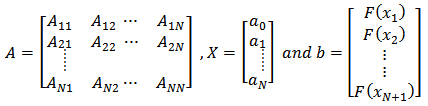 Where,
Where,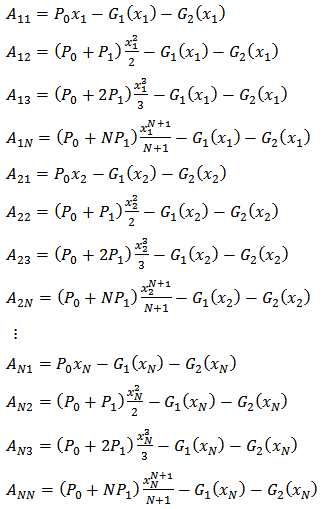 Remark 2:The above matrix is solved by Gaussian Elimination Method to obtain the unknownConstants
Remark 2:The above matrix is solved by Gaussian Elimination Method to obtain the unknownConstants 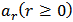 which are then substituted back into the approximateSolution given in equation (7) to obtain the approximate solution for case N.
which are then substituted back into the approximateSolution given in equation (7) to obtain the approximate solution for case N.
2.2. Method of Solution by Chebyshev Polynomials
We demonstrated this method by assuming the approximate solution of the form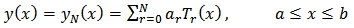 | (18) |
Where,  are unknown constants and
are unknown constants and 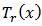 are the Chebushev Polynomial of degrees r of first the kind which is valid in the interval
are the Chebushev Polynomial of degrees r of first the kind which is valid in the interval  and is defined by
and is defined by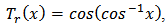 Here,
Here, 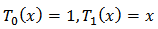 | (19) |
The recurrence relation is given by | (20) |
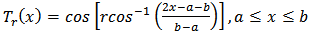 | (21) |
and this satisfies the recurrence relation | (22) |
Substituting equation (18) into equation (6), we have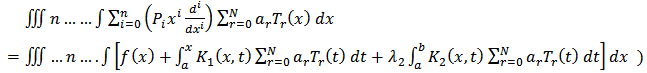 | (23) |
Hence, we collocated (23) at the point  to have
to have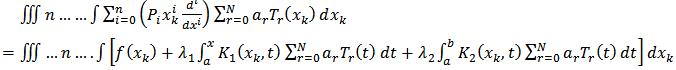 | (24) |
Where 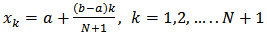 Thus, (24) gives (N + 1) algebraic linear system of equations in (N + 1) unknown constants
Thus, (24) gives (N + 1) algebraic linear system of equations in (N + 1) unknown constants 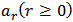 . The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants
. The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants 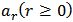 which are then substituted back into equation (18) to obtain the approximate solution for case N.
which are then substituted back into equation (18) to obtain the approximate solution for case N.
2.3. Method of Solution by Legendre’s Polynomials
The Legendre’s Polynomial is denoted and defined by | (25) |
 | (26) |
With, 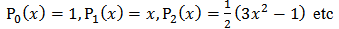 In this method, we assumed an approximate solution of the form
In this method, we assumed an approximate solution of the form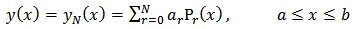 | (27) |
This method is similar to the two methods discussed above (the same procedure discussed as in sections (2.1.1) and (2.1.2)). We have (N + 1) algebraic linear system of equations in (N + 1) unknown constants 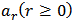 . The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants
. The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants  which are then substituted back intoequation (27) to obtain the approximate solution for case N.
which are then substituted back intoequation (27) to obtain the approximate solution for case N.
3. Numerical Experiment
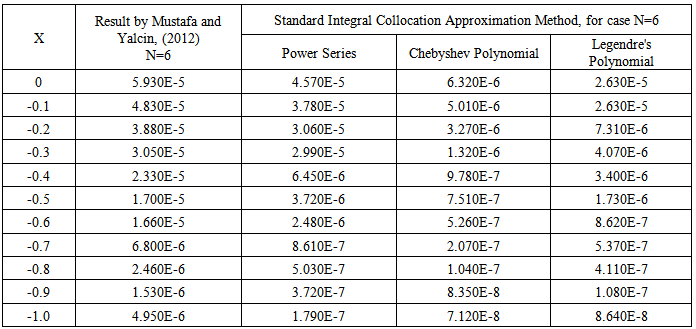
In this section, we have demonstrated the Standard Integral Collocation Approximation Method on first, second and third orders Fredholm - Volterra Integro-Differential Equations using Power series, Chebyshev and Legendre's Polynomials as the basis functions. The examples are solved to illustrate the accuracy, efficiency and time of execution of the method.We have defined absolute error as 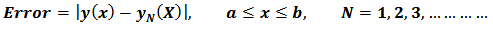 Example 1.We considered first order FVIDE given as
Example 1.We considered first order FVIDE given as 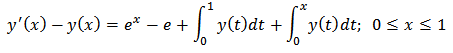 With the mixed condition
With the mixed condition 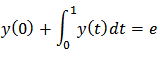 The exact solution is given as
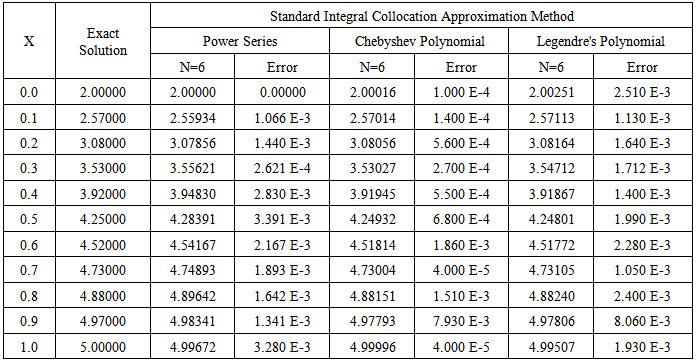
The exact solution is given as  Example 2.We considered second order FVIDE given as
Example 2.We considered second order FVIDE given as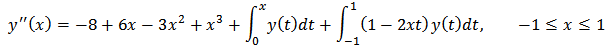 With the conditions
With the conditions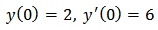 The exact solution is given as
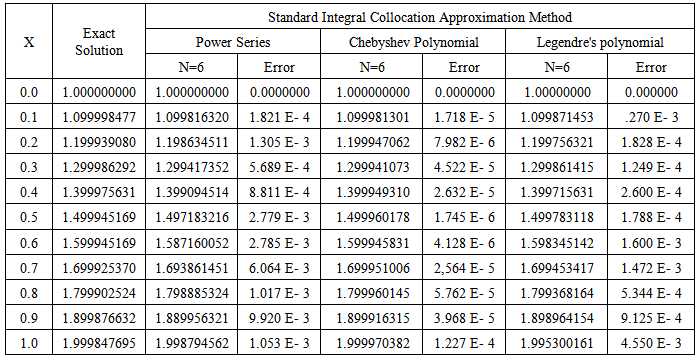
The exact solution is given as  Example 3.We considered the third order FVIDE given as
Example 3.We considered the third order FVIDE given as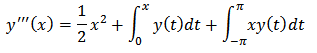 With the conditions
With the conditions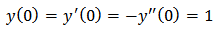 The exact solution is given
The exact solution is given 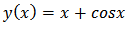
4. Table of Results
Table 1. Numerical results for example 1
 |
| |
|
Table 2. Numerical results for example 2
 |
| |
|
Table 3. Numerical results for example 3
 |
| |
|
5. Conclusions
We have demonstrated Standard Integral Collocation Approximation Method to solve special higher orders linear Fredholm - Volterra Integro Differential Equations by Power Series, Chebyshev and Legendre's Polynomials as the basis functions of approximations. The results obtained by Chebyshev and Legendres's Polynomials as basis functions proved superior than that of power series.However, this method yields the desired accuracy when the results obtained are compared with the exact solutions. The simplicity is an added advantage to the method and hence, it is reliable and a powerful tool for the classes of the problems considered.
References
| [1] | Aliyu, I. M. (2012): A Computational Error Estimation of the Integral Formulation of the Tau Method for Some Class of Ordinary Differential Equations Ph.D.Thesis, (Unpublished), University of Ilorin, Ilorin. |
| [2] | Akyuz, A. and Sezer, M. (2003): Chebyshev polynomial Solutions of System of High Order Linear Differential Equations with Variable Coefficients. Appl. Math. Comput. 144, 237-247. |
| [3] | Arikogulu, A. and Ozkol, I. (2005): Solutions of boundary Value Problems for Integro-Differential Equations by Using Di_erential Transform Method. Appl. Math.Comput 168, 1145-1158 |
| [4] | Asady, B. and Kanjani, M.T. (2005): Direct Method for Solving Integro-Differential Equations Using Hybrid Fourier and Block Functions. Int. J. Computer Math. 82(7), 989-995 |
| [5] | Ezzati, R. and Najafalizadeh, S. (2011): Numerical Solution of Volterra-Fredholm Integral Equation by Using Chebyshev Polynomials. Mathematical Sciences, 5(1):1-12. |
| [6] | Hashim, I. (2006): Adomian Decomposition Method for Solving BVPs for Fourth-Order Integro-Differential Equations. J. Comput. Appl. Math.193:658-664. |
| [7] | Karamete, A. and Sezer, M. (2002): A Taylor Collocation Method for the Solution of Linear Integro-Differential Equations. int. J. Comput. Math. 79(9): 987-1000 |
| [8] | Leyla, R. Bijan, R.and Mohammad, M. (2011): Numerical Solution of Volterra Fredholm Integro-Differential Equation by Block Pulse Functions and Operational Matrices. Gen. Math. Notes, 4(2):37-48. |
| [9] | Malejnejad, K. and Mahmoudi, Y. (2003): Taylor polynomial Solution of Higher-Order Nonlinear Volterra-Fredholm Integro-Differential Equations. Appl. Math.Comput., 155: 317-328. |
| [10] | Mustafa, G. and Yalcin,O. (2012): On Numerical Solution of Linear Fredholm-Volterra Integro-Differential Difference Equations with Piecewise Intervals. Application and Applied Mathematics: An International Journal (AAM), 7: 556-570. |
| [11] | Pachpatte, B. G. (2008): On Volterra and Fredholm Type of Integro-Differential Equations. Tamsui Oxford Journal of Mathematical Science, 24(3): 289-310. |
| [12] | Rabbani, M. and Kiasoltani. S. H. (2011): Solving of Nonlinear System of Fredholm- Volterra Integro-Differential Equations by Using Discrete Collocation Method. The journal of Mathematics and Computer Science, 3(4): 382-389. |
| [13] | Rabbani, M. and Zarali, B. (2012): Solution of Fredholm Integro-Differential Equation System by Modifed Decomposition Method. The Journal of Mathematics and Computer Science, 5(4): 258-264. |
| [14] | Raji, M. T. (2013): Collocation Approximation for Solving Special Linear and Nonlinear Integro-Differential Equations. Ph. D. Thesis, (Unpublished), University of Ilorin, Ilorin, Nigeria |
| [15] | Salih, Y. and Mehmet, S. (2000): The Approximate Solution of Higher Order Linear Volterra-Fredholm Integro- Differential Equations in Term of Taylor Polynomials. Appl.Math. Comput. 112, 291-308. |
| [16] | Taiwo, O. A. and Abubakar, A. (2013): Integral Collocation Approximation Methods for the Numerical Solution of Linear Integro-Differential Equations. IOSR Journal of Mathematics, 8(5): 01-14. |
| [17] | Taiwo, O. A. and Ishola, C. Y. (2009): Collocation Approximation Methods for the Numerical Solution of Integral Equations. Int. Journal Pure and Applied Science, 2,:29-37. |
| [18] | Yuksel, G., Gulsu, M. and Sezer, M. (2012): A Chebyshev Polynomial Approach for Higher-Order Linear Fredholm- Volterra Integro-Differential Equations. Gazi University Journal of Science, 25(2): 393-401. |
| [19] | Wazwaz, A. (2011): Linear and Nonlinear Integral Equations, Methods an Applications. Higher Education Press, Benjing and Springer-Verlag Berlin Heidelberg. |
| [20] | Volk, W. (1985): The Numerical Solution of Linear Integro-Differential Equations by Projection Method. Journal of Integral Equations, 9(1):171-190. |


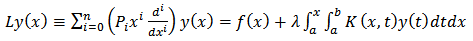
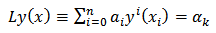
 are real numbers,
are real numbers, 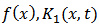 and
and 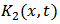 are known given smooth functions and
are known given smooth functions and  is the unknown function to be determined.For the purpose of our discussion, we let
is the unknown function to be determined.For the purpose of our discussion, we let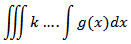 denote the indefinite integration applied to
denote the indefinite integration applied to 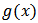 k-times and is denoted by
k-times and is denoted by 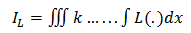

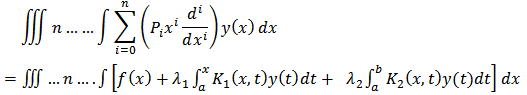
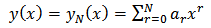

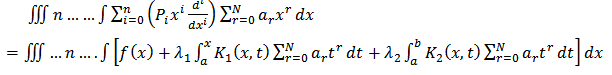
 to obtain
to obtain
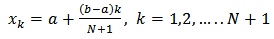
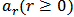 . These (N+1) algebraic linear system of equations are then solved by Gaussians Elimination Method to obtain the unknown constants
. These (N+1) algebraic linear system of equations are then solved by Gaussians Elimination Method to obtain the unknown constants  which are then substituted back into equation (7) to obtain the approximate solution for case N. (the degree of the approximant)REMARK: 1:We demonstrated this method further by choosing n = 1, thus, putting n = 1 in equation (1), we have:
which are then substituted back into equation (7) to obtain the approximate solution for case N. (the degree of the approximant)REMARK: 1:We demonstrated this method further by choosing n = 1, thus, putting n = 1 in equation (1), we have:
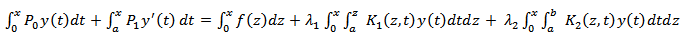
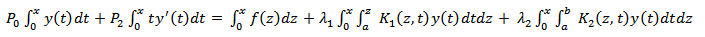 After simplification, we have
After simplification, we have
 This implies,
This implies,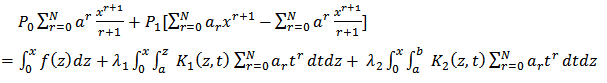 Further simplification gives
Further simplification gives This implies,
This implies,
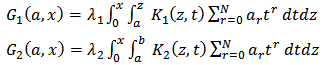 And,
And, 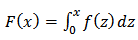 Thus from equation (14), we have
Thus from equation (14), we have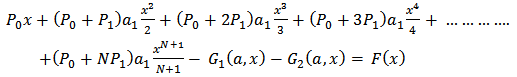
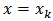 to have
to have 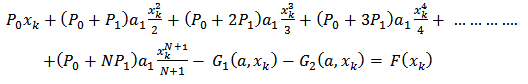
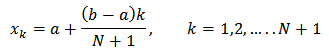 Thus, equation (17) is put in matrix form as
Thus, equation (17) is put in matrix form as Where,
Where, 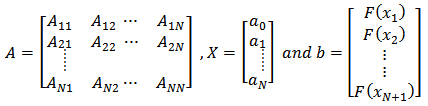 Where,
Where,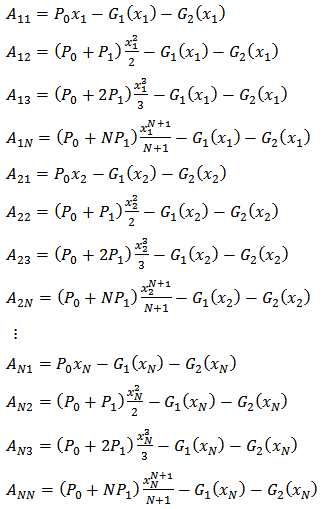 Remark 2:The above matrix is solved by Gaussian Elimination Method to obtain the unknownConstants
Remark 2:The above matrix is solved by Gaussian Elimination Method to obtain the unknownConstants  which are then substituted back into the approximateSolution given in equation (7) to obtain the approximate solution for case N.
which are then substituted back into the approximateSolution given in equation (7) to obtain the approximate solution for case N.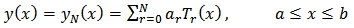
 are unknown constants and
are unknown constants and 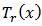 are the Chebushev Polynomial of degrees r of first the kind which is valid in the interval
are the Chebushev Polynomial of degrees r of first the kind which is valid in the interval  and is defined by
and is defined by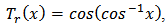 Here,
Here, 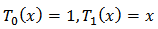

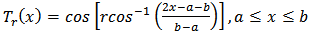

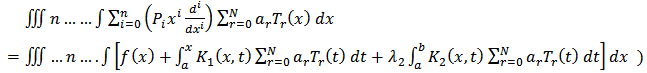
 to have
to have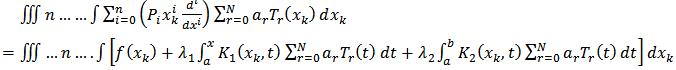
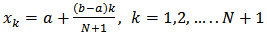 Thus, (24) gives (N + 1) algebraic linear system of equations in (N + 1) unknown constants
Thus, (24) gives (N + 1) algebraic linear system of equations in (N + 1) unknown constants 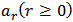 . The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants
. The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants 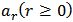 which are then substituted back into equation (18) to obtain the approximate solution for case N.
which are then substituted back into equation (18) to obtain the approximate solution for case N.

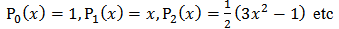 In this method, we assumed an approximate solution of the form
In this method, we assumed an approximate solution of the form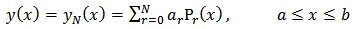
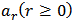 . The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants
. The (N + 1) algebraic system of linear equations are then solved by Gaussian elimination method to obtain the unknown constants  which are then substituted back intoequation (27) to obtain the approximate solution for case N.
which are then substituted back intoequation (27) to obtain the approximate solution for case N.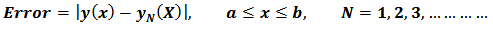 Example 1.We considered first order FVIDE given as
Example 1.We considered first order FVIDE given as 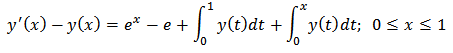 With the mixed condition
With the mixed condition 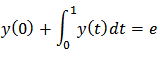 The exact solution is given as
The exact solution is given as  Example 2.We considered second order FVIDE given as
Example 2.We considered second order FVIDE given as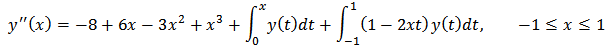 With the conditions
With the conditions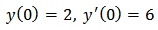 The exact solution is given as
The exact solution is given as  Example 3.We considered the third order FVIDE given as
Example 3.We considered the third order FVIDE given as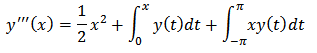 With the conditions
With the conditions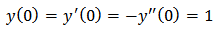 The exact solution is given
The exact solution is given 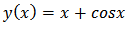
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

