-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2014; 4(3): 97-110
doi:10.5923/j.ajcam.20140403.05
Solving System of Linear Inequalities or Equalities on the Surface of the Unit Shell (LIS-III)
Paul T. R. Wang
WangPaul_Research
Correspondence to: Paul T. R. Wang, WangPaul_Research.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The author presents an innovative concept of a generic algorithm that solves system of homogeneous linear inequalities for finite number of unknowns and constraints utilizing normalized unit vectors of length 1 on the surface of an n-dimensional hyper sphere with a radius of 1 coined as the unit shell and the concept of equal distanced points as sysmmetic points along the arc connecting two equal distanced points to a selected set of points on the unit shell with increasing ranks to locate the desired solution point or points of the given system of linear inequalities if such solution point or points exist. A direct application of this innovative technique applied to a linear program formulated as a system of self-dual homogenerous linear inequalities is illustrated to establish its validity. Furthermore such technique is also illustrated to extend its applicability to solve Differential Variation Inequalities (DVI) over the Unit-Shell. Such a new technique is shown to be extremely efficient, numerical stable, and quite suitable for very large system of linear inequalities with number of variables and/or constraints over millions. In addition, such a new approach does provide insight to solve linear inequalities that is compatible to Gaussian elimination solving linear equalities.
Keywords: Homogeneous Linear Inequalities, Unit-Shell, Liner Programs, Linear Projection and Distance to subspace, n-dimensional normed linear space, and differential variation inequalities
Cite this paper: Paul T. R. Wang, Solving System of Linear Inequalities or Equalities on the Surface of the Unit Shell (LIS-III), American Journal of Computational and Applied Mathematics , Vol. 4 No. 3, 2014, pp. 97-110. doi: 10.5923/j.ajcam.20140403.05.
1. Introduction
- Many years back, the author was working on the hemispherical cover for unit vectors on n-dimensional unit shell as the surface of an unit sphere. If we normalize all row vectors of a linear inequalities system (LIS) in its feasibility form (
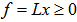 ), they are points on the unit shell of this n-dimensional hyper sphere. Note that
), they are points on the unit shell of this n-dimensional hyper sphere. Note that 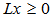 has a solution implies that all the normalized row vectors of
has a solution implies that all the normalized row vectors of 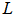 and the normalized solution,
and the normalized solution, 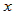 , has a dot product
, has a dot product 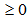 . Hence the hemispherical surface of the unit sphere has a center at
. Hence the hemispherical surface of the unit sphere has a center at 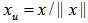 with all points
with all points 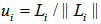 reachable within an arc distance of
reachable within an arc distance of 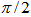 or less. In other words, we have a hemispherical cover
or less. In other words, we have a hemispherical cover  covering all the points of
covering all the points of  . Such a solution of the LIS is also a point on this unit shell as the geometrical center (a point with its maximum arc distance to all the constraint points minimized) of this hemispherical cover. Note that LIS is generic for all linear systems equalities and inequalities are both included. In particular linear programs (LPs) is only a special case of LIS [ref. 17]. The pursuit to locate a unit vector
. Such a solution of the LIS is also a point on this unit shell as the geometrical center (a point with its maximum arc distance to all the constraint points minimized) of this hemispherical cover. Note that LIS is generic for all linear systems equalities and inequalities are both included. In particular linear programs (LPs) is only a special case of LIS [ref. 17]. The pursuit to locate a unit vector  for
for 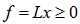 did not succeed then as the geometrical center of a fixed number of points (especially when we are dealing with millions of points!) on a unit shell is very troublesome to locate in n-dimensional hyper space. However, now an effective approach has been identified. Two new insights make such a pursuit feasible and verifiable. First, the concept of “equidistant” for a specific point as an equal distanced point (EDP) to a group of points on the unit shell can be maintained using orthogonal subspace projection. Second, equidistance can be maintained by moving an EDP on the n-dimensional great circle arc connecting two equidistant points with respect to a given set of points. By repeatedly applying this EDP tracking strategy to a set of linearly independent unit vectors with increasing rank as to increase the number of points that are equidistant to the center point as its geometrical center, the solution for the original LIS can easily be located with a minimum number of steps no more than the maximum possible rank of the defining matrix
did not succeed then as the geometrical center of a fixed number of points (especially when we are dealing with millions of points!) on a unit shell is very troublesome to locate in n-dimensional hyper space. However, now an effective approach has been identified. Two new insights make such a pursuit feasible and verifiable. First, the concept of “equidistant” for a specific point as an equal distanced point (EDP) to a group of points on the unit shell can be maintained using orthogonal subspace projection. Second, equidistance can be maintained by moving an EDP on the n-dimensional great circle arc connecting two equidistant points with respect to a given set of points. By repeatedly applying this EDP tracking strategy to a set of linearly independent unit vectors with increasing rank as to increase the number of points that are equidistant to the center point as its geometrical center, the solution for the original LIS can easily be located with a minimum number of steps no more than the maximum possible rank of the defining matrix 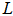 of the LIS. Such a technique is greedy, non-iterative, non-linear, and non-Gaussian, and use only the dot-product operator which is O(n) in operation. No basis vectors swapping is required to minimize the maximum arc distance from a given point to the geometrical center or centers of a set of points on the unit shell. Furthermore, most matrix operations carried out on the unit shell are over unit vectors; hence it is numerical stable avoiding ill-conditioned operations. Consequently, the unit shell approach can be used to resolve problems posted by any liner equalities or inequalities. As result of the perfectly symmetric nature of the unit shell, it can be demonstrated that it requires a minimum number of steps to reach a solution while maintaining numerical stability when it is compared to existing best known algorithms offered by the Simplex or interior point methods. The author illustrates this innovative new technique to solve a simple linear program (LP) system with 7 variables and 14 constraints. Excel is used to carry out such new approach step by step to illustrate and verify its correctness and efficiency. A twist of this approach is that it is capable of solving all the linear systems (equalities, Eigen systems, and inequalities alike) over the unit shell non-linearly! The normalization of vectors on the unit shell also offers numerical stability for ill-conditioned linear systems that are very troublesome to solve with existing techniques in dealing with very large linear systems with millions of variables or constraints. Such an approach may have other applications beyond linear systems such as physics as an alternative to the string theory to resolve the problem of renormalization and operations research NPC mystery (?).The author presents such a geometrical center search strategy for the maximum possible rank with the same number of linearly independent rows in
of the LIS. Such a technique is greedy, non-iterative, non-linear, and non-Gaussian, and use only the dot-product operator which is O(n) in operation. No basis vectors swapping is required to minimize the maximum arc distance from a given point to the geometrical center or centers of a set of points on the unit shell. Furthermore, most matrix operations carried out on the unit shell are over unit vectors; hence it is numerical stable avoiding ill-conditioned operations. Consequently, the unit shell approach can be used to resolve problems posted by any liner equalities or inequalities. As result of the perfectly symmetric nature of the unit shell, it can be demonstrated that it requires a minimum number of steps to reach a solution while maintaining numerical stability when it is compared to existing best known algorithms offered by the Simplex or interior point methods. The author illustrates this innovative new technique to solve a simple linear program (LP) system with 7 variables and 14 constraints. Excel is used to carry out such new approach step by step to illustrate and verify its correctness and efficiency. A twist of this approach is that it is capable of solving all the linear systems (equalities, Eigen systems, and inequalities alike) over the unit shell non-linearly! The normalization of vectors on the unit shell also offers numerical stability for ill-conditioned linear systems that are very troublesome to solve with existing techniques in dealing with very large linear systems with millions of variables or constraints. Such an approach may have other applications beyond linear systems such as physics as an alternative to the string theory to resolve the problem of renormalization and operations research NPC mystery (?).The author presents such a geometrical center search strategy for the maximum possible rank with the same number of linearly independent rows in 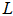 as a solution to
as a solution to 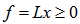 . Such analysis shows that it is possible to solve LIS (linear inequalities system) with non-iterative and non-Gaussian alike algorithms. The author is putting this draft together to highlight this unit shell approach. This approach is coined as LIS-III or Unit Shell for Linear Systems or (US_LS). Note that LIS-II is a generalized Gaussian elimination (GGE) procedure solving system of linear inequalities. LIS-II is capable of determining the feasible interval of individual variable as a linear inequalities feasibility analyzer (LIFA). LIS-I is a set of three key algorithms that recursively reduce maximum infeasibility, sum of all infeasibility, and the number of constraints with the worst case infeasibility for any given linear system in feasibility form. US_LS has many advantages over existing interior point methods or the ellipsoid method as US_LS is symmetric and numerical stable for all the vectors are normalized to be unit vectors on the surface of a unit shell. It is a global, symmetric, stable, and one pass approach without the need of iterative application of some key algorithms.
. Such analysis shows that it is possible to solve LIS (linear inequalities system) with non-iterative and non-Gaussian alike algorithms. The author is putting this draft together to highlight this unit shell approach. This approach is coined as LIS-III or Unit Shell for Linear Systems or (US_LS). Note that LIS-II is a generalized Gaussian elimination (GGE) procedure solving system of linear inequalities. LIS-II is capable of determining the feasible interval of individual variable as a linear inequalities feasibility analyzer (LIFA). LIS-I is a set of three key algorithms that recursively reduce maximum infeasibility, sum of all infeasibility, and the number of constraints with the worst case infeasibility for any given linear system in feasibility form. US_LS has many advantages over existing interior point methods or the ellipsoid method as US_LS is symmetric and numerical stable for all the vectors are normalized to be unit vectors on the surface of a unit shell. It is a global, symmetric, stable, and one pass approach without the need of iterative application of some key algorithms.2. Highlights
- 1. Any linear systems in feasibility form (LSF) [ref. 17]:
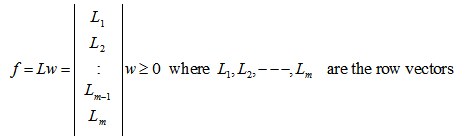 2. Linear Systems on the Unit Shell after normalization:
2. Linear Systems on the Unit Shell after normalization: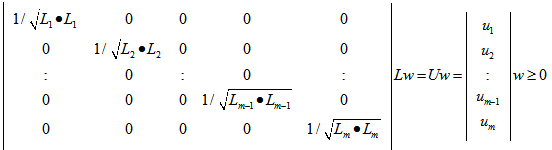 Note that each row,
Note that each row,  in U is a point on the surface of an n-dimensional unit sphere (with a radius of 1.0), namely the unit shell. The solution normalized solution,
in U is a point on the surface of an n-dimensional unit sphere (with a radius of 1.0), namely the unit shell. The solution normalized solution,  is also a point on the same unit shell. Moreover, the maximum arc distance from this point to all the points in U is minimized by the definition of a minimum cover on the unit shell for all points in U.3. A great circle arc connecting two points on a unit shellLet p and q are two points on the surface of an n-dimensional unit shell, then
is also a point on the same unit shell. Moreover, the maximum arc distance from this point to all the points in U is minimized by the definition of a minimum cover on the unit shell for all points in U.3. A great circle arc connecting two points on a unit shellLet p and q are two points on the surface of an n-dimensional unit shell, then 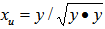 with
with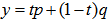 with
with 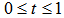 is a path on the unit shell connecting points
is a path on the unit shell connecting points 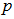 and
and 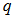 as part of the great circle that passing both points
as part of the great circle that passing both points 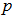 and
and 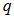 . In other words, we have the equation for all the points on the great circle arc connecting p and q:
. In other words, we have the equation for all the points on the great circle arc connecting p and q: 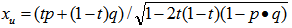 Note that
Note that 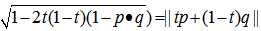 is simply the normalization factor to project the vector
is simply the normalization factor to project the vector  onto the unit shell, Consequently, the mid-point of
onto the unit shell, Consequently, the mid-point of  is
is 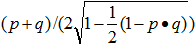 it is also the geometrical center of
it is also the geometrical center of 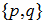 on the unit shell.4. Equidistant Point (EDP) point of a set of points,
on the unit shell.4. Equidistant Point (EDP) point of a set of points, 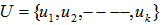 on the surface of the unit shell is any point, p, on the unit shell such that
on the surface of the unit shell is any point, p, on the unit shell such that 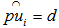 for all i.5. A Cover and the Geometrical Center of points on the unit shellThe disc centered at e with a radius of R is a cover for all the points with
for all i.5. A Cover and the Geometrical Center of points on the unit shellThe disc centered at e with a radius of R is a cover for all the points with 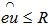 i.e.,
i.e., 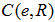 or simply
or simply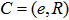 .Given a set of points,
.Given a set of points, 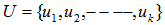 on the surface of the unit shell, a point, c, is a geometric center, GC, of
on the surface of the unit shell, a point, c, is a geometric center, GC, of 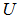 if the maximum arc distance from c to all the points in
if the maximum arc distance from c to all the points in 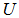 is minimized. In other words,
is minimized. In other words,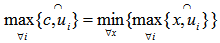 Given a set of points,
Given a set of points, 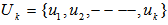 on the surface of the unit shell, let rank
on the surface of the unit shell, let rank 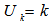 Let
Let 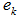 be an EDP for
be an EDP for 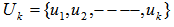 on the surface of the unit shell, let
on the surface of the unit shell, let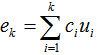 . We have
. We have 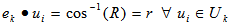 by definition of EDP; we also have
by definition of EDP; we also have 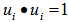 for all iHence, we should have the solution for the coefficients
for all iHence, we should have the solution for the coefficients 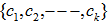 from
from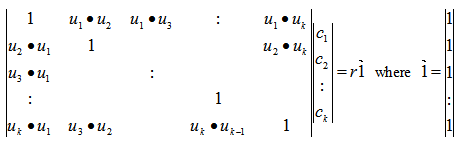 If
If 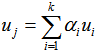 , from
, from 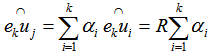 then
then 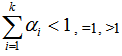 if
if 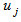 is an interior, boundary, or exterior point of the cover,
is an interior, boundary, or exterior point of the cover, 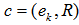 .Swapping
.Swapping 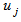 with
with 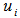 we have
we have 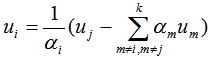 .Note: let
.Note: let 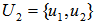 and
and 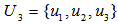 , if is outside the minimum disc cover of
, if is outside the minimum disc cover of 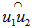 , the cover as a disc centered at an EDP,
, the cover as a disc centered at an EDP, 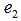 of
of 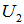 (as the geometrical center
(as the geometrical center 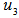 of
of 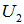 , namely,
, namely, 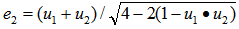 with a radius
with a radius 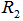 as
as 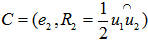 does not cover
does not cover 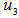 , it may still be possible to find a disc cover
, it may still be possible to find a disc cover 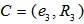 centered at
centered at 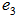 with a radius
with a radius 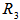 as an EDP for
as an EDP for 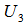 .If rank
.If rank 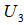 = 3, then the normalized orthogonal projection of
= 3, then the normalized orthogonal projection of 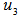 onto
onto 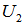 ,i.e.,
,i.e.,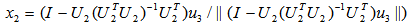 is an EDP (
is an EDP (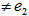 ) of
) of 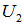 with radius
with radius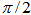 .The great circle that goes thru both
.The great circle that goes thru both 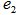 and
and 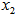 are all EDPs of
are all EDPs of 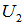 . Note that an EDP,
. Note that an EDP, 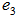 for
for 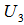 is the normalized
is the normalized 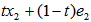 such that
such that 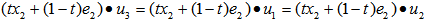 .By induction, the same argument shows that exterior points of a disc cover on the unit shell may be covered by another disc as a boundary or interior point of another EDP at a higher rank. The minimum cover is one centered at an EDP with least number of boundary points and hence, smallest radius with the smallest rank. In summary, by moving to a higher rank, one can increase the number of boundary points centered at distinct EDP or EDPs with a larger radius. How to find a second EDP with increased rank (outside the subspace on the unit shell)?Two methods are investigated:(a) Using Liner Subspace Projection Operation,
.By induction, the same argument shows that exterior points of a disc cover on the unit shell may be covered by another disc as a boundary or interior point of another EDP at a higher rank. The minimum cover is one centered at an EDP with least number of boundary points and hence, smallest radius with the smallest rank. In summary, by moving to a higher rank, one can increase the number of boundary points centered at distinct EDP or EDPs with a larger radius. How to find a second EDP with increased rank (outside the subspace on the unit shell)?Two methods are investigated:(a) Using Liner Subspace Projection Operation, 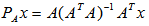 as described above.(b) Using natural basis and subspace ranking(a): Assume that we have set of unit vectors
as described above.(b) Using natural basis and subspace ranking(a): Assume that we have set of unit vectors 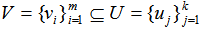 with
with 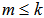 , and another unit vector,
, and another unit vector, 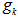 , that is an EDP for
, that is an EDP for 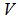 . The following steps are needed to locate another
. The following steps are needed to locate another 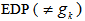 for
for 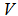 .1. Compute the maximum arc distance from
.1. Compute the maximum arc distance from  to any point in
to any point in 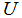 as
as 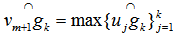 with
with 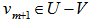 .2. Compute subspace projection of
.2. Compute subspace projection of 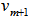 onto
onto 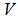 as
as 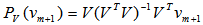 3. Identify the orthogonal component of
3. Identify the orthogonal component of 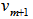 to
to 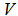 as
as 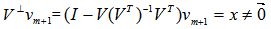 4. Normalize x to become an unit vector as
4. Normalize x to become an unit vector as 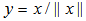 5. Move point
5. Move point 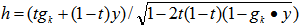 for any
for any 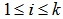 along the great circle on the unit shell towards from y towards
along the great circle on the unit shell towards from y towards 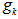 such that
such that 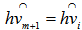 , i.e., we have
, i.e., we have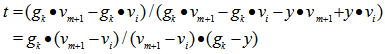 for
for 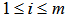 Alternative, for
Alternative, for 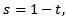
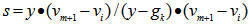 for
for 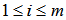 (b): Hint:Let
(b): Hint:Let 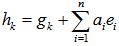 , where
, where 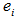 is the unit vector with 1 at its i-th position and 0 otherwise. Note that in the above equality,
is the unit vector with 1 at its i-th position and 0 otherwise. Note that in the above equality, 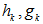 and
and 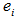 are n-dimensional vectors while
are n-dimensional vectors while 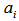 is a scalar real number, in other words,We have,
is a scalar real number, in other words,We have, 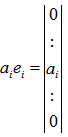 Solve
Solve 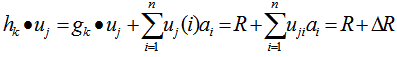 for
for 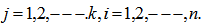 dimensional vector with its i-th component,
dimensional vector with its i-th component, 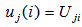 Namely, we treat
Namely, we treat 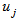 as a row vector
as a row vector 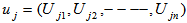 .Note that
.Note that 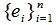 has full rank n
has full rank n 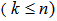 , if k<n, we can find at least one
, if k<n, we can find at least one 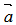
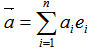 from
from 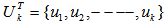 , such that we have
, such that we have 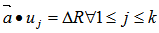 For
For 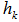 to be an EDP distinct from
to be an EDP distinct from 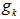 for
for 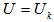 , we must have
, we must have 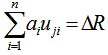 for j=1,2,…..,k. Namely,
for j=1,2,…..,k. Namely, 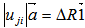 , i.e.,
, i.e.,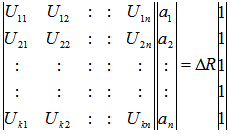 In other words, any unit vector as normalized
In other words, any unit vector as normalized 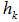 with
with 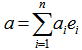 obtained from
obtained from 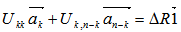 is an EDP
is an EDP 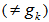 for
for 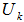 6. Four cases of relationship of
6. Four cases of relationship of 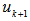 with
with 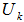 .CASE I. Rank
.CASE I. Rank 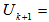 Rank
Rank 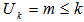 and minimum
and minimum 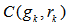 covers
covers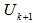 .
. we have
we have 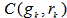 also a minimum cover of
also a minimum cover of  .CASE II. Rank
.CASE II. Rank  Rank
Rank 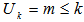 and minimum
and minimum 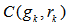 does not cover
does not cover 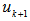 .CASE III. Rank
.CASE III. Rank 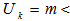 Rank
Rank 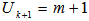 and minimum
and minimum 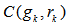 covers
covers 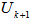 .
.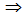 It is possible to locate another EDP,
It is possible to locate another EDP, 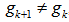 , for
, for 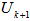 such that
such that 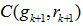 covers
covers 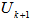 with
with 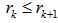 .
. 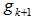 is obtained from the great circle arc connecting
is obtained from the great circle arc connecting 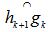 where
where 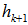 is the normalized
is the normalized 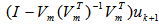 for any full ranked
for any full ranked 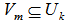 .CASE VI. Rank
.CASE VI. Rank 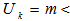 Rank
Rank 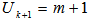 and minimum
and minimum 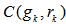 does not cover
does not cover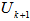 .Analysis: For CASE II,Let
.Analysis: For CASE II,Let 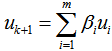 , we have
, we have 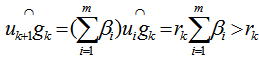 ; hence
; hence 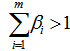 .Move a point
.Move a point 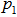 , from
, from 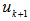 towards
towards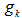 along the great circle arc
along the great circle arc 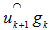 , until we have
, until we have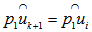 for at least one
for at least one 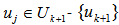 . Let
. Let 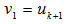 and
and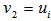 ,Let
,Let 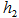 as the midpoint of
as the midpoint of 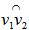 , select
, select 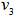 from
from 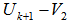 such that
such that 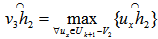 .For i=2,3 ----, m we can select linearly independent subset
.For i=2,3 ----, m we can select linearly independent subset 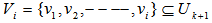 Such that we can find at least one
Such that we can find at least one 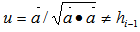 such that
such that 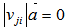 , i.e.,
, i.e., Let
Let 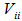 be any full ranked I by I sub-matrix of
be any full ranked I by I sub-matrix of 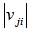 , we have
, we have 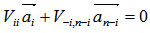 Solve for
Solve for 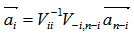 Normalized
Normalized 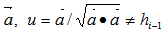 is an EDP of
is an EDP of 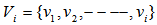 and the great circle arc
and the great circle arc 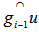 connecting
connecting 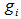 and
and 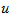 are all EDP for
are all EDP for 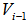 .
.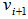 is selected from
is selected from 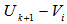 such that
such that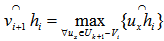 . When
. When 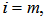 we have a new cover
we have a new cover 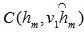 for
for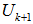 . For CASE IV, It is possible to locate another EDP
. For CASE IV, It is possible to locate another EDP 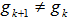 for
for 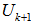 such that a hemispherical cover for
such that a hemispherical cover for 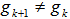 is obtained. This is because
is obtained. This is because 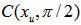 is a hemispherical cover of
is a hemispherical cover of 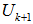 where
where 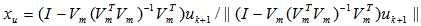 .7. Arc connecting two EPDs on Unit ShellIf points p and q are distinct equidistant points (EDP) for
.7. Arc connecting two EPDs on Unit ShellIf points p and q are distinct equidistant points (EDP) for 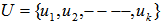 on the surface of the unit shell, then, all the points on the great circle connecting p and q are all EDPs for
on the surface of the unit shell, then, all the points on the great circle connecting p and q are all EDPs for 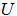 .Proof:Let p and q be two distinct equidistant points for
.Proof:Let p and q be two distinct equidistant points for 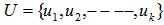 , we have
, we have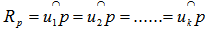 and
and 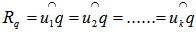 .Let
.Let 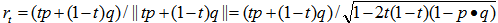 be a normalized unit vector on the great circle connecting p and q. Then, it is clear that we have
be a normalized unit vector on the great circle connecting p and q. Then, it is clear that we have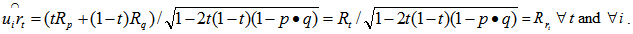 Where
Where 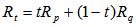 and
and 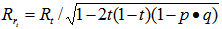 .8. The US-LS algorithm, a unit shell algorithm to minimize the maximum infeasibility of a linear system in feasibility form, Excel is used to carry out this proposed algorithm step by step to solve a simple LP in LSF form with 7 variables and 14 constraints:Step 1. Problem formulation: Let the LSF be normalized such that every row vector is an unit vector with it end point on the unit shell, we have the normalized solution of the LP also an unit vector on the unit shell and the problem becomes given an matrix with k unit vectors as
.8. The US-LS algorithm, a unit shell algorithm to minimize the maximum infeasibility of a linear system in feasibility form, Excel is used to carry out this proposed algorithm step by step to solve a simple LP in LSF form with 7 variables and 14 constraints:Step 1. Problem formulation: Let the LSF be normalized such that every row vector is an unit vector with it end point on the unit shell, we have the normalized solution of the LP also an unit vector on the unit shell and the problem becomes given an matrix with k unit vectors as 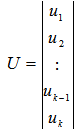 , locate a unit vector,
, locate a unit vector, 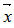 such that we have
such that we have 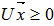 .Step 2. Select a pair of distinct points,
.Step 2. Select a pair of distinct points, 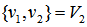 from rows in
from rows in 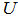 such that
such that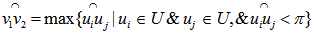 compute the midpoint,
compute the midpoint, 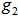 , of
, of 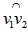 as it is described in section 3.0. Note that
as it is described in section 3.0. Note that 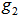 is both an EDP (equal distanced point) and the geometrical center of
is both an EDP (equal distanced point) and the geometrical center of 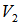 .Step 3. Compute the subspace projection of
.Step 3. Compute the subspace projection of  as
as 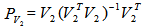 .Step 4. Find the first unit vector,
.Step 4. Find the first unit vector, 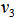 from the unit vectors of
from the unit vectors of 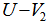 such that the arc distance
such that the arc distance 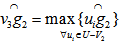 and that the normalized
and that the normalized 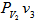 is not equal to
is not equal to 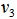 . In other words, let
. In other words, let 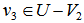 such that
such that 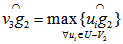 and
and 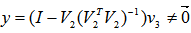 . Note that we have rank
. Note that we have rank 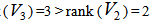 where
where 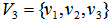 Step 5. Normalize vector
Step 5. Normalize vector 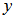 to become an unit vector
to become an unit vector 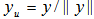 , then
, then 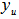 is also an unit vector with its end point on the surface of the unit shell. Note that both
is also an unit vector with its end point on the surface of the unit shell. Note that both 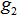 and
and 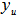 are EDPs for points in
are EDPs for points in 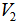 . Consequently, the great circle
. Consequently, the great circle 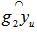 are all EDP for
are all EDP for 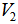 . On this great circle, one can locate a unique point,
. On this great circle, one can locate a unique point, 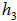 as the shortest EPD for
as the shortest EPD for 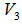 by the following two equations:a.
by the following two equations:a. 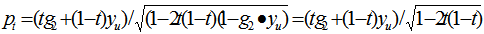 as
as 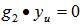
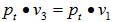 (note that we will always have
(note that we will always have 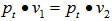 b. as
b. as 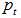 is also an EDP for
is also an EDP for 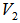 .Solve for t, from a. and b., we have, note that we have
.Solve for t, from a. and b., we have, note that we have 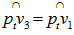 , hence,
, hence, 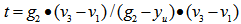 .Substitute
.Substitute 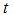 into equation a., we have the shortest EDP or the geometrical center,
into equation a., we have the shortest EDP or the geometrical center, 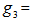
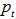 for
for 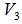 .Steps 2 to 5 can be repeated with increasing subscription for
.Steps 2 to 5 can be repeated with increasing subscription for 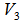 and
and 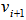 for
for 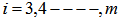 where m=rank (U).Step 6. Once the highest rank for, m, for
where m=rank (U).Step 6. Once the highest rank for, m, for 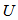 has reached, we have a geometrical center,
has reached, we have a geometrical center, 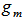 of
of 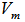 such that
such that 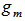 is an EDP for
is an EDP for 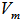 . For all rows (points) of
. For all rows (points) of 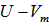 , compute
, compute 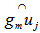 for maximum arc distance
for maximum arc distance 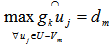 . If
. If 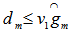 , then we have identified a minimum cover
, then we have identified a minimum cover 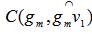 .If
.If 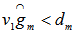 , we have
, we have 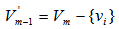 has rank m-1, the orthogonal projection
has rank m-1, the orthogonal projection 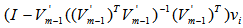 normalized is an EDP
normalized is an EDP 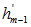 for
for 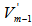 and has its arc distance to all points in
and has its arc distance to all points in 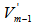 as
as 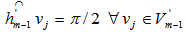 . In other words, we have
. In other words, we have 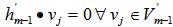 . If a hemispherical cover,
. If a hemispherical cover, 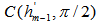 for
for 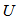 exists, it must be one of these m possible
exists, it must be one of these m possible 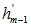 .9. An Example: Consider the following sample LP pairs as primal and its dual [Refs 1 to 7].
.9. An Example: Consider the following sample LP pairs as primal and its dual [Refs 1 to 7].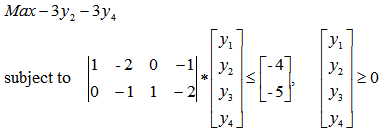
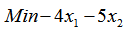
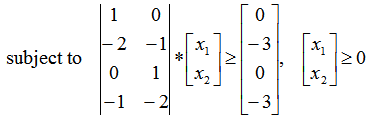 In self-dual formulation as pure linear inequalities, we have:
In self-dual formulation as pure linear inequalities, we have: Normalize (1) to have all row vectors as points,
Normalize (1) to have all row vectors as points, 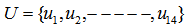 on the 7-dimensional unit shell, we have
on the 7-dimensional unit shell, we have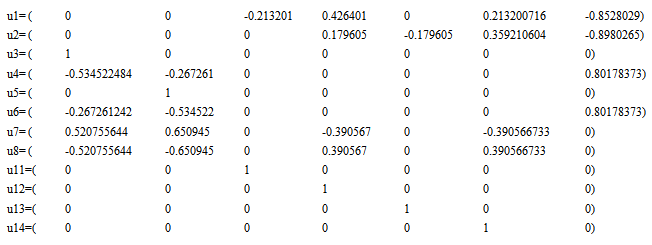 Let
Let 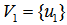 , we have
, we have 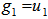 ,
, 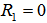 , from
, from 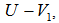 we determine
we determine 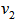 such that
such that 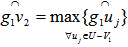 , we have
, we have 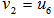 , i.e.,
, i.e.,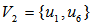 , the geometrical center of
, the geometrical center of 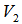 is the midpoint of
is the midpoint of 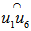 , we have
, we have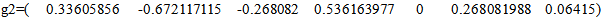 Hence,
Hence, 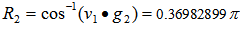 .
.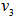 is determined from
is determined from 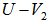 such that
such that  , we have
, we have 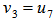 , i.e.,
, i.e.,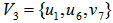 , Note that
, Note that 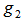 is both EDP and the geometrical center of
is both EDP and the geometrical center of 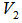 .To locate the geometrical center which is also an EDP for
.To locate the geometrical center which is also an EDP for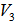 , we can compute the orthogonal projection
, we can compute the orthogonal projection 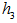 of
of 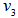 of the subspace
of the subspace 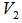 , i.e.,
, i.e., 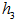 is the normalized unit vector of
is the normalized unit vector of 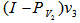 where
where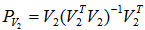 . Note that this normalized unit vector
. Note that this normalized unit vector 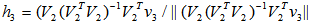 is orthogonal to points in
is orthogonal to points in  and has an arc distance of
and has an arc distance of  to all the points in
to all the points in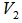 . In other words, we have identified another EDP for
. In other words, we have identified another EDP for 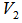 that is distinct from
that is distinct from 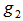 .The great circle arc
.The great circle arc 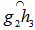 connecting
connecting 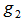 and
and 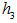 are all EDP for
are all EDP for 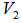 and the geometrical center for
and the geometrical center for 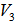 is also a point,
is also a point, 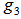 , on this great circle arc as an EDP for
, on this great circle arc as an EDP for 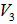 with the minimum radius. There is only one such point as the normalized
with the minimum radius. There is only one such point as the normalized 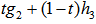 with t computed as shown in Step 5.In this example, we have:
with t computed as shown in Step 5.In this example, we have: Using Excel, we have t=0.210480823 and
Using Excel, we have t=0.210480823 and 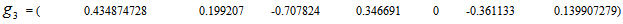 Hence, we have
Hence, we have 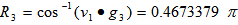 .Continue this process for
.Continue this process for 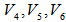 , and
, and 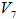 until we reach the maximum possible rank of 7 as:
until we reach the maximum possible rank of 7 as: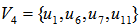 with
with 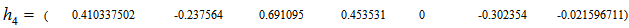 Using Excel, we have t =0.460315637 and
Using Excel, we have t =0.460315637 and 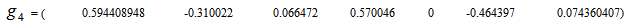 We have
We have 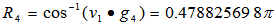
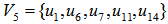 with
with  Using Excel, we have t=0.598264383 and
Using Excel, we have t=0.598264383 and 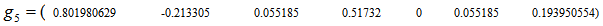 We have
We have 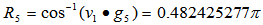
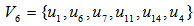 with
with  Using Excel, we have t= 0.483043855 and
Using Excel, we have t= 0.483043855 and  We have
We have 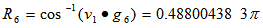 From
From 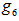 , we identified the unit vector orthogonal to
, we identified the unit vector orthogonal to 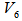 from
from 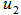 as
as 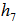
 Using Excel, we have t= 0.468058988 and
Using Excel, we have t= 0.468058988 and 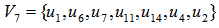 Figure 1 illustrates the arc distance of
Figure 1 illustrates the arc distance of 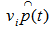 and the arc distance of
and the arc distance of 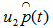 for
for 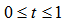 where
where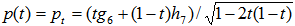 . As
. As 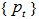 for different value of t are all EDPs for
for different value of t are all EDPs for 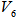 , we have an EDP for
, we have an EDP for 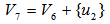 at t= 0.468058988.
at t= 0.468058988.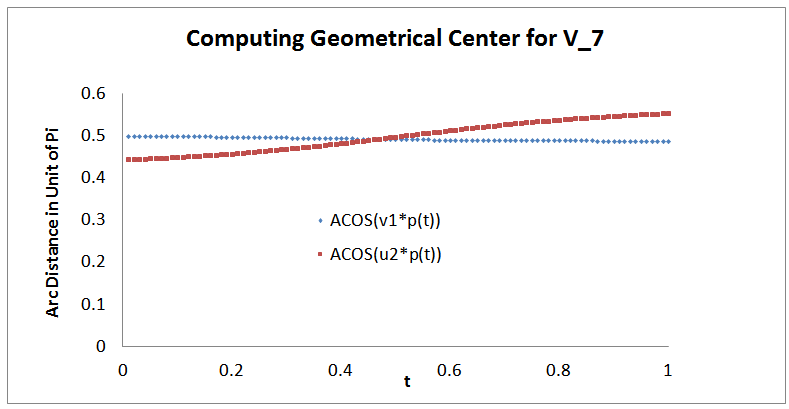 | Figure 1. Computing EDP for  as as  |
 With
With 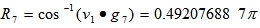 .We have reached the geometrical center as an EDP for a full ranked
.We have reached the geometrical center as an EDP for a full ranked 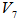 as
as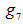 . The only possible hemispherical cover for
. The only possible hemispherical cover for 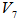 is centered at the normalized
is centered at the normalized 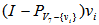 and
and 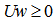 has solution if and only if such as hemispherical cover for
has solution if and only if such as hemispherical cover for 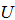 exists.It is trivial to check that the unit vector
exists.It is trivial to check that the unit vector 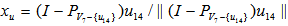 is the solution of
is the solution of 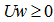 for the original LP. In other words, we have identified the hemispherical cover
for the original LP. In other words, we have identified the hemispherical cover 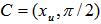 for all the 14 points in
for all the 14 points in  with
with 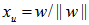 .With Excel, we have:
.With Excel, we have: To verify that
To verify that 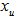 is indeed the solution of the original LP in (1), we have
is indeed the solution of the original LP in (1), we have 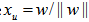 such that
such that 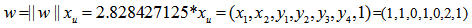 Hence the solution to the LP in (1) is:
Hence the solution to the LP in (1) is: 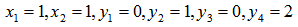
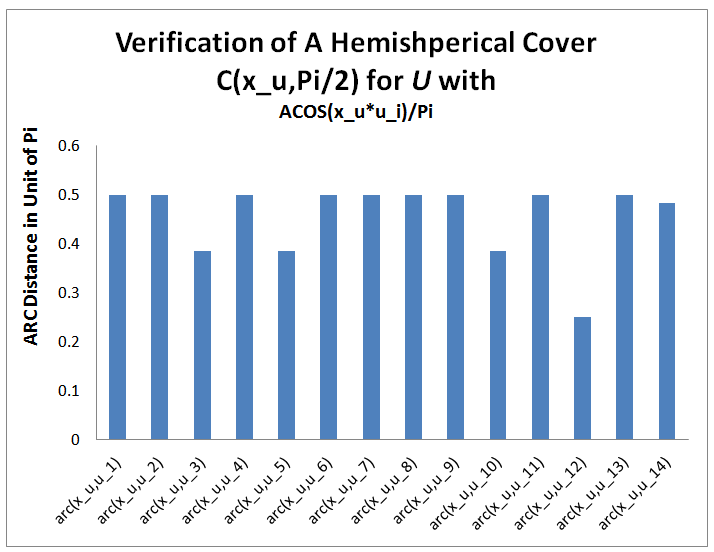 | Figure 2. Solution of LP as the Center of a Hemispherical Cover, 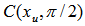 for for 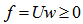 |
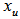 , such an EDP for
, such an EDP for  as the geometrical center of
as the geometrical center of 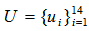 . Note that such a solution point is a point with a minimum arc distance to all the constraint points. In other words, it has the minimum arc distance to all the constraint points. It is the best solution to any given set of linear inequalities that can be humanly resolved. The solution obtained from the unit shell is identical to that obtained by either the simplex method, interior point method, LIS-I, or the GGE (LIS-II) approaches. Over the past few years, the author has developed three different methods for solving any linear systems and they are as efficient as the text book simplex and interior point methods with considerable simplification and numerical stability.This paper details the theory and steps of such a generic algorithm to solve both linear equalities and inequalities on the Unit Shell with a minimum number of steps involving only the unit vectors and linear subspace projection operation
. Note that such a solution point is a point with a minimum arc distance to all the constraint points. In other words, it has the minimum arc distance to all the constraint points. It is the best solution to any given set of linear inequalities that can be humanly resolved. The solution obtained from the unit shell is identical to that obtained by either the simplex method, interior point method, LIS-I, or the GGE (LIS-II) approaches. Over the past few years, the author has developed three different methods for solving any linear systems and they are as efficient as the text book simplex and interior point methods with considerable simplification and numerical stability.This paper details the theory and steps of such a generic algorithm to solve both linear equalities and inequalities on the Unit Shell with a minimum number of steps involving only the unit vectors and linear subspace projection operation 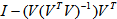 . A simple LP solved with this new technique is demonstrated step by step with Excel tabulation and matrix operations. The support is attached for verification and validation of this new approach.10. Solving Differential Variation Inequalities (DVI) on the Unit-Shell We generalize the unit-shell algorithm over linear space to a normed Banach space with an inner-product operator
. A simple LP solved with this new technique is demonstrated step by step with Excel tabulation and matrix operations. The support is attached for verification and validation of this new approach.10. Solving Differential Variation Inequalities (DVI) on the Unit-Shell We generalize the unit-shell algorithm over linear space to a normed Banach space with an inner-product operator 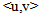 with norm
with norm 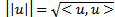 for solving variational inequalities (VI) or differential variational inequalities (DVI) as follows [refs 14 and 15]:Let
for solving variational inequalities (VI) or differential variational inequalities (DVI) as follows [refs 14 and 15]:Let 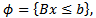 where B is an
where B is an 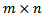 matrix as a nonempty convex compact polyhedron in
matrix as a nonempty convex compact polyhedron in 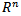 Let
Let 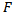 be a continuously differentiable function from
be a continuously differentiable function from 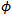 into
into 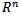 with Jacobian
with Jacobian 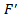 .The variational inequality problem (VIP) associated with
.The variational inequality problem (VIP) associated with 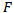 and
and 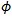 is to locate a solution
is to locate a solution 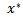 in
in 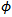 satisfying the variational inequality (VI):
satisfying the variational inequality (VI): 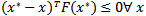 in
in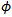 . Note that in
. Note that in 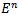 , we have
, we have 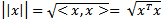 Let the gap function associated with a VIP be defined for
Let the gap function associated with a VIP be defined for 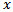 in
in 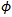 as:
as: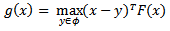 While the dual gap function associated with a VIP is defined as
While the dual gap function associated with a VIP is defined as 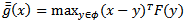 Using Newton’s first order Taylor linear approximation around a point
Using Newton’s first order Taylor linear approximation around a point 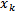 in
in 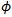 , a linearized VIP as LVIP can be computed iteratively for
, a linearized VIP as LVIP can be computed iteratively for 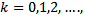 as:
as: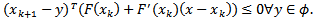 Consider the following nonconvex, nonlinear constrained mathematical program:
Consider the following nonconvex, nonlinear constrained mathematical program: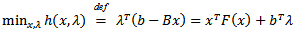 subject to
subject to 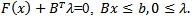 Note that optimality occurs at:
Note that optimality occurs at: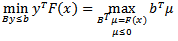 subject to:
subject to: 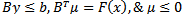 Consequently, we have the following homogeneous linear feasible system of inequalities
Consequently, we have the following homogeneous linear feasible system of inequalities 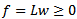
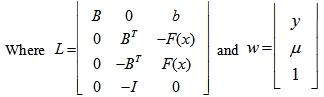 Note that
Note that 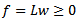 can be solved effectively over the unit shell using only linear projection and the concept of equi-distanced points to selected set of normalized unit vectors derived from row vectors of L as described and demonstrated in this draft paper from Section 1.0 to Section 8.0.11. Other Examples of Linear Programs Solved by the Unit Shell ApproachFirst, Any non-homogeneous linear system with equalities, inequalities, or mixed as constraints may be converted to homogeneous linear system by increased its number of columns as variables by 1 shifting the right hand side vector to the left hand side so that the right hand side is always a vector with only zero coefficients. The row vectors of such a homogeneous linear system can always be normalized into vector of unit length as unit vector on the surface of a n-dimensional unit sphere as the unit shell. The normalized solution of such a homogeneous linear system is also a unit vector on the same unit-shell. In this section, the author provides both theoretical analysis and examples for four possible cases of solving homogeneous linear systems on the unit shell, namely, with unique solution, no solution, infinite solutions, and solutions that are unbounded. Both unbounded and infeasible LPs are examined and analyzed to provide necessary and sufficient conditions for linear systems with null or infinite many solutions such that the solvability of any system of linear equalities or inequalities are resolved with a computational complexity that is compatible to that of the traditional Gaussian Elimination for system of linear equalities, namely,
can be solved effectively over the unit shell using only linear projection and the concept of equi-distanced points to selected set of normalized unit vectors derived from row vectors of L as described and demonstrated in this draft paper from Section 1.0 to Section 8.0.11. Other Examples of Linear Programs Solved by the Unit Shell ApproachFirst, Any non-homogeneous linear system with equalities, inequalities, or mixed as constraints may be converted to homogeneous linear system by increased its number of columns as variables by 1 shifting the right hand side vector to the left hand side so that the right hand side is always a vector with only zero coefficients. The row vectors of such a homogeneous linear system can always be normalized into vector of unit length as unit vector on the surface of a n-dimensional unit sphere as the unit shell. The normalized solution of such a homogeneous linear system is also a unit vector on the same unit-shell. In this section, the author provides both theoretical analysis and examples for four possible cases of solving homogeneous linear systems on the unit shell, namely, with unique solution, no solution, infinite solutions, and solutions that are unbounded. Both unbounded and infeasible LPs are examined and analyzed to provide necessary and sufficient conditions for linear systems with null or infinite many solutions such that the solvability of any system of linear equalities or inequalities are resolved with a computational complexity that is compatible to that of the traditional Gaussian Elimination for system of linear equalities, namely, 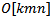 where k is the rank of the linear system (equalities and inequalities included) with m constraints and n variables.11.1. Necessary, Sufficient Conditions, and Examples for the Four Cases of Linear Systems with Unique Solution, No Solution, Infinite Many Solution, and Unbounded Linear SolutionExample in Section 8 clearly illustrated the fact that when the rank of the homogenous linear inequalities equals to the number of unknowns plus 1, and all the unit vectors associated with the homogenous linear inequalities are reachable (or covered) by the hemispherical cover of the unit shell centered at:
where k is the rank of the linear system (equalities and inequalities included) with m constraints and n variables.11.1. Necessary, Sufficient Conditions, and Examples for the Four Cases of Linear Systems with Unique Solution, No Solution, Infinite Many Solution, and Unbounded Linear SolutionExample in Section 8 clearly illustrated the fact that when the rank of the homogenous linear inequalities equals to the number of unknowns plus 1, and all the unit vectors associated with the homogenous linear inequalities are reachable (or covered) by the hemispherical cover of the unit shell centered at: 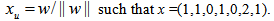 If all the unit vectors associated with a given homogenous linear system can not be covered by such a hemispherical cover, it does not have a solution and the conflicting inequalities can be easily identified. On the other hand, if the rank of hemispherical cover is less than the number of unknowns, we will have an infinite number of EDPs for all the constraint inequalities, hence, it will have infinite many solutions or as unbounded cases.
If all the unit vectors associated with a given homogenous linear system can not be covered by such a hemispherical cover, it does not have a solution and the conflicting inequalities can be easily identified. On the other hand, if the rank of hemispherical cover is less than the number of unknowns, we will have an infinite number of EDPs for all the constraint inequalities, hence, it will have infinite many solutions or as unbounded cases.3. Conclusions and Future Work
- In conclusion, the author presents an innovative approach that relates algebraic relation in vectors to geometrical relation as arc distance on the unit shell, i.e., the surface of a n-dimensional hyper sphere.The solution or solutions to any given linear system (both equalities and inequalities included) is shown to be the geometrical center or centers that are points on the unit shell with its maximum arc distance to all the constraints point minimized. This technique is illustrated and verified with an example of solving a linear program (LP) with 7 variables and 14 constraints. Only the dot product and linear subspace projection operation are used to locate the geometrical center or centers with a minimum number of steps. As dot product of two unit vectors is a direct measurement of correlation between two sets of numbers, the geometrical center or centers do reveal maximum correlation with minimum discrepancy. When we can compute efficiently the geometrical centers of a set of constraint points, it is applicable to a very wide range of scientific and engineering applications in aviation, finance, economics, operations research (OR), data mining, signal processing, and pattern recognition … etc. Additional benefit of dealing with only unit vectors is its numerical stability free from ill-conditioned operations that other approaches encountered very frequently. A future plan is to implement the unit shell algorithm in java as a generic optimization tool for general purpose scientific and engineering use.In addition, the author is working on recursive projection and distance functions for unit vectors onto its k-dimensional subspaces and its direct application in solving homogeneous linear inequalities. This approach does provide effective and numerical stable algorithms that can handle very large system of linear inequalities with a computational complexity compatible to the classic Gaussian for solving system of linear equalities. This approach is extremely handy in dealing with linear inequalities with millions of unknowns and/or constraints. A drafted paper is currently under peer review by both mathematician and engineers. Figure 3 illustrates the possibility of using recursively projection and distance functions in trigonometry as Sin and Cos functions to replace the classic linear space projector,
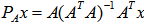 , and its orthogonal operators:
, and its orthogonal operators: 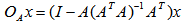 .In Figure 3,
.In Figure 3, 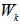 is a linear subspace with dimension and rank = k and an orthogonal basis.Note that the computational complexity of locating such a geometry center for the set of normalized homogenous linear inequalities can be shown to be compatible to that of the classic Gaussian Elimination solving systems of linear equalities.Support from NSF funding or private foundations source in innovative mathematical computation for further clarification and elaboration will be pursued.
is a linear subspace with dimension and rank = k and an orthogonal basis.Note that the computational complexity of locating such a geometry center for the set of normalized homogenous linear inequalities can be shown to be compatible to that of the classic Gaussian Elimination solving systems of linear equalities.Support from NSF funding or private foundations source in innovative mathematical computation for further clarification and elaboration will be pursued.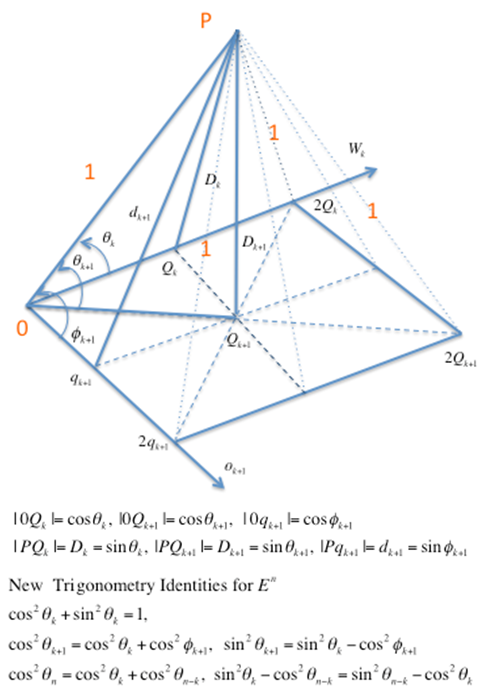 | Figure 3. Recursive Linear Subspace Projection and Distance Functions as Trigonometry Identities |
ACKNOWLEDGEMENTS
- The author acknowledges valuable suggestions, comments, and initial peer review of the concept of the Unit Shell by his colleagues, in particular, David Hammrick, Dr. Leone C. Monticone, and Dr. William P. Niedringhaus during past 10 years at the MITRE Corporation. Latest discussion and comments from Oliver C. Wang and Brian M. Jones have contributed to the clarity of the role of linear projection and orthogonal distance functions relevant to solving linear inequalities. Peer reviews and editorial enhancements from the referees and editors at Scientific & Academic Publishing (SAP), USA is also essential for the correctness and readability of this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML