Ranjita Pandey
Department of Statistics, University of Delhi, 110007, Delhi
Correspondence to: Ranjita Pandey, Department of Statistics, University of Delhi, 110007, Delhi.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, the problem of shrinkage estimation of reliability function is considered from a type II censored sample, assuming availability of prior estimate of reliability function. We develop four empirical shrinkage estimators for the reliability function pertaining to a class of lifetime distributions comprising of five distinct failure time distributions commonly used for modelling life-data in the industry. The proposed estimators are compared with Maximum Likelihood Estimators (MLEs) in terms of the mean squared error (MSE). All the proposed empirical shrinkage estimators are shown to be preferable to MLEs as the shrunken estimators remain more efficient in comparison. As the prior value of the reliability function approaches closer to the true value of the reliability function, the efficiency of the proposed estimators improves, for all the truncation numbers.
Keywords:
Family of Lifetime Distributions, Type II Censoring, Shrinkage Estimation, Reliability Function
Cite this paper: Ranjita Pandey, Shrinkage Estimation of Reliability Function for Some Lifetime Distributions, American Journal of Computational and Applied Mathematics , Vol. 4 No. 3, 2014, pp. 92-96. doi: 10.5923/j.ajcam.20140403.04.
1. Introduction
Shrinkage estimators were introduced in literature by Thompson (1968). Inferential estimation is often undertaken in the backdrop of prior knowledge in the form of existing data, which a researcher may utilize in order to get a more precise and accurate estimate. In many situations, the experimenter has some prior information regarding parameters in the form of a point guess value. To utilize this guess value the shrinkage estimators for mean, shape and scale parameters of various lifetime distributions have been discussed by a number of authors under Bayesian and non-Bayesian set up. See, for instance, Pandey (1983), Casella and Lehmann (1988), Prakash and Singh (2006, 2008, 2009), Singh et al. (2000). However, shrinkage estimation of reliability function for any of the known lifetime distributions except exponential distribution (Tse and Tso (1996) and Chiou (1993)) has not been addressed so far, in the authors' knowledge. The advantages of incorporating prior information in the reliability function through the shrinkage estimators has been studied by Baklizi (2003). The current work is an effort to coin unified shrinkage estimators of reliability function for five lifetime distributions commonly used to model lifetime data by biologists, physicists, engineers and statisticians for living and non-living entities. Chaturvedi and Singh (2006) have derived a family of lifetime distributions which comprise of these five important lifetime distributions, namely, exponential, Weibull, Burr, Pareto and Rayleigh distributions. They have studied behavior of the hazard-rate for different members of this family. The present paper proposes four different versions of shrinkage estimators for the reliability function of a family of lifetime distributions when the data is type II censored and a prior estimate of the reliability is given. The present work is an effort to provide a single efficient reliability estimator for the five most commonly used lifetime distributions in Industry, under different censoring scenarios, for Type II censored data. The estimators suggested in the present paper are based on MLE, UMVUE and the P-values. These estimators perform better than the more popular Maximum Likelihood Estimates (MLEs) used in distribution theory, see for instance, Zacks and Even (1996). The Shrinkage estimators are developed in section 2. Numerical computations are carried out to investigate the behavior of these estimators under section 3. Results are discussed in the final section.
2. Shrinkage Estimation
Random variable X follows the family of lifetime distributions with parameters β and θ . The probability density function of X is given by | (1) |
Let g(x), 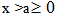 be real-valued, differentiable, strictly increasing function of x (increasing to infinity) with g(a)=0 and g’(x) stands for the derivative of g(x). We assume that the inverse function g-1 (x) of g(x) exists. The following are special cases:(i) For g(x) = x, β = 1, we obtain exponential distribution.(ii) For g(x) = x, we obtain Weibull distribution.(iii) For g(x) = log(1+xb), b>0 and β = 1,we obtain Burr distribution.(iv) For g(x) = log(x/a) and β = 1, we obtain Pareto distribution.(v) For g(x) = x, β = 2, we obtain Rayleigh distribution.The quantity we want to estimate is
be real-valued, differentiable, strictly increasing function of x (increasing to infinity) with g(a)=0 and g’(x) stands for the derivative of g(x). We assume that the inverse function g-1 (x) of g(x) exists. The following are special cases:(i) For g(x) = x, β = 1, we obtain exponential distribution.(ii) For g(x) = x, we obtain Weibull distribution.(iii) For g(x) = log(1+xb), b>0 and β = 1,we obtain Burr distribution.(iv) For g(x) = log(x/a) and β = 1, we obtain Pareto distribution.(v) For g(x) = x, β = 2, we obtain Rayleigh distribution.The quantity we want to estimate is 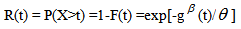 We consider a random sample of size n from this distribution such that the data is censored when a predetermined number of failures r occur: Type II censoring. In type II censoring testing is terminated at the observed time of the r th failure. The censoring time is a random variable while r is fixed.Joint pdf of
We consider a random sample of size n from this distribution such that the data is censored when a predetermined number of failures r occur: Type II censoring. In type II censoring testing is terminated at the observed time of the r th failure. The censoring time is a random variable while r is fixed.Joint pdf of  is given by
is given by Assuming β to be a known quantity, mle of
Assuming β to be a known quantity, mle of 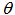 is
is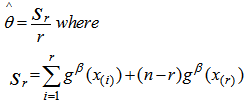 | (2) |
Baklizi (2003) has suggested shrinkage estimators of the following form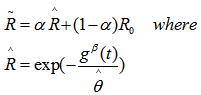 | (3) |
Such that  is estimated by mle of
is estimated by mle of  ,
,  is the prior guess of the experimenter which may be based on information based on the past experience. For a specified value of
is the prior guess of the experimenter which may be based on information based on the past experience. For a specified value of  we can calculate
we can calculate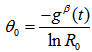 | (4) |
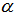 is assumed to lie between 0 and 1 inclusive, which may be determined in the following ways :
is assumed to lie between 0 and 1 inclusive, which may be determined in the following ways : is chosen such that it minimizes mean square error of
is chosen such that it minimizes mean square error of  given by
given by 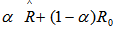 .Therefore,
.Therefore,  where
where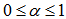 | (5) |
It is known that under Type II censoring 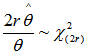 exactly. Thus, we have
exactly. Thus, we have 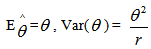 | (6) |
We postulate the following notations: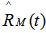 MLE of the reliability
MLE of the reliability 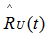 UMVUE of reliabilityWe now obtain
UMVUE of reliabilityWe now obtain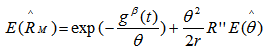
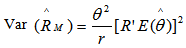
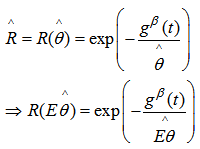
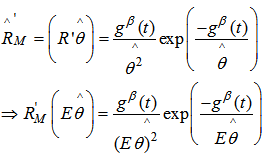
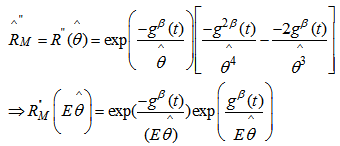
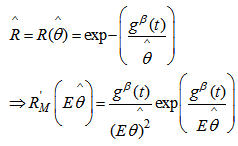
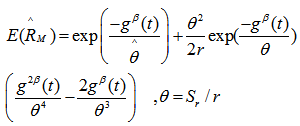 | (7) |
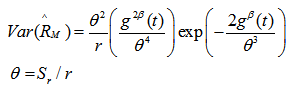 | (8) |
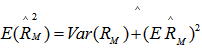 | (9) |
Next using UMVUE of reliability function,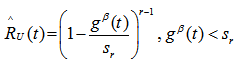 | (10) |
(Chaturvedi & Singh, 2006)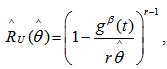 | (11) |
Using Taylor’s expansion,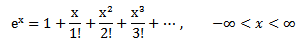
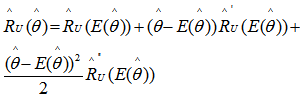 | (12) |
Therefore we can now write as under,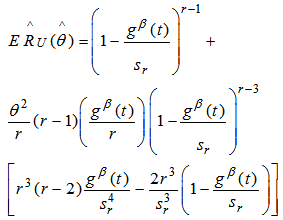 | (13) |
 | (14) |
By definition, 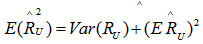 | (15) |
The first shrinkage estimator  is based on MLE which is obtained by substituting
is based on MLE which is obtained by substituting  with
with  ,
,  with
with  and
and 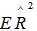 with
with 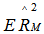 for a specified value of
for a specified value of 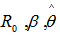 each, in expressions 2.3 and 2.5 .The second shrinkage estimator
each, in expressions 2.3 and 2.5 .The second shrinkage estimator 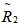 is based on UMVUE which is obtained by substituting
is based on UMVUE which is obtained by substituting  with
with  ,
, 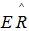 with
with 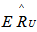 and
and  with
with 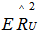 for a specified value of
for a specified value of 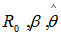 each, in expressions 2.3 and 2.5The third shrinkage estimator
each, in expressions 2.3 and 2.5The third shrinkage estimator  is based on P-value of the following test
is based on P-value of the following test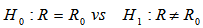
 , is assumed under H0.Let t represent the observed value of the statistic T.The P-value for this test is
, is assumed under H0.Let t represent the observed value of the statistic T.The P-value for this test is 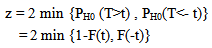 | (16) |
where F(.) is the distribution function of T.A large P-value indicates that R is close to the prior estimate R0 (Tse & Tso, 1996). The proposed shrinkage estimator is obtained by replacing 1-α with the P-value of this test.The Fourth shrinkage estimator 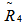 is based on the square root of the P-value of the above test such that the shrinkage estimator is obtained by replacing 1-α with the square root of the P-value of this test.
is based on the square root of the P-value of the above test such that the shrinkage estimator is obtained by replacing 1-α with the square root of the P-value of this test.
3. Relative Efficiencies of the Estimators
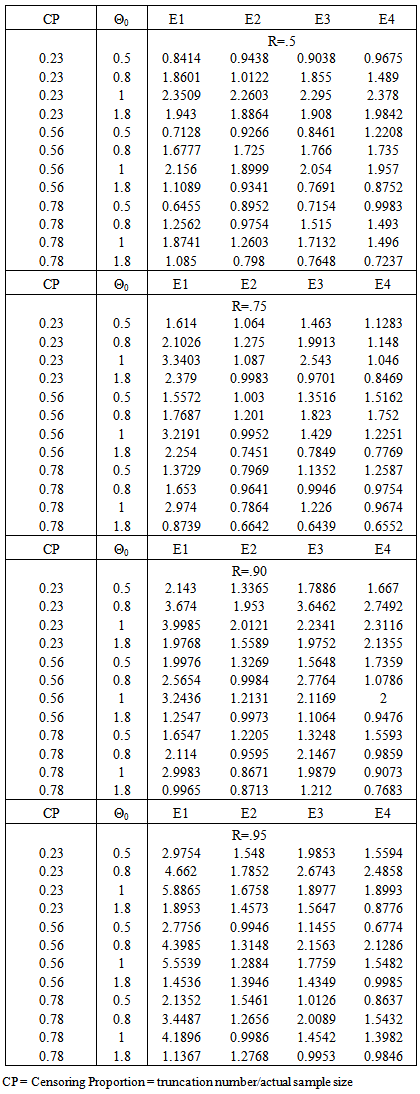
Based on the following data taken from Martz and Waller (1982, p.395), various shrinkage estimators are calculated and their performance is assessed relative to MLEs using ratios of Mean Square Errors, represented by Ei,, i=1,2,3,4.Nine failure times for a heat exchanger used in alkylation unit of a gasoline refinery were recorded as under:.41, .58, .75, .83, 1.00, 1.08, 1.17, 1.25, and 1.35 years. A Weibull distribution (g(x)=x), with paramerer β = 3.5 has been used to model this data. The family of lifetime distributions that has been considered in this paper contains Weibull distribution as a special case. Under Type II censoring, for the subsequent computations, the following are postulated:1. R: the true value of the reliability, which is taken as .5, .75 and .90.2. Θ0: taken as .5, .8, 1 and 1.8.3. Truncation number r = 2,5,7,9 have been considered.We, thus, investigate efficiency of the newly constructed shrunken estimators relative to the MLE by postulating the above permutation of scenarios for the true value of reliability and the unknown parameter corresponding to four different censoring proportions from the original sample.
4. Conclusions
Under type II censoring, the relative efficiencies of the proposed shrinkage estimators (relative to MLE) are shown in table 1. The shrunken estimators have been found to be better than the MLEs which are conventionally employed by practitioners for the purpose of parameter estimation, with respect to relative efficiency. The developed shrinkage estimators perform better than the usual ML estimator when the guess (or the assumed true) value of the reliability function is approximately the true value of the parameter for small sample size. It is evident that 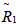 is most efficient followed by
is most efficient followed by 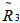 ,
, 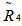 and
and  , in that order, for the entire range of Θ0. Higher parameter value gives more efficiency to all the proposed shrinkage estimators. It is observed that lesser the censoring proportion, more is the efficiency in the constructed estimators, which implies that the proposed estimators remain more precise and closer to the true parameter values even when a larger sample proportion has been truncated. Under the empirical study setup, the proposed estimators are found to be highly efficient even corresponding to a Censoring Proportion which is as low as 0.23. Thus, all the four proposed shrinkage estimators significantly improve the target reliability function in comparison with the standard MLE.
, in that order, for the entire range of Θ0. Higher parameter value gives more efficiency to all the proposed shrinkage estimators. It is observed that lesser the censoring proportion, more is the efficiency in the constructed estimators, which implies that the proposed estimators remain more precise and closer to the true parameter values even when a larger sample proportion has been truncated. Under the empirical study setup, the proposed estimators are found to be highly efficient even corresponding to a Censoring Proportion which is as low as 0.23. Thus, all the four proposed shrinkage estimators significantly improve the target reliability function in comparison with the standard MLE.Table 1. Performance under type II censoring using relative efficiency indices
 |
| |
|
References
| [1] | Baklizi, A., 2003, Shrinkage Estimation of the Exponential Reliability with censored data. Focus on Applied Statistics, Nova Science Publishers Inc. Ed. Mhd. Ahsanullah. 195-204. |
| [2] | Casella, G. and Lehmann, E., 1998, Theory of Point Estimation, Springer-Verlag. |
| [3] | Chaturvedi, A. and Singh K.G., 2006, Bayesian Estimation procedures for a Family of Lifetime Distributions under squared Error and Entropy Losses, Metron, 64,179-98. |
| [4] | Chiou, P., 1993, , Communications in Statistics- Theory and Methods, 22(5), 1483-1494. |
| [5] | Martz, H. F. and Waller, R.A., 1982, Bayesian Reliability Analysis, John Wiley Sons Inc. |
| [6] | Pandey, M., 1983, Shrinkage estimation of the Exponential scale parameter. IEEE Trans. Rel. 2, 203-5. |
| [7] | Prakash, G. and Singh, D.C., 2006, Shrinkage Testimators for the Inverse Dispersion of the Inverse Gaussian Distribution under the LINEX Loss Function, Australian Journal of Statistics, 35(4), 463-470. |
| [8] | Prakash, G. and Singh, D.C., 2008, Shrinkage Estimation in ExponentialType II Censored Data under the LINEX Loss Function, Journal of Korean Statistical Society, 37(1), 53-61. |
| [9] | Prakash, G. and Singh, D.C., 2009, A Bayesian shrinkage approach in Weibull Type-II censored data using prior point information. REVSTAT, 7(2), 171-197. |
| [10] | Singh, H. P. and Shukla, S. K., 2000, Estimation in the Two Parameter Weibull Distribution with Prior Information, IAPQR Transactions, 25(2), 107-118. |
| [11] | Thompson, J., 1968, Some Shrinkage Techniques for estimating the Mean, JASA, 63, 113-22. |
| [12] | Tse, S. and Tso, G., 1996, Shrinkage Estimation of Reliability for Exponentially Distributed Lifetimes, Comm. Stat. Simul. Comp, 25(2), 415-30. |
| [13] | Zacks, S. and Even, M., 1996, The Efficiencies in Small Samples of the Maximum Likelihood and Best Unbiased Estimators of Reliability Functions, JASA, 61, 1033-51. |

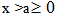 be real-valued, differentiable, strictly increasing function of x (increasing to infinity) with g(a)=0 and g’(x) stands for the derivative of g(x). We assume that the inverse function g-1 (x) of g(x) exists. The following are special cases:(i) For g(x) = x, β = 1, we obtain exponential distribution.(ii) For g(x) = x, we obtain Weibull distribution.(iii) For g(x) = log(1+xb), b>0 and β = 1,we obtain Burr distribution.(iv) For g(x) = log(x/a) and β = 1, we obtain Pareto distribution.(v) For g(x) = x, β = 2, we obtain Rayleigh distribution.The quantity we want to estimate is
be real-valued, differentiable, strictly increasing function of x (increasing to infinity) with g(a)=0 and g’(x) stands for the derivative of g(x). We assume that the inverse function g-1 (x) of g(x) exists. The following are special cases:(i) For g(x) = x, β = 1, we obtain exponential distribution.(ii) For g(x) = x, we obtain Weibull distribution.(iii) For g(x) = log(1+xb), b>0 and β = 1,we obtain Burr distribution.(iv) For g(x) = log(x/a) and β = 1, we obtain Pareto distribution.(v) For g(x) = x, β = 2, we obtain Rayleigh distribution.The quantity we want to estimate is 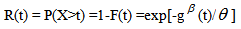 We consider a random sample of size n from this distribution such that the data is censored when a predetermined number of failures r occur: Type II censoring. In type II censoring testing is terminated at the observed time of the r th failure. The censoring time is a random variable while r is fixed.Joint pdf of
We consider a random sample of size n from this distribution such that the data is censored when a predetermined number of failures r occur: Type II censoring. In type II censoring testing is terminated at the observed time of the r th failure. The censoring time is a random variable while r is fixed.Joint pdf of  is given by
is given by Assuming β to be a known quantity, mle of
Assuming β to be a known quantity, mle of 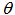 is
is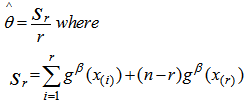
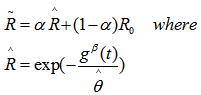
 is estimated by mle of
is estimated by mle of  ,
,  is the prior guess of the experimenter which may be based on information based on the past experience. For a specified value of
is the prior guess of the experimenter which may be based on information based on the past experience. For a specified value of  we can calculate
we can calculate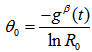
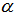 is assumed to lie between 0 and 1 inclusive, which may be determined in the following ways :
is assumed to lie between 0 and 1 inclusive, which may be determined in the following ways : is chosen such that it minimizes mean square error of
is chosen such that it minimizes mean square error of  given by
given by 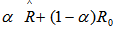 .Therefore,
.Therefore,  where
where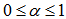
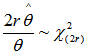 exactly. Thus, we have
exactly. Thus, we have 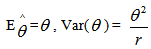
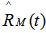 MLE of the reliability
MLE of the reliability 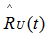 UMVUE of reliabilityWe now obtain
UMVUE of reliabilityWe now obtain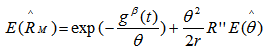
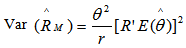
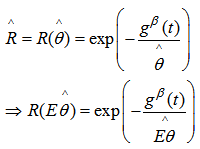
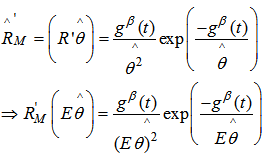
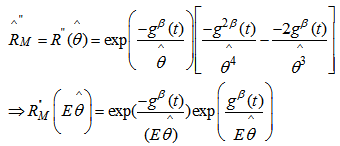
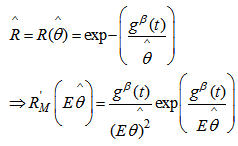
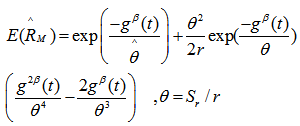
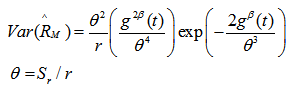
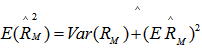
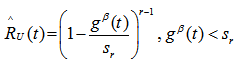
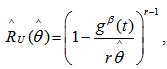
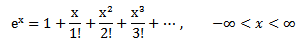
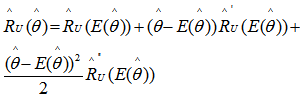
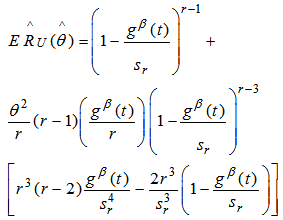

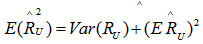
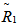 is based on MLE which is obtained by substituting
is based on MLE which is obtained by substituting 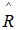 with
with  ,
, 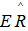 with
with  and
and 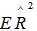 with
with 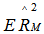 for a specified value of
for a specified value of 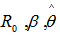 each, in expressions 2.3 and 2.5 .The second shrinkage estimator
each, in expressions 2.3 and 2.5 .The second shrinkage estimator 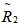 is based on UMVUE which is obtained by substituting
is based on UMVUE which is obtained by substituting  with
with  ,
, 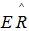 with
with 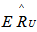 and
and  with
with 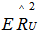 for a specified value of
for a specified value of 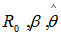 each, in expressions 2.3 and 2.5The third shrinkage estimator
each, in expressions 2.3 and 2.5The third shrinkage estimator  is based on P-value of the following test
is based on P-value of the following test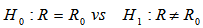
 , is assumed under H0.Let t represent the observed value of the statistic T.The P-value for this test is
, is assumed under H0.Let t represent the observed value of the statistic T.The P-value for this test is 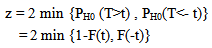
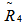 is based on the square root of the P-value of the above test such that the shrinkage estimator is obtained by replacing 1-α with the square root of the P-value of this test.
is based on the square root of the P-value of the above test such that the shrinkage estimator is obtained by replacing 1-α with the square root of the P-value of this test.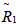 is most efficient followed by
is most efficient followed by 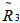 ,
, 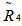 and
and  , in that order, for the entire range of Θ0. Higher parameter value gives more efficiency to all the proposed shrinkage estimators. It is observed that lesser the censoring proportion, more is the efficiency in the constructed estimators, which implies that the proposed estimators remain more precise and closer to the true parameter values even when a larger sample proportion has been truncated. Under the empirical study setup, the proposed estimators are found to be highly efficient even corresponding to a Censoring Proportion which is as low as 0.23. Thus, all the four proposed shrinkage estimators significantly improve the target reliability function in comparison with the standard MLE.
, in that order, for the entire range of Θ0. Higher parameter value gives more efficiency to all the proposed shrinkage estimators. It is observed that lesser the censoring proportion, more is the efficiency in the constructed estimators, which implies that the proposed estimators remain more precise and closer to the true parameter values even when a larger sample proportion has been truncated. Under the empirical study setup, the proposed estimators are found to be highly efficient even corresponding to a Censoring Proportion which is as low as 0.23. Thus, all the four proposed shrinkage estimators significantly improve the target reliability function in comparison with the standard MLE. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML