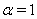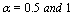-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2014; 4(3): 83-91
doi:10.5923/j.ajcam.20140403.03
A Decomposition Algorithm for the Solution of Fractional Quadratic Riccati Differential Equations with Caputo Derivatives
1Department of Mathematical Sciences, Olabisi Onabanjo University of Ago-Iwoye, P.M.B 2002, Ago-Iwoye, Ogun State, Nigeria
2Department of Mathematics, University of Ilorin, P.M.B 1515, Ilorin, Nigeria
Correspondence to: O. S. Odetunde, Department of Mathematical Sciences, Olabisi Onabanjo University of Ago-Iwoye, P.M.B 2002, Ago-Iwoye, Ogun State, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
An Iterative Decomposition Method is applied to solve Fractional Quadratic Riccati Differential Equations in which the fractional derivatives are given in the Caputo sense. The method presents solutions as rapidly convergent infinite series of easily computable terms. Solutions obtained compared favorably with exact solutions and solutions obtained by other known methods.
Keywords: Fractional Riccati Differential Equations, Caputo Derivatives, Iterative Decomposition Method
Cite this paper: O. S. Odetunde, O. A. Taiwo, A Decomposition Algorithm for the Solution of Fractional Quadratic Riccati Differential Equations with Caputo Derivatives, American Journal of Computational and Applied Mathematics , Vol. 4 No. 3, 2014, pp. 83-91. doi: 10.5923/j.ajcam.20140403.03.
Article Outline
1. Introduction
- Fractional Differential Equations, which are a generalization of differential equations have been applied to model many physical models very accurately. They have been used extensively in such areas as Thermal Engineering, acoustics, Electromagnetism, Control Theory of Dynamical Systems, Robotics, Viscoelasticity, Diffusion, Signal Processing, Population Dynamics and so on [4, 5, 13].Riccati Differential Equations are named after the Italian Nobleman Jacapo Francesco Riccati (1676-1754) [4]. In [16], the fundamental theories of the Riccati equations, and diffusion processes are discussed. The one-dimensional Schrodinger equation is closely related to a Riccati Differential Equation [15]. Solitary wave solution of a nonlinear partial differential equation can be represented as a polynomial in two elementary functions satisfying a projective Riccati differential equation [7].Riccati differential equations are known to be concerned with applications in pattern formation in dynamic games, linear systems with Markovian jumps, river flows, econometric models, stochastic systems, control theory, and diffusion problems [10, 15, 16].Many authors and researchers have studied the analytical and approximate solutions of Riccati differential equations. Some approximate solutions have been obtained from Homotopy Perturbation method (HPM) [1, 2, 3, 12], Homotopy Analysis Method (HAM) [4] and the Variational Iteration Method (VIM) [7].In this paper, we consider the fractional quadratic Riccati differential equation
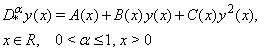 | (1) |
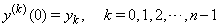 | (2) |
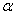 is the order of the fractional derivative,
is the order of the fractional derivative, 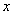 is an integer,
is an integer, 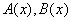 and
and 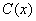 are known functions, and
are known functions, and 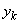 is a constant. The derivative is the Caputo-type derivatives.It is well known that most fractional differential equations do not have analytical solutions. Several authors have considered the approximate solution (1)-(2) using modifications of various methods, which have been applied successfully to integer-order differential equations. For instance, the Fractional Variational Iteration Method (FVIM) was applied in [8]. In [11], the well-known Adomian Decomposition Method (ADM) was considered for the same problems. In [12], the Homotopy Perturbation Method (HPM) was modified to solve fractional order quadratic Riccati differential equations.In [4], the HPM and ADM are compared for quadratic Riccati differential equations; and in [10], the Homotopy Analysis Method is applied to fractional Riccati equations. In [15], the Bernstein operational matrices are applied; motivated probably by the results in [5]. In [4], the Differential Transform Method (DTM) is applied.In this paper, we propose to apply the Iterative Decomposition Method (IDM) which has been applied successfully for integer-order differential equations (see [16, 17]). The success of the method for integer-order differential equations motivated [17, 18]. The method is devoid of any form of linearization or discretization.The rest of the paper is organized as follows:In section 2, we give briefly definitions related to the theory of fractional calculus. In section 3, we present the solution procedure of the Iterative Decomposition Method (IDM). Numerical examples are presented in section 4 to illustrate the efficiency and accuracy of the IDM. The conclusions are then given in the in the last section 5.
is a constant. The derivative is the Caputo-type derivatives.It is well known that most fractional differential equations do not have analytical solutions. Several authors have considered the approximate solution (1)-(2) using modifications of various methods, which have been applied successfully to integer-order differential equations. For instance, the Fractional Variational Iteration Method (FVIM) was applied in [8]. In [11], the well-known Adomian Decomposition Method (ADM) was considered for the same problems. In [12], the Homotopy Perturbation Method (HPM) was modified to solve fractional order quadratic Riccati differential equations.In [4], the HPM and ADM are compared for quadratic Riccati differential equations; and in [10], the Homotopy Analysis Method is applied to fractional Riccati equations. In [15], the Bernstein operational matrices are applied; motivated probably by the results in [5]. In [4], the Differential Transform Method (DTM) is applied.In this paper, we propose to apply the Iterative Decomposition Method (IDM) which has been applied successfully for integer-order differential equations (see [16, 17]). The success of the method for integer-order differential equations motivated [17, 18]. The method is devoid of any form of linearization or discretization.The rest of the paper is organized as follows:In section 2, we give briefly definitions related to the theory of fractional calculus. In section 3, we present the solution procedure of the Iterative Decomposition Method (IDM). Numerical examples are presented in section 4 to illustrate the efficiency and accuracy of the IDM. The conclusions are then given in the in the last section 5.2. Basic Definitions
- In this section, we give some definitions and properties of the fractional calculus.Definition 2.1:A real function
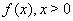 , is said to be in the space
, is said to be in the space 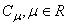 if there exists a real number
if there exists a real number 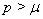 , such that
, such that  , where
, where 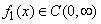 , and it is said to be in space
, and it is said to be in space 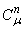 if and only if
if and only if 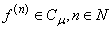 . Clearly
. Clearly 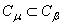 if
if  .Definition 2.2:Let
.Definition 2.2:Let 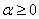 , and
, and 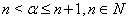 . The operator
. The operator 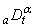 , defined by
, defined by 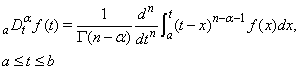 | (3) |
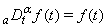 is called the Riemann-Liouville Fractional derivative operator of order
is called the Riemann-Liouville Fractional derivative operator of order 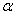 .Definition 2.3:The Riemann-Liouville fractional integral operator defined on
.Definition 2.3:The Riemann-Liouville fractional integral operator defined on 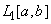 of order
of order 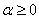 of a function
of a function 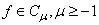 is defined as
is defined as 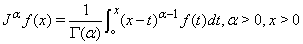 | (4) |
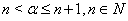 , and
, and 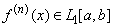 . The operator
. The operator 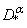 defined by
defined by 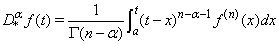 | (5) |
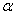 .Properties of the operator
.Properties of the operator 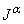 is found in [7] and include the following
is found in [7] and include the following 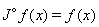 | (6) |
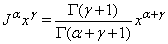 | (7) |
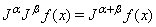 | (8) |
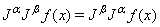 | (9) |
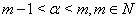 and
and  , then
, then 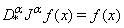 | (10) |
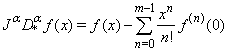 | (11) |
3. Iterative Decomposition Method
- For the fractional quadratic Riccati differential equation (1),
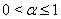 , with initial condition
, with initial condition 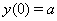 , by applying the operator
, by applying the operator 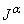 to both sides of (1), we have
to both sides of (1), we have 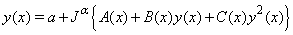 | (12) |
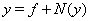 | (13) |
 | (14) |
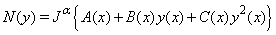 | (15) |
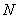 is then decomposed as
is then decomposed as  | (16) |
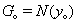
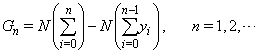 | (17) |
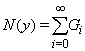 set
set 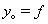 . From (13) and (14), we have
. From (13) and (14), we have  Then,
Then,  | (18) |
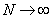 .
. 4. Numerical Examples
- We now apply the method proposed in section 3 to solve some numerical examples to establish the accuracy and efficiency of the method.Example 4.1 [19]Consider the Riccati Differential equation
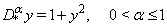 | (19) |
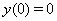 .The exact solution for the case
.The exact solution for the case 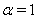 is
is 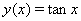 .By the Iterative Decomposition Method (IDM),
.By the Iterative Decomposition Method (IDM), 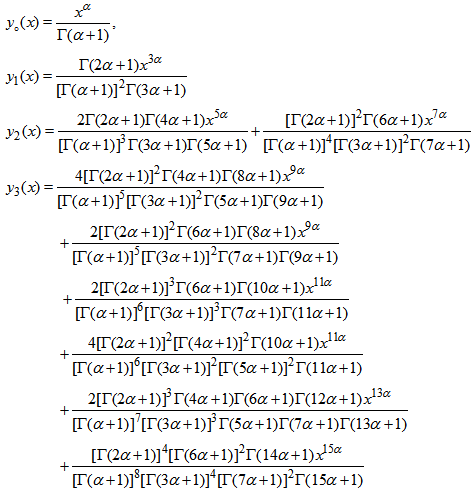 | (20) |
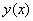 can be approximated as
can be approximated as 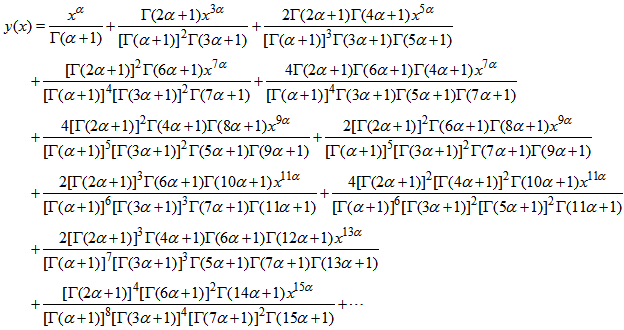 | (21) |
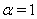 ,
, 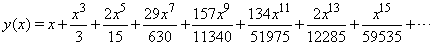 | (22) |
|
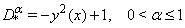 | (23) |
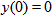 .The exact solution for the case
.The exact solution for the case 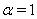 is
is 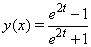 . Applying the inverse operator to both sides of (23),
. Applying the inverse operator to both sides of (23), 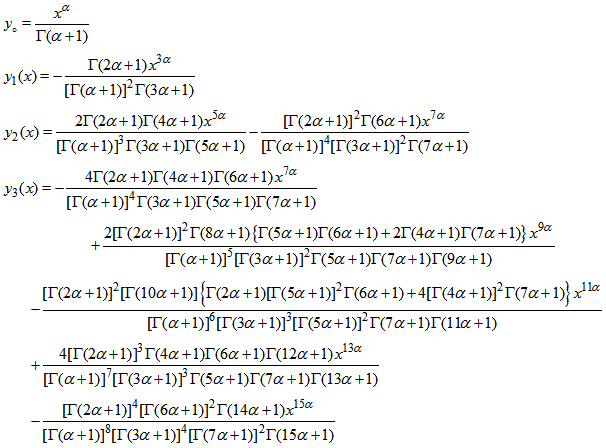 | (24) |
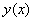 can be approximated as
can be approximated as 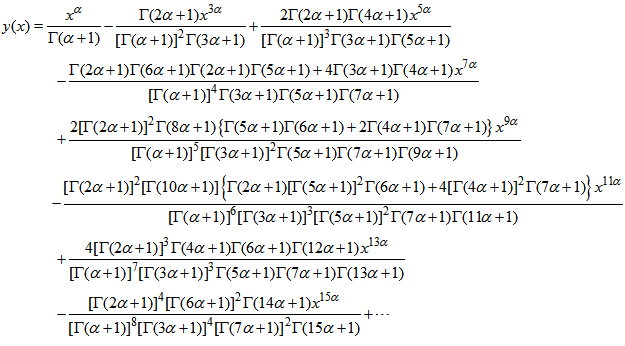 | (25) |
|
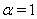 ,
, 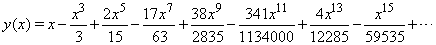 | (26) |
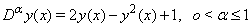 | (27) |
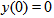 The exact solution for the case
The exact solution for the case 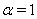 is
is 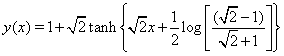 Applying the inverse operator to both sides of (27) and using the initial condition given
Applying the inverse operator to both sides of (27) and using the initial condition given 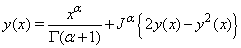 Taking
Taking 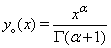 , by the IDM, we have
, by the IDM, we have 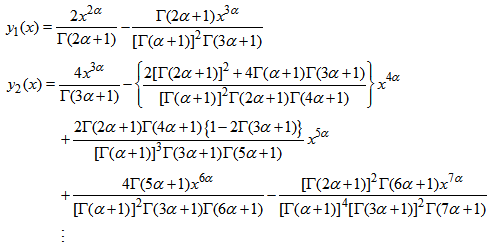 | (28) |
 can be approximated as
can be approximated as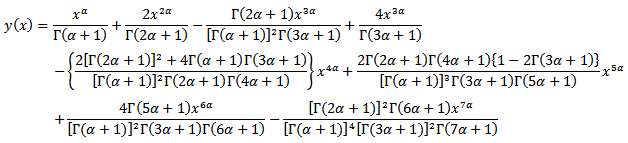 For the particular case
For the particular case 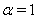 , we have
, we have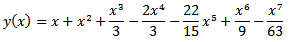
|
 | (29) |
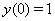 The exact solution for the case
The exact solution for the case 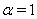 is
is  Applying the inverse operator to both sides of (29),
Applying the inverse operator to both sides of (29), 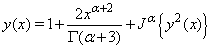 | (30) |
 we have
we have 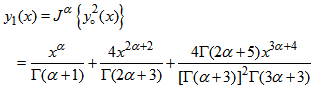 | (31) |
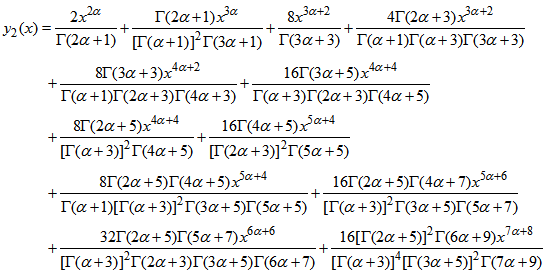 | (32) |
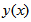 can be approximated as
can be approximated as  For the particular case
For the particular case 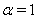 ,
, 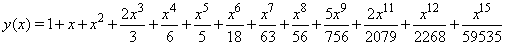
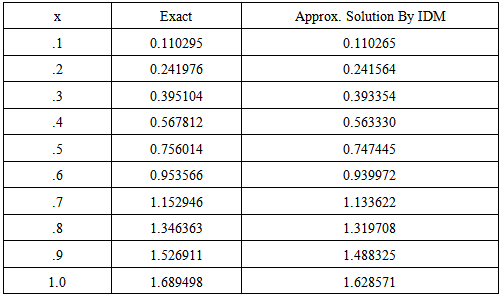
5. Conclusions
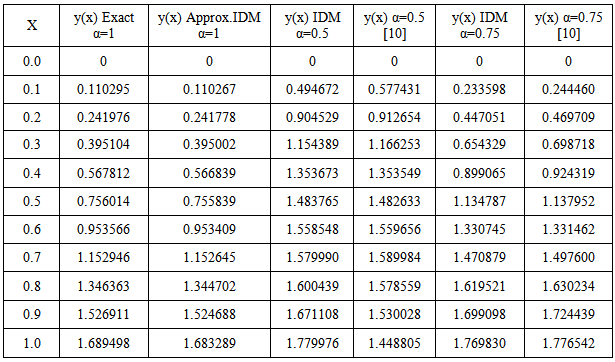
- In this paper, the Iteration Decomposition Method has been successfully applied to find approximate solutions of fractional quadratic Riccati Differential Equations.The IDM is effective for Riccati differential equations, and hold very great promise for its applicability to other nonlinear fractional differential equations. The four examples used indicate the efficiency and accuracy of the method for fractional quadratic Riccati differential equations. The results obtained are in very acceptable agreement with those obtained by other known methods.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML